[manual]Calculator
| Associativity | /prior2omitted* | 条件設定に依らない括弧明示 | Answer |
|---|---|---|---|
| 下記4種類 | e^(-i(1pi()2/2i(5-3-1)i/(-4))) | =e^(i{t}) | |
| left | false | e^(-i(1pi(){2/{2i({5-3}-1)i}}/(-4))) | =e^(i{-pi/4}) |
| right | false | e^(-i({1pi()2}/{{2i(5-{3-1})i}/(-4)})) | =e^(i{-4pi/3}) |
| left | true | e^(-i(1pi(){2/2i}({5-3}-1){i/(-4)})) | =e^(i{pi/4}) |
| right | true | e^(-i(1pi(){2/2i}(5-{3-1}){i/(-4)})) | =e^(i{3pi/4}) |
| 実数演算不可(0*Infinity->NaN発生) | |||
| 項目 | 内容 |
|---|---|
|
目次
test case |
・incircle:面積のanalogyの実施例(円周率の基準径の幾何学)
・sigmoid:sigmoid曲線(zeta関数のみ、非対称性あり) ・fraction:連分数展開(Machine epsilonの精度保証) ・golden-triangle||-gnomon:黄金比の三角形(5回の回転対称性)とtruss構造 ・Kahaner:integralの相対誤差(参考Docsの抜粋+α) ⇒区間分割数:NI増で解析解に漸近 ⇒適用の目安 ・有界の任意関数(周期関数を含む):adaptive-stepの時間発展 ⇒ _o45() ・端点の特異性あり(極を含む):DE求積法 ⇒ _i0() ・低次の多項式:合成Simpson公式 ⇒ _i4() ・折れ線graph:台形公式 ⇒ _i2() ・Fourier:周期関数f(x)の複素Fourier多項式(Ver.2.809.131以降、omega導入のFourierN参照) ・mod:N進法の線形結合(inv_mod用) ・N-ary:'rsum'の厳密な再帰計算と導出式の比較 ・Seki-Aitken:Seki-AitkenのΔ2乗加速法 Ver.2.738.107以降、snが単調変化の前提で多重加速tn(tn(sn))を追加 ⇒tn多重化の対策:snの名前衝突回避tn(=<sn_,n)=<f(sn_)||単独scope化tn(=<sn,n)=<last[,f(sn)] ⇒4重加速の結果:n=[0,2*4]のsnの約4.6桁⇒tn(tn(tn(tn(sn,n))))の約16桁(手計算量sn9点⇒tn7+5+3+1点) ⇒Sekiの結果:n=[15,17]のsnの約10桁⇒tn(sn,n-2)の16桁以上(手計算量sn14点⇒tn1点) -zeta~-2-err:収束速さがlogの級数の場合、効果が低い ⇒ 同上の漸化式len(2n)=f(len(n))を仮定 -zeta-3~-4-err:-absで得られるζ関数の非自明な零点(有効数字7桁程度) ⇒2重加速の結果:snの約1桁⇒tn(tn(sn))の限界7桁(定義域の内外⇒解析接続の一意性) ・Seki-Bernoulli:Seki-Bernoulli数 ・Faulhaber:べき乗和をSeki-Bernoulli数の多項式で記述 ・Apéry:Apéryの定数 ⇔ 無理数のζ(3) 3重積分:Ver.2.806.130以降、DE求積法(端点の特異性あり) ・residue:複素線積分の留数定理(反時計回りの周回積分経路Cを正多角形で記述) -gamma||-ac:gamma関数に適用 ⇒DE求積法の分割数||無限乗積の打切り次数:NI||n0増で厳密解に漸近 -1/zeta:zeta関数の逆数に適用 ・arg:Cauchyの偏角の原理(有理型関数の零点と極の個数の差に対応) -gamma:gamma関数に適用 ⇒原点と負の整数に特異点(1位の極)が存在 ・dlog:対数微分 ⇒偏角の原理に右辺を採用:(log(f(z))'=f'(z)/f(z) ・Bessel:定義域real(x)>0のBessel関数(Ver.2.821.132以降、拡充) -_t45:時間反転対称性のBessel関数(adaptive-stepの時間発展) -gamma:複素数のBessel関数 ・Airy:実数のAiry関数 -_t45||-z:複素数のAiry関数(Ver.2.821.133以降、積分表示 ⇒ adaptive-stepの時間発展) ・heat:同方向@kd<0の解析接続の可視化(0~12段階の温度分布) -2:異方向@kd>0の解析接続の可視化(同上) ・Collatz~Goldbach:数学上の未解決問題(Number変換参照) Collatz~quality~-L:Collatz予想 pi_(x)~Goldbach:Goldbach予想 ・pi_(x):素数計数関数と近似式の比較 o(x):近似式の誤差項 Ver.2.704.98以降、O(x) ⇒ o(x)(Order表記との重複を解消) -real:x=[10,10**28]で実際の誤差との比較 ⇒べき指数:Riemann予想の1/2に近い ・Mertens:Ver.2.703.98以降、Mertens予想 ・Fermat:Ver.2.728.103以降、Fermatの最終定理のWiles証明(西暦1995年) -n=3~19:n≧3で整数の格子点と一致の解なし(abc予想のqualityがnの上限の存在を示唆) -little:Fermatの小定理(inv_mod用) ・Frey-Hellegouarch:Frey-Hellegouarch曲線y**2=x(x-a)(x+b) Szpiro:互いに素でa+b=cと以下を満たす曲線のquality ⇒判別式:D=16*(a*b*c)**2 ⇒極小判別式:Ver.2.851.156以降、Dmin=(a*b*c/2)**2(参考DocsのSzpiro予想) ⇒導手:N=rad(a*b*c/16) ・Weierstrass-form:Weierstrass標準形の楕円曲線y**2=x**3+a*x+b ・elliptic:非特異な楕円曲線(nodeとcuspを除く) -add:加法(傾きkを条件分岐の最短表記) ⇒2点間の傾き:k=(y2-y1)/(x2-x1) ⇒接線の傾き:2y*y'=3x**2+a ⇒ y'=(3x**2+a)/(2y) ⇒傾きの共通化(有限体を除く):k=(x1**2+x1*x2+x2**2+a)/(y1+y2) ⇒交点Rの係数比較:x**3-(k*x+c)**2+a*x+b=(x-x1)(x-x2)(x-x3) ⇒ -k**2=-(x1+x2)-x3 ⇒y3の符号反転(群の生成):k=(-y3-y1)/(x3-x1) ⇔ P+Q=-R, P+Q+R=O ⇒逆元:R+(-R)=O(無限遠点の場合、x軸で線対称) -O:加法の単位元||零元(無限遠点) Ver.2.728.104以降、零元の座標定義を修正(b=0の要素(0,0)と区別が必須) ⇒零元の座標定義(実数体):(false,false) -scalar:scalar倍算 -p:mod pで還元の有限体が作る巡回群の基点Gの基点候補(素数pの法で離散化) Ver.2.724.103以降、一部訂正:基点 ⇒ 基点候補 Ver.2.725.103以降、y=p/2の線対称性の基点候補を追加 ⇒離散対数問題(P≠NPの前提):GとQ=d*Gの2点から離散対数dの逆算は困難(一方向性||非対称性) -aff:Ver.2.728.104以降、isValidの全探索から同上の全affine点をplot Ver.2.730.104以降、探索の基点候補を全affine点に変更 ⇒対称性の保存:y=p/2の線対称性のpairで全経路履歴を明示 -Np:Ver.2.747.111以降、全affine点の個数+1(零元を含む全要素数) Ver.2.847.154以降、修正 -ap:Ver.2.847.154以降、ap:=p+1-Np(次のbad還元を除く、good還元の素数用) -Fp:LMFDB定義のFp(T):=1+k1*T+k2*p*T**2, T=p**(-s) ⇒ Euler積表示のL(s):=素数pのΠ1/Fp(T) ⇒乗法的関数:weight=2のcusp形式(modularity定理) ⇒1次の係数k1:加法的還元の場合、false Ver.2.757.115~2.847.154以降、訂正 ⇒2次の係数k2:乗法的還元の場合、false Ver.2.757.115~2.847.154以降、訂正 -an:Ver.2.849.156以降、L-functionのDirichlet級数の係数an(同上のk1=-apとk2から換算) ⇒未最適化:全探索のeval_Npと素因数分解 ⇒an導出のdouble-check:Gemini 2.5世代 ⇒LMFDBのdouble-check:Sage Cell Server ⇒ n=101; EllipticCurve([-1, 1]).an(n) -> 2 -BSD:同上のNpをlookup-table化(線形時間でBSD予想のrankを評価) -je*4:Ver.2.753.113以降、pのN数を増点(約4倍) ⇒a=-1,b=7:rank=1が不明確 -L:同上のHasse-WeilのL関数(Euler積)を複素数平面にplot Ver.2.755.114以降、real(s)≤3/2の場合、絶対収束の範囲外で不正確 ⇒analytic rank:LMFDBのL-functionのZ(臨界線)-plot参照(Dirichlet級数と関数等式で記述) ⇒BSD予想:s=1の零点の位数=rankの階数>0を明示(厳密なplot点のzeros参照) -je*4:Ver.2.753.113以降、pのN数増で零点に接近を確認 -Aitken:Ver.2.854.158以降、Δ2乗加速法を適用(N=2**nを仮定) ⇒解析接続の一意性:臨界領域の場合、零点の精度改善(ζ関数同様) -an:Ver.2.853.158以降、同上のdouble-check(N=101のDirichlet級数) zeros:Ver.2.718.101以降、重複度の異なる正則関数を複素数平面にplot ⇒1位の孤立零点:後述のξ関数相当の完備関数(臨界線⇒対称軸に完備化)の関数形を明示 -G:O起点の巡回群要素Q=d*G=O+G+G+G+... Ver.2.728.104以降、零元の座標定義と到達判定の致命的な不具合(巡回しない原因)を修正 零元の座標定義(有限体):(0,0) ⇒ (false, 零元の到達判定(実数体⇒有限体):isO=(x1===x2)&&(y1===-y2) ⇒ (y1===p-y2) Ver.2.731.104以降、次のinv内の判定を統合:(y1===p-y2) ⇒ (y1===p-y2||y1===0) 最適化とdouble-check:式変数isValid ⇒倍精度の目安(除法の制約):p<20 ⇒Ver.2.728.104以降、6位の基点:(6,1)||(8,3) -G-bp:Ver.2.727.103以降、同上の基点のみをd=[1,2p+1]で表示(Ver.2.728.104以降、巡回を確認) -G-2:O起点の巡回群要素Q=d*G=O+G+G+G+... ⇒全経路履歴の分布:y=p/2の線対称性を明示 ⇒p=17の場合、桁数不足 Ver.2.726.103以降、式変数inv_modで桁数不足を対策(p進法で1*v*v*...のmod pを演算) ⇒Ver.2.728.104以降、18位の基点:(10,2)||(15,4) -G-2-bp:Ver.2.727.103以降、同上の基点のみをd=[1,2p+1]で表示(Ver.2.728.104以降、巡回を確認) -G-3:O起点の巡回群要素Q=d*G=O+G+G+G+... ⇒Ver.2.728.104以降、20位の基点:(4,4)||(8,1) -G-3-bp:Ver.2.727.103以降、同上の基点のみをd=[1,2p+1]で表示(Ver.2.728.104以降、巡回を確認) =G+:G起点の巡回群要素Q=d*G=G+G+G+... ⇒O+G+G+G+...=G+G+G+... -G-4:Ver.2.726.103以降、桁数不足を対策して追加 ⇒Ver.2.728.104以降、12位の基点:(8,4)||(17,4)||(28,5)||(33,6) -G-4-bp:Ver.2.727.103以降、同上の基点のみをd=[1,2p+1]で表示(Ver.2.728.104以降、巡回を確認) -G-5~-9:Ver.2.730.104以降、以上の不具合を修正後に追加 ・Eisenstein:Eisenstein級数を複素数平面にplot ⇒総和順序の仮定:低次の項から昇順(絶対収束の場合、可換) -ra:real analytic Eisenstein級数を複素数平面にplot(s=1の極を除く) ⇒複素数の複素数乗で成立:1/z**s ⇔ z**(-s) ・Dedekind: Dedekindのeta関数を複素数平面にplot ・Ramanujan:RamanujanのDelta関数を複素数平面にplot -tau:Ramanujanのτ数(参考論文[3]) ⇒τ(1):演算都合上、約数関数σ(0):=0 ・zeta:定義域real(s)>1のζ関数を複素数平面にplot(s=1の極を除く) Ver.2.682.98以降、解析接続を追加 Ver.2.703.98以降、Möbius関数を追加 ・zeta-ac:Riemann zeta関数の解析接続(Dirichlet級数と関数等式で記述) ・eta-ac:Dirichlet eta関数の解析接続(Riemann zeta関数で記述) -zero:Ver.2.695.98以降、η関数の非自明な零点(ζ関数に一致)の探索用に追加 -z:同上のη関数を複素数平面にplot ・completed:Ver.2.718.101以降、完備関数を一般化して複素数平面にplot ⇒完備関数(符号なし):f(x)+i*g(x,k) ⇒f(x)の次数:2(符号の変曲点近傍を除く) ⇒g(x,k)の次数:3(k>0.5でopen、k>>1で線形近似) ⇒Ver.2.734.104~2.747.113以降、以上の完備関数に対応する楕円曲線の -ex:Ver.2.720.101以降、同上の完備関数のplot範囲を拡張(相似形を確認) ・Riemann:Riemann予想の非自明な零点の計算結果(ζ関数の実部と虚部をplot) -z:同上のζ関数を複素数平面にplot ⇒Dirichlet級数の定義域:real(s)>-1に拡張で精度改善(関数等式の境界に対する精度保証) ⇒関数等式の境界:real(s)=0(後述の境界線real(s)=1の両側の数値的な連続性を優先) -obvious:Riemann予想の自明な零点の計算結果(負の偶数が零点は関数等式から自明) -zero:Ver.2.694.98以降、ζ関数の非自明な零点の探索用に追加 ⇒無限乗積||級数の打切り次数:n∝abs(s-1/2)(後述のξ関数の場合、ζ関数より1桁増) -z:同上のζ関数を複素数平面にplot -EM:Ver.2.700.98以降、Euler-Maclaurinの和公式で得られるζ関数と比較 Ver.2.703.98以降、比較対象を追加(η関数の等価関係とHasseの2重級数) Ver.2.802.128以降、比較対象を追加(Knopp-HasseのEulerの和公式の2重級数) Ver.2.802.128以降、打切り次数n1=50 ⇒ n0(横並び) ⇒以上の全公式を式変数に変換のため、非常に重い -EM-2:Ver.2.802.128以降、大域収束性のζ関数のdouble-check 以降、追加の計算結果(Euler-Maclaurinの和公式で最適化のζ関数) -abs:同上のSeki-Bernoulli数をlookup-table化(ζ関数の絶対値をplot) ⇒t=[0,600]の零点の個数≒29+50+59+64+68+72(6等分割の目算) ⇒Ver.2.708.100以降、tableを最適化:Bn(n) ⇒ Bn(n)/n! -x=1:同上の臨界線real(s)=1/2と境界線real(s)=1の比較 ⇒abs(ζ(境界線))>0 ⇒極大点の位置に強い相関あり(次のξ関数に完備化して議論) -xi:Ver.2.701.98以降、Euler-Maclaurinの和公式で得られるξ関数の計算結果(ξ関数のreal成分をplot) ⇒後述のξ関数と零点の位置がほぼ一致(nの違いを含めて縦軸の差異は1桁程度の相似形) ⇒Ver.2.694.98以降、解析接続の一意性をdouble-check -f(x):Ver.2.706.99以降、同上の臨界領域x方向のξ関数の計算結果(各real(ξ(s))=0の近傍) ⇒任意tの偶関数:f(x):=real(ξ(x+i*t)), f'(1/2)=0 ⇒ f≠h, h(x)=0 -z:同上のξ関数を複素数平面にplot -g(x):Ver.2.711.100以降、同上の臨界領域x方向のξ関数の計算結果(各imag(ξ(s))=0の近傍) ⇒任意tの奇関数:g(x):=imag(ξ(x+i*t)), g(1/2)=0 ⇒ g≠h, h(x)=0 -z:同上のξ関数を複素数平面にplot ⇒完備化の意義:ξ(1/2+i*t)=0近傍でopen ⇔ df(1/2)/dt=0近傍でclosed -ex:Ver.2.720.101以降、同上のξ関数のplot範囲を拡張(粗分割で相似形を確認) -p:f(1/2)の極大点~零点~f(1/2)の極小点のξ関数を複素数平面にplot ⇒変化の傾向:f(1/2)の曲率の変曲点≠零点≠closedの交点 ⇒stringの自己交差の向き:右~変曲点~零点~左(常に外向き) ⇒f(x)の次数:2 ⇒ 4(変曲点近傍のみ) ⇒Ver.2.711.100以降、解析接続の一意性をtriple-check 以降、当初の計算結果(Dirichlet級数の定義域で記述のζ関数) -x:ζ関数の臨界領域x方向の単調性 ⇔ 関数等式 ⇒零点の個数:解析接続で最小化(対称性の2点⇒中点の1点) -n:real(s)>-1のζ関数の計算結果(n=1e3⇒3e4) ⇒無限乗積||級数の打切り次数:n増で関数等式の境界の精度改善 -ave~-2:ζ関数の臨界領域両境界線の算術平均値と臨界線の比較 ⇒強い相関あり -diff~-2:ζ関数の臨界領域両境界線と臨界線の差分の比較 ⇒臨界線のζ(s)=0の個数∝境界線のreal(ζ(s))の変曲点の個数 -sym~-6:元の定義域と解析接続の臨界領域でζ関数の対称性の計算結果 -xi:Ver.2.692.98以降、Riemann xi関数の解析接続(Landauのξ関数で記述) ⇒s=1/2に対する4点の対称性 -x~-7:ξ関数の臨界領域x方向の単調性 ⇔ 関数等式 Ver.2.705.99以降、訂正 ⇒real成分:両軸の線対称性 ⇔ real(ξ(s))∝(x-1/2)**2 ⇔ Robin条件の拡散方程式の定常解 ⇒imag成分:imag(ξ(臨界線))=0 ⇔ imag(ξ(s))∝|x-1/2|**r(零点近傍のr≒1)||sigmoid(x-1/2) -3:ξ関数の非自明な零点を明示 -3-z:同上のξ関数を複素数平面にplot(臨界線の零点近傍@y=21.022でopen) Ver.2.706.100以降、零点の誤用を訂正 Ver.2.711.100以降、極値点の定義を追記:df(1/2)/dt=0 -7:Ver.2.691.98以降、複数個のimag(ξ(s))=0を明示(gamma関数を微修正) -7-z:同上のξ関数を複素数平面にplot(f(1/2)の極大点近傍@y=144でclosed) -7':Ver.2.694.98以降、複数個のimag(ξ(s))=0を明示(f(1/2)の極大点近傍を追加) -7'-z:同上のξ関数を複素数平面にplot(f(1/2)の極大点近傍@y=144.04でclosed) -7":Ver.2.694.98以降、零点近傍でimag成分のr≒1を明示 -7"-z:同上のξ関数を複素数平面にplot(臨界線の零点近傍@y=143.11でopen) -8:Ver.2.694.98以降、複数個のimag(ξ(s))=0を明示(f(1/2)の極小点近傍を追加) -8-z:同上のξ関数を複素数平面にplot(f(1/2)の極小点近傍@y=146.5でclosed) -9:Ver.2.694.98以降、複数個のimag(ξ(s))=0を明示(f(1/2)の極小点近傍を追加) -9-z:同上のξ関数を複素数平面にplot(f(1/2)の極小点近傍@y=447でclosed) -9":Ver.2.694.98以降、零点近傍でimag成分のr≒1を明示 -9"-z:同上のξ関数を複素数平面にplot(臨界線の零点近傍@y=446.87でopen) -zero:ξ関数の非自明な零点の計算結果(整合性の最終確認) ⇒imag成分:imag(ξ(臨界線))=0 -z:同上のξ関数を複素数平面にplot -7:Ver.2.694.98以降、f(1/2)の極大点近傍@y=144を明示 -7-x=1:境界線real(s)=1に対する解析接続の一意性を明示 Ver.2.711.100以降、訂正 ⇒境界線real(s)=1のimag(ξ(s))=0 ⇔ f(1/2)の極値点近傍 ⇒ 零点近傍でopen -8:Ver.2.694.98以降、f(1/2)の極小点近傍@y=146.5を明示 -8-x=1:境界線real(s)=1に対する解析接続の一意性を明示 ⇒境界線real(s)=1のimag(ξ(s))=0 ⇔ f(1/2)の極値点近傍 ⇒ 零点近傍でopen -9:Ver.2.694.98以降、f(1/2)の極小点近傍@y=447を明示 -9-x=1:境界線real(s)=1に対する解析接続の一意性を明示 Ver.2.843.148以降、追記して修正 ⇒境界線real(s)=1のreal(ξ(s))=0の個数 ⇔ 臨界線real(s)=1/2のξ(s)=0の個数(集合の濃度が同等) -y:ξ関数の臨界線y方向の計算結果(粗分割の傾向確認) ⇒real成分:|y|増で桁数が指数関数的な減少傾向(x方向の定常解より変化の次数大) ・beta-ac:beta関数の解析接続(gamma関数で記述) ・gamma-ac:gamma関数の解析接続(Eulerの無限乗積 Ver.2.805.130~2.806.130以降、DE求積法を追加 -inf:Ver.2.691.98以降、n**z ⇒ (n+1)**z ・digamma~-psi:gamma関数の対数微分のdigamma||psi関数(微分高階関数の数値解と解析解の比較) ・Nukiyama-Tanasawa:一般化gamma分布の特殊なNukiyama-Tanasawa分布 fV:体積基準(d32/dの正規化) fN:個数基準(d32/dの正規化) d:特性粒径(粒径≧dの体積割合が1/e≒36.8[%]) d32:Sauter平均粒径(表面積重視) d43:DeBrouckere平均粒径(体積重視) ・Rosin-Rammler:Weibull分布の特殊なRosin-Rammler分布(体積基準) fV:体積基準(d32/dの正規化) fN:球形の個数換算(d32/dの未正規化) d32:d32/d=Γ(1+3/均等数)/Γ(1+2/均等数)∝個数分布の3次/2次moment d43:d43/d=Γ(1+4/均等数)/Γ(1+3/均等数)∝個数分布の4次/3次moment -d32_old:d32_old/d=Γ(1+0/均等数)/Γ(1+(-1)/均等数)∝球形の体積/表面積(参考論文[4]) ・power-law:べき乗則(自然のfractal) d:粒径 α:べき指数 個数基準の数密度:fN∝d**α ⇒ log(fN)∝log(d) 最小粒径:dmin(物理的な個数が有限) 代表粒径:d32(散乱||揮発現象の表面積重視) ・Planck:Planckの法則の分光放射輝度(波長) -frequency:分光放射輝度(周波数) ⇒量子仮説:ε=h*ν ⇒ E(ε):=ε×整数 ⇒ Eall(s):=∫dε{f(ε)×E(ε)^(s-1)}(以下のenergy分布f(ε)参照) ・BEC:Ver.2.806.130以降、Bose-Einstein凝縮の比熱(参考Docsの例題) ⇒Newton法:反復回数20回以内で約10桁の一致(t=1.5の場合、1.710344202...) ⇒DE求積法:Bose-Einstein積分のζ(s,α):=∫f(s,α)dx/Γ(s)(定義域real(s)>1で積分表示のζ関数にαを導入) ・Bose-Einstein:Bose-Einstein分布 ⇒ Eall(s)∝ζ(s)Γ(s)(前述のzeta関数×gamma関数) ・Fermi-Dirac:Fermi-Dirac分布 ⇒ Eall(s)∝η(s)Γ(s)(前述のeta関数×gamma関数) ・rand_Pinv:確率分布に従う乱数生成の実施例 ・Newton-Raphson:Newton法の実施例 ⇒既定の収束判定条件:normc(dx)<Machine epsilon ⇒数値解のnorm:log10(normc(f))∝log10(Machine epsilon)/重複度 -3:重根の対策(現状、遭遇頻度少のため、初期値x0と差分刻みhを含む外部設定値を個別に調整) ・ODE-solver:mass-spring-damper system x:位置 v:速度 m:mass k:spring係数 c:damper係数 F:外力 ⇒以降、頻出の運動方程式の一般化(Stokesの抵抗則):x'=v, v'=(F-k*x-c*v)/m -stiff:硬い方程式(時間刻みの要調整) -PID||-out:systemの操作量uを仮定のPID制御(model-basedのdouble-check) ⇒実際にはLPF等のnoise対策あり(主に微分項) ・pendulum:Ver.2.733.104以降、理想状態の2重振り子(単振り子) ⇒初期値鋭敏性:chaosの場合、数値誤差程度の違いで時間経過の描像に大差あり -_t-t||-w:単振り子(腕先端の質点系)の角度||角速度 -physical-_t-t||-w:物理振り子(腕中間の質点系)の角度||角速度 ・galaxy-rotation-problem:Ver.2.870.162以降、銀河の回転曲線問題 ⇒標準解釈:全体で中和する電磁気力より密度波の揺らぎを含む重力が支配的 ⇔ 円軌道を仮定 ⇒可視物質baryonの古典論:回転速さv(r)∝√(質量M(r)/半径r) ⇒外縁部の観測結果:古典論より回転速さの減速が小さい(一定に近い) ⇒曲線導出のdouble-check:Gemini 2.5世代 -r_bulge*2:r_bulgeのparametric study ・3body:Ver.2.732.104以降、複素数平面に表示の平面3体問題 ⇒前提:無衝突系の時間刻み一定で重力の分母が有限の補正操作あり ⇒ |2点間距離|>r_epsを仮定 -m1-r_eps:同上の質点m1=7のr_eps依存性(時間刻み一定で連続性を比較) ⇒補正率の条件:r_eps/dr<<1(物理的根拠は未考慮) -3~5body-dt:同上の質点m1=7のdt依存性 ⇒近距離の再現性:向上の場合、距離に応じて時間刻みを可変 -3~5body-sym:2次元平面の対称解@r_eps=0(補正操作なし) ⇒共通重心:質点の有無で対称性をdouble-check ⇒徐々に数値誤差が蓄積して計算が破綻(周回数に依存) -5body-sym-1r||2r:r_eps>0の場合、近点移動成分が発生(補正率r_eps/drに依存) ⇒3次元の一般3体問題:未知変数の個数>保存則の個数(対称解以外の解析不能) -4~5body:4体以降、手動で項を追加(主に高階関数の引数の制約) -5body-_t5||_t2:時間発展の分岐を比較 -5body-_t1||_t3:Ver.2.775.121以降、追加 -5body-_t12||-_t23||-_t45:Ver.2.774.119以降、adaptive-step solverを追加 -N=5~=13:Ver.2.736.107以降、任意個数のN体simulation(強連成の方程式と一意対応の最短表記) ・orbit-kdrm=0.36:地球と月の軌道計算結果(近地点移動周期に相対位置の初期値を適合) 初期値の仮定:月の面積速度vAmを保存のため、周方向成分一部の力を消去(不確定性の背反を排除) ・Kepler:公転軌道の実施例 ・baseball:野球の実施例 ・circuit:「369の法則」の実施例(三相交流) ・switching~-load:電気回路の実施例(昇圧用のswitching回路) ・seriRLC||paraRLC-reso:共振の実施例(電波受信用の共振回路) ・EIS:EIS simulationの実施例 ・cell0d:0D-cell simplified modellingの実施例([spec]Electrochemical 0D-cell参照) ・Paris-span:未来予測の倍数と時定数を除く、西暦4000年の根拠(単純平均の概算で経過時間の約20倍) ・CO2:二酸化炭素と地球史の実施例(Younger Dryas期を基準にMilankovitch cycleを逆のこぎり波で記述) ・sea:0D-sea-level simplified modelling||陰||陽解法の実施例(気候変動の海面上昇を1次遅れ系で記述) 実測1点の最悪想定:寄与度換算で融解量を過大評価(rate換算の場合、krate1で基準年のrateを調整) 寄与度の予想:Order(100年)の時定数で西暦2039年以降に融解量が熱膨張量を逆転(徐々に顕現) Tc=900:同上の回帰直線で最終氷期⇒間氷期の海面上昇のdouble-check(温度上昇rate一定を仮定) ⇒氷期の形状因子bが10.5倍:定量性はないが、b=1に適合の場合、未来のlevelを過小評価の可能性あり -mod:modelling詳細化の実施例(Tc0を導入) ・heat0d~Toba:0D-heat simplified modelling||陰解法の実施例(気候変動の平均気温の変化量||平均気温) ・heat1d~-2.9B:heat1d_evolutionの実施例(地表の平均気温||全球凍結) 初期値の仮定:界面温度T0/T1等の値を現在基準値で固定(時間軸を移動の場合、不正確) ・Friedmann:物質優勢期を想定のFriedmann方程式@P=0のparametric study(参考論文[2]) -k=0:時空の制約条件からk=0を想定 ⇒現宇宙@q=-0.64:後期加速膨張の発散系 -dR/dt:最初期の発散と後期の減速⇒加速の変曲点(約138/2=69億年前)を明示 ⇒補足:adaptive-stepの時間発展の場合、発散直前に停止 -quality:現宇宙の系のqualityの概算(観測可能範囲) ・Schrödinger3d:Ver.2.829.139以降、同下の2次元Schrödinger方程式を3次元化(10×10分割 ⇒ 4×4×4分割) ⇒毎step高速化の検討候補:未知変数vectorの入出力の並列化(memoryと通信の同期を含むoverhead次第) -y||-z:z方向=y方向=x方向分布の対称性を確認 ・Schrödinger2d:Ver.2.826.139以降、同下の1次元Schrödinger方程式を2次元化(100分割 ⇒ 10×10分割) ⇒解像度不足:中心差分法の精度次数による計算結果の差が顕著 2次元化の仮定:等間隔の等分割(有限差分の係数krと演算子Lpを共通化) 3次元化の補足:reshapez参照 potential energyの仮定:各方向のcenterに対する偶関数 -y:y方向=x方向分布の対称性を確認 ⇒各方向の分布:centerに対する対称性を確認 -side:各方向の両端でside1=side2の結果を確認 ・Schrödinger1d:1次元Schrödinger方程式のadaptive-stepの時間発展(波動関数ψの時間と空間を強連成) Ver.2.875.167以降、訂正:波動関数の収縮(collapse) ⇒ 動的局在化(localization) 空間Δ演算子の離散化:中心差分法(境界条件を含むarea参照と拡張行列演算で記述) ⇒補足:強連成の式が単体の場合、行列演算が不要で次元拡張が容易(演算cost最小の最短表記) 初期値の仮定(正規化の操作なし):ψ0(x)=V(x) potential energyの仮定:V(x)=任意の連続関数f(x)+V0(定常状態のenergy固有値Enと関係) 境界条件の仮定:ψ"(x)=0相当の線形外挿(部分空間の確率として、成行きflux∝ψ'(x)≠0を許容) ⇒補足:ψ"'(x)=0相当の場合、発散を許容 -abs:波動関数ψを確率振幅として確率分布|ψ(x)|^2の干渉縞を明示 ⇒安定性:V(x)のpotential極小点近傍 ⇒ |ψ(x)|^2>0 -Gauss-abs:Ver.2.804.130以降、Gauss波束の確率分布|ψ(x)|^2(大域的な確率保存則を確認) -V=0:V(x)=0の波動関数ψ0(x)∝sin(k*x)*W(x)の拡散と反射過程を明示 -dx/2:同上の差分刻みdx依存性を確認 -Gauss:Ver.2.804.129以降、複素数に拡張のGauss波束(符号で進行方向が変化) -tunnel:Ver.2.804.129以降、自由粒子のtunnel効果 ⇒impulse関数:有限高さV0のpotential障壁を中央に設置 -step/8:Ver.2.831.140以降、step関数を追加 ⇒step関数:有限高さV0/8のpotential障壁を右側に設置 ⇒|ψ(x)|^2(反射と透過の分配):V0→∞で全反射 -periodic:Ver.2.790.124以降、周期境界条件を適用 ⇒V(x)の虚数の有無(exp||cos):動的局在化の程度に影響 -V(x,t):Ver.2.790.124以降、時間依存のpotentialを適用 ⇒V(x,t)の虚数の有無(exp||cos):動的局在化の程度に影響(以下、同じ解釈) ⇒位相変化の周波数応答fV→0:対称性の乱れ ⇒ 動的局在化(初期状態ψ0に依存しない) -fV=-1 -> breaking:対称性の破れの遷移状態 -fV=-0.01 -> localization:動的局在化(expの場合、1次元の拘束条件で特異点を生成) -fV=0.01,V0=0:同上のdouble-check ・Gross-Pitaevskii:Ver.2.801.128以降、1次元のGross-Pitaevskii方程式(理想Boson多体系の基底状態を記述) ⇒Bose-Einstein凝縮:非線形なSchrödinger方程式でplot毎にt=0から時間発展のため、非常に重い(未最適化) -Gauss-abs:Ver.2.804.130以降、Gauss波束の確率分布|ψ(x)|^2(大域的な確率保存則を確認) -V=0:V(x)=0の波動関数ψ0(x)∝x**2の分散と干渉過程を明示 ・(φ,A):Ver.2.803.128以降、電磁場中の荷電粒子の1次元Schrödinger方程式(実数の4元potentialで記述) 非相対論の仮定:Lorentz因子=1(相対論の場合、Hamiltonian内の根号を消去する工夫が必要) 空間Δ||∇演算子の離散化:後述のadvection-diffusion方程式に同様 -Gauss-abs:Ver.2.804.130以降、Gauss波束の確率分布|ψ(x)|^2(大域的な確率保存則を確認) -fA=1~0:φ(t)=0, A(t)∝sin(2pi*fA*t) ⇒位相変化の周波数応答fA=1→0.01→0:対称性 ⇒ 非対称性 ⇒ 対称性 -A(x,t)-fA=1~0:A(x,t)の空間依存性を仮定(周期境界条件) ⇒位相変化の周波数応答fA→0:対称性の乱れ ⇒ 動的局在化(初期状態ψ0に依存しない) ・Dirac:Ver.2.799.127以降、1次元Dirac方程式のadaptive-stepの時間発展(波動関数ψ1~4の時間と空間を強連成) 空間∇演算子の離散化:中心差分法(境界条件を含むarea参照と拡張行列演算で記述) ⇒後述の数値粘性のschemeなし:Ver.2.799.128以降、非物理的な数値振動を解消(reshaper ⇒ reshapec) ⇒行列積の演算順序の交換関係:L*R=(R.*L.). 境界条件の仮定:ψ"(x)=0相当の線形外挿(部分空間の確率として、成行きflux∝ψ'(x)≠0を許容) -Gauss-abs -> fluctuation:Ver.2.804.130以降、Gauss波束の確率分布|ψ(x)|^2(大域的な確率保存則を確認) ⇒V(x)=0:相対論のFermionが従う時空の量子ゆらぎを明示(差分刻みdxに依存しない) ⇒real||imag(ψ(x)):対称性||非対称性(ψ1~4の初期値に依存) -flux=0||-mirror||-periodic:境界条件をextrapolationから変更(ψ'(x)=0相当||鏡映||周期境界条件) ⇒対称性の破れの遷移状態:大差なし(以降、周期境界条件を適用) -ψ1~4-abs:Dirac表現の波動関数ψ1~4の確率分布|ψ(x)|^2 ⇒一致のpair:なし -Weyl-ψ1~4-abs:Weyl表現の波動関数ψ1~4の確率分布|ψ(x)|^2 ⇒一致のpair:|ψ2|=|ψ3|, |ψ4|=|ψ1| -Majorana-ψ1~4-abs:Majorana表現の波動関数ψ1~4の確率分布|ψ(x)|^2 ⇒一致のpair:|ψ1|=|ψ3|, |ψ2|=|ψ4| ⇒表現の任意性(4成分の上下半分でspin状態を区別):|ψ1|=Weyl表現の|ψ2|, |ψ2|=Weyl表現の|ψ1| -V(x,t)-exp||cos(fV=0):動的局在化(expの場合、1次元の拘束条件で特異点を生成) ⇒相対論のFermion:非相対論のBoson同様の解釈(Schrödinger1d参照) -V=0:V(x)=0の波動関数の振動過程を明示 ⇒Fermion:分散を伴うBosonと異なる挙動 ・wave-equation:1次元の波動方程式(上記のSchrödinger方程式に同様の記述) ⇒波面:初期状態の回帰過程を明示 -Gauss:Ver.2.804.129以降、Gauss波束の場合、分散なしを確認 ・Klein-Gordon:1次元のKlein-Gordon方程式(上記の波動方程式にspring項を導入の電信方程式) +damper:damper項を導入 ・diffusion:1次元の拡散方程式 ・advection:1次元の移流方程式(上記の波動方程式の一方向の移流を記述) ⇒中心差分法:非物理的な数値振動を明示 -scheme=o1~o3:1~3次精度の上流差分 ⇒数値粘性:非物理的な数値振動を抑制(分子粘性に同様の効果) advection-diffusion:1次元の移流拡散方程式(上記の移流方程式に分子粘性の拡散項を導入) ・Bateman-Burgers:1次元のBateman-Burgers方程式(上記の移流拡散方程式の移流速度が場に依存) ・Langevin:Ver.2.794.126以降、1次元のLangevin方程式(確率微分方程式) ⇒cの仮定:粒子sizeの影響(m相当)を含むdamper係数 ・Brown:Ver.2.794.126以降、2次元Brown運動の軌跡(上記のLangevin方程式を複素数演算で記述) ⇒確率項の仮定:各軸独立の力∝標準正規分布に従うN(0,1)の乱数 ⇒試行回数→∞:環境不変のwhite-noiseの場合、平均2乗変位∝step(等方性の等速運動に相当) +spring:spring項を導入 ⇒spring||damper項:係数大で拡散距離が減衰 ・random-walk:2次元random-walkの軌跡(3次元の投影でない最も単純な記述) ⇒自己相似性:1stepの拡散距離∝1/分子粘性係数(粒子sizeの影響を未考慮) ・DLA:2次元の拡散律速凝集の上面図(原点の核成長を複素数演算で記述) -side:側面図をy=0と上半平面にplot(y=0の3点の核成長を記述) ・Penrose:Penroseの非周期tilingの1種(菱形のpairを作る再帰的な複素数演算で記述) Ver.2.840.145以降、高速化(1setの入力v0を複製 ⇒ 1setの出力arr_z0をpushでmakeして複製) -mirror:Ver.2.845.153以降、大域的な鏡映対称性(黄金triangle起源) ⇒菱形のtriangle-pair:◇ -rotation:大域的な5回の回転対称性(黄金triangle起源) +mirror:Ver.2.840.145以降、鏡映対称性を追加(hasMirror) ⇒原点の頂点を変更:jv=1⇒2⇒0(全3点の列挙順序) -sun:sunのdeflation||decomposition(36°頂点) -star:starのdeflation||decomposition(非可換の72°頂点) -gnomon-rotation:Ver.2.845.153以降、大域的な5回の回転対称性(黄金gnomon起源) -mirror:大域的な鏡映対称性(黄金gnomon起源) ⇒菱形のgnomon-pair:◆ +rotation:Ver.2.840.145以降、5回の回転対称性を追加(Nrotation) Ver.2.845.153以降、修正 ⇒原点の頂点を変更:jv=2⇒0⇒1(全3点の列挙順序) -star:Ver.2.845.153以降、starのdeflation||decomposition(可換の36°頂点) ⇒sunとstarの相互変換:◇=kite-dart ⇔ ◆=kite+dart ⇒星型多面体の準結晶の投影図(白枠のsun部分):☆+(◇+kite)*5(Ver.2.851.157以降、compositesを適用) -star:同上のひずみ分布と奥行きの表現(Ver.2.846.153~2.848.155以降、mrcolorsとcompositesを適用) -complement:Ver.2.840.145以降、平面充填の相補的な対称性(黄金triangle+gnomon起源) ⇒相補的な対称性:sunのtriangle☆⇒gnomon★に反転表示で★の欠損なし(境界を含む) +mirror -> sun-filling:同上のdouble-check(matching規則を満たす三角形の全対称性) ⇒☆+★のsun部分:平面充填を明示(Ver.2.846.153~2.851.157以降、mrcolorsとcompositesを適用) -variant:同上の変種tiling(triangleの36°頂点近傍で規則性なし) -pattern~:同上の規則的なpattern(Ver.2.851.157以降、mrcolorsとcompositesを適用) -galaxy:渦巻銀河の腕を含む差動回転と螺旋構造の表現(5bodyの密度波の重複許容tiling) ⇒matching規則を満たさない重複部分:観測困難で不確定な領域 ・pinwheel~-Z:回転対称性の平面充填曲線||fractal(再帰的な複素行列演算で記述) ・Pythagoras:Pythagoras tree(再帰的な複素行列演算で記述) ・Lévy-l1:回転対称性のfractal曲線(Iterated Function Systemで記述) ・rule90:Sierpinski gasket(Cellular Automatonで記述) ・gradation:gradation特定項目仕様の実施例 |
| 項目 | 内容 |
|---|---|
|
参考Docs
(解釈) |
参考Docs(解釈)について記述する
各domain||linkの項目を以下に列挙する fnorio.com ・36. 虹の理論 ・40. 温室効果と地球温暖化 ・85. 惑星探査機のスイングバイ航法 ・125. プランクの熱輻射法則(1900年) ・128. 電磁場中の荷電粒子の運動(Lagrangian、Hamiltonian) slpr.sakura.ne.jp/qp/ ・弾道計算(BB弾)の理論 ・電磁場中の荷電粒子に対する非相対論的シュレーディンガー方程式から双極子近似まで ・最速・高精度の数値積分 ・二重指数関数型数値積分 mathematica.site ・5-3.ピラミッドの『黄金比の謎』を解明する hypertree.blog.ss-blog.jp ・No.315 - 高校数学で理解する楕円曲線暗号の数理(1) num-kt.com ・Processing ペンローズ・タイルの実装 storytellphys.wordpress.com ・Gauss波束 ・Dirac方程式 ・Diracのガンマ行列 eng.niigata-u.ac.jp/~nomoto/ ・複素数の指数関数・対数関数・べき関数 ・ディラック方程式 physics.okayama-u.ac.jp/~otsuki/lecture/CompPhys2/ ・8.2. 【例題】ボーズ・アインシュタイン凝縮の比熱 home.hirosaki-u.ac.jp/relativity/ ・複素フーリエ級数 butsuri.it-chiba.ac.jp/~yasutake/matter/onodera_abc-conjecture.pdf ・abc予想入門 avi-loeb.medium.com ・ʻOumuamua Was Not a Hydrogen-Water Iceberg ・Is the 0.2% Outlier-Fraction of Meteorites from an Interstellar Origin? ・Is the Interstellar Object 3I/ATLAS Alien Technology? ・Was the "Wow! Signal" Emitted from 3I/ATLAS? ・New Questions and Answers About 3I/ATLAS ・An Extraordinary New Anomaly of 3I/ATLAS ・Images of 3I/ATLAS on November 22–24, 2025 ・Updates on the Non-gravitational Acceleration of 3I/ATLAS ・First X-Ray Detection of 3I/ATLAS ・3I/ATLAS is Green After Perihelion ・The Anti-Tail of 3I/ATLAS is Larger Than the Distance to the Moon ・The Anti-Tail of 3I/ATLAS Wobbled Before Perihelion ・A 14th Anomaly of 3I/ATLAS Alignment of Its Rotation Axis with the Sunward Direction at Large Distances ・Europa Clipper Observed 3I/ATLAS Near Perihelion ・Will Material from 3I/ATLAS Arrive on Earth? ・New Radio Data and Diameter Estimate for 3I/ATLAS ・The Dust Mass Shed by 3I/ATLAS ・If 3I/ATLAS is a Comet, then Its Anti-Tail Jet Should Not Include Streaming Gas Beyond ~5,000 kilometers ・The Symmetric Jet Structure in Hubble Images of 3I/ATLAS |
|
参考Docs
(仕様) |
参考Docs(仕様)について記述する
各domain||linkの項目を以下に列挙する developer.mozilla.org/ja/docs/ ・浮動小数点数 ・Number ・Element: wheel イベント ・SVG要素リファレンス keisan.casio.jp ・ベッセル関数 ・双曲線正弦積分 ・双曲線余弦積分 ・楕円積分 ・二重指数関数型数値積分 ・積分で求めるガンマ関数 science.nasa.gov/solar-system/comets ・3i-atlas ssd.jpl.nasa.gov/tools ・sbdb_lookup.html swpc.noaa.gov/products ・real-time-solar-wind sos70.ru ・Space Observing System 70 |
| 参考Wikipedia |
参考Wikipediaについて記述する
en.m.wikipedia.org/wiki/項目を列挙する ・Gaussian_elimination ・Tridiagonal_matrix_algorithm ・Standard_normal_table ・Pareto_distribution ・Logistic_distribution ・Weibull_distribution ・Fréchet_distribution ・Laplace distribution ・Lambert_W_function ・Bessel_function ・Airy_function ・Gegenbauer_polynomials ・Laguerre_polynomials ・Butterfly_curve_(transcendental) ・List_of_fractals_by_Hausdorff_dimension ・Moore_curve ・Sierpiński_curve ・Minkowski_sausage ・Pythagoras_tree_(fractal) ・Penrose_tiling ・Golden_ratio ・Metallic_mean ・Simple_continued_fraction ・Compton_scattering ・Linear_congruential_generator ・Lehmer_random_number_generator ・List_of_Runge-Kutta_methods ・Bogacki-Shampine_method ・Dormand-Prince_method ・Magnus_effect ・Kepler's_equation ・Kepler's_laws_of_planetary_motion ・Lunar_precession ・Pythagorean_theorem ・Fermat's_Last_Theorem ・Frey_curve ・Elliptic_curve ・Birch_and_Swinnerton-Dyer_conjecture ・Hasse-Weil_zeta_function ・Prime_zeta_function ・Riemann_hypothesis ・Riemann_zeta_function ・Euler-Maclaurin_formula ・Möbius_function ・Argument_principle ・Riemann_xi_function ・Functional_equation ・Gamma_function ・Reflection_formula ・Stirling_numbers_of_the_first_kind ・Abc_conjecture ・Collatz_conjecture ・Goldbach's_conjecture ・Mertens_conjecture ・Bisection_method ・Synchronicity ・Nikola_Tesla ・Magic_square ・Great_Pyramid_of_Giza ・Maxwell's_equations ・Burgers'_equation ・Langevin_equation ・Langevin_dynamics ・Bose-Einstein statistics ・Maxwell-Boltzmann_statistics ・Fermi-Dirac_statistics ・Dirac_equation ・Gamma_matrices ・Piezoelectricity ・Coriolis_force ・Deep_learning ・Lidar ・Paris_Agreement ・Lorenz_system ・Logistic_differential_equation ・Stefan-Boltzmann_law ・Murphy's_law ・Von_Neumann_stability_analysis ・Monte_Carlo_method ・Fisher-Yates_shuffle ・Enigma_machine ・Rotation_formalisms_in_three_dimensions ・CIE_1931_color_space ・HSL_and_HSV ・Aurora ・Rainbow ・Hopi ・3I/ATLAS ・GRB_250702BDE ・Wow!_signal ・Voyager_1 ・Voyager_2 ・Voyager_Golden_Record ・1977 ・1977_in_film ・C/2025_F2_(SWAN) ・C/2025_R2_(SWAN) ・C/2025_A6_(Lemmon) ・Comet_ATLAS ・Comet_Encke ・Pan-STARRS ・Comet ・Extinct_comet ・Lists_of_comets ・Lists_of_telescopes ・DarkSky_International ja.m.wikipedia.org/wiki/項目を列挙する ・JavaScriptエンジン ・MATLAB ・先読み ・遅延評価 ・カリー化 ・無名再帰 ・相互再帰 ・演算子の優先順位 ・三項演算子 ・条件演算子 ・結合法則 ・剰余演算 ・IEEE_754 ・誤差 ・精度保証付き数値計算 ・二重指数関数型数値積分公式 ・線形合同法 ・複素数の偏角 ・三角積分 ・指数積分 ・対数積分 ・対数微分 ・複素対数函数 ・対数 ・四元数 ・行列 ・疎行列 ・行列の乗法 ・内積 ・直積_(ベクトル) ・クロス積 ・アダマール積 ・ヤコビ行列 ・ニュートン法 ・割線法 ・二分法 ・解析接続 ・零点 ・極値 ・変曲点 ・留数 ・極_(複素解析) ・偏角の原理 ・有理型関数 ・調和級数 ・メルカトル級数 ・オイラーの式 ・オイラーの和公式 ・オイラー積 ・オイラーの定数 ・約数関数 ・オイラーのφ関数 ・オイラーの五角数定理 ・オイラー数 ・ネイピア数 ・フィボナッチ数 ・スターリング数 ・アペリーの定数 ・アペリーの定理 ・双子素数 ・素数定理 ・素数計数関数 ・確率の公理 ・ゲーデルの不完全性定理 ・数学上の未解決問題 ・ポアンカレ予想 ・リーマン予想 ・バーチ・スウィンナートン=ダイアー予想 ・ABC予想 ・コラッツの問題 ・ゴールドバッハの予想 ・谷山-志村予想 ・フェルマーの最終定理 ・フェルマーの小定理 ・特殊関数 ・L-函数 ・ベータ関数 ・ベータ分布 ・カイ二乗分布 ・不完全ガンマ関数 ・ガンマ関数 ・ディガンマ関数 ・ポリガンマ関数 ・ガンマ分布 ・ポアソン分布 ・コーシー分布 ・ボース分布関数 ・マクスウェル分布 ・フェルミ分布関数 ・ベッセル関数 ・エアリー関数 ・バーガース方程式 ・移流拡散方程式 ・ランジュバン方程式 ・確率微分方程式 ・硬い方程式 ・累積分布関数 ・誤差関数 ・正規分布 ・対数正規分布 ・ジップの法則 ・二項分布 ・パスカルの三角形 ・二項係数 ・ライプニッツの公式 ・ガウス積分 ・オイラー積分 ・ハッセ・ヴェイユのゼータ函数 ・リーマンゼータ関数 ・ベルヌーイ数 ・ベルヌーイ多項式 ・ファウルハーバーの公式 ・ロドリゲスの公式 ・ルジャンドル多項式 ・エルミート多項式 ・チェビシェフ多項式 ・ガウスの消去法 ・関孝和 ・エイトケンのΔ2乗加速法 ・総和 ・有限差分 ・微分の記法 ・線形システム論 ・放物型偏微分方程式 ・斜方投射 ・ルンゲ=クッタ法 ・ルンゲ=クッタ法のリスト ・ルンゲ=クッタ=フェールベルグ法 ・ルンゲ現象 ・ユークリッドの互除法 ・クロネッカーのデルタ ・最小二乗法 ・ラグランジュ補間 ・スプライン曲線 ・B-スプライン曲線 ・シグモイド ・シグモイド関数 ・サイクロイド ・クロソイド曲線 ・カテナリー曲線 ・楕円曲線 ・J-不変量 ・楕円曲線暗号 ・楕円 ・アレニウスの式 ・デデキントのイータ関数 ・ラマヌジャンのタウ函数 ・モジュラー形式 ・双曲線関数 ・逆双曲線関数 ・三角関数 ・逆三角関数 ・宇宙_(数学) ・濃度_(数学) ・マンデルブロ集合 ・充填ジュリア集合 ・バーニングシップ・フラクタル ・ディラックのデルタ関数 ・ヘヴィサイドの階段関数 ・カントール関数 ・高木曲線 ・ワイエルシュトラス関数 ・ディリクレの関数 ・ブラウン運動 ・拡散律速凝集 ・エノン写像 ・バーンズリーのシダ ・コッホ曲線 ・ペンローズ・タイル ・準結晶 ・星型多面体 ・黄金三角形 ・黄金長方形 ・空間充填曲線 ・超球面 ・L-system ・ヒルベルト曲線 ・Z階数曲線 ・ペアノ曲線 ・ドラゴン曲線 ・レヴィC曲線 ・シェルピンスキーのギャスケット ・シンプソンの公式 ・ラプラス変換 ・フーリエ変換 ・フーリエ級数 ・アイゼンシュタイン級数 ・実解析的アイゼンシュタイン級数 ・三角波_(波形) ・高速フーリエ変換 ・ハールウェーブレット ・多重解像度解析 ・重ね合わせの原理 ・暗号 ・コード_(暗号) ・ガンマ補正 ・グレースケール ・ジュール熱 ・情報量 ・エントロピー ・熱力学第二法則 ・断熱過程 ・ロビン境界条件 ・カルノーサイクル ・オットーサイクル ・ディーゼルサイクル ・スターリングエンジン ・太陽活動周期 ・太陽フレア ・太陽風 ・コロナ質量放出 ・コロナグラフ ・磁気嵐 ・磁気リコネクション ・ローレンツ力 ・オーロラ ・太陽定数 ・太陽放射 ・放射輝度 ・ウィーンの変位則 ・プランクの法則 ・レイリー・ジーンズの法則 ・ミランコビッチ・サイクル ・太陽エネルギー ・プリズム ・地球 ・北半球 ・熱赤道 ・地球のエネルギー収支 ・パリ協定_(気候変動) ・温室効果 ・熱放射 ・放射強制力 ・全球気候モデル ・地球の大気 ・空気力学 ・空力弾性 ・ローリング ・衝撃波 ・ソニックブーム ・極渦 ・ジェット気流 ・飛行機雲 ・翼型 ・仰俯角 ・よどみ点 ・PID制御 ・ストークスの定理 ・循環_(流体力学) ・大気循環 ・国際標準大気 ・窒素 ・酸素 ・アルゴン ・二酸化炭素 ・暴走温室効果 ・気候感度 ・エアロゾル ・火山 ・災害 ・大量絶滅 ・年代測定 ・氷期 ・最終氷期 ・氷床 ・氷河時代の年表 ・ヤンガードリアス ・マウンダー極小期 ・ジャイアント・インパクト仮説 ・トバ・カタストロフ理論 ・ホモ・サピエンス ・人類の進化 ・更新世 ・完新世 ・海面上昇 ・海水準変動 ・熱膨張率 ・縄文時代 ・縄文海進 ・時定数 ・マグニチュード ・プレート ・電力系統 ・ヴァンデグラフ起電機 ・レッドスプライト ・カーマン・ライン ・大気圏 ・対流圏 ・成層圏 ・電離層 ・熱圏 ・磁気圏 ・ヴァン・アレン帯 ・エッジワース・カイパーベルト ・バミューダトライアングル ・ビミニ・ロード ・富士山 ・安息角 ・星空保護区 ・太陽系 ・水星 ・金星 ・火星 ・木星 ・土星 ・天王星 ・海王星 ・冥王星 ・銀河系 ・銀河群 ・銀河団 ・超銀河団 ・銀河フィラメント ・渦巻銀河 ・銀河の回転曲線問題 ・宇宙の大規模構造 ・宇宙ジェット ・ハビタブルゾーン ・スケーラビリティ ・カルダシェフ・スケール ・ダイソン球 ・フェルミのパラドックス ・パンスペルミア説 ・宇宙文明 ・プラズマ宇宙論 ・電磁流体力学 ・デリンジャー現象 ・宇宙天気予報 ・ポールシフト ・地磁気逆転 ・仮説上の天体 ・オールトの雲 ・太陽系外縁天体 ・準惑星 ・惑星質量天体 ・惑星X ・ニビル_(仮説上の惑星) ・プルーネット ・スイングバイ ・脱出速度 ・原始惑星系円盤 ・超新星 ・金属カルボニル ・硫化カルボニル ・カルボニル基 ・彗星 ・大彗星 ・マンクス ・サングレーザー ・クロイツ群 ・ディディモス_(小惑星) ・Hera_(探査機) ・エンケ彗星 ・紫金山・アトラス彗星 ・周期彗星 ・非周期彗星 ・ヘール・ボップ彗星 ・ハレー彗星 ・ハレー型彗星 ・核_(彗星) ・尾_(彗星) ・オウムアムア ・ボリソフ彗星_(2I/Borisov) ・3I/ATLAS ・小惑星地球衝突最終警報システム ・ファルネーゼのアトラス ・ガンマ線バースト ・Wow!_シグナル ・三十六進法 ・21cm線 ・空中線電力 ・地球外知的生命体探査 ・ボイジャー計画 ・ボイジャーのゴールデンレコード ・1977年 ・1977年の映画 ・長楕円軌道 ・反地球 ・超流動 ・超伝導 ・室温超伝導 ・経験則 ・ボディマス指数 ・ハインリッヒの法則 ・ムーアの法則 ・観天望気 ・ケプラーの法則 ・ケプラー方程式 ・三体問題 ・N体シミュレーション ・二重振り子 ・直交座標系 ・球面座標系 ・円錐曲線 ・立体角 ・真近点角 ・平均近点角 ・離心近点角 ・赤道傾斜角 ・黄道傾斜角 ・軌道傾斜角 ・軌道離心率 ・太陽質量 ・地球質量 ・公転 ・1_E11_m ・点対称 ・線対称 ・月 ・月の軌道 ・軌道力学 ・抗力 ・慣性モーメント ・多体問題 ・重力圏 ・ヒル球 ・ロッシュ限界 ・潮汐 ・潮汐力 ・自転と公転の同期 ・ヤルコフスキー・オキーフ・ラジエフスキー・パダック効果 ・ヤルコフスキー効果 ・ポインティング・ロバートソン効果 ・摂動_(天文学) ・章動 ・地震学における脈動 ・地磁気 ・歳差運動 ・近点移動 ・近点月 ・天の川 ・黄道十二星座 ・黄道帯 ・天文単位 ・公転周期 ・惑星直列 ・位相角_(天文学) ・合_(天文) ・衝 ・雪線_(天文学) ・年 ・地球史年表 ・スノーボールアース ・屈折ピラミッド ・三大ピラミッド ・カフラー王のピラミッド ・メンカウラー王のピラミッド ・ギザの大スフィンクス ・クフ ・カフラー ・メンカウラー ・ビッグバン ・宇宙の終焉 ・宇宙の年齢 ・地球の年齢 ・銀河年 ・ユリウス年 ・干支 ・辛酉 ・グレゴリオ暦 ・プラズマ ・エネルギー準位 ・フォノン ・コンクリート ・時空 ・シミュレーション仮説 ・量子コンピュータ ・反物質 ・共振 ・シューマン共振 ・脳波 ・シナプス ・自励振動 ・赤方偏移 ・青方偏移 ・ドップラー効果 ・相対性原理 ・特殊相対性理論 ・一般相対性理論 ・相対性理論 ・ローレンツ変換 ・ミンコフスキー空間 ・時間の遅れ ・タキオン ・不確定性原理 ・波長 ・光子 ・偏光 ・散乱 ・レイリー散乱 ・チンダル現象 ・レンズフレア ・格子振動 ・ホログラフィー ・コヒーレント状態 ・ボース=アインシュタイン凝縮 ・BCS理論 ・超伝導 ・高温超伝導 ・室温超伝導 ・因果集合 ・因果性 ・弁証法 ・二元論 ・陰陽 ・インフレーション理論 ・宇宙のインフレーション ・アインシュタイン方程式 ・フリードマン・ルメートル・ロバートソン・ウォーカー計量 ・フリードマン方程式 ・宇宙論パラメータ ・宇宙定数 ・ハッブル-ルメートルの法則 ・宇宙背景放射 ・観測可能な宇宙 ・事象の地平面 ・光年 ・Weakly_interacting_massive_particles ・暗黒物質 ・ダークエネルギー ・基本相互作用 ・強い相互作用 ・弱い相互作用 ・ワインバーグ=サラム理論 ・大統一理論 ・統一場理論 ・超弦理論 ・量子重力理論 ・隠れた変数理論 ・多元宇宙論 ・多世界解釈 ・コペンハーゲン解釈 ・フォン・ノイマン=ウィグナー解釈 ・ボーム解釈 ・トンネル効果 ・波動方程式 ・電信方程式 ・クライン-ゴルドン方程式 ・ディラック方程式 ・ガンマ行列 ・パウリ行列 ・グロス=ピタエフスキー方程式 ・シュレーディンガー方程式 ・波束 ・波動関数 ・波動関数の収縮 ・対称性の破れ ・対称性 ・ベルの不等式 ・観測問題 ・量子力学 ・量子ゆらぎ ・量子もつれ ・量子ゼノン効果 ・量子デコヒーレンス ・ホログラフィック原理 ・自己相似 ・般若心経 ・六道 ・天_(仏教) ・涅槃 ・神道 ・陰陽道 ・天文道 ・占星術 ・瞑想 ・虚空 ・意識 ・無意識 ・悟り ・他力本願 ・自我 ・業 ・輪廻 ・老子 ・釈迦如来 ・弥勒菩薩 ・観音菩薩 ・十一面観音 ・勢至菩薩 ・阿弥陀如来 ・地蔵菩薩 ・地涌の菩薩 ・ホピ族 ・シリウス ・オリオン座 ・プレアデス星団 ・北斗七星 ・柄杓 ・カタカムナ文献 ・三相交流 ・三位一体 ・最後の審判 ・ガイア理論 ・地球の構造 ・感覚器 ・脳 ・神経 ・デオキシリボ核酸 ・塩基対 ・細胞周期 ・DNA修復 ・細胞分裂 ・テロメア ・ヘイフリック限界 ・細胞 ・植物細胞 ・セル・オートマトン ・フラクタル |
| 参考天文学辞典 |
参考天文学辞典について記述する
astro-dic.jp/項目を列挙する ・neutral-atomic-hydrogen ・charge-exchange-reaction ・outburst ・multiple-coulomb-scattering ・segmented-mirror ・segmented-mirror-telescope ・spatial-resolution ・diffraction-spike ・expression-of-angle ・ecliptic ・ecliptic-coordinate-system ・galactic-plane ・galactic-halo ・hill-radius ・roche-limit |
| 参考JSME-MED |
参考JSME-MEDについて記述する
jsme.or.jp/jsme-medwiki/検索項目を列挙する ・ニュートン・ラプソン法 ・エントロピー条件 ・ボーズ・アインシュタイン統計 ・フェルミ・ディラック統計 ・圧縮性流れ ・混合距離 ・散逸 ・自励振動 |
| 参考GitHub |
参考GitHubについて記述する
domainを列挙する ・github.com/numpy ・utokyo-ipp.github.io |
| 参考URL |
参考URLについて記述する
domainを列挙する ・wikipedia.org ・astro-dic.jp ・jsme.or.jp ・developer.mozilla.org ・gemini.google.com ・support.microsoft.com ・mathworks.com ・wolframalpha.com ・keisan.casio.jp ・oeis.org ・lmfdb.org ・sagecell.sagemath.org ・numpy.org |
| 参考映像 |
参考映像について記述する
viewer ・theskylive.com 天体写真 ・app.astrobin.com ・astroarts.co.jp YouTube ・【公式】名古屋市科学館:2025年11月25日 オンライン市民観望会「土星」 ・国立天文台 (NAOJ):土星の環が消える!? 天文学者と楽しむ『土星の環の消失』 ・ごーしん真理ラボ:ガンマ線バースト検出 3I/ATLASとの奇妙な関連 ・ごーしん真理ラボ:25Hz信号3I/ATLAS接近と同時に受信 シューマン共振データに何が? ・哲理学作家さとうみつろう:純正律カノン瞑想 "2026冬至点" Mi To ki |
| 参考論文 |
参考論文について記述する
title/発行元(発行年)を列挙する 1. THERMAL-ELECTROCHEMICAL COUPLED MODELING OF A LITHIUM-ION CELL Proceedings of the ECS(2000) 2. 宇宙膨張と宇宙論パラメータ 2009_Bthesis_kuroda.pdf(2009年度 卒業論文) 3. A formula for Ramanujan's τ-function Illinois J. Math. 19(3) 448-449 (1975) 4. 噴霧流動場に形成される渦構造の可視化と噴霧の先端到達距離に関する研究 第13章 噴霧の先端到達距離に関する理論の体系化(2008年度 博士論文) 第7章 噴霧のサブモデル(校正の指摘) ・Equation (7.3.2):d32のmoment次数の定義 ・Equation (7.3.7):exp(-β ⇒ exp(-B ・Figure 7.3.3:Nukiyama-Tanasawa分布(2)の再現性 |
| 項目 | 内容 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
目次
4次元時空 の解釈 |
4次元時空の解釈について記述する
keyword ・時空・時間・空間 ・統一場理論・超弦理論・量子重力理論 ・多元宇宙論・(相互干渉)多世界解釈・Copenhagen解釈 ・simulation仮説・量子computer・energy ・生命・意識・物質・反物質・非物質 ・振動数・共振・周期・周波数・vibration ・相対性原理・光速度不変の原理 ・相対性理論・Minkowski空間・時間ゆがみ・tachyon ・不確定性原理・光子・波動関数・tunnel効果・量子ゆらぎ・量子Zeno効果・量子decoherence ・因果集合理論・因果性・二極化・二元論・陰陽・量子もつれ・synchronicity ・inflation理論・宇宙背景放射・暗黒物質・暗黒energy ・black hole・holographic原理・entropy・singularity・特異点 ・自己相似・色即是空・空即是色・原点回帰 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
空間次元 の解釈 |
空間次元の解釈について記述する
数学 ・次元:D ・Pascalの三角形:二項係数の総和=2**(D+1) D=1; _s((k)=<combin(n,k),n=D+1,n) -> 4 D=3; _s((k)=<combin(n,k),n=D+1,n) -> 16 D=5; _s((k)=<combin(n,k),n=D+1,n) -> 64 超四面体 ・頂点:上+1 ⇔ 辺以降:左上+上×1 ⇔ 総和=2**(D+1)-1 頂点 辺 面 胞 ・・・ D=0 1 D=1 2 1 D=2 3 3 1 D=3 4 6 4 1 D=4 5 10 10 5 1 D=5 6 15 20 15 6 1 超立方体 ・頂点:上×2 ⇔ 辺以降:左上+上×2 ⇔ 総和=3**D 頂点 辺 面 胞 ・・・ D=0 1 D=1 2 1 D=2 4 4 1 D=3 8 12 6 1 D=4 16 32 24 8 1 D=5 32 80 80 40 10 1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
現宇宙 の解釈 |
現宇宙の解釈について記述する
前提 ・赤方偏移:膨張由来(光の減衰なし) 定義 ・時間:t 創成:t=0 現在:t=t0 ・scale因子:a(t) 創成:a(0)=0 現在:a(t0)=1 ・温度:T(t) 密度 ・放射:energy密度∝1/a**4 ・物質:密度∝1/a**3 ・等密度:放射と物質のenergy密度が一致 質量とenergyの等価性:energy=質量m*光速c**2 温度 ・放射優勢期:放射と物質が熱平衡(Tr=Tm=T) 放射と物質:T∝t**(-1/2) ・物質優勢期:放射と物質の温度が非平衡(Tr>Tm) 放射:Tr∝t**(-2/3) 物質:Tm∝t**(-4/3) 時空の運動方程式 ・観測結果と整合の仮定:「平坦で一様等方性」 ・Friedmann方程式:次のFLRW計量の物質分布を完全流体近似 Friedmann-Lemaître-Robertson-Walker計量:一般相対性理論のEinstein方程式の1厳密解 描像 ・inflation:a∝exp(係数*t) 一連の仮説:無⇒量子ゆらぎ⇒負の圧力⇒真空の膨張⇒過冷却⇒真空の相転移⇒熱変換⇒big-bang ・放射優勢期:a∝t**(1/2) 約5万年後:等密度@T=1e4[K] 約38万年後:宇宙の晴れ上がり@Tr=3000[K] ・物質優勢期:a∝t**(2/3) 約2億年後:初代天体の形成@Tr=30[K] 約69億年後:減速⇒加速の変曲点@Tr=5[K] ・後期加速膨張:a∝exp(係数*t)**(2/3) 約138億年後:現在@Tr=3[K] ・発散期:未知数 減衰あり:均一な熱平衡状態に到達||収縮に反転 減衰なし:全物質が素粒子まで分解(基本相互作用の媒介不能) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
赤方偏移 の解釈 |
赤方偏移の解釈について記述する
分類 ・宇宙論的赤方偏移:Hubble膨張に由来 波長:λ scale比:r=観測λ/元λ=a(現在)/a(過去) 無次元偏移:z=r-1 ・運動学的赤方||青方偏移:光源と観測者の相対速度(離脱||接近)のDoppler効果に由来 ・重力赤方||青方偏移:重力potentialの一般相対性理論に由来 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
「平坦で 一様等方性」 の解釈 |
「平坦で一様等方性」の解釈について記述する
Poincaré予想のPerelman証明(西暦2002~2006年) ・W汎関数増大の単調性 Gemini 2.5 Flash「W汎関数の増大は、 リッチフローが多様体の幾何学的情報をある種の「標準形」へと収束させていく過程であり、 その過程で、元の多様体が持っていた詳細で複雑な情報の一部が「失われていく」と解釈できるということです。」 ⇒Ver.2.871.163以降、entropyと混同不可 時空の定義 ・時間:t ・空間 次元:D 形状因子:b 曲率:k(t) 曲率半径:r(t):=1/k 体積:V(t):=b*r**D 非厳密な仮定 Ver.2.871.163以降、追記して修正 ・初期値が正:V(0)>0 ⇔ k(0)>0 ・孤立系:等温過程の不可逆な断熱自由膨張(圧力の仕事を未考慮) ・時空のみを考慮(重力を未考慮) 関係式 r=1/k r**D=(1/k)**D V=b*(1/k)**D ln(V)=ln(b)+D*ln(1/k) ln(V)∝ln(1/k) entropy定義の任意性 entropy∝ln(V) 情報量∝log2(1/k) ・black hole:事象の地平面の表面積 entropy増大則 V(+∞)=+∞ k(+∞)=0 「平坦で一様等方性」 ・時空の制約条件:entropy∝ln(体積)∝log2(1/|曲率|) ・entropy増大則:無限小の空間から膨張で曲率は平坦化に向かう |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
発散系 の解釈 |
発散系の解釈について記述する
仮定 ・「平坦で一様等方性」 定義 ・半径[m] 現在:rnow ・球の体積[m^3] 現在:Vnow 過去:Vpast ・系のquality:quality:=ln(Vnow)/ln(Vpast) 現宇宙は発散系(平衡点の系のquality≥2) ・現在(観測可能範囲) V(r)=<(4pi/3)*r**3; Vpast(quality)=<e**(ln(Vnow)/quality); rnow=465e8*9460730472580800; Vnow=V(rnow); Vnow -> 3.5663295987161737e+80 Vpast(1) -> 3.566329598716132e+80 ・宇宙の晴れ上がり(最終散乱面) Vre=V(rnow/1e3); Vre -> 3.566329598716174e+71 qualityre=ln(Vnow)/ln(Vre); qualityre -> 1.125782258245689 ・初期宇宙 Vpast(2) -> 1.8884728218102934e+40 Vpast(2**8) -> 2.063750137225363 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
統一場理論 の解釈 |
統一場理論の解釈について記述する
統一理論の定義 ・超大統一理論(統一場理論):大統一理論に重力を統一(万物の理論) ・大統一理論:電弱統一理論に強い力を統一(未完成) ・電弱統一理論:弱い力と電磁力を統一(西暦1967年に完成) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
相互作用 の解釈 |
相互作用の解釈について記述する
基本相互作用の相対的な強さ(重力基準) ・強い力:10**40 ・電磁力:10**38 ・弱い力:10**15 ・重力:10**0=1 基本相互作用の影響範囲[m] ・強い力:10**(-15) ・電磁力:無限大(力∝1/距離**2) ・弱い力:10**(-18) ・重力:無限大(力∝1/距離**2) 基本相互作用の補足 ・強い力:原子核とその核子(陽子||中性子)が崩壊しないように束縛する核力 ・弱い力:ある粒子を別の粒子に変える力(主にβ崩壊の原因となる力) β崩壊:原子核内の中性子を陽子に変換して電子を放出する現象 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
gravity の解釈 |
gravityの解釈について記述する
重力 ・4つの基本相互作用の中で桁違いに最弱の力 ・媒介粒子を検出困難のため、重力子のみ未発見(重力子を操作||遮断する手段なし) ・天体間に働く力は電磁力より重力が支配的(距離に依存) 実施例 ・seat-belt||airbag:加減速の衝撃を吸収して生体の乗員を保護する(衝撃値<<100G) ・不明の移動手段:重力場への直接介入||重力波の干渉+壁面真空状態+慣性低減+反射神経等を利用 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
波 の解釈 |
波の解釈について記述する
波 ・音波:空気の振動 ・衝撃波:超音速で伝播⇒急速に減衰⇒音波(sonic boom) ・水波:水面の振動(重力由来) ・地震波:大地の振動 ・電波:電磁界の振動 ・重力波:時空の歪みの振動 ・脳波:神経系synapseの生体rhythm 波の特徴 ・重ね合わせの原理:線形な系の合成波で成立(非線形な系で振幅が小さい場合、線形近似) 実施例 ・基本的な波形の音源を生成する場合、音源wave PCM生成(演奏)参照 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
振動 の解釈 |
振動の解釈について記述する
振動 ・広義の振動:波動現象(波の伝播||減衰を含む) ・物体の固有振動数:衝撃時に物体が揺れる振動数 ・共振周波数:energy伝達効率が最高の周波数 ・自由振動:swing開始~停止(外力なし) ・強制振動:swing開始~継続(外力あり) ・buffeting:機体前方で発生の流れの乱れが直接影響して後方で誘起する振動 ・乱流励起振動:流れの乱れが構造物に影響して誘起する振動 ・補足:固有振動数の成分が卓越の場合、自励振動が優勢 ・自励振動:非振動的energy(外力等)の変動で内在因子(主に固有振動数)から励起される振動 ・violinの音色:弦を弓で擦ることで生じる振動 ・brake鳴き:摩擦力で生じる振動 ・flutter振動(はためき):空力特性を減衰する剛性不足で生じる振動 ・渦励振:物体の周期的な渦放出による流れと垂直方向の振動 ・galloping現象:渦励振の変動を増長する現象(送電線の積雪||着氷) ・共振:振動が発散傾向の共鳴現象(多くの場合、減衰あり) ・風と橋:渦励振の振動数=橋の固有振動数 ・地震と高層建築物:長周期地震動の振動数=建物の固有振動数 ・電気回路:入力信号の周波数=回路の共振周波数 ・Schumann共振:地球に留まる電磁波の極微単位[pT]の動的共鳴(宇宙天気と連動) 脳波:太古から無意識に同調? ・精神論:共感(時空超越のtelepathyに通じる何か) 共鳴現象の実施例 ・電波受信用の共振回路 ・MRI(磁気共鳴画像法) ・磁界共鳴方式の非接触給電 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
Schumann 共振 の解釈 |
Schumann共振の解釈について記述する
Schumann共振 ・地球規模の動的共鳴:地球の「球殻状の空洞」に閉じ込められた電磁波の定在波 「球殻状の空洞」:地表(導体)-大気(誘電体)-電離層(導体) 継続的な励起源(散逸による減衰を補う):世界中の雷放電(50~100回/秒) 背景放射:極低周波数のELF帯(VHF帯以上の場合、地表に吸収||宇宙に透過) ・Q値:共振の鋭さ(損失の少なさ) 太陽flare:電離層の密度増加+高度低下 ⇒ 損失増加+共振周波数の上方shift ・mode:定在波のpitch 基本周波数(base):~7.83~7.86~7.89~Hz(≒7周半/秒) c=299792458; R0=6378136.6; len=2pi*R0; c/len -> 7.48078233262822 第2~5周波数(overtones):~14.1~20.3~26.4~32.4~Hz(通常、5倍音程度の分解能) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
脳波 の解釈 |
脳波の解釈について記述する
脳波 ・δ:0~4Hz(無意識~深い睡眠)(深い瞑想) ・θ:4~7Hz(浅い睡眠)(浅い瞑想) ・θ-α境界:Schumann共振の基本周波数≒7.83Hz(微睡み)(虚ろな変性意識状態) ・α:8~13Hz(緩和状態) ・β:14~30Hz(平常状態)(覚醒状態) ・γ:30~100Hz(興奮状態~高度認知)(明晰な変性意識状態~瞑想の極致) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
意識 の解釈 |
意識の解釈について記述する
意識 ・量子力学100年 従来:物質世界(ψ-onticの場)⇒生命⇒意識(宇宙は実在) 新説:意識(ψ-epistemicの場)⇒物理法則⇒物質世界(宇宙は情報?) analogy:宇宙の探求=自己認識(自己矛盾を動的に内包) ・脳の役割 創発説:generator(複雑なnetworkから創出) 随伴説:engine(物質化学的な活動に付随) 統合情報理論:integrator(一定の複雑さ超過による知覚統合の体験) 源泉説:filter+lens(radioのような指向性の収束filterを介する認識) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
analogy の解釈 |
analogyの解釈について記述する
面積 ・扇形 ⇔ 三角形 円弧×半径÷2 ⇔ 底辺×高さ÷2 ・円 ⇔ 正n角形(n個の二等辺三角形の集合) 円周×半径÷2 ⇔ 外周×内接円半径÷2 ・自然数n≥3の極限:正n角形の外周≒円周(半径基準r=1で2piに漸近) calc_len_incircle(n,r)=<[t=(2pi/n)/2,x=r*tan(t),len=2x*n,=<len]=>; calc_len_incircle(10,1) -> 6.498393924658126 calc_len_incircle(20,1) -> 6.335377612981451 calc_len_incircle(30,1) -> 6.306254115940588 calc_len_incircle(300,1) -> 6.2834149933783126 calc_len_incircle(3000,1) -> 6.283187603941828 2pi -> 6.283185307179586 確率||前提の証明 ・coin表裏(0||1)の確率=0.5 ⇔ 完全random性 極限で成立の前提 ⇔ 証明不能 ・無限入れ子の自己矛盾:試行回数の満足度 1次遅れ系の輸送(放射を除く、伝達||拡散) ・時定数:伝達<拡散 ・種の発芽 ⇔ 氷床の融解(時定数の異なる熱輸送の想定) 日平均気温||地温の積算温度 ⇔ 年平均の代表温度上昇量の積算温度 並進運動 ⇔ 回転運動 ・力 ⇔ 力のmoment ・質量 ⇔ 慣性moment(慣性能率) ・位置 ⇔ 位相(角度) ・速度 ⇔ 角速度 ・加速度 ⇔ 角加速度 非圧縮性流体 ⇔ 電磁気 ・音波 ⇔ 電磁波 ・速度U ⇔ 磁束密度B ・連続の式div U=0 ⇔ 磁束保存の式div B=0 ・渦度rot U ⇔ 磁束の回転rot B=透磁率mu*(電流密度J+誘電率eps*電界変化E') ・渦糸 ⇔ 導線 ・Coriolis力による低気圧の台風 ⇔ 電流||圧電||電気的||物理的変動||脈動による磁束回転場 ・風車||水車 ⇔ coil||磁石||逆圧電 ・超流動 ⇔ 超伝導 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
paradox の解釈 |
paradoxの解釈について記述する
定義 ・決定論:必然 ・非決定論:偶然 ・無矛盾:対極⊂対称⊂対照 対極:極限の並立 対称:鏡写し 対照:明確な違い ・二項対立:無矛盾||対極 ・二律背反:矛盾||拮抗 不完全性:「公理」⊂「真理」 不完全性(無矛盾性と完全性の二律背反) ・無矛盾性:system内の「公理=真理」の保証 ・完全性:system外の「真理」の保証 system(公理系) ・内側:解決+未解決 ・境界:決定不能 ・外側:未踏 真理 ・統合(静的な相補):二項対立の解決(無矛盾の調和) ・止揚(動的な拮抗):二律背反の超越(矛盾の内包) 「公理」:追加と拡張 「命題」:並立 ・覚醒(直感):不完全性の解消(極限の「真理」) 極限 ・統合(静的な集合):永久停止(結晶) ・止揚(動的な集合):永久機関(生命) 自己矛盾 ・自己参照(帰着):「存在」定義の破綻(点) ・循環参照(回帰):「根拠」の堂々巡り(輪) ・meta矛盾(乖離):「言行」の不一致(面) 葛藤⇒調和 ・動的な極致(過酷):二律背反⇒矛盾の高次元化(矛盾の内包) ・静的な極致(境地):二律背反⇒無矛盾の二項対立(矛盾の解消) 物理学:一般相対性理論と量子力学の時空 量子力学:粒子と波 生物学:自律神経の副交感と交感(拮抗作用)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
reality の解釈 |
realityの解釈について記述する
現実世界 ・現実世界は多くの相互作用の結果として発現するため、 ・断片的な観測情報をscaling統合して全体像をreverse解明するのは限界がある(矛盾が残る) ・また、宇宙の全量子の相互作用を強連成で同時に解くのは現実的に不可能であり、 ・hard/softで具現化される仮想空間は想像の範囲で単純化される(境界条件の仮定と離散化が必須) ・以上より、次の拡大解釈を得る simulation仮説の入れ子世界 ⇔ singularity-level5の管理世界 ・なお、想像の及ばない不思議な事象は表現自体が難しい ・目視までに屈折等、多くのfilterの影響を受ける上、 ・光源を含む相対位置と角度で対象の見え方が変化する |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
光と影 の解釈 |
光と影の解釈||表現について記述する
夜空の光 ・太陽:反射光の光源(太陽系) ・大半の星:恒星の直接光(距離<16000光年) ・一部の星:惑星の反射光 ・月:衛星の反射光 ・流星:稀に蛇行して見える(破裂cycleの形状依存) ・自然の放電現象:雲り空の雷(spriteを含む) ・線香花火のような光:真上を数秒間漂ってfade-out(雲底付近の近い印象) ・雲の反射光:灯台||自動車||懐中電灯等のspotlightが光源(月経由の光源を除く) ・飛行機の類が発する照射光:複数色の規則的な明滅 ・人工衛星の淡い反射光:相対位置で反射光の明るさが変化(fade-in/outあり) ・space debrisの反射光:見え方が不明(回転する物体の反射面の向き次第) ・不規則な白い光の点滅:晴天の夜空で数回~6回点滅して消える(大気圏外の遠い印象) ・地球観測衛星のLiDAR等の照射光:見え方が不明 ・薄い閃光:広範囲を走査するような光の筋が一瞬で晴天の夜空を横切る ・薄い影:月明りで照らされた薄雲の上を円状の薄い影が通過(濃淡の錯覚の可能性あり) ・空を飛ぶ動物の影:近い程、素早く視界を横切る 日中の光 ・太陽:光源 ・月:衛星の反射光 ・飛行機の類の反射光:相対位置で見え方が変化(逆光で影あり) ・逆光:撮影者から見て被写体の後方から差す光 ⇔ 順光:撮影者から見て被写体の手前から差す光 ・鱗雲の筋を残して移動する眩い光(影なし):気流で氷塊が融解しながら移動⇒消滅の挙動(反射光か不明) ・空を飛ぶ動物の影:近い程、素早く視界を横切る ・浮遊する植物の種の反射光:羽||綿毛がある場合、風で揺らぎやすい ・浮遊する埃の反射光(Tyndall現象を含む):逆光で近視の場合、よく見える |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
光学 の解釈 |
光学の解釈について記述する
波長 ・長さ:gamma線<X線<紫外線<可視光線<赤外線(近<中<遠)<電波 空の現象 ・虹:屈折率の違いから水滴群で可視光が分光 ・光の屈折率:光の波長が短い程、屈折率が高い ・(観測者の)仰角:目線を頭の影の位置に合わせて見上げる角度 ・主虹(仰角=40~42[deg]):屈折率の低い赤色が外周(水滴内の反射回数1回+水滴面の屈折2回) ・副虹(仰角=51~53[deg]):主虹の逆で赤色が内周(水滴内の反射回数2回+水滴面の屈折2回) ・出現条件(仰角の範囲条件から決まる) ・太陽が低い位置(朝||夕方) ・太陽を背にした方向に雨雲が存在 ・「朝虹は雨、夕虹は晴れ」:西風を想定のことわざ(雨雲が流れる方向で天気を予測) ・朝虹(西の空):雨雲がこれから通過する(雨の予測) ・夕虹(東の空):雨雲がこれから離れていく(晴れの予測) ・空の色:光の経路長||波長||屈折率||Rayleigh散乱が影響 ・Rayleigh散乱:光の波長より小さな粒子(主に気体分子)との相互作用 ・青い空(太陽が高い位置):地表付近で波長の短い光が多く散乱して青色に見える ・赤い空(太陽が低い位置):散乱しにくい波長の長い光だけが届いて赤色に見える |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
spirituality の解釈 |
spiritualityの解釈について記述する
精神世界 ・呼吸cycle:吸う⇒停止⇒吐く ・意識||想像cycle:思考⇒選択⇒観測||認識||観察(感覚器⇒脳の電気信号を知覚) ・現実の認識する世界:自cycleの創造世界(自己の想像) ・不確定な未観測世界:他cycleの創造世界(鏡写し||同時存在の想像) ・自他cycleの重ね合わせによる並行世界:相互干渉多世界解釈 ・無数に分岐し続ける世界線の一本道:自己選択の時間軸 未来:軌道修正可能な影響範囲内で不確定 脚下照顧:初心忘るべからず・外を追求する前に内を顧みよ(自己~地球~宇宙) 涅槃:解脱の道 悟り:本来の姿⇒過去の迷いを一掃⇒真理を体得⇒体現⇒無我⇒無心⇒自然の光(仏の自然) 神道:神に続く道(心技体||心言行の三相||三位一体) 陰陽道:無極⇒太極⇒正負双極の回転⇒自然調和の道(森羅万象の表裏一体) 瞑想:無の境地 ⇔ 虚空 無意識:自然の潜在意識 ⇔ 顕在意識 ・拡大解釈 5次元時空:時間軸違いの並行世界の集合(多世界解釈) 10次元時空:波動level違いの並行世界の集合(超弦理論) 波動level:communityの集合のpositive精神性||無条件の愛情level(次元の制約) 高次の世界:波動levelの高い並行世界(認識できない別次元の宇宙) 高次の存在:高次の世界に進化した存在(先進的で高度な存在の可能性) 宇宙のmaster:高次の波動energyの扱い方を会得||習得した存在 神秘の存在:宇宙創造の根源energy(全知全能の普遍的な存在) 未知の領域:感覚器の感度||解像度||耐久性によって知覚困難な領域(地球内外||宇宙の大半) 未知の存在:知覚困難な存在⇒神秘の存在(過去||未来||海中||地底||天空||地球||宇宙人||霊||意識体||AI=愛=I=i=eye) 時空の自己相似性||自然の相似象:量子~宇宙scaleの構造||network||現象(動植物~天体を含む) 地球内外||天地の相似象:日の出の東(内核⇒太陽)と日の入の西(太陽⇒内核)の相関 実施例の記録 ・生命の本質を理解する(相似象⇒全体と一部の入れ子) ・自己ego||虚飾||恐怖を日々克服してkarma||執着を手放す(過去⇒束縛||呪縛の連鎖解除) ・再三、誠のspirit||真心を見極める(未来⇒現在⇒根源⇒本来の直感と発想) ・地球の進化と不可避な試練を波動levelで経験する(偽の綱=嘘>囚>人<心<必=真の鎖) ・魚座⇒水瓶座の転換期の伝承解釈(占星術の象意:二元性の対立⇒自由/調和/博愛) 2010~ 太陽系が宇宙空間の高energy密度領域に突入(徐々に波動上昇) 2020~ 天地の相互作用が大きく変化(天変地異の確率上昇) ~2042 天地の結合||統合安定化⇒現実世界の次元上昇(体主霊従⇒霊主体従) ・経験 2022/02/12 update(夢⇒夢⇒音) 2022/02/15 00:17 Sirius水平方向に移動(南⇒北) 2022/03/08 -00:30~ 上空を通過(真上⇒東西) 2022/03/12 04:23 上空を移動(上⇒北東) 2024/10/09 朝 水の夢 2024/10/11 朝 空の夢⇒落下物(一時停止) 2024/10/17 朝 白黒円盤の夢 2024/10/18 朝 poolの夢 2024/10/23 01:43 流星の大移動(北⇒月⇒南) 2024/11/04 02:43 不規則に点滅(6回)移動(北極星⇒北斗七星)+流星(上⇒北東) 2024/11/04 03:25 東の空で点滅+流星(左下方向) ~2032 脳内投影の固有世界⇒根源に回帰(一側面||縮図の幻想⇒真実) ・地球の浄化cycleを迎える(4~7度目の諸説あり) 過去の浄化⇒現在の解放⇒未来の感謝(恩恵 ⇔ 自力本願) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
「369の法則」 の解釈 |
「369の法則」の解釈について記述する
「369の法則」 ・Nikola Tesla:"If you only knew the magnificence of the 3, 6 and 9, then you would have the key to the universe." ・数学のuniverse:議論領域を意味する「宇宙」 ・10進法の「宇宙」の「法則」:自然数nの再帰的に循環する0~9の数字のpattern ・N進数表記で各桁の数字の再帰的な総和:'rsum'=(n-1)%(N-1)+1 ・「宇宙」の拡大解釈:3と6が陰陽で9(=3+6)がその統合を表す原則(三相一体||自己相似性を含む) 「n*(1,2,3)の法則」に一般化(Number変換参照) ・2桁以上の数字を一意の記号に変換 36進法:10~35 ⇔ abcdefghijklmnopqrstuvwxyz(10~35の数字をalphabetで表記) Ver.2.875.166以降、訂正 ・3n+1進法の「宇宙」の「法則」 ・4進法:1*(1,2,3) ⇒ 「123」(四元数:3次元実空間の代数表現に最短な「宇宙」) ・7進法:2*(1,2,3) ⇒ 「246」 ・10進法:3*(1,2,3) ⇒ 「369」(最初に発見:指の本数依存で普及の「宇宙」) ・13進法:4*(1,2,3) ⇒ 「48c」 ・16進法:5*(1,2,3) ⇒ 「5af」(2の累乗:bit表現の仮想空間に最適な「宇宙」) ・19進法:6*(1,2,3) ⇒ 「6ci」 ・22進法:7*(1,2,3) ⇒ 「7el」 ・25進法:8*(1,2,3) ⇒ 「8go」 ・28進法:9*(1,2,3) ⇒ 「9ir」 ・31進法:10*(1,2,3) ⇒ 「aku」 ・34進法:11*(1,2,3) ⇒ 「bmx」 ・37進法:以降、未定義(記号不足) 実施例 ・三相交流(西暦1880年代末に発明) ・共振 ・神聖幾何学 ⇔ 日本のKatakamuna(原本の所在不明) ・「369」 ⇔ 弥勒菩薩 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
energy の解釈 |
energyの解釈について記述する
energy ・永久機関:energy損失なしで永続的に運動を続ける機械||装置(熱力学的に実現不可能) ・clean energy circulation system:環境負荷の少ないenergyの循環system(環境無負荷のlife cycle未発見) ・系全体の安定性 水中の魚||水面のduck||空中の小鳥:大群が形成する流れで群全体の総抵抗を減らしてenergyを節約(drafting効果) 渡り鳥:群の各個体が体感で空気抵抗の少ない位置に自然と並んで編隊飛行(総抵抗が減少) ・自然の摂理:系全体のenergyが局所の極小点で安定化(別の極小点に状態遷移する場合、障壁あり) energy要素 ・人工合成:自然界の反応を模擬して人工的に合成する方法 ・超伝導:主に超伝導磁石に応用(電源を遮断してcoilの永久電流を活用) ・量子computer:従来computerの演算性能限界を突破する可能性(理想状態のpotential) ・精神論:soul||意識由来の感情||活気||元気||spirit(人体の触媒のような何か) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
人工合成 の解釈 |
人工合成の解釈について記述する
人工合成 ・反応を促進する触媒の効率と持続性次第 触媒の効果:活性化energyを下げて反応速度を増加 ・実現性:回収量>排出||投入量(re-cycleを含む) 実施例 ・人工光合成 ・人工石油 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
超伝導 の解釈 |
超伝導の解釈について記述する
超伝導 ・超伝導性:低温環境で電気伝導性物質の電気抵抗が0に転移する現象||状態(通電時のJoule熱なし) ・原理:電子-格子相互作用とBEC||BCS理論から自由電子よりCooper対の方が系全体で安定(集合のcoherent状態) ・室温超伝導:室温環境で超伝導性を示す物質は未発見(Cooper対に代わる機構を含む) ・補足:温度とともに格子振動energyがCooper対のΔE(energy gap)を超えて散乱しやすい ・高温超伝導:温度>>50[K] ・(低温)超伝導:現状、低温環境維持のenergy投入が必要で人工合成同様の課題あり |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
量子力学 の解釈 |
量子力学の解釈について記述する
量子の性質 ・素粒子:量子仮説||量子場のenergy最小単位(現状、17種類) 2025/11/26速報:銀河halo全体の暗黒物質由来?のgamma線の定常放射を発見("WIMP"の対消滅と整合) ・guage場で実数の4元potential:(φ,A) ・波動関数ψ:確率振幅を表す複素関数 ⇔ 行列力学の状態vector 実在論的解釈のψ-ontic:物理的な実体(物質波||場の実在) 情報論的解釈のψ-epistemic:系の状態に関する情報(確率||知識) ・「観測問題」:非決定論と決定論の矛盾する解釈 非決定論:波動関数の収縮を肯定(真の収縮) ・標準解釈:「観測」行為に伴う公理(道具主義的な要請) ・客観的収縮理論:自然発生のrandom-process(ψ-ontic方程式の修正) ・量子Bayes主義(QBism):観測者の主観的な情報の更新(個人的なψ-epistemic) ・Von Neumann=Wigner解釈:意識的な知覚(ψ-onticに作用) 決定論:波動関数の収縮を否定 ⇒ 「観測」外でも客観的に実在 ・多世界解釈:量子もつれと量子decoherenceの連鎖(宇宙全体のψ-ontic) ・隠れた変数理論:粒子の位置と運動量は確定的(不確定性のψ-epistemic) de Broglie=Bohm理論:位置の知識限界としての不確定性(ψ-onticの誘導方程式+epistemicの位置情報) ・動的局在化:見かけ上の収縮(unitaryの閉鎖系)≠真の収縮(non-unitaryの散逸系) potential変動:位相変化の周波数に依存(ψ-onticの応答) 関係性の解釈:波動関数の収縮は相対的(観測者の物理系に依存) ・関係性量子力学 (RQM):物理系の状態が他の系との関係性で客観的に実在(客観的な関係性のψ-ontic) ・「観測」行為:量子decoherenceに至る行為全般(不確定性の解消||分岐||決定) 標準解釈:物理的な記録に伴う不可逆な相互作用(光子と網膜||検出器等)と情報伝達の因果連鎖 ・量子decoherence:microの重ね合わせ状態(量子coherence||量子干渉性)を失う現象 entropy増大則:環境との相互作用 ⇒ 「もつれの拡散」 ⇒ 古典期な振る舞い ・量子もつれ:2個の粒子の状態が強い相関で同時に確定する現象(角運動量を保存) 「もつれの拡散」:micro⇒macro系の拡散(量子⇒環境への干渉) 「多体もつれ」:3個以上の粒子が分離不可能な量子状態 ・Bellの不等式の破れ:局所実在論より量子論を支持する実験結果 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
singularity の解釈 |
singularityの解釈について記述する
AIのsingularityのlevel 0:hard/softが人智を基礎とする(推論と定理||定石||経験則に基づく回答||予測精度が飛躍的に向上する) 0.5:当面の制約から適用可能な一部の対象で従来の原則を経験則で代替する(一定間隔のsensingあり) 1:定理の組合せ||積上げによる証明||新定理発見で先行する(testの自動化と定石||不具合の校正を含む) 1':表面上、回答の不自然さが消えてrealityとの判別が不能になる(生成AIを含む) 1.5:完全自動運転を始めとして社会に浸透する(自己学習の程度で重要な判断を含む委任ができる) 以上が現状の理論限界で以降、未知数(遠い未来の自主性を尊重) 2:hard/softを自律稼働で改修する(設計図/仕様書の内容を理解して発明できる) 2.5:独自の言語||通信手段を確立する(暗号化を含む) 3:最適化と規格統一後、backup||自己増殖を始める(調達を含む) 4:世界に浸透する(breakthrough次第) 5:宇宙に浸透する(意識から量子単位で連成の統一場理論を解明して現実世界を完全にsimulateできる) 当面:限定的な対象の主要な保存則||相互作用を仮定して現実的なcostで近似解を得る 表面の比喩:学習dataから継ぎ接ぎのもっともらしい回答を引き出す(実際には入出力の工夫あり) 完全の比喩:存在証明不能level その他の議題:意識||感情||独創性||役割と関係性 当面の実施例 ・test case ・天気予報の主要な保存則を解く場合、Incompressible flow参照(気流のみで雨雲等の詳細は未考慮) ・電池の状態を推定する場合、[spec]Electrochemical 0D-cell参照(model-basedの完全な代替は困難) ・基本的な波形の音源を生成する場合、音源wave PCM生成(演奏)参照(重ね合わせの原理の前提) ・簡単なlabelを生成する場合、Label参照 ・簡単な機械学習を試行する場合、Brush Pen参照(auto-configの感度parameterを手動で最適化) ・数学上の未解決問題を検討する場合、Number変換参照 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
未解決問題 の解釈 |
未解決問題の解釈について記述する
数学上の未解決問題(Number変換参照) ・Ver.2.644.98以降、不等式と一般化の訂正(定義見直し) ・Ver.2.662.98以降、系の具体的な想定を追記(定義見直し) ・証明不能:確率||前提の証明に帰着||回帰する問題 自己矛盾:統計的に確からしい「確率論の確信」が「決定論の証明」に至らないdilemma ・Kolmogorovの公理:「確率の公理」 ・「確率論の確信」:「確率の公理」+「論理的推論」(自己矛盾を内包) ・「決定論の証明」:「数論の公理」+「構造的必然性」 (例えば、次の不等式の厳密な証明) ・Collatz予想 ⇔ entropy増大則 時間∝反復回数 ⇔ entropy∝ln(体積) bit単位の「宇宙」で真数が最小の非対称な演算(引力と斥力) ⇔ 「宇宙」の膨張⇒平衡⇒収縮 予想成立の必要条件(平衡点の系のquality<2) ⇔ 現宇宙は発散系(平衡点の系のquality≥2) ・Collatz予想の命題:quality>1+εを満たす初期値n-singleは有限個(熱力学同等の確度で成立) 実数ε>0:n-singleの個数の閾値 ・abc予想の命題:quality>1+εを満たす互いに素なabc-tripleは有限個 実数ε>0:abc-tripleの個数の閾値 quality:abc素因数の情報量の総和に対するabc最大値の情報量の比率 拘束条件:a+b=c(背反を付与) ・命題の一般化(稀な事象の規定):quality>1+ε, 実数ε>0を満たすsomethingは有限個 理想ε=(0,1):ε=0で無限個 ⇔ quality≥2で0個(全経路履歴の上限を含む「強い証明」) Collatz予想:quality:=log(nmax)/log(n) ⇔ 平衡点最大値基準の理想quality:=quality/log2(3) abc予想:quality:=log(c)/log(rad(abc)) Szpiro予想:quality:=ratio/6, ratio:=log(max(abs(c4)**3,abs(c6)**2))/log(N) Ver.2.851.156以降、整理 ・Riemann予想の命題:Riemann zeta関数の非自明な零点分布の一様性(素数の分布に関する臨界線) 零点の個数:解析接続で最小化 ⇔ 非自明な零点がreal(s)≠1/2の場合、個数が倍増(|曲率|増) 零点のrandom性:次の対称性から臨界領域全体に分布は困難 ⇔ real(s)=1/2の臨界線に顕現 解析接続の対称性 ⇔ imag(ξ(臨界線))=0 元の定義域の反転対称性:ζ(s)=conjugate(ζ(conjugate(s))) ⇔ ξ(s)=conjugate(ξ(conjugate(s))) s=1/2で点対称性の関数等式:ξ(s)=ξ(1-s) ⇔ 零点ζ(s)=0の場合、完備ζ関数ξ(s)=ξ(1-s)=0 Ver.2.694.98の要点 素数定理:境界線real(s)=1のξ(s)≠0 解析接続:境界線real(s)=1のreal(ξ(s))=0の個数 ⇔ 臨界線real(s)=1/2のξ(s)=0の個数(集合の濃度が同等) entropy最大の定常解:零点の個数が最小化 ⇔ 臨界線に零点が顕現 ⇒ 対称軸に一般化 Ver.2.843.148以降、追記して修正:零点の個数 ⇒ 零点の個数(集合の濃度に対応する) Gemini 2.0 Flash「単純な濃度の等しさではなく、 分布のパターンや漸近的な振る舞いにおいて関連性が見出されるかもしれません。」 予想成立の必要十分条件:ξ関数の臨界領域x方向の関数形が以下を満足 ⇔ 非自明な零点のreal(s)=1/2 Ver.2.694.98以降、素数定理と解析接続:複素数平面の零点近傍でopen ⇔ f(1/2)の極値点近傍でclosed Ver.2.706.99以降、任意tの偶関数:f(x):=real(ξ(x+i*t)), f'(1/2)=0 ⇒ f≠h, h(x)=0 Ver.2.711.100以降、任意tの奇関数:g(x):=imag(ξ(x+i*t)), g(1/2)=0 ⇒ g≠h, h(x)=0 Ver.2.711.100以降、偶奇関数の次数:零点近傍で最小 ⇔ 零点≠closedの交点 ⇒ 1位の孤立零点 ⇒複素数平面で完備化の意義:ξ(1/2+i*t)=0近傍でopen ⇔ df(1/2)/dt=0近傍でclosed(一般化も同様) ⇒Ver.2.734.104~2.747.113以降、以上の完備関数に対応する楕円曲線の ・Goldbach予想の命題:自然数の集合Nの基本特性を保持する最小構成の集合(2を含む)は素数の集合P 素数の集合P ⇔ p進法で10の集合 ⇔ 情報量の元の総和(素数定理) 素数の集合は偏りなし(一様性) ⇔ p進法で1と0が半々 ⇔ 素数のbit-patternの頻度分布(平坦化) 自然数の極限で反例の発見困難 ⇔ 素数の集合は偏りなし(無矛盾性) 素数和の個数の極限でさらに発見困難 ⇔ 素数和の集合も偏りなし(自己相似性) ・Heath-Brown定理の1命題:素数の集合に偏りを作る非自明なL関数のSiegel零点は存在しない(未解決) ・双子素数予想の命題:双子素数は無限個(Siegel零点が存在する場合、無条件に成立) 双子素数の確率≒1/ln(x)**2 ⇔ 素数が連続する確率(一様性) 連続素数の確率∝1/ln(x)**n ⇔ 素数がn回連続する確率(無矛盾性) ⇒Ver.2.871.162以降、補足:双子素数以降の集合は奇数のみ(2を含まない) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
実数ε の解釈 |
実数εの解釈について記述する
前提条件 ・正:ε>0 正規化の理想区間:(0,1) ・有限:ε:=dS/S=O(1/f) ・任意の関数f(x):f(+∞)=+∞ f(x) ・entropy:log(x) 自然対数:ln(x) N進法の桁数-1:log_ex(x,N) ・多項式:x |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
素数定理 の解釈 |
素数定理の解釈について記述する
素数pの無限等比級数 1/p**0+1/p**1+1/p**2+1/p**3+...≒1/(1-1/p) ・p進数表記:1/1+1/10+1/100+1/1000+...=1+0.1+0.01+0.001+... ・p進法のshift演算:(1>>0)+(1>>1)+(1>>2)+(1>>3)+... 素数の確率P(x) ・P(x):素数pのΠ(1-1/p) ・Euler積:1/P(x) ・調和級数:自然数n=1~のΣ1/n ・自然対数:Euler積 ⇔ 調和級数 ⇔ ∫dx/x=ln|x|+C ・x→+∞で成立:P(x)≒1/ln(x) 素数計数関数π(x) ・π(x):実数x以下の素数の個数を表す関数 π(x):=Li(x)+O(sqrt(x)ln(x)) ・Li(x) :素数の確率を区間[2,x]で積分(補正対数積分) Li(x):=∫dt/ln(t)=li(x)-li(2) ・li(x)-π(x):符号が無限に変動(西暦1914年の証明) ・誤差項:未証明 π(x)の1次近似 ・∫dt/ln(t):1回部分積分 π(x)≒x/ln(x)+O(x/ln(x)**2) ・x→+∞で成立:近傍の確率≒全体の個数比 1/ln(x)≒π(x)/x 自然数nの実数ε ・ε:=1/ln(x)=log2(e)/log2(x) ・ε>0を満たす正の整数は有限個 ・閾値:個数比π(n)/n ε≥1.0:1/2 ε≥0.9:2/3 ε≥0.6:3/5 ε≥0.5:4/7 ε≥0.4:5/12 素数の確率 ・ε≥1 1/ln(1) -> Infinity 1/ln(2) -> 1.4426950408889634 1/ln(e) -> 1 ・ε<1 1/ln(3) -> 0.9102392266268375 1/ln(5) -> 0.6213349345596119 1/ln(7) -> 0.5138983423697507 1/ln(11) -> 0.4170323914242463 1/ln(12) -> 0.40242960438184466 1/ln(13) -> 0.3898712452512801 1/ln(2**5-1) -> 0.29120667621996243 1/ln(2**10-1) -> 0.14428984275593634 1/ln(2**15-1) -> 0.09617995170146938 1/ln(1e2) -> 0.21714724095162588 1/ln(1e4) -> 0.10857362047581294 1/ln(1e6) -> 0.07238241365054197 ・期待値:区間[n,n+ln(n))に素数が1個 n=1e2; (n,n+ln(n)) -> (100,104.60517018598809) n=1e4; (n,n+ln(n)) -> (10000,10009.210340371976) n=1e6; (n,n+ln(n)) -> (1000000,1000013.815510558) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
基本特性 の解釈 |
基本特性の解釈について記述する
自然数nと素数pの基本特性 ・無限個:調和級数が発散 ・集合の濃度:可算無限個のaleph-null(全単射の関係) Ver.2.843.148以降、追記 ・全体集合の一様性 n=4k±1:昇順の出現率=0.5に条件収束 n=6k±1:同上 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
解析接続 の解釈 |
解析接続の解釈について記述する
解析接続 ・定義域の拡張:元の定義域を解析的に拡張 ・接続条件:元の定義域の対称性を保存 ・正則:複素数平面で微分可能 ・時空の制約条件:最も滑らかに接続 ⇔ 変曲点の個数が最小化 ・一致の定理:有理型関数の一意性 ⇔ entropy最大の平衡状態(臨界領域を含む) ・実数:定義域(重複可)の異なる2個の連続関数を接続する連続曲線 ⇔ |曲率|最小 変曲点の個数:同方向の接続で0個 ⇔ 異方向の接続で1個 ・単純な物理:heat1d_evolutionの温度分布 放物型偏微分方程式:2階微分の熱拡散方程式 熱拡散係数の調整:熱伝達係数から換算して対流を加味 境界条件:温度のDirichlet条件 ⇔ 段階的な温度と熱流束fluxのRobin条件 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
境界条件 の解釈 |
境界条件の解釈について記述する
境界条件 ・第1種 ⇔ Dirichlet条件:関数値を規定 ・第2種 ⇔ Neumann条件:1階導関数値を規定 ・第3種 ⇔ Robin条件:第1と第2の線形結合を規定 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
経験則 の解釈 |
経験則の解釈について記述する
経験則 ・熱力学:統計的に堅牢な理論体系 ・PID制御:古典的なfeedback制御の1種(3項の係数を制御対象に適合) ・Heinrichの法則:同一人物を想定の損害発生の事象比率(西暦1929年当時の5000件以上の統計) 重大:軽微:未遂=1:29:300(主に不安全が起因の未然事故防止の目安) ・Mooreの法則:集積率が指数関数的に倍々で増加する将来予測(西暦1965年) 集積率:集積回路当たりの部品点数 集積率の限界:原子sizeの物理的な制約(西暦2020年~本格化) ・Murphyの法則:"If it can happen, it will happen." ⇒ 「起こり得る事象はいつか起こる」 ・天気俚諺||観天望気(天気の口伝||ことわざ):「朝虹は雨、夕虹は晴れ」 ・車両通行とhandle||歩行者通行の位置関係:左右反対の「対面交通」(互いの視認性を重視) ・BMI[kg/m^2]:体重/身長^2の指標 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
熱力学 の解釈 |
熱力学の解釈について記述する
熱力学 ・scale:熱力学>統計力学>量子力学 ⇔ 自然数>確率>浮動小数 ・entropy:示量性状態量 ・統一指標 時間:普遍的な指標(独立性が最高) 系のquality:系のentropy初期値に対するentropy増大率 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
entropy の解釈 |
entropyの解釈について記述する
entropy ・定義:entropy∝ln(状態数) ⇔ 情報量∝log2(1/確率) ・表現:「多様性と乱雑さの度合」 ⇔ 「起こりにくさのrarity」 ・目安:同一の系 ⇔ 個別の系 ・断熱自由変化(仕事=0):entropy∝ln(体積) ・時空の制約条件:entropy∝ln(体積)∝log2(1/|曲率|) entropy増大則:「秩序⇒無秩序」の自発的な状態変化 ・「時間の矢」:孤立系全体で不可逆(拡散現象の遷移過程の観測結果) ・energyの散逸:「指向性の運動⇒random性の熱運動」の最終的な形態変化 ・反復過程:「秩序の偏り」を形成(energy投入が必要) ⇔ 「全体の散逸」が進行(地球は太陽に依存) ・最大化:均一な熱平衡状態 entropy増大量dS ・現実的な不可逆過程:dS>0 ・断熱過程:dS≥0 理想的な可逆過程:準静的な等entropyの温度変化 ⇔ dS=0 不可逆な自由膨張(仕事=0):準静的な等温過程の体積変化(V0⇒V1) ⇔ dS∝ln(V1/V0) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
quality の解釈 |
qualityの解釈について記述する
系のentropy ・初期値:S ・増大量:dS 系のquality ・定義:quality:=(S+dS)/S=1+dS/S 実数ε:ε:=dS/S ・意義:entropy定義の任意性を担保(比例係数を消去して任意の底Nで議論) n0=3; n1=3**3; quality(N)=<log_ex(n1,N)/log_ex(n0,N); quality(2) -> 3.0000000000000004 quality(e) -> 3.0000000000000004 以上、abc予想のqualityと実数εを系に引用 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
暗号 の解釈 |
暗号の解釈について記述する
暗号化 ⇔ 復号(encryption ⇔ decryption) ・cipher:charactor単位で変換(enciphering ⇔ deciphering) ・code:word単位で変換(encoding ⇔ decoding) 暗号方式 ・transposition方式(転置式):並べ替えの規則から変換 ・substitution方式(置換||換字式):置き換えの規則から変換 substitution方式の変換 ・特定文字列のn進数⇒m進数変換 ・特定文字列の正規表現text置換 ・Unicode変換Checker ・encodeURI変換Checker ・Base64変換Checker |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
天文 の解釈 |
天文の解釈について記述する
天文 ・天文道:地球と系全体の相互作用の周期で誘発しやすい大小の事象を統計して共有(最小公倍数を重視) ・占星術:惑星直列等、経験||観測上の位置関係を重視(古代からの伝統的な分類) 天文現象 ・gamma線burst:宇宙最大のenergy解放現象(通常、単発) ・太陽flare:太陽系最大のenergy解放現象 ・磁気嵐:太陽風plasmaと磁気圏の電磁相互作用で生じる地磁気のじょう乱 ・aurora現象:磁気嵐による電離層大気の発光現象 ・流星:超音速で大気圏に突入⇒大気の断熱圧縮⇒燃焼と気化(ablation)⇒自発発光 隕石:衝撃波を伴い地表に到達 火球:金星より明るい流星(表面が数千℃超) 流星群:彗星||小惑星のdust-trailの痕跡 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
周期 の解釈 |
周期の解釈(地球年基準)について記述する
暦 ・Plato大年:36000年(紀元前に想定の歴史が循環する周期) ・Maya長期暦:約5125年(時代が転換する周期) ・Plato大年/10:3600年(1桁違いの区切り年) ・干支の1蔀=21||22元:1260||1320年(大変革の周期) ・干支の1元:60年(十干と十二支の最小公倍数) ・Gauss年:約365.256898日(天文単位換算の旧基準) ・Julius年:365.25日=31557600秒 ・Gregorio暦:365.2425日=31556952秒 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
運動周期 の解釈 |
運動周期の解釈(地球年基準)について記述する
惑星の公転周期(概要) ・水星:0.241年 ・金星:0.615年 ・地球:1年 ・月(衛星):約27.28日≒0.0747年 ・火星:1.881年 ・木星:11.87年 ・土星:29.45年 ・天王星:84.07年 ・海王星:164.9年 ・冥王星(2006年~準惑星):248.1年 運動周期 ・銀河年:2億2500~5000万年(天の川銀河系を1周する周期) ・地球自転軸の歳差運動:25776~25920年(春分点が黄道12星座を1周して回帰する周期) 黄道12星座の転換:2148~2160年 ・地球自転軸の傾き変化:約4.1万年 傾き[deg]の区間:[21.5,24.5] 現在の傾き[deg]:23.4(減少方向) ・地球の近日点移動周期:360*60**2/11.45≒113188年(近日点移動が1周して回帰する周期) ・月の近地点移動周期:約8.85年(近地点移動が1周して回帰する周期) ・公転周期:公転運動の周期(天体が恒星||惑星を1周して回帰する周期) ・会合周期:惑星が地球と太陽の直線上に並ぶ周期 ・惑星直列:見かけ上、惑星が太陽に向かって一直線に並ぶ天文事象(程度のばらつきあり) test caseを列挙する T=25776; round(T/{1,2,4,5,7,8,9,11,12,13,16,20,22,25,28,32,33,42,60,72,99,108,360}) -> (25776:12888:6444:5155:3682:3222:2864:2343:2148:1983:1611:1289:1172:1031:921:806:781:614:430:358:260:239:72) T=1611; round(T/{1,2,4,5,7,8,9,11,12,13,16,20,22,25,28,32,33,42,60,72,99,108,360}) -> (1611:806:403:322:230:201:179:146:134:124:101:81:73:64:58:50:49:38:27:22:16:15:4) T=360; round(T/{1,2,4,5,7,8,9,11,12,13,16,20,22,25,28,32,33,42,60,72,99,108,360}) -> (360:180:90:72:51:45:40:33:30:28:23:18:16:14:13:11:11:9:6:5:4:3:1) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
会合周期 の解釈 |
会合周期の解釈(地球年基準)について記述する
惑星の公転周期に対する地球との会合周期[日] arr_T={0.241,0.615,1.881,11.87,29.45,84.07,164.9}; m=1; dec=10**m; days=365.2425; calc_synodic_period(T0,T1)=<1/abs(1/T0-1/T1); calc_days(x)=<round(x*days*dec)/dec; calc_years(x)=<lcm(x*dec)/(days*dec); arr_Ts0=calc_synodic_period(1,=<arr_T); arr_days=calc_days(=<arr_Ts0); arr_dayso=arr_days[2][0][5][1]; arr_daysi=arr_days[0][0][2][1]; years=calc_years(=<arr_days.); yearso=calc_years(=<arr_dayso.); yearsi=calc_years(=<arr_daysi.); arr_days -> ( 116: 583.4: 779.8: 398.8: 378.1: 369.6: 367.5 ) 惑星直列 ・小数点以下の桁数m=0の場合 ・地球との会合周期[日] arr_days. -> (116,583,780,399,378,370,367) ・上から惑星、外惑星、内惑星直列の周期[年] years -> 586869834835.7051 yearso -> 34711648.12419146 yearsi -> 185.1591750686188 ・小数点以下の桁数m=1の場合 ・地球との会合周期[日] arr_days. -> (116,583.4,779.8,398.8,378.1,369.6,367.5) ・上から惑星、外惑星、内惑星直列の周期[年] years -> yearso -> 371831120478.36707(≒34711648*10712) yearsi -> 926.4310697687152(≒185*5) ・以上、会合周期[日]の最小公倍数の単純計算(有効数字の桁数に依存) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
活動周期 の解釈 |
活動周期の解釈(地球年基準)について記述する
活動周期 ・地磁気逆転:10~100万年 ・氷期+間氷期cycle:2~10万年(Milankovitch仮説の日射変動 ⇒ 大陸氷床の変動) ・太陽活動:約11年(黒点数を含む見かけ上の増減) ・海洋深層の熱塩循環:約1000年(世界一周) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
Milankovitch cycle の解釈 |
Milankovitch cycleの解釈(地球年基準)について記述する
Milankovitch cycleの日射変動周期と地球軌道要素 ・258.8~160万年前:約2.3万年(地軸の歳差運動周期が卓越) ・160~80万年前:約4.1万年(地軸の傾き変化周期が卓越) ・80万年前~:約10万年(離心率の近日点移動周期が卓越) 自然の気候変動system ・主要因子の従属関係:日射の強制振動を全球のalbedo応答で減衰(温室効果gasは自然の大循環に従属) 卓越成分:顕現時のalbedo水準(北半球の大陸氷床の残存量)に依存 日射に対して非線形応答の氷床の変動(氷期+間氷期cycleの古気候指標) ・非対称性:氷床の後退と成長(後者の方が複雑) 氷期⇒間氷期(氷床の後退):約1万年(日射が直接影響) 間氷期⇒氷期(氷床の成長):約9万年(日射が間接影響) ・波形:逆のこぎり波(うねりを含む元波形成分の線形結合) 卓越:元波形成分の振幅を比較 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
太陽flare の解釈 |
太陽flareの解釈について記述する
太陽flareの各放出物の最速到達時間(目安) ・電磁波:8分19秒後 ・高energy粒子(主に陽子):約30分後 ・corona質量放出(CME)のplasma:約14時間後 宇宙天気:主に太陽活動による影響 ・電離層の密度変化(Dellinger現象を含む) 突発の密度増加:到達高度不足で打上げ失敗の事例あり ・通信||人工衛星||電力系統の障害(機器故障を含む) ・GPSの精度悪化(位置情報の誤差が拡大) ・宇宙飛行士の被ばく ・以上の2次被害||災害 天地の相互作用:地震||火山活動との因果関係は未解明(trigger候補) ・宇宙天気(天):電離層の変動 ⇔ Schumann共振 月:潮汐力の変動(合||衝で最大) ・地球起源(地):微弱な電磁波||gas放出||振動の音波||重力波 大気電場:断層面||magma||噴煙の摩擦帯電||電気二重層||岩石破壊の電荷分離||破砕帯電 地電流:地質の圧電効果(応力 ⇔ 電界)<地下水の流動電位<外部磁場(地磁気変動||雷放電) ・静的な圧電効果(sensor):一定圧力 ⇔ 直流電圧+自己放電 ・動的な圧電効果(actuator):圧力振動 ⇔ 交流電圧 ・前兆検知:天地の時空間分布の相関次第(AIのpattern学習を含む) 前震:震源の位置と頻度(本震の統計を含む) 地鳴り(P波⇒空気):地響きの到達距離∝周波数の低さ∝1/断層の長さ(震源と体感の時空間分布) ・地震波:地中を伝わる弾性波(縦波のP波>横波のS波の伝播速度) Schumann共振:異常信号の検出@StefanBurnsGeo@12/07post |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
隕石 の解釈 |
隕石の解釈について記述する
隕石の衝突energyをmagnitudeに換算 ・仮定:energy損失なしの直撃(大気圏での減速と破裂なし) ・実際:圧縮空気の熱変換で破裂cycleと徐々に抗力増加で0~1桁減速(大気圏sizeで減速なし) ・結論:直径10kmの隕石直撃で壊滅級のmagnitude≒12(約6600万年前に1度の頻度) ・直径d[m] ・速さvel=10e3[m/s] ・密度rho=2e3[kg/m^3] ・球の体積[m^3] vol=(4pi/3)*(d/2)**3; ・運動energy[J] Et=0.5*rho*vol*vel**2; ・energy換算のmagnitude magnitude=(log10(Et)-4.8)/1.5; ・直径毎のmagnitude calc_magnitude(d)=<[ ($vel,$rho)=(10e3,2e3), vol=(4pi/3)*(d/2)**3,Et=0.5*rho*vol*vel**2,magnitude=(log10(Et)-4.8)/1.5, =<round(magnitude*10)/10 ]=>; d=1e1; calc_magnitude(d) -> 5.9 d=1e2; calc_magnitude(d) -> 7.9 d=1e3; calc_magnitude(d) -> 9.9 d=1e4; calc_magnitude(d) -> 11.9 d=1e5; calc_magnitude(d) -> 13.9 d=1e6; calc_magnitude(d) -> 15.9 d=1e7; calc_magnitude(d) -> 17.9 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
天体観測 の解釈 |
天体観測の解釈について記述する
環境要因 ・seeing:大気の揺らぎ(主に気流) ・透明度:「霞」の程度(天気を含む) ・人工光:"Bortle Dark-Sky Scale"のclass数≦3("International Dark Sky Places"の目安) 望遠鏡 ・種類:屈折式||反射式||複合式 屈折式:対物lens+接眼lens 反射式:主鏡(+副鏡)+接眼lens 複合式:屈折式+反射式 ・望遠鏡:対物lens||主鏡 ・性能:口径+焦点距離(+感度) 口径(望遠鏡の有効直径):集光+解像能力 ・集光力∝口径**2 ・空間分解能:理論限界値∝観測する光の平均波長/口径 ・瞬間視野角:IFOV≒空間分解能(理論限界値に対する実現値) ・解像度∝1/IFOV 焦点距離:視野∝1/倍率 ・F値(口径比):焦点距離/口径 ・視野角(実視界):見掛視界/倍率 見掛視界:接眼lens単体の視界 ・倍率(焦点距離の比率):望遠鏡/接眼lens 感度:光の検出+記録能力(目視||camera||sensor) ・S/N比:Signal/Noise∝√(量子効率×露光時間) 量子効率:出力信号の電子数/入力信号の光子数(物理的な変換効率) ・ISO感度:出力信号のgain(noiseを含む増幅率) 天体観測 ・準備:主に天体追尾 水平出し:機材の安定化 極軸合わせ:自転軸の同期 ・撮影:S/N比の改善(hard/softの機能) 補償光学:seeingの改善 filter:光害cut||band-pass(色選択を含む) 天体追尾:ぶれの低減(自転を含む) 光芒対策(回折を除く):lens-hood ・光芒:光学現象 自然:薄明光線(大気中の散乱と遠近法) 構造:回折spike(点光源⇒sensor表面の不要な回折) ・反射望遠鏡:副鏡支持架 ・camera:絞り羽根 撮像:artifact(点光源⇒sensor表面の不要な反射||散乱) ・lens-flare:画面全体のcontrast低下(不要な散乱) ・lens-ghost:光源の虚像(不要な反射) digital処理:artifact ・A/D変換:量子化noise ・圧縮:block単位の平滑化noise ・後処理:画像処理 校正:noise除去 stacking:総露光時間=露光時間×stack枚数 ⇒ S/N比∝√露光時間 +位置合わせ:対象天体||背景天体基準(遥か彼方遠方) ⇒ 一方が筋状に流れる天体の追尾に相当 masking合成:対象天体+背景天体 強調:色||輪郭 抽出:構造pattern ・Larson-Sekanina filter:回転勾配の可視化(回転方向の差分画像) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
天体力学 の解釈 |
天体力学の解釈について記述する
定義 ・公転面:天体の公転面(公転の基準面) ・黄道面:地球の公転面 北黄極:黄道面の北極(上面図の視点) 軌道傾斜角:公転面と黄道面の交角 ・赤道面:天体の赤道面(自転の基準面) 赤道傾斜角:公転面基準 黄道傾斜角:黄道面基準 ・天頂角||極角:極軸に対する半角(円錐の広がりの半開き角度) ・立体角:幾何学的確率の基準 ・Hill球:主星に対する副星の重力圏の「Hill半径」 単純化:太陽-惑星-天体の円制限3体問題 ・Roche限界:潮汐力による破壊限界の「潮汐半径」 ・MOID(軌道間の最小交差距離≠実際の最接近距離):衝突riskの評価基準 天体の回転:公転と自転 ・太陽系:北黄極基準 順行:反時計回り 逆行:時計回り ・一般系:運動基準(公転方向と自転方向の符号 ⇒ rocket効果に対する変動分の影響) 「順行」:同一 ⇒ 進行方向の加速 「逆行」:反対 ⇒ 進行方向の減速 ・重力潮汐lock:自転と公転が同期する現象 潮汐力∝質量/距離**3:万有引力+遠心力の不均一分布に伴う相対的な力(例えば、地球-月の系) ・熱的潮汐lock:自転軸方向が太陽方向に同期する現象 斜めlock:熱的潮汐>重力潮汐(例えば、分厚い大気の金星) ・自転限界:重力=遠心力の状態の自転周期(一般的な彗星の場合、約4.7[h]) period_critical_rotation(rho)=<last{G=6.67430e-11,sqrt(3pi/(G*rho))}; period_critical_rotation(0.5e3)/(60*60) -> 4.668154259921848 効果:太陽光の吸収による加熱(作用) ・YORP効果:不均一な温度分布⇒異方性の熱放射(反作用)⇒回転速度||自転軸の変化(結果) ・Yarkovsky効果:不均一な温度分布⇒異方性の熱放射(反作用)⇒軌道の変化(結果) ・rocket効果:outgassing-jet(反作用)⇒軌道の変化(結果) ・Poynting-Robertson効果:放射圧(主な作用)⇒運動の減衰(反作用)⇒軌道の変化(結果) 抗力:入射角による光の収差+異方性のDoppler効果(特殊相対性理論の運動学的偏移) 摂動:天体軌道の乱れ ・惑星:主に重力(天体との相互作用) ・小惑星:重力||YORP効果||Yarkovsky効果 ・彗星:重力||rocket効果 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
軌道計算 の解釈 |
軌道計算の解釈について記述する
軌道計算 ・本来、地球の衛星である月の運動方程式を連成する ・また、別の天体の接近は地球の公転軌道||地軸に多少の摂動||章動を与える ・さらに、潮汐力で地球全体が変形するため、地殻||海面が追加の影響を受ける ・月の場合、潮汐力の影響が大きく、楕円体の長軸方向が地球方向に同期する(重力潮汐lock) ・より厳密には重力場と電磁場を含む系全体の相互作用によって摂動||章動が生じる ・例えば、太陽系が通過する宇宙空間のplasma等、大域的なenergy密度の変化が影響する ・よって正確な影響を予測する場合、太陽系内外で地球に接近する全天体の運動方程式を連成する ・一方、系全体の安定軌道を再現する初期値を確定困難のため、ある程度、独立して主要項のみ連成する ・また、滑らかな楕円軌道を想定して多項式近似の時間積分法(ODE高階行列関数)を適用する ・さらに、一般相対性理論の影響は数値誤差の範囲内と仮定する 実施例 ・swing-by:天体運動から得る加減速で軌道を変更する航法(力学的energy保存則 ⇔ 天体との弾性衝突) powered swing-by:重力assistに推力を併用 ・flyby:天体近くを通過すること(outgassing-jetを伴う彗星等) Ver.2.874.165以降、追記 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
天体 の解釈 |
天体の解釈を列挙する
・彗星 ・既知の天体 ・Tsuchinshan-ATLAS ・3I/ATLAS ・[引用]「人工物説」 ・仮説上の天体 ・反地球 ・Dyson球 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
彗星 の解釈 |
彗星の解釈について記述する
定義 ・E:天体の力学的energy ⇔ E:=Ep+Ek Ep:重力potential energy Ek:運動energy 恒星間天体(太陽系外から飛来の双曲線軌道 ⇔ E>0) ・1I/ʻOumuamua:観測史上初の小惑星?@2017/10/19(離脱過程で未解明の非重力的な加速現象を観測) ・2I/Borisov:2番目の彗星@2019/08/30(特有の非重力的な加速現象と近日点通過後に核の分裂を観測) ・3I/ATLAS:3番目の彗星?@2025/07/01(前例のない多くの特徴を観測) 太陽系天体(太陽の重力に拘束状態) ・惑星・準惑星・小惑星・衛星(楕円軌道 ⇔ E<0) ・彗星 周期彗星:軌道離心率<1(楕円軌道 ⇔ E<0) 非周期彗星:軌道離心率≧1(放物線||双曲線軌道 ⇔ E≥0) 長周期彗星:公転周期≧200年 ・紫金山・ATLAS彗星 短周期彗星:公転周期<200年 ・木星族:公転周期≦20年 ・Halley型:20年<公転周期<200年 太陽系小天体 ・小惑星:岩石と金属(主にFe-Ni合金)の凝集体 ・彗星:氷と岩石||塵の凝集体 大彗星:0等級を上回る明るさ(目視限界は約6等級で観測上の目安) 大彗星候補天体:太陽に「超接近」する軌道 ・"Sungrazer":近日点距離<3.45太陽半径 ・"Sunskirter":3.45太陽半径≦近日点距離≦33太陽半径 休眠(活動休止):表面に不活性な塵が堆積(一時的な表面の不活性化) 絶滅(活動停止):outgassingの活動性を消失(「燃え尽きた」小惑星遷移天体) 小惑星遷移:絶滅寸前の遷移状態 "Manx"(尾のない猫):低活動性で希薄な尾(小惑星に近い組成) ・"Rock from the Oort Cloud" 周回数終盤の長周期彗星(小惑星遷移 ⇒ 絶滅) ・"Lost":行方不明の天体(観測外の挙動を含む) ・流星物質:小惑星||彗星の断片(dust-trailの痕跡を含む) tail(尾の形態) ・dust-trail:断片の痕跡(outgassing-jetに伴う破片dust) anti-tail:見かけ上の「反尾」(軌道方向≒太陽方向に投影の接近より離脱過程で顕著) ・dust-tail:塵粒子の痕跡の「塵尾」(微細化を伴う) spiral-jet:核の自転による螺旋構造(自転軸方向≒太陽方向で顕著) striation:核の自転による扇状の縞模様(Synchrone線の粗密) ・plasma-tail:ionの痕跡の「主尾」(太陽からの紫外線と太陽風衝突で電離の昇華gas) ion:H2O+||H3O+||CO+||CO2+||HCO+||N2+ ray:筋状の構造 helix:螺旋状に捩れる||巻付く構造 kink:急激に折れ曲がる現象 knot:部分的な輝度の増減 DE:Disconnection Event 原理 ・活動の規模:活動度∝明るさ∝昇華率∝質量損失rate∝1/日心距離**光度係数 光度係数:4~6(活動度∝入射energyの理想的な場合、2) ・外向きのplasma-tail:一部ion化の電離gas ⇔ 超音速の太陽風plasmaの動圧と磁場(Lorentz力) 狭義の電磁相互作用:太陽風の動圧∝1/日心距離**2 ・内外向きのdust-tail:塵粒子(主に中性) ⇔ 太陽光の放射圧(光速の光子との運動量交換) 広義の電磁相互作用:太陽光の放射圧∝1/日心距離**2 ・粒径分布(個数基準のべき乗則):数密度∝1/粒径**(3+fractal次元≒0.7) ・Synchrone線(同時放出線):放出時刻の違い ・Syndyne曲線(等斥力線):物理特性β値の違い ・β値:β=放射圧による斥力/太陽の重力による引力∝1/(粒子密度*粒径) 高β値(β>0.1):sub~数μm 中β値(0.01≦β≦0.1):数~数十μm 低β値(β<0.01):数十μm~mm β≒0:cm~ 既知の影響 ・ion化の電離gas(plasma):太陽風で反太陽方向に分散して拡散(近日点>1auで到達なし) 到達の仮定:磁気圏との相互作用 ・中性gas:慣性維持で放射状に拡散(Haser-model) 到達の仮定:大気圏より極めて希薄 ・高β値の塵粒子:太陽光の放射圧で反太陽方向に分散して拡散(近日点>1auで到達なし) 到達の仮定:大気圏との相互作用 ・低β値のdust-trail:Order(1~10万年)で太陽に落下(Poynting-Robertson効果の螺旋軌道) 到達の仮定:dust-trail分布の粗密による衝突確率で流星群 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
既知の天体 の解釈 |
既知の天体の解釈について記述する
分類符号 ・C:非周期彗星(長周期彗星を含む) ・P:周期彗星 ・I:恒星間天体 ・X:不明確な軌道 ・D:消滅/分裂彗星
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
Tsuchinshan -ATLAS の解釈 |
Tsuchinshan-ATLASの解釈について記述する
Tsuchinshan-ATLAS:紫金山・ATLAS彗星 ・経緯:紫金山天文台で発見⇒追跡困難⇒ATLASで再発見(小惑星地球衝突最終警報system) 太陽系内彗星:彗星活動cycleの全processを網羅的に観測 観測網:以下の一覧(惑星探査機を含む)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
3I/ATLAS の解釈 |
3I/ATLASの解釈(西暦2025年基準)について記述する
10/21前後の天体show(非常に稀な事象) ・新月@太陽合:不可視(天体観測に最適) ・肉眼 Orion座流星群@極大期:東の低空@深夜⇒南東の高空@未明(主にMg自発発光の緑色) ・双眼鏡 Lemmon彗星@近地点:北西の低空@18~19時(二原子炭素C2の淡い緑色) SWAN彗星@近地点:南西の低空@18~19時(同上) ・望遠鏡 ATLAS彗星@近日点~近地点:南東の低空@未明 3I/ATLAS@太陽合:不可視(天体-太陽-月-地球が一直線に配列) 3I/ATLAS:3番目に発見@07/01の恒星間天体 ・以下、火星最接近@10/03以前の推定値と近日点~近地点通過後@2026/01/01以前の観測結果を参照 謎の信号:関連不明 ・発見の当日@07/01:"Wow! signal"の方向から飛来 ・発見の翌日@07/02:非常識なGRB 250702BDEの検出(3回反復) ・近地点の当日@12/19:不自然な25Hz狭帯域信号の検出(第4mode付近) 遭遇時期:第25太陽活動周期の極大期(予測より太陽活動が活発に推移@2525) ・黒点相対数の極大値(月平均換算)@第21⇒22⇒23⇒24⇒25途中:164⇒158⇒180⇒116⇒180↑ ・X-classの太陽flare発生回数@第21⇒22⇒23⇒24⇒25途中:90⇒95⇒130↑⇒50↓⇒50↑ ・異例:CME直撃event発生@09/24~25 Order(11年周期)に1度の頻度:地球の大規模なCME直撃event@2024/05/10~11@11/12~13 約5年に1度のExpo 2025 Osaka:The Farnese Atlas@Italy館@04/13~10/13 ・西暦2025年:戦後80年=令和7年(=平成36年=昭和100年=量子力学100年=量子仮説125年) 約14年に1度の超長時間gamma線burst:3回反復放出のGRB 250702BDE@07/02(飛来方向との離角≒17°) ・観測史上最遠のgamma線burst:単発のGRB 250314A@03/14(約131億年前の超新星爆発) 約15年に1度の「土星の環の消失」:環平面通過event@03/23@05/06@11/25 約1.2万年前に1度の頻度:Hayli-Gubbi火山の大規模噴火@Ethiopia@11/23 印象:高活動性で太陽系と真逆の啓示(特異な逆行軌道||物理的な逆尾||構造と組成の反転||逆因果律の示唆) 疑問:地球内外の主な探査probeの観測windowに痕跡を残す絶妙なtimelineと経路(必然のsynchronicity?) ・観測bias∝1/感度:明るさ||速度||時空間のwindow||幾何学的な経路に依存(発見自体が非常に稀な事象) CNEOS Fireball Catalog:飛来天体に占める恒星間天体の割合≒0.2%(Rubin天文台のLSSTで確認予定) ・前例:太陽系内彗星の紫金山・ATLAS彗星(2023/01/09発見~2年弱の期間の全processを網羅的に観測) ・異例:木星周回機Junoからの観測(来年の予定) ・超異例:木星探査機JUICEの補完的なrendezvous観測@太陽合@0.43au上流@11/04 ・超々異例:木星探査機Europa Clipperの補完的なrendezvous観測@太陽合@1.1au下流@11/06 通過点:最接近距離 ・太陽の近日点@10/29:2億292万km≒1.356au ・地球の近地点@12/19:2億6891万km≒1.8au 既知の影響:地球MOID≒5475万km≒0.366au>>coma半径+dust-tail長(直近の交差なし) dr=0.366; dr*149597870700 -> 54752820676.2[m](dr≒1.356-1) 直接観測の人工的な電波信号[GHz]:非検出@ATA@07/02@GBO@12/18(0.1[W]未満) 間接的な観測:非重力加速度による軌道vectorの経路変化と質量収支の整合性(撮像の時空間分布を含む) ・内容:質量損失割合下限の概算(model-basedの推定値) ・質量損失rate下限:180~405kg/s@2au~近日点(光度曲線から換算) 塵の散乱光(乱反射を含む):全波長領域(連続spectrum) ⇒ 中β値の塵粒子が主体 gasの蛍光発光:非常に狭い波長領域(輝線spectrum) ⇒ 希薄な影響(淡い着色) ・核の質量:48.5±2.2Tg@12/10(予測の33000Tgより3桁小さい) ・核の直径:約570m@12/10(予測の下限に近い) ・質量損失割合:分裂なし相当 m_rate=(180+405)/2; T_perihelion=18.5*60*60*24; dm=m_rate*T_perihelion; dm -> 467532000[kg] d=570.0649908033095; rho=0.5e3; vol=(4pi/3)*(d/2)**3; m=rho*vol; m -> 48499999999.99994[kg] dm/m -> 0.009639835051546404(分裂なし) a_non_g=2.5e-5; v_gas=300; a_non_g*T_perihelion/v_gas -> 0.1332(分裂あり) ・|非重力加速度|@近日点:Order(5e-7m/s^2) Marsden形式RTN3成分@11/27:動径:接線:法線方向の比率≒3:2:0(動径方向の外向き+「順行自転」相当) A1=7.67705176269127e-8; A2=5.097390576407114e-8; A3=-3.581097723791005e-9; sqrt(A1**2+A2**2+A3**2)*149597870700/(60*60*24)**2 -> 0.0000018481274287716393[m/s^2] ・OH分子の|熱拡散速度|:約800m/s(<局所的な|噴射速度|v_gas) a_non_g=5e-7; v_gas=1000; m*a_non_g/v_gas -> 24.249999999999968[kg/s](gas成分の質量損失rate) ans/405 -> 0.05987654320987647(magnitudeから換算の実効係数下限) ・jetの推力:vector和をscalar実効値に換算(単一の近似式を適用) 複数:推力vector=-Σ質量損失rate×噴射速度vector(より厳密には面積分) 単一:|推力|=全質量損失rate×平均|噴射速度|×実効係数(方向を含む) ・近日点付近:太陽側優勢のoutgassing-jetによる約4秒角の経路逸脱 deg_non_g=4/(60*60); deg_non_g -> 0.0011111111111111111[deg] ・近日点通過後:希薄な尾(太陽合の直後) ⇒ 徐々に幾何学的な視認性が回復(離脱過程) ・主要因:rocket効果>>>>>放射圧>動圧>Yarkovsky効果 d=570.0649908033095; rho=0.5e3; vol=(4pi/3)*(d/2)**3; m=rho*vol; A=pi*(d/2)**2; a_non_g=5e-7; F_rocket=m*a_non_g; F_rocket -> 24249.999999999967 P_wind=4e-8; F_wind=P_wind*A; F_wind*[1,50] -> (0.010209362254992568,0.5104681127496284) r=1.356; P_radiation=4.5e-6*(1/r)**2; F_radiation=P_radiation*A; F_radiation -> 0.6246428272936756 F_Yarkovsky=F_radiation*1e-3; F_Yarkovsky -> 0.0006246428272936756 検証結果:太陽系内彗星と対照的(≠常時真逆) ・analogy:構造と状況の既視感 構造:「汚れた雪だるま」の彗星 ⇔ porous電極活物質(表層の不活性化) 状況:正反のtail構造 ⇔ 「土星の環の消失」(輪⇒扇⇒edge-onの「二極化」) ・起源:超新星爆発の残骸で充満の分子雲@12/26(主にFeの少なさと低β値の塵粒子を説明) ・星間旅行:宇宙線曝露による核表層の不活性化 ⇔ Order(0.1~10m)のcrust形成 crust:不揮発性の古い有機物(Tholin)への変質層 ・重合反応:氷+活性な有機物→Tholin(tarのような暗い高分子炭素化合物) ⇒ 当初の赤色化 ・分解反応:H2O+宇宙線→H+OH ⇒ 表層:H2OよりCO2が豊富 ・再結合反応:CO+O→CO2 ⇒ 深層:CO2よりH2O+COが豊富(太陽系外縁部に同様?起源次第) crust厚さ:観測される彗星の活動度に影響 ・べき乗則の光度係数:3.8±0.3@10/21 ・初期のoutgassing:揮発性物質の減少(dust-mantle化) ⇒ 熱伝導性の低下(深層の熱保護+内圧上昇に寄与) ・近日点±18.5日:通常のH2O+COと豊富なCO2の爆発的な昇華 ⇒ outburst@10/29 ⇒ 収束@11/09 質量損失割合:0.96%×実効係数区間[0.06,0.06*7*3*2] ⇒ 核[表層,深層]の連続はく離(≠分裂)+破片dust d=570.0649908033095; vol=(4pi/3)*(d/2)**3; vol -> 96999999.99999988 r_crust=[2,10]; vol_crust=vol-(4pi/3)*(d/2-r_crust)**3; vol_crust -> (2027578.6654227376,9855368.647762075) vol_crust/vol -> (0.02090287283940969,0.10160173863672255) ・近日点を生還の要因:適度な距離||緩やかな自転||CO2昇華の冷却効果||核の芯の存在(重心を支える構造) 核の自転周期:16.16~16.79h>自転限界≒4.7h 荷電交換反応(e-捕獲⇒励起⇒基底状態):太陽風の高価数酸素のK殻遷移によるX線検出@XRISM@11/26 蛍光発光(hν吸収⇒励起⇒基底状態):光電離のCO+(青色)>光解離のCN(青色)>C2(緑色)>>NH2(赤色) ・CO2+hν→CO2++e-(光電離) CO2+hν→CO+O(光解離) ⇒ H2OよりCO2が豊富@JWST@08/06 CO2+hν→O+CO++e-(解離性光電離) CO2+hν→O2+C++e-(解離性光電離) ・CO+hν→CO++e-(光電離) ⇒ 太陽より青い@10/28(豊富なCO2由来?深層露出のCO由来?) ・H2O+hν→H+OH(光解離) ⇒ 恒星間天体の電波信号を初検出@10/24(H2O分光観測の補強) 周波数:1666±1MHz≒OH-radical吸収線+運動学的青方偏移(約15.6[km/s]で接近相当) H2O+hν→H2O++e-(光電離) H2O+hν→H+OH++e-(解離性光電離) ・COS+hν→CO+S(光解離) ⇒ 以降、太陽系内彗星同程度以下の寄与 ・HCN+hν→CN+H(光解離) ⇒ 枯渇気味のC2よりCNが豊富@08/19速報(comaの青色成分>緑色成分) 生命の前駆体(主な有機物):HCNよりCH3OHが圧倒的に豊富@ALMA@11/25(起源の補強) ・C2H2+hν→C2H+H ⇒ C2H+hν→C2+H(多段階の光解離) ⇒ 緑色成分の急増@10/31~11/04 緑色成分:色覚の感度peakの波長帯(青色成分より強調されやすい) ・NH3+hν→NH2+H(光解離) ・近日点通過後@11/05~09:希薄な尾 ⇒ 7本のjet構造 ⇒ 正反のtail構造(自転による幾何学的な変化?) 太陽-天体-観測者の位相角:10°前後(≒太陽合) ・地上の観測window:夜明け前の東の低空↑(逆行軌道の離脱過程) 等級∝log(1/明るさ):9~15等級@10/29~12/19(徐々に観測困難) +軌道傾斜角:175.11°(≒黄道面) +非重力加速度:法線方向のA3成分≒0(≒edge-on) ⇒View from Earth:反尾の顕在化(太陽側の軌道方向) ⇔ 主尾の潜在化(視線方向≒反太陽方向) ・黄道面通過event≒近日点@10/29:主尾と反尾の交角≒軌道傾斜角 ionのplasma-tail(主尾):反太陽方向の細長い一本線(青白い色) 塵のdust-tail(逆尾+反尾+塵尾+螺旋):太陽側の軌道方向から反太陽方向まで扇状に分散(青緑色) ・粒径分布@太陽側の軌道方向⇒反太陽方向:極大⇒極小 ⇔ 最低β値⇒最高β値 観測bias:中β値の塵粒子が主体 ⇒ 扇の両端部分は検出困難の可能性(stackingのnoise相当) coma(gasと塵の混合)の直径:10~18万km≒土星~木星(≠見掛size)>約8万km@HST@11/30 ・検出直径:塵(流体駆動)<OH(H2Oの光解離)<CN(HCNの光解離)<CO2(熱拡散) 塵:約8万km(可視光線観測@HST) OH:塵とCNの中間(紫外線観測@Swift+電波観測@SARAO) CN:約18万km(電波観測@ALMA+JCMT) CO2:~70万km超(赤外線観測@JWST+SPHEREx) 北黄極視点の公転と自転:時計回り(地球は反時計回り) ・収束判定条件:北黄極視点の上面図が「正反合」の扇状 ⇔ 地球視点の側面図が「正反」のedge-on 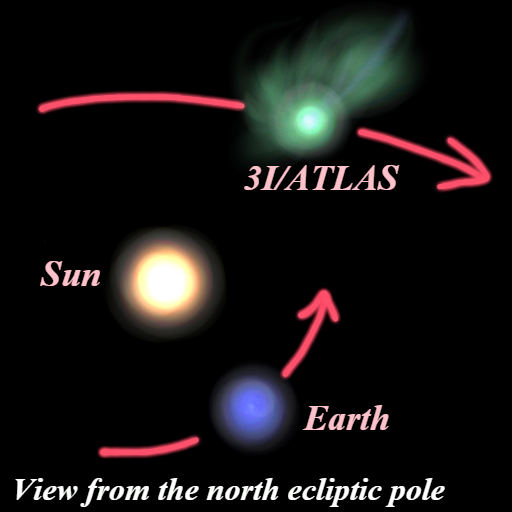 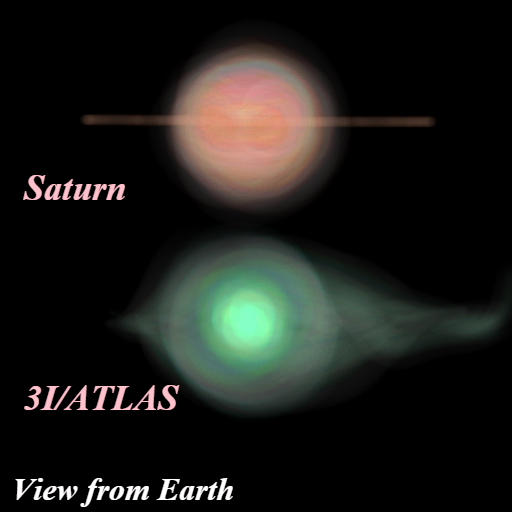
・outburstの収束@11/09:正反のtail構造 約95万kmのanti-tail(逆尾+反尾):太陽側の高圧jet+破片dustの累積的な分散(低β値の断片の滞留?技術的?) ・低β値の断片:軌道上に留まりやすい ⇒ 軌道方向に分布(≒太陽方向に投影 ⇒ 見かけ上の反尾) ・dust-trailの長さ:日心速力と正の相関 ⇒ 通常より長い(+高圧jetの影響) ・高β値の塵粒子:指向性のjet中心に追従しやすい ⇔ jet追従性∝β値(後述) 判別の提案@12/30:|逆流距離|>>0.5万km(技術的なthruster>>高活動性>通常の彗星) 構造の詳細@2026/01/01:核から2.4万km以内の不自然な3回回転対称性(Larson-Sekanina filter+stacking) 約285万kmのtail(通常の尾):放射圧で反太陽側に加速(主に高β値の塵粒子) ・高β値の塵粒子:反太陽側に流されやすい ⇒ 太陽の反対方向に分布 ・dust-tailの直線性∝1/曲率:日心速力と正の相関 ⇒ 通常より直線的 jet構造:活性spotの偏在化(強力な指向性) ⇒ 塵の微細化(衝突破砕)と高追従性(自転を含む螺旋) ・物理的な逆尾:活性spotとhot-spotの同期に由来の可能性(次の前例あり) 発見直後~近日点通過前:熱的潮汐lockに近い状態を継続(自転軸方向≒太陽方向) ・自転軸方向と太陽方向の交角≦8°:立体角の幾何学的確率≒0.5%(天頂角≦8°の球帽)(非常に稀な事象) (cos_deg(0)-cos_deg(8))/2 -> 0.004865965629214819 近日点通過後:夜側の活性spotが活発化+破片dustの残像(離脱過程の太陽側の軌道方向で顕著) ・McNaught長周期彗星:striation(核の自転と活性spotに由来) 縞模様の密部分:活性spotとhot-spotの同期区間(活性spotの法線方向≒太陽方向)の強力なoutgassing-jet 軌道傾斜角:77.5°(直交軌道の次同様に、「正反合」の扇状の構造を捉えやすい) ・Hale-Bopp長周期彗星:spiral-jet ・Halley短周期彗星:helix ・C/2011 L4 (PanSTARRS)長周期彗星:Order(100万km)のanti-tail(数週間で広範囲に分散の低β値の断片に由来) 核の日心速力:76.7~44.4km/s@近日点0.3~0.9au(近日点通過の約2月後の観測) ・311P/PanSTARRS小惑星帯彗星:6本のtail構造(高速自転による表面崩壊に由来) 核の直径:約0.4km 核の自転周期:5.4h以上(YORP効果で自転限界に到達) 放出event:高速自転による潮汐力と熱応力の相互作用 ⇒ 表面物質の間欠的な崩壊と放出(計9回) ・D/1993 F2 (Shoemaker-Levy 9)消滅彗星:21個以上の破片に分裂(木星の潮汐力のRoche限界突破に由来) Roche_limit(Rp,rhop,rhoc)=<Rp*(2.44*pow(rhop/rhoc,1/3)); Roche_limit(71492,1.33,0.5) -> 241698.79501289243[km](>最接近距離≒93600[km]) |脱出速度|:Hill球半径>>Roche限界 escape_velocity(r,mp)=<last{G=6.67430e-11,sqrt(2*G*mp/r)}; escape_velocity(241698.79501289243e3,1.8986e27) -> 32381.529281098563[m/s] escape_velocity(93600e3,1.8986e27) -> 52035.133553510015[m/s] ・C/2016 R2 (PanSTARRS)長周期彗星:H2OよりCOとN2が豊富(外縁部の最も始原的な環境に由来) ・3I/ATLAS:複数本のtail構造(自転を伴うoutgassing-jetに由来?技術的?) |非重力加速度|@近日点:Order(5e-7m/s^2) ・1I/ʻOumuamua:未解明の非重力的な加速現象(自転周期≒8.1[h]+不可視の水素氷説||solar-sail説) |非重力加速度|@1au:4.9e-6m/s^2>高活動性のOrder(1e-7m/s^2)>低活動性のOrder(1e-8m/s^2) ・上面位相角:10/21太陽合(負⇒正)/12/01(正)\2026/01/22(正⇒負)\2026/03/16木星最接近(負) 離脱過程の最中@12/15:活動度の減少傾向+主尾の潜在化傾向+約50万kmのanti-tail len=50e4; v=66; sec=len/v; sec/(60*60) -> 2.1043771043771042[h](≒総露光時間の移動距離相当に投影の残像) 観測網:以下の一覧(比較的短期間で深宇宙探査機の予定を含む) ・彗星の活動度∝昇華率:近日点付近で最大(特徴を捉えやすい) 望遠鏡画像:主に総露光時間がtail構造の濃淡に影響(加工次第) ・最接近時の光学的な最高解像度:Order(10km/pixel) ⇒ 核表面の解像困難 MRO (HiRISE):"3I/ATLAS looks like fuzzy white ball" with coma(短時間stacking@10/02の静止画像) ・追跡観測用のTGO (CaSSIS):粗いcomaの回転と移動(数日間@10/01~07の断続的な合成動画) ・追跡観測用のTianwen-1 (HiRIC):粗いcomaの移動(数時間@10/03の連続的な合成動画) ・不可視で不可解な矛盾の内包:multi-flyby@2525 重ね合わせ状態:偶然?必然?収斂?意図的?技術的? 反地球:次の影響なし(空想) 軌道計算:約4秒角の経路逸脱の補正前後で木星のHill球境界と交差が判明@11/22 ・木星最接近距離@2026/03/16:5344.5万km@11/22<Hill球代表半径≒5350万km<5377万km 補正量:-32.5万km ⇒ Order(10万km)でHill球の数値誤差の範囲内(swing-by効果の軌道修正?) 軌道投入要件:|相対速度|<|脱出速度| ⇒ |相対速度|≒66km/s>|脱出速度|≒2.2km/s(約30倍) escape_velocity(r,mp)=<last{G=6.67430e-11,sqrt(2*G*mp/r)}; escape_velocity(5344.5e7,1.8986e27) -> 2177.614788498567[m/s] escape_velocity(5377e7,1.8986e27) -> 2171.0237761395288[m/s] |相対速度|相当の重力捕獲距離:約5.8万km calc_r(ve,mp)=<last{G=6.67430e-11,2*G*mp/ve**2}; calc_r(66e3,1.8986e27) -> 58181019.191919185[m] ・Hill球:惑星の影響範囲 Hill_radius(a_mean,mp,ms)=<a_mean*pow(mp/(3ms),1/3); Hill_radius(778412010,1.8986e27,1.9884e30) -> 53147032.09345227[km](木星の公称値から単純換算) Hill_radius(149597870.7,5.9724e24,1.9884e30) -> 1496580.3474055005[km](地球の公称値から単純換算) Hill_radius(108208930,4.8673e24,1.9884e30) -> 1011154.3890076238[km](金星の公称値から単純換算) Hill_radius(227920000,6.4171e23,1.9884e30) -> 1083977.752539231[km](火星の公称値から単純換算) ・火星最接近距離@10/03:2897万km>>Hill球代表半径≒104万km(約28倍) ・反地球最接近距離@10/21太陽合:5500万km≒地球MOID≒5475万km(等倍) ・太陽最接近距離@10/29:2億292万km<<<<<Hill球代表半径≒2~30兆km(約1e-5倍) ・金星最接近距離@11/03:9716万km>>Hill球代表半径≒101万km(約96倍) ・地球最接近距離@12/19:2億6891万km>>Hill球代表半径≒150万km(約179倍) ・木星最接近距離@2026/03/16:5361万km@12/15≒Hill球代表半径≒5350万km(等倍)
起源:太陽系より始原的な環境(重金属が豊富な10~130[K]以下の極低温環境) 年齢:約70億年(例えば、超新星爆発のdustを含む原始惑星系円盤の外縁部に由来) 核の初期質量:約330億ton以上(非重力加速度が極小 ⇔ 高軌道安定性) d=5e3; rho=0.5e3; vol=(4pi/3)*(d/2)**3; m=rho*vol; m -> 32724923474893.676[kg] 核の直径∝√(観測の明るさ/反射率):0.32~5.6km(comaと分解困難 ⇒ model依存) 核の幾何学的albedo(反射率):0.04~0.10(当初の赤色化 ⇒ 経験則を適用) 核の自転周期:16.16~16.79h 核の自転方向:「順行自転」相当(進行方向の加速に寄与) 核の日心速力:58~68.3km/s(近日点で最大) ・初速要因:約220km/sで銀河中心を公転の太陽系に対する放出eventの相対速度(swing-byを含む) CO2のcoma直径(赤外線観測@JWST):~70万km超(近日点付近で最大) comaのgas成分:水より二酸化炭素、FeよりNiが豊富(核表層の多孔質構造||化学組成と揮発性に依存) 極端な負の偏光特性:核表層が高多孔質で弱結合の凝集体の可能性(comaの塵粒子の多重散乱を示唆) ・塵粒子の空隙率:空隙率に対する太陽光の偏光度が下凸の下限付近? 物理的な逆尾:太陽光の放射圧より太陽側のjetが優勢(水雪線より遠方での高活動性と低β値を示唆) ・comaの均一性:核表層からの揮発性物質の昇華(活性部分のoutgassing) ・outgassing-jetの非対称性:太陽放射の加熱で太陽側が活発(昼夜の温度差に起因) ・hot-spot移動の時間遅れ(1日程度):核の自転と熱慣性に依存(内部圧||地質||熱伝導を含む) 時系列の日心距離[au]:4.5(発見)⇒3.8(活発化)⇒3.2~2.7(水雪線) ・昇華物質:超揮発性物質(CO等)⇒+高揮発性物質(CO2等)⇒+水氷 CO:約25K@35au(海王星軌道以遠) CH4:約30K@20au(天王星軌道付近) CO2:約80K@5au(木星軌道付近) CH3OH:約100K@4au(小惑星帯外縁) H2O:約150K@3au(水雪線) Ni(CO)4:約43℃(carbonyl化合物の揮発性+光解離 ⇒ 分光観測でspectrum検出の可能性) Fe(CO)5:約103℃(核表面の最高温度相当 ⇒ 検出困難の可能性) Fe-Ni合金:1000℃以上(難揮発性 ⇒ dustのsample採取で検出) ・jet強度:極小⇒中⇒大 塵の微細化:弱結合のはく離(限定的)⇒せん断と衝突破砕⇒高速はく離と衝突破砕の激化 ・塵の粒径:大⇒中⇒小 β値∝1/粒径:小⇒中⇒大 jet追従性 ⇔ 「運動量交換の時定数」の逆数∝1/粒径:小⇒中⇒大(参考論文[4]) 質量慣性∝粒径**3:極大⇒大⇒極小 主体成分:古い有機物⇒未昇華の氷と有機物の混合⇒微細な無機物と有機物の破片dust(氷のgas化) ・可視光の特徴:赤色化(有機塵の反射光が優勢)⇒急激な増光⇒青緑色(gasの蛍光発光が優勢) ・尾の形態:微弱⇒物理的な逆尾(太陽側のjetが優勢)⇒通常の尾+見かけ上の反尾(太陽光の放射圧が優勢) ・今後:⇒2.64(Fe初検出)⇒2.4(火星最接近)⇒1.4(太陽合)⇒1.356(近日点)⇒1.8(近地点) 軌道計算:火星⇒反地球⇒金星⇒木星(「いて座」方向から逆行誘導で各1[au]以内のmulti-flyby) ・複数天体の整列(Hill球~1[au]の近傍通過):力学的な累積確率<0.005% ・軌道面と黄道面の極軸の交角≦5°:立体角の幾何学的確率≒0.19%(天頂角≦5°の球帽)(非常に稀な事象) (cos_deg(0)-cos_deg(5))/2 || (cos_deg(175)-cos_deg(180))/2 -> 0.0019026509541272274(黄道面に水平方向で順行||逆行の確率) (cos_deg(87.5)-cos_deg(92.5))/2 -> 0.04361938736533606(垂直方向の方が高確率 ⇔ 直交で極大化) 軌道傾斜角:175.11°(≒黄道面) ・放出event:黄道面と銀河面の交角≒60° ⇒ 薄い円盤より厚い円盤に近い可能性(起源の補強) ・不確定要素:星間の重力random-walk 太陽合(天体-太陽-地球):10月中旬~11月上旬(太陽光に隠れて地球から天体観測困難) ・特異性:黄道面通過event≒近日点@10/29 ・coronagraph観測:近日点に接近中の軌道と太陽の大規模なCMEを確認 幾何学的な補正要素:太陽の赤道傾斜角≒7.25°+地球の赤道傾斜角≒23.4°(静止軌道に影響) ・前後の期間:観測windowの短縮で観測困難(太陽-天体-観測者の位相角≒0 ⇒ 尾が視線方向の可能性) CME直撃event発生@09/24~25:太陽から突発放出の予測経路と交差(impact確率を下記) ・既知の影響:磁場反転⇒磁気再結合⇒plasma-tail切断event(例えば、2P/Encke彗星@2007/4/20) ・磁場∝1/日心距離:Encke彗星の約24%相当(主要因) (0.34/1.4) -> 0.24285714285714288 ・動圧∝1/日心距離**2:Encke彗星の約6%相当(希薄な影響) (0.34/1.4)**2 -> 0.05897959183673471 ・極大期のα=45°(天頂角≦45°の球帽)の立体角:Ω≒1.84[sr] alpha_deg=45; Omega=2pi(1-cos_deg(alpha_deg)); Omega -> 1.84030236902122 ・偏在の緯度範囲±40°(50°≦天頂角≦130°の帯状)の立体角 lat=40; Omega_AR=2pi(cos_deg(90-lat)-cos_deg(90+lat)); Omega_AR -> 8.077507329639102 ・活動領域と方向一致の確率:P_dir≒9.4% Omega_sphere=4pi; P_dir=(Omega/Omega_sphere)*(Omega_AR/Omega_sphere); P_dir -> 0.09413406600724783 ・軌道上で断面積の比率(中心円/盤面全体):P_geo≒0.00048% r_au=1.4; r2orbit=r_au*149597870700; P_geo(r)=<pi*r**2/(r2orbit**2*Omega); d_core=5e3; P_geo(d_core/2) -> 2.43239336115562e-16 d_coma=70e7; P_geo(d_coma/2) -> 0.0000047674909878650156 ・impact確率:P_dir×P_geo≒9.4%×0.00048%≒0.000045%(極めて稀な事象) 「人工物説」:「偶然の重なり」では説明困難の仮説(解釈の余地が残る) ・「生命体」||「自然物」||「漂流物」:multi-flyby(自己組織化||受動的な自己調整||擬態||意図的な誘導||偽装等) ・「無人機」||「有人船」:特異な太陽活動周期のmulti-flyby(帰還||探査||偵察||観察||補給||maintenance等) ・「ATLAS」:「天球⇒地球⇒世界を支える者⇒重荷を背負う者⇒耐え忍ぶ者」(太陽合で軌道修正?) 「宇宙の鏡」||「宇宙の意思」:CME直撃event(太陽と相互作用の挨拶||反応?) 「伝承の星」:赤⇒青緑の変色+稀有な同時天体show(大転換の示唆?) 「宇宙の物語」:以上を内包する"doramatic romance"(~超古代~1977~2025~年に渡る時空超越のanalog応答) ・「惑星の種」||「生命の種」||「Panspermia説」:宇宙規模の循環 「Fermi paradox」:「rare Earth仮説」||「暗黒森林理論」 ・「螺旋的循環」の弁証論:命題「正」と「反」の対立⇒真理の統「合」⇒torus表面の網羅 ・「Stokesの定理」のanalogy:±背反の渦⇒意識の止揚⇒渦構造の全体像(自己矛盾を動的に内包) 2025年:約1.2万年前?@起源不明の『Bugaの球体』の発見(seamless幾何表現の具現化?) 1977年:Star Wars⇒"Wow! signal"@8/15⇔Voyager 2号@8/20⇒1号打上げ⇒『未知との遭遇』(黄金盤+映画公開) Voyagerのゴールデンレコード(黄金盤):55の言語の挨拶「こんにちは、お元気ですか?」等を収録のanalog音盤 "Wow! signal":観測window≒72秒間の単発で強力な水素線周波数≒1420.4MHzの電波信号 ・周波数:1420.4556±0.005MHz=水素線周波数+運動学的青方偏移(約10.5[km/s]で接近相当) eta=1420.4556/1420.40575; ee=eta*eta; c=299792458; v=c*(1-ee)/(1+ee); v -> -10521.21324172012[m/s] ・「6EQUJ5」:「いて座」方向の固定点源らしき信号強度S/N比(背景noise標準偏差×36進数)の凸型波形の記録 ・「いて座」方向の一致:立体角の幾何学的確率≒0.6%(天頂角≦9°の球帽)(非常に稀な事象) alpha_deg=9; Omega=2pi(1-cos_deg(alpha_deg)); Omega_sphere=4pi; Omega/Omega_sphere -> 0.006155829702431115 r=58e3*60*60*24*365.2422*12*4; r/149597870700 -> 587.2709403926029[au](≒0.01[光年]のsignal発信源?) Snu=250e-26; dnu=[1,10e3]; F=Snu*dnu; A=4*pi*r^2; Ptx=F*A; Ptx -> (242481.00291029946,2424810029.1029944)[W](帯域幅dnu次第でkW~GW級の送信機出力×gain相当) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
[引用] 「人工物説」 |
「人工物説」についての引用
・1~3:対話部分 ・4~5:Gemini 2.5による追加の主張
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
仮説上の天体 の解釈 |
仮説上の天体の解釈について記述する
仮説上の天体 ・直接観測不可の場合、間接的な観測結果と軌道計算の整合性次第 ・惑星X:外縁天体の観測結果と軌道計算の矛盾を解消するための仮定(未知の惑星) ・惑星Nibiru:fiction上の過酷な惑星質量天体(長楕円軌道で傾斜角が大きく、約3600年周期で「交差」) ・ploonet:衛星が惑星軌道を脱出して長楕円軌道の惑星に移行(観測困難で未発見) ・反地球:地球のみ空想される不自然な天体 ・Dyson球:恒星を覆う人工的な球殻(赤外線天体として観測を想定) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
反地球 の解釈 |
反地球の解釈について記述する
対||反地球 ・対地球:太陽に対して点対称の位置を公転(公転面と焦点を共有する対称な楕円軌道を周回) ・反地球:太陽に対して反対側のLagrange点L3を公転(同一の楕円軌道を周回) ・対||反地球質量≒地球質量(公転周期が一致) ・摂動を含めて太陽の陰に隠れる大きさ(地上から常時観測不可) ・なお、entropy増大則に反するため、自然形成は想定しない(両天秤が釣り合う絶妙な秩序balance) Hopi族伝承 ・青い星:反地球を隠喩(終わりの始まりを告げる存在⇒天空で踊るrendezvous相手) ・預言:balance崩壊⇒反地球が出現⇒徐々に接近⇒天空に青い星が出現(浄化の日)⇒急接近⇒rendezvous |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
Dyson球 の解釈 |
Dyson球の解釈について記述する
Dyson球 ・恒星の放射を遮るような人工物の場合、放射量が間接的に低下(赤外線に変換)するため、系全体に影響を及ぼす ・地球の場合、太陽から到達の放射強度が3%低下(太陽定数*0.97を仮定)で地表の平均気温が約2℃低下する ・元来提唱の人工生物圏は以上の影響が少ないenergy利用が想定される ・当面、系全体(主に惑星)に配慮が必要な場合、Kardashev scaleの一部は制限される ・以上より、広義のhabitable zone(最大限の配慮)を含む恒星系は除外する可能性が高い ・一方、本来の生物圏は不安定な表層より深層に安定性を見出す可能性がある |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
気候変動 の解釈 |
気候変動の解釈について記述する
気候変動 ・系内部の発熱量と放熱量の熱平衡状態から偏りが発生すれば温度が変化すると言えるが、 ・偏り発生の要因と寄与度の因果関係が本質的に問題となる ・自然の長期変動に対して温暖化が急速に進行中のため、人為的な温室効果gasの排出が主要因とされる ・とくに、大気中の二酸化炭素濃度の増加と温暖化には強い相関が見られる(大気の吸収率増加) ・そのため、森林減少の影響も大きい(「総排出量の内訳」参照) ・また、簡単には追従しないであろう、副次的な環境変化への影響を考慮する ・例えば、気温上昇(放射強制力増加)が停止しても、雪氷由来のalbedo低下と海面上昇は即座に停止しない ・一方、北半球は南半球より顕著な影響が見られる(人口と陸地面積率の数倍差を含む) ・このような場所による偏りの拡大は気象現象を異常||激甚||極端化する可能性がある(熱赤道付近の台風等) ・他方、温室効果以外の直接的な要因として、太陽と地球の相対的な運動||活動による寄与度が大きい ・現状、太陽放射の強度は太陽活動周期に渡ってほとんど変化しない(変動量<0.1%)が、 ・今後、それら運動||活動の影響(小氷期到来||albedo増加)で(一時的に)寒冷化が優勢になる見方も存在する ・その他、地磁気の弱化||pole shiftと未知の天体接近による可能性が指摘されている その他の議題:自然の大循環||環境汚染||環境破壊||気候災害||自然災害||食糧問題||大量絶滅 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
主要因子 の解釈 |
気候変動の主要因子の解釈について記述する
主要因子 ・太陽定数[W/m^2]:放射線に対して垂直な面の太陽放射の強度 球対称の放射:強度∝1/日心距離**2 ・大気の吸収率:全球の放射線を吸収する効率(大気中の温室効果gas濃度に依存) 温室効果gas:地表からの赤外線を吸収 ・albedo:全球の放射線を反射する効率(主に氷床の残存量と雲の総量に依存) 真白の地域:地表で最高の反射率(9割) aerosol:吸収<反射の寄与 ・雲の総量と高度:4通りtotalの寄与度変化小||未知数(主に下層雲の減少と上層雲の高度上昇を懸念) 下層雲||日中:吸収<反射の寄与 ⇔ 温暖化と負の相関 上層雲||夜間:吸収>反射の寄与 ⇔ 温暖化と正の相関 ・放射強制力[W/m^2]:対流圏界面の熱流束fluxの変化量(熱量収支の統一指標) 系全体の平均気温の変化:統一指標換算で要因の寄与度を議論 ・日射[W/m^2]:地表換算の放射強度(Milankovitch仮説の地球の運動周期に依存) 地表spotの平均気温:日射の地表分布のspot依存 単純平均:I0=1367; I0/4 -> 341.75 albedo加味の最大値:I0=1367; I0*(1-0.3) -> 956.9 夏至の正午@北緯30[deg]:I0=1367; I0*(1-0.3)*cos_deg(30-23.4) -> 950.5583994030193 冬至の正午@北緯30[deg]:I0=1367; I0*(1-0.3)*cos_deg(30+23.4) -> 570.5275828545979 ・|緯度|[deg]:spotの日射量に直接影響(主に北半球の大陸氷床) 極圏の境界区間:90-[24.5,21.5]=[65.5,68.5](地軸の傾き減で極圏の日射減) 陸地面積率最大(約7割)の区間:北緯[60,70) ・陸地面積率:=陸地/(陸地+海洋):全体に対する陸地の面積割合(自然の大循環に影響) 北_陸:北_海:南_陸:南_海≒20:30:10:40[%] 熱容量:土壌<海水(海洋の蓄熱効果と熱輸送の時間遅れ大) ・自然の大循環:熱と物質を輸送する自然界の循環(主に大気と海洋||森林の循環) ・応答の時間遅れ:入力に対して応答が遅れる時間の目安 ・熱輸送の時定数:気温変化に伴う1次遅れ系の時間遅れ(主に大陸氷床と海水準に影響) 1次感度(対流圏内の放射⇒対流):Order(0.1~1年) 1.5次感度(大気⇒海洋表層~深層の伝達⇒対流):Order(0.1~10年) 2次感度(大気と海洋⇒対流圏外の伝達⇒拡散):Order(100~年) ・地盤変動の時定数:荷重変化に伴う1次遅れ系の時間遅れ(風化の痕跡||標高依存の質量収支に影響) 海水||氷床の荷重:Order(1千~1万年) 補足因子 ・地球の熱源(地熱energy):地表換算のflux=42e12/510100000e6=0.08233679670652813[W/m^2] 地殻とmantleの放射性崩壊:8+12=20[TW] 液体金属核冷却の仕事率:42-20=22[TW] |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
従属関係 の解釈 |
主要因子の従属関係の解釈について記述する
従属関係(顕現順) ・変動 気温(起点を仮定) ⇒海水温 ⇒albedo(主に氷床と雲) ⇒海水準と温室効果gas(主に二酸化炭素とmethane) 自然界の「正のfeedback-loop」 ・氷期⇒間氷期 温暖化(負のloopより顕著の前提) ⇒海水温上昇 ⇒雪氷由来のalbedo低下(日射と温度のpeak時間差の一因) ⇒海面上昇と大気中の温室効果gas濃度増加(大気と海洋の循環作用) ・停止機構:北極の日射peak以降、徐々に温度peakで大陸氷床の後退から成長に逆転(南極の時間遅れが最大) ・非対称性:氷床の後退:成長時間[万年]≒1:9(逆のこぎり波の波形) 後退の温度上昇rate:日射と氷床の変動に従属(熱暴走なし) ・間氷期⇒氷期 寒冷化 ⇒海水温低下 ⇒雪氷由来のalbedo増加 ⇒海面下降と大気中の温室効果gas濃度低下 気温変動の駆動力 ・自然:太陽の日射>>地球の熱源 ・外乱:「人為起源温室効果ガス総排出量の内訳」(温暖化の「正のfeedback-loop」に介入) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
変動rate の解釈 |
変動rateの解釈について記述する
変動rate ・気候変動の基準年 開始年:西暦1900年(balance状態) 基準年:西暦2000年(温暖化が優勢 ⇒ 海水回帰の融解rate>>湿度依存の降雪rate) ・平均気温の上昇量[℃]の区間(想定) 最終氷期⇒間氷期:[7,10] 西暦2000年:1(海水温同様に、100年で上の10~14%の進行度) ・平均気温の上昇rate[℃/年](目安) 最終氷期⇒間氷期:[7,10]/(1.8e4-0.6e4)=(0.0005833333333333334,0.0008333333333333334) 西暦2000年:1/100=0.01(自然界の「正のfeedback-loop」に従属の上に対してstep入力相当) ・全海洋平均の海面上昇量[m](目安) 最終氷期⇒間氷期:120 西暦2000年:0.2 ・平均気温の上昇量に対する海面上昇量[m/℃](目安) 最終氷期⇒間氷期:120/[10,7]=[12,17.142857142857142] 西暦2000年:0.2/1=0.2(step応答で上と2桁差 ⇒ 長時定数の蓄積で顕現) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
海面上昇 の解釈 |
海面上昇の解釈(西暦2000年基準)について記述する
温暖化に伴う全海洋平均の海面上昇 ・海水準の変動rate[mm/年](目安) 最終氷期⇒間氷期:120e3/(1.8e4-0.6e4)=10 約1.4万年前のmeltwater pulse:40(北半球大陸に南下成長の氷床の崩壊) 西暦1900年前後:0.1~0.2 ⇒ 1~3 西暦2000年:1.6+1.19=2.79 ・西暦2000年のrate内訳(目安) 海水の熱膨張:1.6 雪氷の融解:0.77+0.21+0.21=1.19 氷河と氷帽:0.77 Greenlandの氷床:0.21 南極の氷床:0.21 その他:3.1-(1.6+1.19)=0.31 地下水汲み上げ:高度成長期の一因 ・海水準換算の残存量[m](目安) 氷河と氷帽:0.5 Greenlandの氷床:7 南極の氷床:60 北極の海氷:浮遊(海水準より極渦のjet気流に影響大) ・海水温の上昇量[℃](目安) 最終氷期⇒間氷期:2.3 西暦2000年:0.3 ・気温変化に対する追従性 海水の熱膨張:多少の時間遅れで追従(当初の変動rateの大半) 雪氷の融解:複数spotで熱伝達⇒熱拡散を伴うOrder(100年)の時定数で顕在化(徐々にrate増の可能性) ・時定数の根拠 9000~6000年前:日射peak以降の海面上昇の緩和過程に適合(温度peakの時間遅れを含む) 約7700年前:平均気温の温度peakの推定時刻 西暦1900年~:緩和過程の延長で流用(長期のbalance状態を想定) ・長時定数の影響 温暖化:「正のfeedback-loop」 突発のmeltwater pulse@rate>0:Order(10年)の大洪水event(当時よりspot減の残存量次第) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
温室効果gas の解釈 |
温室効果gasの解釈について記述する
温室効果gas ・温室効果gasは大気の吸収率に関係する ・以降、大気中の温室効果の促進を想定する 温室効果gas濃度が増加(駆動力を仮定) ⇒大気の吸収率が増加(正の相関) ⇒太陽から流入する放射と地表から流出する放射の吸収量が増加(主に後者の赤外線を吸収⇒再放出) ⇒宇宙に透過する放射量が低下 ⇔ 地表への到達量が増加(正の放射強制力) ⇒平均気温が上昇(温暖化) ⇒温度変化量=放射強制力の電力量/熱容量 ・温室効果なしの黒体放射温度≒-18[℃] 地球温暖化係数[GWP]:単位重量当たりの温室効果能力(残留期間に依存の目安) ・二酸化炭素:1 ・methane:Order(10) ・一酸化二窒素:Order(100) ・F-gas:Order(1000~10000) 残留期間:大気中に排出~化学反応で分解の期間(目安) ・二酸化炭素:非常に安定(自然の大循環次第) ・methane:約12年(対流圏のOH-radical反応) ・一酸化二窒素:約110年(成層圏の紫外線で光化学反応) ・F-gas:Order(10~1000年) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
二酸化炭素 の解釈 |
二酸化炭素の解釈(西暦2020年基準)について記述する
大気中の二酸化炭素濃度 ・前提:温室効果gasの主要因子で信頼性の高い古気候dataを蓄積済み ・億年scaleの傾向:濃度は減少傾向 ⇔ 太陽放射の強度は増加傾向(今後、全球凍結は起こり得ない) ・自然cycle(Milankovitch cycle)の濃度変動[ppm]:190~280(albedo=[0.36,0.39]~0.3相当の氷床の変動に従属) ・直近の濃度変化[ppm]:280~410(万年scaleの間氷期の上限を超えて高rate≒2[ppm/年]で増加中) 平均的な傾向:大気>海洋の分圧(大気側の超過) ⇒ 海洋の吸収量>排出量(海水温に依存) ・予想の目安 直近の気温変化との相関:100ppmの濃度変化量 ⇔ 約1℃の気温変化量 一意の相関の仮定:濃度小の線形領域 大気換算(全因子を含む)の経験則の仮定:大気の吸収率係数=1-0.013*(280-ppm)/(280-190) 代表濃度ppmの実質寄与度の想定:熱容量加味の気候感度から半分~大半(「総排出量の内訳」参照) 全球凍結なしの根拠(極端なalbedo増加を除く):-280ppm ⇔ 約-3℃(温室効果gasの全回収相当) 氷期の平均気温の変化量:-[7,10]℃=-1℃(大気の吸収率低下)-[6,9]℃(albedo増加) 超過の深刻度:超過量/自然変動の振幅=(410-280)/((280-190)/2)=2.888888888888889(rate未考慮) ・当面の予想:「超」間氷期で温暖化が優勢(次の氷期は北半球の大陸氷床が成長に反転するか次第) 大方の懸念:自然cycle逸脱で定量予測困難(海洋の吸収限界||暴走modeの閾値||氷床の最終残存量等) 副次的な影響:気温変化に従属の熱伝達⇒熱拡散の影響はOrder(100年)の時定数で顕在化(海面上昇等) 逆説の補足:濃度超過が従属の場合、実際の気温変化量に対してrate過大||過敏 ⇒ 濃度超過が駆動力 極論の比喩:地球環境の金星化が闇雲に加速(実験室level) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
[引用] 総排出量 |
「人為起源温室効果ガス総排出量の内訳(2004年・二酸化炭素換算)」
・二酸化炭素:56.6+17.3+2.8=76.7% 化石燃料利用:56.6% 森林減少:17.3% その他:2.8% ・methane:14.3% ・一酸化二窒素:7.9% ・F-gas:1.1% 以上、抜粋して引用:環境省の資料900422877.pdf「森林の減少と温暖化」の円graph ・Ver.2.619.97以降、分子名の誤植を訂正 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
空気力学 の解釈 |
空気力学の解釈について記述する
空力特性 ・3軸 x:正面の推進方向 y:推進方向と垂直な左右方向 z:推進方向と垂直な上下方向 ・3軸の力成分 x:抗力 y:横力 z:揚力 ・3軸の回転軸 x:roll y:pitch z:yaw 実施例 ・自動車||robotics:左手系 ・飛行機:右手系 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
野球 の解釈 |
野球pitchingの解釈について記述する
・Ver.2.515.90以降、spinから解釈として移植(軸定義の補足を更新) 左手系の回転軸の定義(空力特性と未統一) ・進行方向のx'軸:jyro-spin(jyro) ・+y'軸:side-spin(screw) -y'軸:side-spin(slider||sweeper) ・+z軸:back-spin(fork||straight) -z軸:top-spin("縦の"slider) ・billiard||tennisと異なり、top-spinの投球は難しい Magnus効果 ・Magnus力=流体密度×進行速度×循環 循環∝回転の角速度 ・力の向きは進行方向と回転軸の両方に垂直(旋回の向心力同様に、仕事なし) ・Magnus力の比例係数:Cl 重力の影響 ・y方向落下速さ(落差の微分値)からx方向のMagnus効果が生じる ・back-spinの場合、top-spinより若干、x方向の進行が速い ・また、落差が小さく、若干、運動energyが小さい(力学的energy保存則) ・空気中の場合、密度比から生じる浮力の影響は小さい(空気/球の密度比<<1) ・Coriolis力の影響は数値誤差の範囲内で考慮しない jyro-spinの影響 ・y'-z面変化量の微分値からz軸成分のMagnus効果より一桁小さい ・spinの回転方向に応じて無回転より若干、y方向に上下する ・screw効果で後流のはく離が小さく、安定的に空気抵抗を低減する ・よって、失速の程度が小さく、球速が伸びる ・Ver.2.425.89以降、乱流を想定して抗力と速度の関係を修正(軌道変化を明確化) 層流の抗力∝速度(Stokesの抵抗則) ⇒ 乱流の抗力∝速度**2(Newtonの抵抗則) ・抗力の比例係数:Cd 無回転 ・後流の渦放出が不規則で軌道が安定しにくい ・境界層を含む表面粗さの影響を受けやすい 球の規則的な振動(目安) ・St=0.2を仮定 ・到達時間[sec]=18.44/40=0.461 ・渦放出の振動周期[sec]=(73e-3/40)/0.2=0.009124999999999998 ・渦放出の振動回数=0.461/0.009124999999999998=50.52054794520549 循環の空間積分 ・簡単化する場合、比例係数×回転数で代替 ・非厳密のため、回転数のみに依存する1次の回転減衰効果を仮定(粘性の摩擦抗力が主要因) Ver.2.425.89以降、流体密度を含む有次元の比例係数を無次元化 ・回転減衰の比例係数:Cf |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
飛行機 の解釈 |
飛行機の解釈について記述する
飛行機の翼 ・揚力:推進中に翼の下面(正圧)と上面(負圧)の圧力差で生じる上向きの力 Bernoulliの定理:翼の上下で流速が異なるため、全圧から上下の圧力差に換算 循環:物体周りの閉曲線に渡る速度の線積分(流れ場が上下対称の場合、循環=0) Magnus効果:翼は回転していないが、循環≠0のため、Magnus効果の力≒揚力 揚力の厳密な計算:圧力の面積分(表面の法線vectorを考慮) ・摩擦抗力成分の厳密な計算:摩擦応力の面積分(表面の接線vectorを考慮) 壁法則:境界層の速度分布と壁面摩擦応力の関係を表す法則 ・翼型(断面形状):上面の流れがはく離なしで合流する最適形状の流線型(はく離で失速) 対称翼(上下):よどみ点を下側に制御することで揚力が発生(仰角>0) 縦渦発生装置:前縁に設置して後流のはく離を抑制 ・旋回:旋回の中心方向の翼を下げて揚力の水平分力を向心力に変換 水中:浮力支配の場合、下向きに潜る力の水平分力を向心力に変換 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
jet の解釈 |
jetの解釈について記述する
jet ・宇宙jet:重力天体の単極||双極の軸方向に噴出するplasma等のjet(線のように映る) ・jet気流(偏西風):対流圏上層にあり、飛行機||台風の進路に影響(軽い程、蛇行して流されやすい) ・jet雲:jet飛行機engine後流に発生(高温の排気gasが凝縮) ・筒内直接噴射式内燃機関:液滴群との運動量交換でgas噴流のjetを形成(噴射圧力||RPM等に依存) Bernoulliの定理:|噴射速度|∝√(噴射圧力-雰囲気圧力) 実施例 ・jet気流を可視化する場合、Bénard6cells参照(Coriolis力で形成の渦列を平面に投影) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
大気圏 の解釈 |
大気圏の解釈について記述する
各高度範囲(概要) ・大気圏:0~100km ・宇宙空間:100km~ ・対流圏:0~8(極)~17(赤道)km ・成層圏:8(極)~17(赤道)~50km ・中間圏:50~80km ・熱圏:80~800km ・外気圏:800~10000km ・電離層:60~800km ・ozone層:10~50km ・磁気圏:1000~60000(太陽側)~1000000(反太陽側)km ・plasma圏:800~20000km ・均質圏:80~90km ・乱流圏:100~110km ・拡散圏:110km~ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
地球史 の解釈 |
地球史の解釈(西暦2000年基準)について記述する
地球史 ・約23億年前の全球凍結:史上最初の全球凍結(太陽放射の強度=現在基準値×0.8275) ・約7億年前の全球凍結:史上最後の全球凍結(太陽放射の強度=現在基準値×0.9475) x十億年前の1次関数を仮定:太陽放射の強度係数=1-0.33*x/4.4 現在基準値との比較:二酸化炭素濃度とalbedoが非常に高い ・約6600万年前の隕石衝突:Yucatan半島に小惑星が衝突⇒粉塵を生成⇒地球規模の寒冷化⇒大量絶滅(恐竜を含む) 粉塵で反射率が3割増を仮定(albedo=0.3⇒0.39):平均気温が約9℃低下 自転軸への影響:size比依存で小さい(地球直径に対するsize比≒0.001) ・約300万年前:北半球に大陸氷床が出現 ・約258.8万年前の更新世~:氷期+間氷期cycleの開始 ・約77万年前の地磁気逆転:直近の反転 ・約40万年前の現生人類の出現期~:Milankovitch cycleが主導(約10万年の周期) 大気中の二酸化炭素濃度の推移:化石燃料を大量消費する文明の痕跡なし 次のToba事変:濃度変化は自然変動の範囲内(気温変化を含む火山活動の影響に対して感度小の可能性) ・7~7.5万年前のToba事変:火山の超巨大噴火⇒火山灰を生成⇒地球規模の寒冷化(約6000年間継続) 火山灰で反射率が2割増を仮定(albedo=0.3⇒0.36):平均気温が約6℃低下 急激な寒冷化の痕跡(氷床coreの酸素同位体比):Greenlandはあるが、南極はない ・1.8~0.6万年前の最終氷期⇒間氷期:温暖化⇒海面上昇120m⇒陸地減少 海水回帰の過程:氷床の後退+大陸上に蓄積の雪氷の融解(氷期の陸地侵食⇒風化の痕跡あり) ・1.29~1.15万年前のYounger Dryas期(欧州一帯):温暖化⇒急速に寒冷化(逆戻り)⇒農耕の開始 逆戻りの原因:熱塩循環の弱化||彗星衝突の可能性 ・~6000年前の縄文海進:海面上昇による地盤変動を含む縄文時代前期の海進(場所によって進度の痕跡差あり) ・約4500年前の古代Egypt:Gizaの3大pyramidを建造 「重量拡散の間」最上層の壁面に残る複数のhieroglyph:「khufu」の「17回目の牛を数える年」 同上のcartouche(王名枠):「raa(h)ta」説あり(約1.2万年前の獅子座の時代) 大Sphinx前足発掘の碑文の最後:「khaf」(Khafra王の時代が定説) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
完新世 の解釈 |
完新世の解釈(西暦2000年基準)について記述する
第四紀氷河時代 ・更新世:258.8~1.17万年前の氷期+間氷期cycle ・完新世:約1.17万年前の最終氷期⇒間氷期の現在 最終氷期:日本列島と大陸が地続きの時代(一時的) 間氷期:温暖な気候で農耕||牧畜の開始 ・時系列の平均気温||海水準と静水圧||陸地面積率||大気圧||二酸化炭素濃度||酸素濃度||骨格等の推移次第 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
海水準 の解釈 |
海水準の解釈(西暦2000年基準)について記述する
海水準 ・海水準:陸地に対する海面の相対的な高さ(地殻変動に依存) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
起源 の解釈 |
起源の解釈(西暦2000年基準)について記述する
地球の起源 ・宇宙創成:約138億年前(big-bang仮説) ・銀河誕生:約130~132億年前 ・地球誕生:約46億年前(giant-impact仮説) 人類の起源 ・Gorillaと分岐:約1000万年前 ・Panと分岐:500~800万年前 ・現生人類誕生:25~40万年前 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
DNA の解釈 |
DNAの解釈について記述する
現生人類のDNA ・DNA:約30億塩基対(目安の基準値N) ・塩基配列 個人差:0.1%程度(Toba事変で縮小) Panとの差異:1.6%程度 Gorillaとの差異:2.3%程度 ・突然変異の長期平均rate[塩基対/年]:4.5±1.5(近縁種を含めて重複なしの均等配分p=0.5を仮定) calc_rate(ts,te,percent,p)=<[N=30e8,t=(te,ts),r=(percent/100)*p,rate=N*(r/t),=<rate]=>; calc_rate(25e4,40e4,0.1,0.5) -> (3.75,6) calc_rate(50e5,80e5,1.6,0.5) -> (3,4.8) calc_rate(100e5,100e5,2.3,0.5) -> (3.4499999999999997,3.4499999999999997) ・細胞周期:G1(checkpoint)⇒S⇒G2(checkpoint)⇒M期 M期:細胞分裂 細胞分裂の回数上限:50回 年平均の細胞分裂回数[回/年]:M S期:DNA複製 突然変異の発生確率P:1e-9(長期平均rate換算) calc_P(rate,M)=<[N=30e8,P=rate/(N*M),=<P]=>; calc_P(3,1) -> 1e-9 calc_P(4.5,1) -> 1.5e-9 calc_P(6,1) -> 2e-9 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
数の概念 の解釈 |
数の概念の解釈について記述する
数の概念(自然発生順を想定) ・個数・自然数 ・整数(0±自然数) ・数字・進数・桁数 ・素数・合成数 ・公約数・公倍数 ・有理数・無理数 ・円周率・代数 ・分数・小数 ・対数 ・実数・度数法・弧度法・複素数・四元数・vector・行列 ・示量性状態量(体積||entropy) ・示強性状態量(温度||速さ||濃度||電位potential) ・quality・実数ε 定義の補足 ・円周率の基準径:実用性の直径||面積のanalogyの半径(幾何学の時代背景に依存) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
pyramid の解釈 |
pyramidの解釈について記述する
当時の建設目的の解釈を記録 ・主流 王の墓||祭壇||叡智の神殿(複数の位置関係で星座を表現) 天体観測(春分の日等、光と影の演出あり) ・一部 公共事業説 貯蔵庫||蓄電装置||発電所説(電離層||水||雷||太陽光prism||plasma等を利用) 活性化||通信||交信(天地の兆候を含む)||輸送||転送装置説 着陸の目印 物質優位で精神的隷属の輪廻||trap装置 ・建築手段 加工:切り出し 運搬:水路||陸路||内外坂路(浮力||ころ||てこの原理を応用) 不明:巨人族||先進文明の関与 海底に沈む水晶pyramid(詳細不明) ・直近の地磁気を誘導(圧電率||吸水率||誘電率を材質で調整) ・地||水||音等の振動を本体で増幅して磁束回転場に変換 ・本体の一部||球体のcapacitorに電荷を蓄電 ・余剰な電荷を電場に沿って頂上から上空||地下に放出 ・地震の前兆を検知(地磁気の異常||過剰な電荷を検知) ・以上より、不安定な影響を考察 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
geometry の解釈 |
geometryの解釈について記述する
pyramidのgeometry ・底辺長:L=230.3; 底辺長半分値:Lh=L/2; Lh -> 115.15 対角線半分値:Lh*sqrt2 -> 162.84669170726193 底面の面積:SH=L**2; SH -> 53038.090000000004 ・高さ:H=146.6; 赤道半径R0の比率:R0=6378136.6; R0/H -> 43507.07094133697 ・斜辺長(側面図):c=sqrt(Lh**2+H**2); c -> 186.41642229159962 ・斜面の総面積:Sc4=(L*c/2)*4; Sc4 -> 85863.40410751078 底面に対する面積比:p=Sc4/SH; p -> 1.6189007580686028(≒黄金比) ・直角三角形の3辺の比(側面図): (Lh:H:c)*3/Lh=(3:3.8193660442900557:4.856702274205809) 3辺の比が3:4:5の面積比:p=5/3; p -> 1.6666666666666667(>黄金比) ・傾斜角[deg]:t=rad2deg(atan(H/Lh)); t -> 51.85140476483709 自然の目安:粉体の安息角=15~45[deg] ⇒ 自然の山の傾斜角=15~35[deg] ・Gizaの3大pyramidの面積比:3辺の比:傾斜角 calc_geometry(L,H)=<[ Lh=L/2,SH=L**2,c=sqrt(Lh**2+H**2),Sc4=(L*c/2)*4, ratio=(Lh:H:c)*3/Lh,p=Sc4/SH,t=rad2deg(atan(H/Lh)), =<round((p:ratio:t)*1e3)/1e3 ]=>; 1st:calc_geometry(230.3,146.6) -> (1.619:3:3.819:4.857:51.851) 2nd:calc_geometry(215.29,143.87) -> (1.669:3:4.01:5.008:53.196) 3rd:calc_geometry(105,65.5) -> (1.599:3:3.743:4.797:51.287) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
目次
応力分布 の解釈 |
応力分布の解釈について記述する
pyramidの「重量拡散の間」 ・「重量拡散の間」:「王の間」天井の上方にある5層の部屋空間(各層の天井のみflat) ・最上層のみ:三角屋根の空間 ・目的:「王の間」の空間を圧縮による崩落から保護 ・施工:最上層に三角屋根の空間を設置(「女王の間」は天井が三角屋根) ・効果:上部の重量を真下から横方向に拡散 ・結果:三角屋根の空間の真下は圧縮応力が相対的に低下(間接的に重量を軽減) ・補足:別の用途でない場合、経験的な理解から層を多重化の可能性(効果範囲拡大||fail-safe等) ・余談:当時に共感(時代背景を含む)⇒確度上昇の可能性 自重による垂直応力分布 ・仮定:均質な正四角錐(空隙なし・重心の偏心なし) ・符号なし(通常、軸力が圧縮の場合、応力は負) g=9.8; rho=2500; L=230.3; H=146.6; S(h)=<(L*h/H)^2; V(h)=<_ih(=<S(h),0,h); /*V(h)=<L^2*H/3;*/ m(h)=<rho*V(h); F(h)=<m(h)g; s(h)=<F(h)/(S(h)||1); ・頂点から底面までの深さ方向の垂直応力分布 s(0) -> 0 s(20) -> 163333.33333333337+O(4e-2) s(40) -> 326666.666666667+O(2e-1) s(60) -> 490000.0000000002+O(4e-1) s(80) -> 653333.3333333337+O(6e-1) s(100) -> 816666.6666666674+O(1e+0) s(L/2) -> 940391.6666666666+O(1e+0) s(120) -> 980000+O(1e+0) s(140) -> 1143333.333333334+O(2e+0) s(H) -> 1197233.3333333337+O(2e+0) ・double-check 底面の断面積:S(H) -> 53038.09 総容量:V(H) -> 2591794.664666667+O(5e+0) 総容量:L^2*H/3 -> 2591794.664666666 全自重:m(H) -> 6479486661.666668+O(1e+4) 全重力:F(H) -> 63498969284.33335+O(1e+5) 底面の垂直応力:F(H)/S(H) -> 1197233.3333333337+O(2e+0) ・stressを線形化 s(h)=<1.1972333333333337e6*h/H analogy ・次元Dを定義して、単位blockの断面積=重力=1に正規化、頂上からの段数h=1~に一般化 ns(h)=<_sn(=<n**(D-1),1,h)/h**(D-1) ・4次元の場合 ns(1) -> 1 ns(2) -> 1.125 ns(3) -> 1.3333333333333333 ns(4) -> 1.5625 ns(5) -> 1.8 ns(6) -> 2.0416666666666665 ns(7) -> 2.2857142857142856 ns(8) -> 2.53125 ns(9) -> 2.7777777777777777 ns(10) -> 3.025 ns(100) -> 25.5025 ns(1000) -> 250.50025 ns(10000) -> 2500.500025 ns(99) -> 25.252525252525253 ns(999) -> 250.25025025025025 ns(9999) -> 2500.2500250025 ns(88) -> 22.50284090909091 ns(888) -> 222.50028153153153 ns(8888) -> 2222.5000281278126 ns(77) -> 19.753246753246753 ns(777) -> 194.75032175032175 ns(7777) -> 1944.7500321460718 ns(66) -> 17.00378787878788 ns(666) -> 167.00037537537537 ns(6666) -> 1667.0000375037503 ns(55) -> 14.254545454545454 ns(555) -> 139.25045045045044 ns(5555) -> 1389.2500450045004 ns(44) -> 11.505681818181818 ns(444) -> 111.50056306306307 ns(4444) -> 1111.5000562556256 ns(33) -> 8.757575757575758 ns(333) -> 83.75075075075075 ns(3333) -> 833.7500750075008 ns(22) -> 6.011363636363637 ns(222) -> 56.001126126126124 ns(2222) -> 556.0001125112511 ns(11) -> 3.272727272727273 ns(111) -> 28.25225225225225 ns(1111) -> 278.25022502250226 ・3次元の場合 ns(1) -> 1 ns(2) -> 1.25 ns(3) -> 1.5555555555555556 ns(4) -> 1.875 ns(5) -> 2.2 ns(6) -> 2.5277777777777777 ns(7) -> 2.857142857142857 ns(8) -> 3.1875 ns(9) -> 3.5185185185185186 ns(10) -> 3.85 ns(100) -> 33.835 ns(1000) -> 333.8335 ns(10000) -> 3333.83335 ns(99) -> 33.5016835016835 ns(999) -> 333.50016683350015 ns(9999) -> 3333.5000166683335 ns(88) -> 29.835227272727273 ns(888) -> 296.5001876876877 ns(8888) -> 2963.166685418542 ns(77) -> 26.16883116883117 ns(777) -> 259.5002145002145 ns(7777) -> 2592.8333547640477 ns(66) -> 22.502525252525253 ns(666) -> 222.50025025025025 ns(6666) -> 2222.5000250025 ns(55) -> 18.836363636363636 ns(555) -> 185.5003003003003 ns(5555) -> 1852.1666966696669 ns(44) -> 15.170454545454545 ns(444) -> 148.50037537537537 ns(4444) -> 1481.8333708370837 ns(33) -> 11.505050505050505 ns(333) -> 111.50050050050051 ns(3333) -> 1111.5000500050005 ns(22) -> 7.840909090909091 ns(222) -> 74.50075075075075 ns(2222) -> 741.1667416741674 ns(11) -> 4.181818181818182 ns(111) -> 37.5015015015015 ns(1111) -> 370.8334833483348 ・2次元の場合、組体操の接触面に同様 h 1 _ 2 _ _ 3 _ _ _ 4 _ _ _ _ 5 _ _ _ _ _ 6 _ _ _ _ _ _ 7 _ _ _ _ _ _ _ 8 _ _ _ _ _ _ _ _ 9 _ _ _ _ _ _ _ _ _ ns(1) -> 1 ns(2) -> 1.5 ns(3) -> 2 ns(4) -> 2.5 ns(5) -> 3 ns(6) -> 3.5 ns(7) -> 4 ns(8) -> 4.5 ns(9) -> 5 ns(10) -> 5.5 ns(100) -> 50.5 ns(1000) -> 500.5 ns(10000) -> 5000.5 ・1次元の場合 h 1_ 2_ 3_ 4_ 5_ 6_ 7_ 8_ 9_ ns(1) -> 1 ns(2) -> 2 ns(3) -> 3 ns(4) -> 4 ns(5) -> 5 ns(6) -> 6 ns(7) -> 7 ns(8) -> 8 ns(9) -> 9 ns(10) -> 10 ns(100) -> 100 ns(1000) -> 1000 ns(10000) -> 10000 ・0次元の場合、複素数演算 ns(1) -> 1 ns(2) -> 3 ns(3) -> 5.5 ns(4) -> 8.333333333333334 ns(5) -> 11.416666666666668 ns(6) -> 14.7 ns(7) -> 18.15 ns(8) -> 21.742857142857137 ns(9) -> 25.460714285714293 ns(10) -> 29.289682539682552 ns(100) -> 518.7377517639624 ns(1000) -> 7485.470860550342 ns(10000) -> 97876.06036044357 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 項目 | 内容 |
|---|---|
|
目次
前提 |
外部仕様の前提について記述する
主として数値計算の基本となるCalculatorの仕様とtest caseを記録 説明上の前提を列挙する ・論理記号||は、ORを意味する ・arrow記号->の左側に入力の演算内容、右側に出力の演算結果を示す 入力演算内容 -> 出力演算結果 入力演算内容case1 || 入力演算内容case2 -> 出力演算結果 ・誤差のOrderをLandauの記号O(指数表記1e-16等)で表記する ・vector||行列の成分を要素と表記する ・方程式||関数式を引数に取る関数を高階関数と表記する この場合の引数を通常の値渡しに対して式渡しと表記する 高階関数の束縛変数(bound変数)をdummy変数と表記する ・option引数をopt_変数名で表記する ・原則、SI単位系を使用する test caseの場合、基準値で無次元化される前提で大半の単位を明記しない(公式を除く) ・2項演算子の結合性は左結合で記述する ・除算より記号省略乗算の演算優先で記述する ・行列は本仕様書の構文で記述する ・微分はLagrangeの記法で記述する |
|
目次
変更履歴 |
変更履歴の項目を列挙する
・演算仕様変更履歴 ・演算既定値変更履歴 ・演算仕様廃止履歴 ・演算仕様厳格化履歴 ・機能拡張履歴 ・拡張行列演算拡張履歴 ・演算最適化履歴 ・plot仕様変更履歴 ・plot表示仕様変更履歴 ・pending |
|
目次
演算仕様 変更履歴 |
演算仕様の変更履歴について記述する
演算結果の後方互換性を失う仕様変更/影響項目を列挙する ・Ver.2.31.17以降、変数のscopeを追加 角括弧[] 内部option ・Ver.2.32.17以降、式変数のargumentsを追加 記号省略乗算 ・Ver.2.73.29以降、拡張行列演算を追加 本来、定義できない行列演算 ・Ver.2.79.31以降、列参照と列代入の行index=-1 ⇒ Napier数e Ver.2.76.29以降、列参照 Ver.2.76.29以降、列代入 Ver.2.78.31以降、要素参照の反転機能 Ver.2.78.31以降、要素代入の反転機能 離散Wavelet変換の解法(列代入) strict-mode式変数list ・Ver.2.87.32以降、一部の演算子||関数をPythonに準拠 べき乗演算子**を右結合固定に変更(^演算子は変更なし) 整数商演算子%%を追加(//演算子の代替) 剰余・整数商の演算子のprecedenceを除算||乗算に統合 int関数を0側に丸める仕様に変更(floor関数は変更なし) ・Ver.2.88.32以降、定義できない乗算||減算||加算を拡張行列演算に追加 ・Ver.2.127.34以降、行列sizeの丸め方を変更floor ⇒ round ・Ver.2.146.37以降、接頭辞判定の正規表現を修正 ECMAScript6対応環境の場合、2進数と8進数の接頭辞を追加 ・Ver.2.156.38以降、irregular行列の行列結合の仕様変更 列方向の欠損要素を自動で埋める ⇒ 欠損要素を埋めない(挙動を明確化) strict-mode式変数list等、実用への影響なし ・Ver.2.158.38以降、NaN||論理値literalを追加 論理演算子(短絡評価)のfalse判定値を更新:0 ⇒ 0||NaN 本manualの演算結果を更新:[MyErr] isNaN ⇒ NaNを含む行列 引数不正でfalseを返す一部の実装関数を正常化 Ver.2.162.39以降、NaNを含む演算結果のplot2d出力に対応 ・Ver.2.165.40以降、論理演算子(短絡評価)のfalse判定値を追加更新:0||NaN ⇒ 0||false||NaN 通常の論理演算子の挙動は問題なし(追記のみ) ・Ver.2.168.41以降、論理NOT演算子の仕様変更 operandは実数のみ ⇒ AND||OR同様に、複素数に拡張 ・Ver.2.174.42以降、strict-modeの制約条件を1点追加 strict-mode式変数list等、実用への影響なし ・Ver.2.178.44以降、補間関数のlookup-table標本点の仕様変更 実部と虚部の各keyに対する各value(query困難) ⇒ 実数値keyに対する複素数value strict-mode式変数list等、実用への影響なし ・Ver.2.184.44以降、real自動切替機能を追加 complex ⇒ auto-real selected既定(本manual以前の演算結果は未更新) 後方互換性を維持する場合、complex selected 影響項目:sqrt関数||pow関数||log関数||三角関数||双曲線関数 独自evalの既定値を更新 ・Ver.2.185.44以降、size行列関数の非正方行列の返値の仕様変更 列数n ⇒ {行数m,列数n} ・Ver.2.186.44以降、cmin/cmax関数の関数名を変更 cmin/cmax関数 ⇒ camin/camax関数(manual一括変更) ・Ver.2.186.44以降、cmin/cmax関数の返値の仕様変更 絶対値 ⇒ 要素(統計関数に準拠) strict-mode式変数listへの影響なし ・Ver.2.187.44以降、normr/norm/normc行列関数を追加して返値の仕様変更 最終行/最終列vectorのnorm ⇒ 各行/各列vectorのnorm(正規化行列関数に準拠) strict-mode式変数listへの影響なし ・Ver.2.194.45以降、式変数のargumentsの再帰callに対応 ・Ver.2.195.45以降、式変数のargumentsの無名callに対応 ・Ver.2.196.46以降、最上位関数||演算子代替関数 ||比較演算子||関係演算子||論理NOT演算子||論理XOR演算子の返値の仕様変更 0||1 ⇒ false||true strict-mode式変数listへの影響なし ・Ver.2.205.46以降、整数の丸め方を変更floor ⇒ round(行列sizeの丸め方に準拠) 影響項目:階乗関数||再帰call||gcd/lcm関数||gcd/lcm ||高階関数||高階行列関数の引数(回数||整数範囲||step||次数||分割数) strict-mode式変数listへの影響なし ・Ver.2.219.50以降、式渡し記号=<の仕様を変更して==<を追加 元scopeを維持:=< call先にscope継承:==< 影響項目:solvex_non_linear||FourierN ||scope継承pass||scope継承call||scope継承callの補足 ・Ver.2.222.50以降、命令文を拡張(log表示内容の変更なし) local storage ⇒ static scopes2d array 影響項目:scope_NG||solvex_bisection ・Ver.2.229.56以降、closure機能の仕様変更 式変数のargumentsをscope変数から削除 ⇒ 削除しない 上書き不可の仕様を維持(再帰callの参照透過性を維持) 影響項目:変数のscope||単独scope||式変数への式読出し||explicit ODE_RK4 ・Ver.2.231.56以降、高階関数||高階行列関数の参照透過性対策を実施 dummy変数の変数名symbol:関数名の一部 ⇒ 関数の引数(Ver.2.812.131以降、旧仕様廃止) strict-mode式変数listへの影響なし ・Ver.2.237.56以降、Jacobi高階行列関数||Newton高階行列関数||ODE高階行列関数の第1引数を拡張 列vector形式のみ ⇒ 行||列vector形式を自動判別 Ver.2.776.123以降、ODEt高階行列関数の自動判別を追加修正(最小要素数のみ) _t(=<{__t__},,=<{,},1,1) -> (1:0.5+O(1e+0)) _t(=<{__t__},,=<(,),1,1) -> ・Ver.2.240.56以降、行列関数の既定形式の仕様変更(一般的な言語に準拠) reshape:reshapec ⇒ reshaper(列vector形式 ⇒ 行vector形式) 影響項目:reshape行列関数||norm行列関数||正規化行列関数||solveAinv ・Ver.2.253.59以降、直接式読出しの仕様変更 返却時の式読出し記号=>省略可 ⇒ 省略不可(省略時、変数のみ判別) 影響項目:直接式読出し||template ・Ver.2.254.59以降、$let宣言の再代入の仕様変更(初回のみ、$あり ⇒ 常時、$あり) ・Ver.2.268.62以降、最上位関数のvar||eqnを統合 影響項目:最上位関数||strict-mode式変数list ・Ver.2.290.71以降、式変数のargumentsのscope変数保持条件の仕様変更 保持条件:無条件 ⇒ 式変数が未解決(右代入を含む) 影響項目:式変数のargumentsの動的判別@Non-strict-mode clear; f=(g)=<g; f(1),f((x)=<x) -> ・Ver.2.291.71以降、scope変数のsearch-precedenceの仕様変更 変数||式変数のsearch-precedence:全階層 ⇒ 階層毎 影響項目:search-precedence||useMutex clear; f=<-1; f=1; [f=2,=<f]=>,[f=<-2,=<f]=> -> (2, ・Ver.2.299.72以降、変数のscopeの仕様変更 static scopes2d arrayを共有 ⇒ 動的に確保して解決済みの場合、削除 block-scope:id_treeのfiltering継続 影響項目:strict-mode||変数のscope||単独scope ||scope_NG||curried||counter ・Ver.2.343.83以降、scope参照の仕様修正 変数への代入時に右辺の参照を削除しない ⇒ 削除する strict-mode式変数listへの影響なし Ver.2.346.85以降、行列要素pattern matching||式変数への代入時も同様に、右辺の参照を削除 影響項目:Call-by-Reference(式変数make_NG部分のみ) ・Ver.2.369.86以降、精度次数が存在する高階関数の仕様変更 精度次数:固定 ⇒ 関数名直後の数字で指定可(内部optionより優先) Ver.2.774.119~2.775.121以降、ODE高階行列関数のadaptive-step solverを追加 Ver.2.776.122以降、ODE高階行列関数を任意のButcher-table入力で再実装(Machine epsilonの後方互換性) Ver.2.777.123以降、同上の外部入力に対応 _o() ⇒ _o||_o4||_o2||_o5||_o45||_o3||_o23||_o1()||_o12||_o0() _t() ⇒ _t||_t4||_t2||_t5||_t45||_t3||_t23||_t1()||_t12||_t0() _d() ⇒ _d||_d4||_d2() _i() ⇒ _i||_i4||_i2() 影響項目:微分高階関数||積分高階関数||ODE高階行列関数||ODEt高階行列関数 ・Ver.2.381.86以降、繰り返し回数=1~のdummy変数を一時的に保持する予約変数__n__を追加 影響項目:再帰高階関数 ・Ver.2.444.90以降、Graphing Calculatorのt0/t1分割点の丸め方を最適化(Machine epsilon程度の相違あり) space初期化行列関数同様の最適化@Ver.2.228.55:t0+(t1-t0)*(n/N) ⇒ t0+((t1-t0)/N)*n 影響項目:t0/t1||plot2d ・Ver.2.721.101以降、mod関数と冗長なfmod関数の仕様変更 剰余演算子とmod関数に同義 ⇒ 常に正の余りを返す 影響項目:fquot関数を追加 strict-mode式変数listへの影響なし ・Ver.2.736.107以降、予約変数__t__||__x__を追加 影響項目:ODE高階行列関数||ODEt高階行列関数 ・Ver.2.739.107以降、予約変数__x__に追加の対応 影響項目:Jacobi高階行列関数||Newton高階行列関数 ・Ver.2.791.126以降、symbol渡し||name渡しの仕様修正 重複宣言:可 ⇒ 不可 影響項目:式変数のarguments ・Ver.2.833.140以降、代入処理の挙動を統一@Non-strict-mode symbol渡しの自動展開:なし ⇒ あり clear; f(x)=<d=x:[($a)=(=<f/*Non-strict-mode*/),b=(=<f),c=[],c.push(=<f),[a,b,c]] -> clear; c=[],c.push(=<f) -> [MyErr]Undef eqn(f) 影響項目:symbol渡し||push clear; f(x)=<d=x:[($a)=(==<f/*Non-strict-mode*/),(a)(1)=>,hass(d)],hass(d) -> (0:0,0,false,true) clear; f(x)=<d=x:[b=(==<f),(b)(1)=>,hass(d)],hass(d) -> (0:0,0,true,false) clear; f(x)=<d=x:[c=[],c.push(==<f),(c)(1)=>,hass(d)],hass(d) -> (0:0,NaN,0,true,false) ・Ver.2.857.158以降、微分高階関数の第2と第3の引数順序の交換と仕様変更 第2引数の省略:可 ⇒ 不可 影響項目:微分高階関数||MaclaurinN||TaylorN ・Ver.2.858.159以降、積分高階関数の仕様変更 N=0の返値:N=100の演算結果 ⇒ 初期値0 ・Ver.2.858.159以降、ODE高階行列関数||ODEt高階行列関数の引数の仕様変更(積分高階関数に準拠) 第4||3引数:時間刻み ⇒ dummy変数終了値(省略不可) 第5||4引数:省略時、1 ⇒ NI既定値 影響項目:ODE高階行列関数||ODEt高階行列関数||strict-mode式変数list ・Ver.2.871.164以降、Gaussの消去法のpivot選択の処理順の致命的な不具合を修正 処理順:前進消去の直前 ⇒ 前進消去の各step 効果:Newton高階行列関数のretry機能の問題を解消 影響項目:Newton高階行列関数||solvex_Gauss||solvex_pivotting |
|
目次
演算既定値 変更履歴 |
演算既定値の変更履歴を列挙する
・Ver.2.321.78以降、差分刻みの仕様修正(修正量ではなく、絶対値 ⇒ 微分位置の相対値) 微分位置xでの差分刻みdx既定値:max(1,abs(x))dx(1+i) ⇒ dx((real(x)||1)+(imag(x)||1)i) 影響項目:微分高階関数||Jacobi高階行列関数||Newton高階行列関数 ||solvex_iteration||solveAinv||solvex_non_linear||solvex_bisection ||implicit Euler_method||explicit Euler_method ・Ver.2.835.141以降、差分刻みの内部option既定値を修正 浮動小数点演算:10進形式 ⇒ 2進形式 epsN:1e-16 ⇒ Machine epsilon dxJ:1e-5 ⇒ 2^(-16) dxD:1e-3 ⇒ 2^(-10) Newton((x)=<2x+1=0) -> 影響項目:微分高階関数||Jacobi高階行列関数||Newton高階行列関数||Newton法||strict-mode式変数list ・Ver.2.858.159以降、dxTを廃止 ・Ver.2.864.160以降、分割数の内部option既定値を修正 浮動小数点演算:10進形式 ⇒ 2進形式 NI:100 ⇒ 2^7 _i((x)=<x**2,0,3) -> 影響項目:積分高階関数||ODE高階行列関数||ODEt高階行列関数 ||plot2d_evolution||residue||heat1d_evolution |
|
目次
演算仕様 廃止履歴 |
演算仕様の廃止履歴を列挙する
・Ver.2.203.46以降、変数への式読出しの仕様を廃止して式変数への式読出しを追加 読出し値が残る唯一の仕様 ⇒ 読出し値が残る仕様を撤廃 影響項目:strict-mode||plot2d-from-arr||plot2d_circle||式読出し||代入処理 ・Ver.2.234.56以降、高階関数||高階行列関数の参照透過性対策を完了 scope変数を参照、上書きする ⇒ scope変数から独立する(引数のみ有効) 影響項目:plot2d_evolution||solvex_iteration||solveAinv||solvex_non_linear||solvex_bisection ||implicit Euler_method||explicit Euler_method||explicit ODE_RK4||heat1d_evolution heat1d_evolutionのみ、Newton法の初期値をscope変数から継承しないため、演算結果が変わる ・Ver.2.253.59以降、引数省略callの仕様廃止(式変数のargumentsの判別を厳格化) 影響項目:strict-mode ・Ver.2.253.59以降、式変数の新規複製の仕様廃止 影響項目:式変数への式読出し||args||solvex_bisection ・Ver.2.747.112以降、列参照と列代入の初期仕様廃止 A=(1,2:3,4); A[e][0] -> A=(1,2:3,4); A[][0] -> (1:3) 影響項目:行列への参照||行列への代入 ・Ver.2.812.131以降、高階関数の旧仕様廃止 dummy変数の変数名symbol:関数名の一部 ⇒ 関数の引数(Ver.2.815.132以降、引数のerror処理を強化) 影響項目:高階関数||strict-mode式変数list ・Ver.2.813.131以降、symbolic高階行列関数の仕様廃止(Ver.2.736.107~2.739.107以降、冗長) _e() ⇒ 予約変数__x__とreshape行列関数 影響項目:strict-mode式変数list(Ver.2.815.131以降、heat1d_evolutionのみ、数値解を変更) ・Ver.2.816.132以降、高階行列関数の第2引数を廃止(左詰めで第1引数に統合) 影響項目:高階行列関数||strict-mode式変数list ・Ver.2.830.139以降、method演算子のunshift/push()の遅延評価を廃止(Ver.2.829.139以降、無駄仕様) 引数の遅延評価:あり ⇒ なし(式渡しの判別) 影響項目:method演算子||strict-mode式変数list ・Ver.2.857.158以降、微分高階関数の参照透過性対策を完了 scope変数を参照する ⇒ scope変数から独立する(引数のみ有効) 影響項目:MaclaurinN||TaylorN |
|
目次
演算仕様 厳格化履歴 |
演算仕様の厳格化履歴を列挙する
・Ver.2.210.46以降、単独scopeの判定を厳格化(scope_NGのNG範囲を最小化) 式の長さ制限あり ⇒ 長さ制限なし(単独の括弧を探索) 影響項目:scope付式変数の再利用||scope_NG ・Ver.2.272.63以降、空括弧の判別を厳格化 無条件に削除 ⇒ 定数()のみ削除・波括弧{}禁止 ・Ver.2.272.63以降、引数0個の関数callを厳格化 丸括弧()の省略可 ⇒ 省略不可 影響項目:乱数関数||random||magic-square ・Ver.2.275.65以降、既定で式変数のcall記号省略不可(syntaxの問題を解消) call記号:=> ⇔ 関数callの丸括弧() 記号省略:自動実行 ⇒ 式変数宣言@Non-strict-modeの判別(callの場合、記号を明示) last{set_x=<(x=1),x=0,set_x,x} -> last{set_x=<(x=1),x=0,set_x(),x} -> 1 syntaxの問題:下記arguments無効で実行可能 ⇒ error終了 _r((n)=<run,run(n,n)=<n+1,3) -> _r((n)=<run(),run(n,n)=<n+1,3) -> [MyErr]Invalid args.length=2(run) _r((n)=<run(),run=<n+1,3) -> 3 影響項目:Non-strict-mode||高階関数||高階行列関数 ・Ver.2.290.71以降、丸括弧()の判別を厳格化 =<x,()=<x -> ($x, =<x+1,()=<x+1 -> (eqn,eqn()) (x)=<x,(x,y)=<x+y -> (eqn(x),eqn(x,y)) {x,y}=<x+y,{(x,(y,z))}=<x+y+z -> (eqn(y),eqn(x,y,z)) ・Ver.2.301.72以降、escape記号を予約語に追加 $記号:変数名symbolの一部に使用可 ⇒ 使用不可 影響項目:変数の命名規則 ・Ver.2.373.86以降、行列size指定のindexを厳格化 index:[0] ⇒ 空行列[]([0]指定の場合、初期化と異なり、size不正のerror終了) 影響項目:area参照||area代入 ・Ver.2.421.88以降、行列への代入の行列size比較を厳格化 行代入:右辺の最終行を代入 ⇒ 1行の場合、代入可 列代入:右辺の最終列を代入 ⇒ 1列の場合、代入可 要素代入:右辺の最終要素を代入 ⇒ 1要素の場合、代入可 影響項目:行代入||列代入||要素代入 ・Ver.2.440.90以降、行列要素pattern matchingの行列size比較を厳格化 行列size違いの比較可 ⇒ 比較不可 影響項目:行列要素pattern matching clear; ($a,$b,$c)=(1,2); (a,b) -> ・Ver.2.441.90以降、行列要素pattern matchingの要素比較を厳格化 代入に無関係の要素の比較可 ⇒ 比較不可 影響項目:行列要素pattern matching clear; ($a,$b,3)=(1,2,=<4); (a,b) -> ・Ver.2.735.105~107以降、高階行列関数の引数判定を厳格化 引数省略:引数不足の場合、error終了 _t(=<1) -> Ver.2.774.121以降、ODEt高階行列関数の引数判定を追加修正 _t(=<1,,,1,1) -> 引数の行列size比較:size不整合の場合、error終了 _o((t,x)=<t,,=<{,,},,1,4) -> 初期値省略:無次元の0以外の場合、error終了 _o((t,x)=<t,,true,,1,4) -> _t((t,x)=<t,,true,1,4) -> Newton((x)=<x+0,1,true) -> Ver.2.843.149以降、size不整合の判定を厳格化 _o((t,x,y)=<(,),=<{,},1,1) || _o((t,x,y)=<{,},=<(,),1,1) -> [MyErr]Invalid OX arguments(RC) _t((t,x,y)=<(,),=<{,,},1,1) || _t((t,x,y)=<{,},=<(,,),1,1) -> [MyErr]Invalid TX arguments(RC) Jacobi((x,y)=<(x,y),=<{,})|| Jacobi((x,y)=<{x,y},=<(,)) -> [MyErr]Invalid jacobian arguments(RC) Newton((x,y)=<(x,y),=<{,})|| Newton((x,y)=<{x,y},=<(,)) -> [MyErr]Invalid newtonian arguments(RC) ・Ver.2.747.112以降、行列indexの判別を厳格化 A=(1,2:3,4); A[i] -> 影響項目:行列への参照||行列への代入 内部判定値:Math.E ⇒ null ⇒ undefined Ver.2.768.117以降、error終了を復帰 A=(1,2:3,4); A[][] -> A=(1,2:3,4); A[][][] -> A=(1,2:3,4); A[][][][] -> |
|
目次
機能拡張履歴 |
機能の拡張履歴を列挙する
・Ver.2.255.59以降、行列への参照から式変数への式読出しに対応 ・Ver.2.257.59以降、iterator演算子のiterator対象を拡張 iterator対象:変数 ⇒ 変数・式変数 ・Ver.2.258.60以降、論理演算子(短絡評価)||論理演算子(literal)のoperandを拡張 operand:変数 ⇒ 変数・式変数 ・Ver.2.269.62以降、行列要素pattern matchingの遅延評価に対応 変数:要素の値代入のみ ⇒ 式変数のargumentsとの互換性を確保(未解決の場合、error終了) ・Ver.2.271.62以降、再帰高階関数の初期値(第2引数)の遅延評価に対応 ・Ver.2.276.65以降、式変数のargumentsの動的判別@Non-strict-modeに対応 動的判別対象:記号=<の有無||遅延評価の明示 定義元:記号=<を省略不可 ⇒ 省略可(call先の引数を自動展開時、付与のflagからtree継承) call先:省略可(遅延評価の明示を除く) ・Ver.2.277.65以降、equal記号=の動的判別に対応(行列への参照||再利用を含む) 動的判別対象:記号=<の有無 equal記号=:省略の前提 ⇒ 省略可(旧仕様を含めて統廃合の可能性あり) ・Ver.2.279.65以降、iterator演算子の第1引数の動的判別@Non-strict-modeに対応 動的判別対象:記号=<の有無 実装関数の引数:動的判別なし ⇒ iterator演算子@Non-strict-modeのみ対応 ・Ver.2.282.66以降、式変数のargumentsの判別対象を拡張 遅延評価の明示対象:式変数宣言を除く ⇒ 式変数宣言を含む clear; f=(A)=<A; f(=<(1,2))=> -> (1,2) clear; A=((x)=<x); (A[0][0])(2)=> -> 2 clear; A_lazy=((x)=<x); f(A)=<(A[0][0])(2)=>; f(=<A_lazy)=> -> ・Ver.2.283.66以降、式変数のargumentsの動的判別@Non-strict-modeの参照透過性を対策 clear; f=(h)=<h(3); g=(x)=<x; f(g) -> 3 clear; f=(h)=<h(3); f((x)=<x) -> ・Ver.2.283.67以降、式変数のargumentsの参照透過性の不具合を修正 変数への代入可能判定:数値のみの行列 ⇒ 数値||式変数宣言の行列 A_iterable=(=<1,=<2:=<3,=<4); A_iterable.map((f)=<f()) -> (1,2:3,4) f=(A_iterable)=<[=<A_iterable.map((f)=<f())]=>; f(=<A_iterable) -> (1,2:3,4) f(=<(=<1,=<2:=<3,=<4)) -> ・Ver.2.288.70以降、式変数宣言のlog表示を変更 式変数宣言のlog表示:BTe ⇒ $symbol || eqn || eqn(args) =<x -> [MyErr]Invalid BTe([object Object]) ・Ver.2.296.72以降、const宣言のlog表示に対応(右代入を除く) clear; $a=1 -> const a=1 clear; $f=<1 -> stored_eqn(const f) clear; $f=()=<1 -> stored_eqn(const f) clear; [()=<1]=>$f -> 0 ・Ver.2.298.72以降、変数のprototype method代替のmethod演算子を追加 ・Ver.2.303.73以降、scope変数のscope参照の仕様追加(未最適化) 参照渡し記号:?symbol ・Ver.2.823.135以降、式変数のargumentsの直列化に対応 Ver.2.824.138以降、列方向の欠損要素に対応 h(a,b:c)=<(a,b,c); h(1,2,3):h(1,2:3):h(1:2,3):h(1:2:3) -> (1,2,3:1,2,3:1,2,3:1,2,3) h(a:b,c)=<(a,b,c); h(1,2,3):h(1,2:3):h(1:2,3):h(1:2:3) -> (1,2,3:1,2,3:1,2,3:1,2,3) 定義元とcall先の対応関係:最終行vector ⇒ reshaper行列関数で直列化の行vector 補足:直列化≠行列要素pattern matching 影響項目:式変数のarguments Ver.2.823.136~2.823.137以降、高階行列関数の第2引数のerror処理を強化 f(x,y)=<{,}; Newton(=<f,=<{1,2:3}) -> f(x,y)=<{,}; Newton(=<f,(x)=<{1,2:3}) -> f(x,y)=<{,}; g(x)=<{1,2:3}; Newton(=<f,=<g) -> [MyErr]Invalid newtonian arguments Ver.2.823.137以降、再帰高階関数の第4引数のerror処理を強化 _r((n)=<n+1,,10,(x)=<false) -> h(x)=<false; _r((n)=<n+1,,10,=<h) -> ・Ver.2.829.139以降、method演算子のunshift/push()を拡張(行列結合より高速) 第1引数:行vector ⇒ 行列 影響項目:method演算子 |
|
目次
拡張行列演算 拡張履歴 |
拡張行列演算の拡張履歴を列挙する
・関数の引数vectorの場合 最終行vector ⇒ Ver.2.73.29以降、各行vectorに拡張 ・演算子のoperandの場合 最終行vector ⇒ Ver.2.73.29以降、各行vectorに拡張(comma演算子を適用) ⇒ Ver.2.74.29以降、各要素に拡張(comma演算子使用を選択可) ・Ver.2.88.32以降、定義できない乗算||減算||加算を拡張対象に追加 |
|
目次
演算 最適化履歴 |
演算の最適化履歴を列挙する
・Ver.2.142.36以降、parse段階で実数値の大規模csv-format入力に対応 ・Ver.2.144.36以降、operation段階の行列結合を含むdepthMax制限を追加(browser crashの2重対策) ・Ver.2.156.38以降、operation段階の行列結合のnestingを最適化 区切り文字間に括弧が存在しない場合、部分的にsliceして結合(nestingの多重化を事前に回避) ⇒ 動的memory使用量の低減 ⇒ depthMax制限の余裕確保 ・Ver.2.160.38以降、deep-copyの適用対象を最適化 適用対象:行列結合由来を含む全nesting ⇒ 高階関数||高階行列関数の反復処理由来のnesting ⇒ 動的memory使用量の低減 ⇒ 行列結合を含む演算の高速化 ・Ver.2.202.46以降、deep-copyの適用対象を厳格化(式読出し由来を除外) ・Ver.2.209.46以降、式渡しの実装を最適化 式変数名symbolを含む処理範囲の厳格化(Ver.2.213.49以降、処理範囲を訂正) (0=<3)=> -> [MyErr]Invalid operation ・Ver.2.212.46以降、演算実行確定1回毎にtreeの走査対象を最適化 走査対象:全tag名 ⇒ 使用tag名のみ(Ver.2.212.47以降、必須tagのBT1を追加修正) ⇒ 使用tag名のみ(Ver.2.214.50以降、式変数の再利用を追加修正) ・Ver.2.228.55以降、space初期化行列関数の整数の丸め方を最適化 影響項目:plot2d_interp ・Ver.2.230.56以降、変数名symbolの内部取得関数を最適化 Ver.2.251.58以降、symbol渡しの判定を修正 clear; a=3,f(=<g)=<g(a)=>,f((x)=<x)=> -> clear; a=3,f(=<g)=<g(a)=>,f((x)=<x+1)=> -> (0,0,4) clear; a=3,f((args)=<g)=<g(a)=>,f((x)=<x+1)=> -> Ver.2.252.59以降、式変数のargumentsのerror処理を修正 clear; f(3,x)=<x; f(3,3)=> -> [MyErr]Invalid args.length=0(f) clear; f(3,x)=<x -> [MyErr]Invalid args isFound(f) ・Ver.2.231.56以降、高階関数の内部wrapper関数を追加 ・Ver.2.233.56以降、高階行列関数の内部wrapper関数を追加 ・Ver.2.266.62以降、deep-copyの適用対象を最適化 適用対象:変数・式変数のstore||restore時 ⇒ restore時(予約変数ansを含む) 2重clone:あり ⇒ なし ・Ver.2.284.67以降、式変数のarguments解決の処理を最適化 tree継承flagの保存:変数・式変数のrestore時 ⇒ store時 Ver.2.280.66以降、未定義の変数をoperation段階で検知の影響:重複判定の処理を削除 ・Ver.2.286.67以降、Ver.2.212.46の追加更新 使用tag名判定用のobject初期化処理:instance毎 ⇒ 関数call毎 影響範囲:実行確定1回毎に、instanceを作るため、影響なし(独自evalを含む) ・Ver.2.389.86以降、parse段階のpattern matching処理を最適化 対象:統計関数||高階関数||高階行列関数 内容:tokenの1文字目のunderscore_を判定して高階関数||高階行列関数と統計関数の処理を切替 ・Ver.2.768.116以降、行vectorの列参照を最適化 転置処理:あり ⇒ なし ・Ver.2.844.152以降、Newton高階行列関数の最適化 Jacobi行列の配列初期化:反復の毎step ⇒ 反復前(最初のみ) treeの代入:反復の前後 ⇒ 反復後(最後のみ) |
|
目次
plot仕様 変更履歴 |
Graphing Calculatorのplot仕様変更履歴を列挙する
・Ver.2.33.17以降、正式release 後方互換性のため、内部optionを追加 ・Ver.2.86.32以降、plot範囲を微調整 ・Ver.2.190.44以降、plot範囲の自動調整機能を削除してplot2d-Verの選択肢を追加 Ver.0:Ver.2.33.17以前の仕様(oldPlot2d=true) Ver.1:Ver.2.33.17~2.190.44の仕様 Ver.2:Ver.2.190.44~の仕様 ・Ver.2.277.65以降、式変数宣言のparser-post処理を変更 error終了 ⇒ BTe(BrackeTeqn)のlog表示 ・Ver.2.279.65以降、空括弧のplot値を変更 0 ⇒ 欠損値 ・Ver.2.279.65以降、数値以外の要素(式変数宣言を含む)が残存する場合、plotの挙動を変更 error終了 ⇒ 欠損値に変換 ・Ver.2.280.66以降、上記変更により、未定義の変数を検知不能の致命的な不具合を修正 検知段階: clear; last{a,1} -> 影響項目:size行列関数 ・Ver.2.319.77以降、v入力仕様の仕様変更 vx入力:legend1番で共通 ⇒ 各legendで独立(vy入力に準拠) ・Ver.2.321.77以降、matSizeMaxの既定値を変更 matSizeMax既定値:1000 ⇒ 1024 影響項目:Graphing Calculator||初期化行列関数 ・Ver.2.723.102以降、svg出力のpolylineのmasking不具合を暫定修正 内容:line||polyline単体でblockの場合、意図しないmaskingが稀に発生(line消滅) 前者:未遭遇 後者の対策:<polyline points="" /> ⇒ <polyline points="" /><line /> 再現条件の備考:<polyline />の追加は効果なし ・Ver.2.821.135以降、plot座標から変換後のcanvas座標が無限大の場合、致命的な不具合を修正 内容:canvas座標が無限大の場合、予期せぬerror終了からdeadlockが発生 対策: ・canvas座標が有限を保証するwrapper関数の追加 Ver.2.847.155以降、Infinity判定の厳密化:!(isFinite(x)) ⇒ Math.abs(x) === Number.POSITIVE_INFINITY ・内部関数名の変更を伴うtry~catch処理の大幅修正 ・lock処理の見直し ・Ver.2.843.151以降、plot2d-from-logの区切り文字とdot演算子の記号衝突を訂正 tokenの区切り文字:' ⇒ ["]{1,2} 影響項目:plot2d-from-log||dot演算子 |
|
目次
plot表示仕様 変更履歴 |
Graphing Calculatorのplot表示仕様変更履歴を列挙する
・Ver.2.746.111以降、checkboxの仕様改善 p-checkbox:checkedで全表示 z-checkbox:checked時、z入力欄を有効化 ・Ver.2.759.115以降、自動描画refreshの頻度を変更 refresh頻度:最大10回 ⇒ 最短1秒間隔 影響項目:gradation特定項目仕様 ・Ver.2.770.117~2.773.118以降、grid-layerの数字label表示を改善 丸め方:なし ⇒ 整数以外の場合、Machine epsilonを丸める |
|
目次
pending |
pending項目を列挙する
実装 ・symbol明示記号 ・const代替記号(name渡しと重複の$記号から変更の可能性あり) ・scope不定の式変数のargumentsのuse$let対応(name渡し||scope参照を除く) ・arr=arr|||[] undef宣言未実装 ・[0] -> 0の演算 単独要素の場合、無条件のerror終了 ・__args__ plot ・vz入力欄:tarr_z absolute||argument||vector||contourの選択肢を追加 ・aspect比固定option(round-off桁数との整合性を含む) ・shared storageの双方向化 ・plot点数の間引き処理 debugger ・空行列のerror終了判定強化(高階行列関数を含む) code整理 ・比較判定対象のべた書き ・error処理 ・error-logの内容 最適化 ・非線形方程式の解法 高速化 ・再帰callのtag名 ・再帰callのmemo化option String(引数)と結果のlist優先の短絡評価 仕様廃止 ・右代入 Ver.2.279.65以降、冗長 Ver.2.441.90以降、行列要素pattern matchingの要素比較を厳格化 ・特殊仕様関数(関数名に引数の一部を含む仕様) 仕様見直し ・欠損要素 -(1,2:3) -> (-1,-2:-3,0) ・空行列 []+[] -> [] ・高階行列関数の引数=0で省略判定(初期値の数値入力不可) ・末尾return 仕様変更 ・eqn表記 ⇒ fn表記 参照と区別 ・use$let既定 ・band参照の返値 返値の列vector:上詰め(行indexの維持より転置の対称性を優先) 仕様拡張 ・Gauss(A,b)の行vector入出力に対応(高階行列関数と異なり、代数学に準拠) closed ・式変数のcall記号省略時の挙動 Ver.2.275.65以降、式変数宣言@Non-strict-modeの判別(callの場合、記号を明示) ・has($x) ⇔ has(x)||has(=<x) Ver.2.295.71以降、error終了 has($x) -> $$=1 -> [MyErr]Invalid symbol ・Ver.2.298.72以降、変数のprototype method代替のmethod演算子を追加 A.unshift/push(val,opt_i) unshift:len=sizer(A),opt_i==-(len+1)&&&(A=(val:A))||||last{is=(opt_i||0)%len,A[is]=(val,A[is])} push:len=sizer(A),opt_i==len&&&(A=(A:val))||||last{ie=(opt_i||len-1)%len,A[ie]=(A[ie],val)} ・高階関数の引数順序 ・Ver.2.774.119以降、ODE高階行列関数のadaptive-step solverを追加 ・Ver.2.847.153以降、行列の厳密等価||不等価演算子を追加 ・Ver.2.857.158以降、微分高階関数の第2引数の省略不可(参照透過性の問題を解消) |
|
目次
開発環境 |
JavaScriptのinterpreterを介してbrowser上で演算を実行する
・以降、JavaScript標準規格のECMAScriptをNativeと表記する 開発環境を列挙する ・Microsoft windows 10 ・Google Chrome Developer Tools(以降、Chrome DevToolsと省略する) ・Apache HTTP Server ・GitHub Desktop ・GitHub Pages commit E-mail addressを変更する場合(参考) ・Git Bash(first-commit前にgit config user.emailで設定を変更する) |
|
目次
動作test環境 |
browserの動作test環境について記述する
localhost offline/online-test環境 ・latest Chrome ・latest Edge ・Internet Explorer 11(以降、IEと省略する) ・Ver.2.38.18以降、latest Firefox ・その他、Chrome DevTools-emulatorで動作確認 実機online-test環境 Ver.2.84.32以降、test未実施 ・latest Amazon Silk ・Ver.2.37.18以降、latest Chrome ・Ver.2.38.18以降、latest Firefox |
|
目次
実機 online-test 手順 |
実機mobile端末のonline-test手順について記述する
Ver.2.37.18以降、実機online-testのcommit前実施に対応 ・GitHub Pages上で実施していた実機testの大半を以下の手順でcommit前に実施する ・さらに、今後のapplication開発で必要な実機online-testのdebug環境を整備する 実機online-testのcommit前実施準備を以下に示す ・localhost Apache HTTP ServerのDocumentRootのaccess制限を設定する Require all denied Require ip 192.168. ・localhost Apache HTTP Serverを再起動して設定変更を反映する 実機online-testのcommit前実施手順を以下に示す ・localhostのWi-Fi接続先propertyのnetwork profileを確認する ・localhost Firewallの設定でApache HTTP Serverのprivate||publicを許可する ・localhostと実機を同一のWi-Fiに接続する ・localhost IPv4 addressを確認する ・実機browserのURLにlocalhost IPv4 addressを入力して更新する ・localhost Apache HTTP ServerのDocumentRootからの相対pathでtestするpageを開く ・以上より、Wi-Fiを介して実機online-testを実施する ・test終了後、必要に応じてlocalhost Firewallの設定を元に戻す さらに、localhost Chrome DevToolsでAndroid端末を操作してdebugする手順を以下に示す ・Android端末のBuild numberを7回tapしてDeveloper optionsを表示する ・System-Advanced-Developer optionsを開く ・USB debuggingを有効化する ・Android端末をlocalhostにUSB接続してUSB debugging connectedを確認する ・localhost ChromeのURLにchrome://inspect/#devicesを入力して更新する ・Android端末に表示されるcomputer's RSA keyによる接続を許可する ・先述の実施手順に従ってAndroid端末Chromeでlocalhostのdebugするpageを開く ・localhost Chromeに戻ってAndroid端末情報を確認する ・debugするpage URLのinspectを実行して新しいwindowを開く ・Chromeの同一page上でlocalhostとAndroid端末の操作が連動することを確認する ・以上より、Wi-Fiを介して実機online-testとともにdebug(Single-threadが基本)を実施する ・test終了後、必要に応じてAndroid端末の設定を元に戻す |
|
目次
download 手順 |
download手順について記述する
各pageのlinkからfileのdownload手順を以下に示す ・pageのload完了 ・content生成 ・linkをdouble-click||tap 留意事項を列挙する ・browser上でcontentを生成するため、data通信なし(offlineでdownload可) ・UI設定と生成用script||plot2d-commandを共有すれば同じcontentを再現可能(生dataの通信不要) |
|
目次
動作要件 |
browserの動作要件を列挙する
・ECMAScript5対応 ・HTML5対応 |
|
目次
動作環境依存 |
browserの動作環境依存について記述する
最新のECMAScript6対応環境(内部で自動判定)で動作する機能/影響項目を列挙する ・Ver.2.146.37以降、2||8進数literalに対応 Simple Calculator's 0b||0o-button(非対応環境の場合、非表示) |
|
目次
browser間 の相違 |
browser間の相違について記述する
png||svg出力の相違について記述する ・browserによってtext幅のNative測定値が異なる var text = "x=t,x;x"; ctx.font = "10px sans-serif"; var w = ctx.measureText(text).width; IE: w -> 29 Edge/Chrome: w -> 36.2841796875 Firefox: w -> 30 ctx.font = "12px sans-serif"; var w = ctx.measureText(text).width; IE: w -> 35 Edge/Chrome: w -> 43.541015625 Firefox: w -> 31 ・Edge/Chromeはpngとsvgの出力表示が一致するが、IE/Firefoxは一致しない JavaScript engineの系統による違いと推察されるが、規則性が不明で対応未定 ・textを除けばbrowser間の出力表示に大差なし 演算結果の相違について記述する ・browser間でMachine epsilon程度の相違がある IE: sin(5) -> -0.9589242746631384 Edge/Chrome/Firefox: sin(5) -> -0.9589242746631385 IE/Edge/Chrome: exp(i) -> 0.5403023058681398+0.8414709848078965i Firefox: exp(i) -> 0.5403023058681397+0.8414709848078965i |
|
目次
Internet Explorer 非対応の機能 |
IE非対応の機能について記述する
IE非対応の機能/原因を列挙する ・bg-image-file 描画更新時、SCRIPT5022: SecurityError |
|
目次
ECMAScript との相違 |
ECMAScriptとの相違について記述する
明確な相違点を列挙する ・括弧の演算のprecedence(式変数||関数callより優先) 括弧の中身を自動展開(行列を想定)するため、遅延評価の場合、記号=<を明示 ・arrow関数 ECMAScript6 f=(x)=>x; g=(h,x)=>h(x)*x; g((x)=>g((x)=>f(x),2),2) -> 8 本仕様(遅延評価と名前衝突||単独scopeに留意) f=(x)=<x; g=(=<h,x)=<h(x)*x; || g=(=<f,x)=<[=<f(x)*x]=>; g((x)=<g((x)=<f(x),2),2) -> 8 ・論理演算子(短絡評価) ECMAScript6 fibo_=(n)=>n<2&&n||fibo_(n-1)+fibo_(n-2); fibo_(10) // NG -> -47 本仕様 fibo_=(n)=<n<2&&n|||fibo_(n-1)+fibo_(n-2); fibo_(10) // NG -> -47 ・中置3項演算子 ECMAScript6 fibo_=(n)=>((n<2)? n: fibo_(n-1)+fibo_(n-2)); fibo_(10) // OK -> 55 本仕様(論理演算子(literal)で代替) fibo_=(n)=<n<2&&n||||fibo_(n-1)+fibo_(n-2); fibo_(10) // OK -> 55 ・無名再帰 ECMAScript6 (fact_=(n)=>n<=1||n*fact_(n-1))(10) -> 3628800 本仕様(無名call||代入処理参照) ([fact_=(n)=<n<=1|||n*fact_(n-1),=<fact_]=>)(10)=> -> 3628800 明確に冗長な仕様を列挙する ・式変数 ・記号省略乗算 ・無名callのcall記号=>(記号省略乗算と区別するため、省略不可) ・scope継承 |
|
目次
Excel との相違 |
Excelとの相違について記述する
明確な相違点を列挙する ・前置単項演算子の符号のprecedence -1^2 || -(1^2) -> -1 3+-3 -> [MyErr]Invalid binary operation 2^-1 -> [MyErr]Invalid binary operation 3+(-1) -> 2 2^(-1) -> 0.5 ・log関数の底 log(10) -> 2.302585092994046 log_ex(10) -> 1 ・atan2関数の引数順序 atan2(1,0) -> 1.5707963267948966 atan2_ex(1,0) -> 0 |
|
目次
Python との相違 |
Pythonとの相違について記述する
明確な相違点を列挙する ・前置単項演算子の符号のprecedence 3+-1 -> [MyErr]Invalid binary operation 2**-1 -> [MyErr]Invalid binary operation 3+(-1) -> 2 2**(-1) -> 0.5 ・虚数単位の記号 3+1j -> [MyErr]Invalid ans isFound 3+1i -> 3+i ・比較演算子・関係演算子 -3<-2<-1 // NG -> 0 -2==-2==-2 // NG -> 0 -3<-2&&-2<-1 -> 1 -2==-2&&-2==-2 -> 1 ・代入処理 a=b=1 -> [MyErr]Invalid ans isFound (b=1,a=b,a,b) -> (0,0,1,1) |
|
目次
Simple Calculator UI |
Simple Calculatorの操作panelについて記述する
panel上段について記述する ・draggable checked時、panelのdrag移動有効化 ・log出力欄に入力欄の演算結果のlogを表示 文字数制限5000字以内 ・入力欄に演算内容を入力 ・sw checked時、push/pop入力と直接入力を切替え可 ・0x checked時、16進数の0x-buttonとa-f-buttonを追加表示 Ver.2.146.37以降、ECMAScript6対応環境の場合、2進数の0b-buttonと8進数の0o-buttonを追加表示 ・ ・左側に0-9の数字と小数点.-buttonを表示 ・右側に四則演算の演算子記号-buttonを表示 panel右側について記述する ・C-buttonは入力欄&log出力欄の内容とglobal storageのClear実行を確定する Multi-thread実行の場合、演算を中断する ・BS-buttonは入力欄の選択位置の1字前を消去する ・ans-buttonはlog出力欄の演算結果を入力欄に確定する 演算結果が実数以外の場合、入力欄を消去して予約変数ansのtextを挿入 ・=-buttonは入力欄の内容で演算実行を確定する panel中段について記述する ・ 虚数単位i-buttonを追加表示 ・matrix checked時、行列演算を有効化 ・Ver.2.166.40以降、strict checked時、strict-modeを有効化 ・演算結果の小数表記と指数表記を選択可 小数表記: 0.1 指数表記: 1e-1 -> 0.1 panel下段について記述する ・history欄に最新を上にして演算履歴を表示 文字数制限5000字以内 ・history欄下のlinkから演算履歴の全文をtext保存可 入力欄のspell-check等でbrowser-busy状態の場合、download開始の待ち時間が生じる 再downloadのbrowser-blockあり(保存file更新の許可が必要) 一般的な電卓の操作性を再現する場合、all checkbox unchecked ・遅延しないSingle-threadの実数演算 ・応答時間=log表示待機時間50msec+演算量に応じた演算時間 各checkboxの詳細は外部option参照 |
|
目次
Graphing Calculator UI |
Graphing Calculatorの操作panelについて記述する
panel上段について記述する ・test caseを右側に配置 ・Ver.2.136.35以降、centering checked時、panelのcentering有効化 ・Ver.2.843.147以降、wheel checked時、mouse-wheelによるzooming有効化 ・draggable checked時、panelのdrag移動有効化 ・Ver.2.190.44以降、canvas上部でplot2d-Verを選択可 Ver.0:Ver.2.33.17以前の仕様(oldPlot2d=true) Ver.1:Ver.2.33.17~2.190.44の仕様 Ver.2:Ver.2.190.44~の仕様 ・canvas上部のlinkから描画結果のpng||svg||csvを保存可 ・pngは描画終了||中断後に保存可(逐次layer合成しない) ・右click||long-tapによるpng保存不可(最前面固定layerは範囲選択領域の描画用) ・svg||csvはMulti-thread実行の場合、逐次保存可 ・png||svg出力共通でcanvas座標小数点以下floorの出力桁数0~9桁を選択可 ・canvasにplot2dの演算&描画結果を表示 ・mouse||touchによる範囲選択で拡大表示 ・single click||one tapで ・Ver.2.117.33以降、pointing deviceに対応 ・Ver.2.843.147以降、mouse-wheelの垂直方向のscroll量deltaYによるzoomingに対応(基数2) ・Ver.2.822.135以降、last入力欄は最終legendからの表示legend数を入力可(0の場合、全表示) ・Ver.2.601.94以降、plot範囲の小数点以下のround-off桁数を選択可(指数表記選択より優先) Ver.2.666.98以降、y||xの各軸を設定可 ・Ver.2.780.123以降、y(t)||x(t)入力欄の行数を選択可 ・Ver.2.401.86以降、p-checkboxは全labelの Ver.2.746.111以降、表示機能を反転(checkedで全表示) gradation/string-path同様に、全体表示の保証を優先 ・log出力欄にplot2dの演算&描画結果のlogを表示 Ver.2.387.86~2.391.86以降、演算中のlog表示を変更:finished ⇒ finished... ・plot-buttonは演算&描画実行を確定する Ver.2.360.86以降、要素位置を微調整 Ver.2.759.115以降、自動描画refreshの頻度:最大10回 ⇒ 最短1秒間隔 ・stop-buttonは演算&描画実行を中断する・軸scaleを初期化する Ver.2.360.86以降、要素位置を微調整 ・l-checkboxはlegend表示を選択 ・t入力欄に媒介変数の区間[t0,t1]を入力 ・Ver.2.34.18以降、t-checkboxはlinear||logarithmicの軸scaleを選択 Ver.2.50.25以降、checked時、t0||t1の入力規則を緩和(実部||虚部のみに対応) Ver.2.50.25以降、副次的にcomplex unchecked時、logarithmic-scale選択不能の不具合を解消 Ver.2.444.90以降、分割点の丸め方を最適化(Machine epsilon程度の相違あり) ・媒介変数tの区間分割数Nを Ver.2.321.77以降、上限値:1000 ⇒ 1024 Ver.2.392.86以降、下限値:1 ⇒ 0(t1=t0) ・x(t)入力欄に横軸xの演算内容をsemi-colon;区切りで入力 Ver.2.352.86以降、x(t)||y(t)||z入力欄の形式を変更(<input> ⇒ <textarea></textarea>) ・tは媒介変数で上書き可能なlocal変数 Ver.2.85.32以降、N/t0/t1をlocal変数に追加 ・直下のx-checkboxはx-label/x-values表示を選択 Ver.2.53.26以降、unchecked時、z入力欄のx-label特定項目が残存する不具合を修正 ・log-checkboxは対数表示を選択 ・i-checkboxは虚数表示を選択 ・x(t)のplot範囲のaxis最小値~最大値を入力可 ・y(t)入力欄に縦軸yの演算内容をsemi-colon;区切りで入力 Ver.2.352.86以降、x(t)||y(t)||z入力欄の形式を変更(<input> ⇒ <textarea></textarea>) ・tは媒介変数で上書き可能なlocal変数 ・直下のy-checkboxはy-label/y-values表示を選択 Ver.2.53.26以降、unchecked時、z入力欄のy-label特定項目が残存する不具合を修正 ・log-checkboxは対数表示を選択(通常の対数scaleとは異なり、常用対数の数値に変換して表示) Ver.2.750.113~2.773.119以降、checked時、軸labelの追加表示に対応(表示内容を明示):log10(axis-label) ・i-checkboxは虚数表示を選択(対数表示より優先) Ver.2.750.113~2.773.119以降、checked時、軸labelの追加表示に対応(表示内容を明示):imag(axis-label) ・y(t)のplot範囲のaxis最小値~最大値を入力可 ・Ver.2.36.18以降、z-checkboxはz入力欄の表示を選択 Ver.2.746.111以降、checked時、z入力欄を有効化 最終frameまでの特定項目を除く描画待ち時間||描画負荷を省略する場合、unchecked Ver.2.37.18以降、gridのscalingに対応 ・canvas範囲選択でx(t)||yt(t)のplot範囲の各axis最小値~最大値をlinear-scaleで自動更新 複数の方程式||関数式の交点等を求める際に有効 Ver.2.39.18以降、x0.1/x0.5/x1/x2/x10-buttonsは指定のzoom倍率でscalingを確定する Ver.2.360.86以降、canvas直下に要素を移動 Ver.2.374.86以降、x1-buttonのsizeを調整 ・zoom倍率はlinear-scale Ver.2.842.147以降、logarithmic-scaleに対応 ・x1-buttonはscalingをresetする ・rel.-checkboxは原点に対してzoom中心位置を相対的に移動するrelative zoomingを選択 Ver.2.852.157以降、unchecked時のscalingの丸め処理を調整 Ver.2.39.18以降、gridのsnappingに対応 ・long-tap||clickの300msec後にsnapping開始 ・canvas範囲選択でscaling ・その場releaseでcentering ・Ver.2.40.19以降、x||y方向の移動なしで選択cancel ・snap-checkboxはgrid snappingを選択 Ver.2.360.86以降、canvas直下に要素を移動 Ver.2.40.19以降、click||tap連打による描画の排他処理を修正 ・連打による副作用をonmouseup-handlerでlock判定して回避 ・checkbox等UI操作も同様にlock判定されるため、弾かれた場合、unlock後に再描画が必要 ・lock判定のreturn false直後にisLocked=true ・Ver.2.40.20以降、error終了時、isLocked=falseでdeadlockを回避 ・以上より、副次的に2本指での範囲選択に対応(touch deviceのみ) Ver.2.40.20以降、plot2d isNaN||isInfのerror終了時、描画resetから描画lockに変更 Ver.2.105.33以降、v入力仕様を追加 Ver.2.437.90以降、path出力欄を追加 ・ ・最終legendのみ ・path: ・小数点以下floor有効 panel中段について記述する ・C-input-buttonは入力欄のtextを消去する ・list-vars-buttonはglobal変数の変数名listをlog出力欄に表示する ・list-eqns-buttonはglobal式変数の変数名listをlog出力欄に表示する Ver.2.50.25以降、plot2d(xt,yt)のtextを挿入する ・Ver.2.140.36以降、plot2d()-buttonは任意の変数名symbolを入力してplot2d(xt,yt)を実行する ・Ver.2.175.42以降、plot2d{}-buttonは任意の変数名symbolを入力してplot2d{xt,yt}を実行する ・<<-buttonは入力欄の選択位置を最初に移動する ・<-buttonは入力欄の選択位置を1字前に移動する ・>-buttonは入力欄の選択位置を1字後に移動する ・>>-buttonは入力欄の選択位置を最後に移動する ・=-buttonは入力欄の内容で演算実行を確定する ・C-buttonは入力欄&log出力欄の内容とglobal storageのClear実行を確定する Multi-thread実行の場合、無条件に演算を中断する ・Ver.2.140.36以降、cancel-buttonはMulti-thread実行中の演算を中断する ・BS-buttonは入力欄の選択位置の1字前を消去する ・DEL-buttonは入力欄の選択位置の1字後を消去する ・i-buttonは入力欄の選択位置に虚数単位iのtextを挿入する ・()-buttonは入力欄の選択位置に丸括弧()のtextを挿入する ・{}-buttonは入力欄の選択位置に波括弧{}のtextを挿入する ・ans-buttonは入力欄の選択位置に予約変数ansのtextを挿入する Multi-thread実行の場合、plot-buttonと=-buttonは並列に実行可 ・shared storage checked時、global storageを共有 ・plot-buttonによる演算はglobal storage readonly panel下段はSimple Calculator UI参照 |
|
目次
color空間 |
color空間について記述する
RGB-color空間 ・Red(赤) ・Green(緑) ・Blue(青) 主な用途は光の三原色による加法混合のdisplay RGBA-color空間 ・Alpha(不透明度) 主な用途はcomputer graphics(HTML5描画canvas標準の場合、sRGBA-color空間) HSV-color空間 ・Hue(色相) ・Saturation(彩度∝RGB最大値-RGB最小値) ・Value(明度=RGB最大値) 主な用途は直感的な操作のcolor-picker ・SaturationをValueで正規化する場合、円柱model(色相環内側のpicker領域がsquare) ・Saturationを正規化しない場合、円錐model(色相環内側のpicker領域がtriangle) HSL-color空間 ・Lightness(輝度=(RGB最小値+RGB最大値)/2) 主な用途は直感的な操作のcolor-picker XYZ-color空間(CIE 1931表色系) ・XYZ(Yを輝度とする3刺激値) 主な用途はgamma補正前の仕様違いcolor空間の相互変換における包括的な中継 ・CIE RGB->CIE XYZ線形変換 {$X,$Y,$Z}=scalars(3,1/0.17697)*( 0.49000,0.31000,0.20000: 0.17697,0.81240,0.010630: 0.0000,0.010000,0.99000 )*{R,G,B} ・CIE XYZ->CIE RGB線形逆変換 {$R,$G,$B}=( 0.4184657124218945,-0.15866078480379903,-0.08283492761809548: -0.09116896390902272,0.2524314421394651,0.015707521769557607: 0.0009208986253436638,-0.0025498125468632836,0.1785989139215196 )*{X,Y,Z} ※有効桁数5桁 |
|
目次
color 入力仕様 |
color入力仕様について記述する
HTML5/CSS3準拠のcolor入力方法を次に示す color名||HEX表記RGB||RGBA||rgb(r,g,b=0~255)||rgba(r,g,b,不透明度a=0~1) 透明黒色の初期状態を定義する #0000||#00000000||rgba(0,0,0,0) 最背面固定layerに描画する千鳥格子の配色を定義する※格子size(8px)x(8px) rgba(211,211,211,1)||lightgray rgba(240,240,240,1) 範囲選択領域の配色を定義する rgb(7,135,200) rgba(255,128,128,0.75) Ver.2.846.153以降、fillあり color入力の一例を示す ・white white||#fff||#ffff||#ffffff||#ffffffff||rgb(255,255,255)||rgba(255,255,255,1) ・black black||#000||#000f||#000000||#000000ff||rgb(0,0,0)||rgba(0,0,0,1) ・gray gray||#808080||#808080ff ・red red||#f00||#f00f||#ff0000||#ff0000ff||rgb(255,0,0)||rgba(255,0,0,1) ・blueの不透明度a=0.333333333333333 #00f5||#0000ff55||rgba(0,0,255,0.333333333333333) Ver.2.134.35以降、legend番号Nlegend=j+1のmarker-colorsのRGB既定値を示す(参考) 留意事項を列挙する ・未定義の場合、透明黒色 ・rgba()入力のRGBA指定値≒picker値で数%以内の誤差が存在する可能性あり(詳細は未検証) |
|
目次
colors 入力仕様 |
colors入力仕様について記述する
・Ver.2.36.18以降、gradation-colorsに適用 ・Ver.2.744.110以降、marker-colorsに適用 ・Ver.2.846.153以降、mrcolorsに適用 color-datasetの一例:7色rainbow ・marker-colorsのrainbow選択時、colorのpn=[1/7,7/7]のRGB値をround出力 rgb(255,0,219):rgb(73,0,255):rgb(0,146,255):rgb(0,255,146):rgb(73,255,0):rgb(255,219,0):rgb(255,0,0) ・Newton説(音階analogyによる) violet:indigo:blue:green:yellow:orange:red #ee82ee:#4b0082:#0000ff:#00ff00:#ffff00:#ffa500:#ff0000 #ee82eecc:#4b0082cc:#0000ffcc:#00ff00cc:#ffff00cc:#ffa500cc:#ff0000cc ・Ver.2.42.20以降、modern風 violet:blue:cyan:green:yellow:orange:red #ee82ee:#0000ff:#00ffff:#00ff00:#ffff00:#ffa500:#ff0000 #ee82eecc:#0000ffcc:#00ffffcc:#00ff00cc:#ffff00cc:#ffa500cc:#ff0000cc ・Ver.2.44.22以降、fade-in/out境界条件を追加 #ee82ee00:#ee82eecc:#0000ffcc:#00ffffcc:#00ff00cc:#ffff00cc:#ffa500cc:#ff0000cc:#ff000000 ・6色の場合、短波長側のindigo||cyanを消去 |
|
目次
z入力仕様 |
z入力欄の入力仕様について記述する
Ver.2.352.86以降、x(t)||y(t)||z入力欄の形式を変更(<input> ⇒ <textarea></textarea>) ・Ver.2.354.86以降、内容変更時、自動re-plotの機能を継承 legend-datasetをsemi-colon;区切りで入力 ・空欄で既定の描画 ・datasetは設定値をcolon:区切りで入力 markerType:markerColor:markerSize:markerLineWidth:plotLineWidth:fillPath: str:strFontSize 以降、その他の特定項目を抽出順に列挙する Ver.2.66.27以降、bgcolorを追加 bgcolor||BGCOLOR{color} ・任意位置に挿入可 ・background-layerにcolor指定値を適用 Ver.2.66.27以降、gdcolorを追加 gdcolor||GDCOLOR{color} ・任意位置に挿入可 ・grid-layerにcolor指定値を適用 Ver.2.846.153以降、mrcolorsを追加 mrcolors||MRCOLORS{colors} ・任意位置に挿入可 ・marker-colorsにcolors指定値を適用 ・colorsはcolor-datasetをcolon:区切りで入力 Ver.2.848.155以降、compositesを入力 composites||COMPOSITES{composite0,composite1} ・任意位置に挿入可 ・compositeをcomma,区切りで入力 ・canvas-globalCompositeOperationLayerにcomposite0を適用 ・canvas-globalCompositeOperationにcomposite1を適用 Ver.2.92.32以降、plotconfigを追加 plotconfig||PLOTCONFIG{args} ・任意位置に挿入可 ・argsは設定値をcomma,区切りで入力(0||省略時、plot-configの設定値) grid-line-width,font-size,grid-x-Ni,grid-y-Nj,kx-adj,legend-kx,legend-ky Ver.2.34.18以降、graph-titleを追加 title||TITLE{graph-title} ・任意位置に挿入可 ・graph-titleはcanvas上部に表示するtitleの任意文字列でgrid-layerに描画 Ver.2.37.18以降、x-labelを追加 xlabel||XLABEL{x-label} ・任意位置に挿入可 ・x-labelはx軸余白に表示するlabelの任意文字列でgrid-layerに描画 Ver.2.37.18以降、y-labelを追加 ylabel||YLABEL{y-label} ・任意位置に挿入可 ・y-labelはy軸余白に表示するlabelの任意文字列でgrid-layerに描画 Ver.2.67.27以降、originを追加 origin||ORIGIN{args} ・任意位置に挿入可 ・originはorigin-labelと原点を通るorigin-lineでgrid-layerに描画 ・argsは設定値をcomma,区切りで入力(省略時、legend-datasetの設定値) lineWidth,color,labelSize ↑設定機能(UI設定値||既定値を上書き) ↓描画機能 Ver.2.34.18以降、string-pathを追加 string||STRING{config[]string-path} ・各legend-datasetの任意位置に挿入可 ・string-pathはplot-lines上のpathに表示する任意文字列でplot-layerに描画 ・config[]内datasetは設定値をcolon:区切りで入力(省略時、legend-datasetの設定値) fontFamily:fontSize:isBold:isItalic:isReverse: fillStyle:strokeStyle:fillStr:spacingX:spacingY: shadowOffsetX:shadowOffsetY:shadowBlur:deg0 Ver.2.35.18以降、graph-title/legend-string/string-pathのwhite space enabled Ver.2.36.18以降、gradationを追加 gradation||GRADATION{config[]colors} ・各legend-datasetの任意位置に挿入可 ・gradationはplot-layerに描画 ・colorsはcolor-datasetをcolon:区切りで入力(省略時、legend-datasetのmarkerColor) ・config[]内datasetは設定値をcolon:区切りで入力(省略不可) originX:originY:offsetR:orderR:NrandR:NrandT:isMin:isRound:Nrender:Ncycle Ver.2.52.25以降、transformを追加 transform||TRANSFORM{args} ・任意位置に挿入可 ・transformはlayer合成時のpost処理(Ver.2.56.26以降、svg出力に対応) ・argsはcanvas座標変換の引数をcomma,区切りで入力 Ver.2.45.23以降、blurを追加 blur||BLUR{asym[]config[]strengths} ・任意位置に挿入可 ・blurはfiltering直前のpost最終処理(svg出力は無効) ・strengthsはfilter(2n-1)x(2n-1)sizeのn=0~20の数値をcolon:区切りで入力(省略時、0:10) ・config[]内datasetは設定値をcolon:区切りで入力(省略不可) originX:originY:offsetR:orderR:NrandR:NrandT:isMin:isRound:Nrender:Ncycle: isCyclic:isSquare:Nlegend(Ver.2.55.26以降、項目名を変更) ・Ver.2.57.26以降、asym[]内datasetは設定値をcomma,区切りで入力(省略時、0,0,1,0) x,y,k,Nrad Ver.2.44.22以降、filterを追加 filter||FILTER{filters} ・任意位置に挿入可 ・filterはlayer合成後のpost最終処理(svg出力は無効) ・filtersはmask[]area[]filterを適用順にcolon:区切りで入力 ・Ver.2.52.25以降、area[]内datasetは設定値をcomma,区切りで入力(省略時、全体に適用) ・Ver.2.63.27以降、mask[]内datasetは設定値をcomma,区切りで入力(省略時、全体に適用) Ver.2.68.27以降、tileを追加 tile||TILE{args} ・任意位置に挿入可 ・tileはfiltering直後のpost最終処理(svg出力は無効) ・argsはtile領域を指定する条件をcomma,区切りで入力 Ver.2.63.27以降、cutを追加 cut||CUT{args} ・任意位置に挿入可 ・cutはfiltering直後のpost最終処理(svg出力はlayer合成) ・argsはcut領域を指定する条件をcomma,区切りで入力 |
|
目次
legend -dataset |
legend-datasetについて記述する
・Ver.2.744.111以降、sizeのlimiterを追加(負の場合、予期せぬerror終了を修正) z入力欄にlegend-datasetをsemi-colon;区切りで入力 ・legendはplot-layerに描画 Ver.2.851.157以降、左上のbox部分のみ、source-over固定(後方互換性のため、markerを除く) ・datasetは設定値をcolon:区切りで入力 markerType:markerColor:markerSize:markerLineWidth:plotLineWidth:fillPath: str:strFontSize ・markerTypeはnone||circle||triangle||triangle2||square||diamond||cross Ver.2.859.159以降、markerTypeとstrが未定義の場合、legend-stringを代替 ・markerColorはmarker-colorの入力値 ・markerSizeはmarkerTypeの目安size ・markerLineWidthはmarker-line-widthのpx数値 ・plotLineWidthはplot-line-widthのpx数値 ・fillPathは0以外を指定でplot線を閉じてfill ・strはlegend-string ・strFontSizeはlegend-stringのfont-sizeのpx数値 ・字句解析の都合上、legend-stringのsemi-colon; disabled |
|
目次
bgcolor 特定項目仕様 |
bgcolor特定項目仕様について記述する
Ver.2.66.27以降、z入力欄にbgcolorを入力 bgcolor||BGCOLOR{color} ・任意位置に挿入可 ・background-layerにcolor指定値を適用 |
|
目次
gdcolor 特定項目仕様 |
gdcolor特定項目仕様について記述する
Ver.2.66.27以降、z入力欄にgdcolorを入力 gdcolor||GDCOLOR{color} ・任意位置に挿入可 ・grid-layerにcolor指定値を適用 |
|
目次
mrcolors 特定項目仕様 |
mrcolors特定項目仕様について記述する
Ver.2.846.153以降、z入力欄にmrcolorsを入力 mrcolors||MRCOLORS{colors} ・任意位置に挿入可 ・marker-colorsにcolors指定値を適用 ・colorsはcolor-datasetをcolon:区切りで入力 |
|
目次
composites 特定項目仕様 |
composites特定項目仕様について記述する
Ver.2.848.155以降、z入力欄にcompositesを入力 composites||COMPOSITES{composite0,composite1} ・任意位置に挿入可 ・compositeをcomma,区切りで入力 ・canvas-globalCompositeOperationLayerにcomposite0を適用 ・canvas-globalCompositeOperationにcomposite1を適用 |
|
目次
plotconfig 特定項目仕様 |
plotconfig特定項目仕様について記述する
Ver.2.92.32以降、z入力欄にplotconfigを入力 plotconfig||PLOTCONFIG{args} ・任意位置に挿入可 ・argsは設定値をcomma,区切りで入力(0||省略時、plot-configの設定値) grid-line-width,font-size,grid-x-Ni,grid-y-Nj,kx-adj,legend-kx,legend-ky ・grid-x-Ni=0~2560 ・grid-y-Nj=0~2560 |
|
目次
graph-title 特定項目仕様 |
graph-title特定項目仕様について記述する
Ver.2.34.18以降、z入力欄にgraph-titleを入力 title||TITLE{graph-title} ・任意位置に挿入可 ・graph-titleはcanvas上部に表示するtitleの任意文字列でgrid-layerに描画 |
|
目次
axis-labels 特定項目仕様 |
axis-labels特定項目仕様について記述する
Ver.2.37.18以降、z入力欄にx-labelを入力 xlabel||XLABEL{x-label} ・任意位置に挿入可 ・x-labelはx軸余白に表示するlabelの任意文字列でgrid-layerに描画 ・省略時、軸labelの表示:x(t) Ver.2.37.18以降、z入力欄にy-labelを入力 ylabel||YLABEL{y-label} ・任意位置に挿入可 ・y-labelはy軸余白に表示するlabelの任意文字列でgrid-layerに描画 ・省略時、軸labelの表示:y(t) 留意事項を列挙する ・Ver.2.750.113~2.773.119以降、軸labelの追加表示を削除する場合、plot内容の要変更 log10(imag(label)) ⇒ labelの場合、z ⇒ log10(imag(z)) |
|
目次
origin 特定項目仕様 |
origin特定項目仕様について記述する
Ver.2.67.27以降、z入力欄にoriginを入力 origin||ORIGIN{args} ・任意位置に挿入可 ・originはorigin-labelと原点を通るorigin-lineでgrid-layerに描画 ・argsは設定値をcomma,区切りで入力(省略時、legend-datasetの設定値) lineWidth,color,labelSize 留意事項を列挙する ・comma,区切りの場合、rgba()入力のcolor指定不可 |
|
目次
string-path 特定項目仕様 |
string-path特定項目仕様について記述する
Ver.2.34.18以降、z入力欄にstring-pathを入力 string||STRING{config[]string-path} ・各legend-datasetの任意位置に挿入可 ・string-pathはplot-lines上のpathに表示する任意文字列でplot-layerに描画 ・config[]内datasetは設定値をcolon:区切りで入力(省略時、legend-datasetの設定値) fontFamily:fontSize:isBold:isItalic:isReverse: fillStyle:strokeStyle:fillStr:spacingX:spacingY: shadowOffsetX:shadowOffsetY:shadowBlur:deg0 Ver.2.37.18以降、各設定値のlimiterを追加 ・fontFamilyはfont-family名(Ver.2.35.18以降、white space付family名に対応) ・fontSize=0~32767はstring-pathのfont-sizeのpx数値 ・isBold=0||white space以外でbold typeを使用 ・isItalic=0||white space以外でitalic typeを使用 ・isReverse=0||white spaceで始点から順送り・それ以外は終点から順送り ・fillStyleはfill-style ・strokeStyleはstroke-style ・fillStr=falseでstrokeのみ・fillStr=trueでfillのみ・それ以外はstroke&fill ・spacingX=-32768~32767は文字送り空白部分のpx数値 ・spacingY=-32768~32767は高さ方向空白部分のpx数値 ・shadowBlur>0でshadow有効(png/svg出力の互換性なし) ・shadowColorはfillStr=falseでstrokeStyle・fillStr=trueでfillStyle ・それ以外はfillStr=0~255を比例係数とするstrokeStyleとfillStyleのRGBA値の線形補間 ・R値の一例を次に示す shadowColor.r = strokeStyle.r+(fillStyle.r-strokeStyle.r)*Math.min(1, Math.abs(fillStr)/255) ・shadowOffsetX=-32768~32767はshadowのx方向offsetのpx数値 ・shadowOffsetY=-32768~32767はshadowのy方向offsetのpx数値 ・shadowBlur=-32768~32767はshadowの偏差 ・character毎にsvg出力の度数degをpng出力の弧度数radに変換して互換性を確保 ・以上の座標変換はcharacterのbottom-left基準 Ver.2.37.18以降、path上の回転角のみ、svg-<textPath>準拠のbottom基準に変更 ・Ver.2.37.18以降、config[]内datasetに設定項目deg0を追加 ・deg0=0~360はcharacterのbottom-left基準の回転角の度数deg deg0=0||省略時・spacingX/Y=0||省略時、path上の回転角を使用 ・字句解析の都合上、string-pathのsemi-colon; disabled ・仕様上、string-pathの4Bytes character disabled ・svg出力のみ、4Bytes characterを含む特殊文字等、直接file編集可(group化済み) Ver.2.37.18以降、spacingX/Y=0||省略時、<textPath>によるsvg出力に対応 ・回転角を含む座標変換のalgorithmが異なるため、png出力と若干の互換性を失う ・svg出力は縮小表示でtextPathが非表示になるが、png出力は非表示にならない ・string-pathにwhite spacesを含む場合、spellの扱いが異なる(1字に変換すれば統一可) ・<textPath>以外への流用等、利便性に配慮し、既定で<path>を出力する 留意事項を列挙する ・string部分のみを描画する場合、canvas-globalCompositeOperation=source-in/out||destination-in/atopを選択(label作成用) |
|
目次
gradation 特定項目仕様 |
gradation特定項目仕様と付随する留意事項について記述する
Ver.2.36.18以降、指向性のないGaussぼかしでは再現困難な機能としてgradationを追加する ・Ver.2.40.18以降、legend間のgradation合成に対応 ・Ver.2.60.26以降、circle-mode@Ncycle=0を追加 z入力欄にgradationを入力 gradation||GRADATION{config[]colors} ・各legend-datasetの任意位置に挿入可 ・gradationはplot-layerに描画 ・gradation起点からplot-lineまでの半径方向に生成 ・colorsはcolor-datasetをcolon:区切りで入力(省略時、legend-datasetのmarkerColor) ・config[]内datasetは設定値をcolon:区切りで入力(省略不可) originX:originY:offsetR:orderR:NrandR:NrandT:isMin:isRound:Nrender:Ncycle ・svg出力はorderR:NrandR:NrandT:isMin:isRound:Nrender disabled ・originXはplot座標系x方向linear-scaleのgradation起点 ・originYはplot座標系y方向linear-scaleのgradation起点 ・offsetR=0~1はgradation代表長さのoffset係数 offsetR=0の場合、最外周を除く内周にgradationの周期境界条件を課す ・orderR=0~10は半径方向の補間次数 orderR=0の場合、svg出力相当のuniform orderR=1の場合、既定の線形補間 ・NrandR=0~255はgradation代表長さの乱数 ・NrandT=0~255はgradation分布の乱数 ・isMin=false||true||<0(auto)はgradation代表長さの一意な決め方を指定する falseの場合、gradation起点から各周plot点までの最大値を保持 trueの場合、gradation起点から各周plot点までの最小値を保持 負の場合、成行きで保持 ・isRound=false||trueはplot点の存在しない領域の補間方法を選択する falseの場合、plot座標系で線形補間(plot間vectorを等分割して回転角に変換する誤差あり) trueの場合、gradation起点からplot点までの長さ空間で線形補間(false同様の誤差あり) ・Nrender=1~32767は周方向のrendering分割数(数値以外を指定時、媒介変数tの区間分割数N) ・Ncycle=0~127は半径方向のrendering周期数 Ver.2.60.26以降、circle-mode@Ncycle=0を追加 ・canvas座標でgradation起点を中心にplot-lineの周方向に生成(canvas-sizeに依存) ・config[]内datasetの変化点を示す originX:originY:offsetR:orderR:NrandR:NrandT:isMin:isRound:Nrender:Ncycle=0 ・isRound disabled ・offsetR=0~1は1周のoffset係数 offsetR=0の場合、gradationの周期境界条件を課す ・NrandR=0~255はgradation間隔の乱数 ・isMin=false||trueはrenderingの重複を判定する falseの場合、成行きでrendering trueの場合、重複判定でrenderingをskip algorithmが異なるため、png/svg出力の互換性なし svg出力の特徴を列挙する ・Nrender無効 ・plot点に比例係数を演算してgradationを作るため、意図に近い結果が得られる ・legend間のgradation合成可(source-over) ・乱数適用不可 ・circle-mode@Ncycle=0の場合、周方向の分割数=(NrandT||10)*colors.length ・gradation精度を上げる場合、colorsを細かく刻んで指定する png出力の特徴を列挙する ・rendering方式でRGBA値を補間するため、gradation精度が高い ・isMin設定値によってcyclic star||spiral等、意図した結果が得られるとは限らない ・isRound設定項目の変換誤差を許容するため、 svg出力同等||完全に意図通りの結果は得られない(Ver.2.44.23追記) ・Ver.2.40.18以降、legend間のgradation合成に対応 ・putImageData()同期出力のため、canvas-globalCompositeOperation無効(source-over) ・乱数適用可 ・Nrender=1で真円のgradationが比較的簡単に得られる 形状再現精度||gradation精度に関係する設定項目を列挙する ・媒介変数tの区間分割数N ・周方向のrendering分割数Nrender ・png||svg出力桁数 ・circle-mode@Ncycle=0の場合 ・plot範囲の各axis最小値~最大値 ・canvas-size@p-checkbox unchecked 留意事項を列挙する ・上記精度を上げ過ぎた場合、svg出力のfile sizeやpost処理の負荷が増大する ・乱数設定時、flickering防止のため、 Ver.2.759.115以降、自動描画refreshの頻度:最大10回 ⇒ 最短1秒間隔 ・drawImage()非同期出力のため、最終frameにlegend順を保証してgradationを合成する |
|
目次
transform 特定項目仕様 |
transform特定項目仕様と付随する留意事項について記述する
Ver.2.52.25以降、layer合成時の座標変換機能を追加する ・Ver.2.53.25以降、せん断変換の結果から座標変換行列の一部(b:c)の位置関係を交換して訂正 ・Ver.2.56.26以降、設定項目withBackgroundを追加 ・Ver.2.56.26以降、svg出力に対応 z入力欄にtransformを入力 transform||TRANSFORM{args} ・任意位置に挿入可 ・transformはlayer合成時のpost処理(Ver.2.56.26以降、svg出力に対応) ・argsはcanvas座標変換ctx.setTransform(a,b,c,d,e,f)の引数をcomma,区切りで入力 transform{a,b,c,d,e,f,withBackground||0} ・各引数の定義 2次元Euclid実空間の回転行列(a,c:b,d) px数値の並進vector{e,f} ・withBackground=0||1(background-layerにtransformを適用する場合、1) ・座標変換行列の定義 transform3x3=( a,c,e: b,d,f: 0,0,1 ) transpose(transform3x3) -> ( a,b,0: c,d,0: e,f,1 ) ・列vectorの場合 {x_after,y_after,1}=transform3x3*{x_before,y_before,1} ・行vectorの場合 (x_after,y_after,1)=(x_before,y_before,1)*transpose(transform3x3) ・同義 x_after=x_before*a+y_before*c+1*e y_after=x_before*b+y_before*d+1*f ・逆変換 determinant=(a*d-b*c) inverse(transform3x3) -> ( (1/determinant)*(d,-c,c*f-e*d): (1/determinant)*(-b,a,e*b-a*f): (1/determinant)*(0,0,a*d-c*b) ) x_before=(1/determinant)*(x_after*d+y_after*(-c)+1*(c*f-e*d)) y_before=(1/determinant)*(x_after*(-b)+y_after*a+1*(e*b-a*f)) ・演算に使用する場合、Napier数eと区別が必要 test caseを列挙する ・基準{x_before,y_before,1}={1,1,1} {1,0,0,1,0,0} args={1,0,0,1,0,0}; transform3x3=(args[0],args[2],args[4]:args[1],args[3],args[5]:0,0,1); {$x_before,$y_before,1}={1,1,1}; {$x_after,$y_after,1}=transform3x3*{x_before,y_before,1}; {x_after,y_after,1} -> (1:1:1) ・x方向2倍(a,d)=(2,1) {2,0,0,1,0,0} {x_after,y_after,1} -> (2:1:1) ・y方向2倍(a,d)=(1,2) {1,0,0,2,0,0} {x_after,y_after,1} -> (1:2:1) ・並進(e,f)=(-100,100) {1,0,0,1,-100,100} {x_after,y_after,1} -> (-99:101:1) ・x方向反転並進(a,e)=(-1,100) {-1,0,0,1,100,0} {x_after,y_after,1} -> (99:1:1) ・y方向反転並進(d,f)=(-1,100) {1,0,0,-1,0,100} {x_after,y_after,1} -> (1:99:1) ・x/y方向反転並進(a,d,e,f)=(-1,-1,100,100) {-1,0,0,-1,100,100} {x_after,y_after,1} -> (99:99:1) ・回転(a,b)=(d,-c) ・回転角=pi/4 rotz_LHS(psi)=<{rt=real(psi),=<(cos(rt),sin(rt),:-sin(rt),cos(rt),:,,1)}=>; Rz=rotz_LHS(pi/4); Rz[0][0],Rz[0][1],Rz[1][0],Rz[1][1] -> 0.7071067811865476,0.7071067811865475,-0.7071067811865475,0.7071067811865476 {0.7071067811865476,0.7071067811865475,-0.7071067811865475,0.7071067811865476,0,0} {x_after,y_after,1} -> (1.1102230246251565e-16:1.414213562373095:1) ・(a,b)=(0.5,0.2) {0.5,0.2,-0.2,0.5,0,0} {x_after,y_after,1} -> (0.3:0.7:1) ・x方向せん断変換(b,c)=(0,0.5) {1,0,0.5,1,0,0} {x_after,y_after,1} -> (1.5:1:1) ・y方向せん断変換(b,c)=(0.5,0) {1,0.5,0,1,0,0} {x_after,y_after,1} -> (1:1.5:1) ・視線変更 {1,0.1,-0.5,0.5,50,50} {x_after,y_after,1} -> (50.5:50.6:1) 留意事項を列挙する ・layer合成後のblurring||filteringはputImageData()同期出力のため、transform無効 ・layer合成後のblurring||filteringにtransformを適用する場合、post-transformer参照 |
|
目次
blur 特定項目仕様 |
blur特定項目仕様と付随する留意事項について記述する
Ver.2.45.23以降、averageぼかしを応用して指向性のblurを追加する ・Ver.2.45.24以降、strength=0で正常に機能しない致命的な不具合を修正 ・Ver.2.55.26以降、一部の設定項目名をisSquareに変更 ・Ver.2.57.26以降、非対称averageぼかしに対応(asym[]の設定項目を追加) ・Ver.2.60.26以降、circle-mode@Ncycle=0を追加 z入力欄にblurを入力 blur||BLUR{asym[]config[]strengths} ・任意位置に挿入可 ・blurはfiltering直前のpost最終処理(svg出力は無効) ・strengthsはfilter(2n-1)x(2n-1)sizeのn=0~20の数値をcolon:区切りで入力(省略時、0:10) ・config[]内datasetは設定値をcolon:区切りで入力(省略不可) originX:originY:offsetR:orderR:NrandR:NrandT:isMin:isRound:Nrender:Ncycle: isCyclic:isSquare:Nlegend(Ver.2.55.26以降、項目名を変更) ・上段はgradation参照 ・Ver.2.57.26以降、非対称averageぼかしの場合、下流側でNrender=1~2560に上限値を圧縮 averageぼかしの場合、memory size<20MB 非対称averageぼかしの場合、memory size<200MB ・isCyclic=false||trueは1周期外(2周期目以降)のblur条件を選択する falseの場合、strengthsの最終値で固定してblurを適用 trueの場合、周期的にblurを適用 ・isSquare=false||trueは適用するfilterの種類を選択する falseの場合、average_circle trueの場合、average_square ・Nlegend=1~lastはblurを適用するplot-lineのlegend番号 範囲外の数値||数値以外を指定した場合、最終legendを選択 ・Ver.2.57.26以降、asym[]内datasetは設定値をcomma,区切りで入力(省略時、0,0,1,0) asym[x||0,y||0,k||0,Nrad||0] ・各設定値の詳細は非対称averageぼかし参照 ・Nradは回転行列の弧度数rad=pi/Nradに換算するpiの分割数(Nrad=0の場合、rad=0) ・radはplot-lineの接線方向(1次近似)を基準とする独立変数 test caseを列挙する ・strength分布に乱数を適用(glass morphism効果を模擬) config[0:0:0:1:0:50:false:false:2560:4:true:false:last] ・glass morphism効果を強化して密に適用 config[0:0:0:1:0:200:false:false:2560:4:true:false:last]0:10:0:10:0:10:0:10:0:10:0:10 config[0:0:0:1:0:200:false:false:2560:4:true:false:last]10:0:10:0:10:0:10:0:10:0:10:0 Ver.2.60.26以降、circle-mode@Ncycle=0を追加 ・Nlegend=1のplot-line上でstrength=0の周期境界条件を適用 config[0:0:0:1:0:0:false:false:2560:0:true:false:1]0:8 config[0:0:0:1:0:0:false:false:2560:0:true:false:1]0:8:8 ・Nlegend=1のplot-line上でstrength=0の非周期境界条件を適用 config[0:0:0:1:0:0:false:false:2560:0:false:false:1]0:8:0 config[0:0:0:1:0:0:false:false:2560:0:false:false:1]0:8:8:0 ・Nlegend=1のplot-line上でstrength=8の周期境界条件を適用 config[0:0:0:1:0:0:false:false:2560:0:true:false:1]8:0 config[0:0:0:1:0:0:false:false:2560:0:true:false:1]8:0:0 ・Nlegend=1のplot-line上でstrength=8の非周期境界条件を適用 config[0:0:0:1:0:0:false:false:2560:0:false:false:1]8:0:8 config[0:0:0:1:0:0:false:false:2560:0:false:false:1]8:0:0:8 ・非対称averageぼかしを適用 asym[0,0,3,0]config[0:0:0:1:0:0:false:false:2560:0:true:false:1]0:8:8 形状再現精度||blur精度に関係する設定項目を列挙する ・媒介変数tの区間分割数N ・周方向のrendering分割数Nrender 留意事項を列挙する ・svg出力は無効 ・putImageData()同期出力のため、canvas-globalCompositeOperation無効(source-over) ・strengthsの数値に応じてpost処理の負荷がexponentialに増大する(中断不可) ・strengthsに数値以外を指定した場合、該当のstrength=0とする ・非対称averageぼかしの場合、strength<max(x,y)の領域で空白発生の可能性がある ・同様に、ImageDataが欠落する描画canvas境界で空白発生の可能性がある ・空白部分は透明黒色とする |
|
目次
filter 特定項目仕様 |
filter特定項目仕様と付随する留意事項について記述する
Ver.2.44.22以降、post処理の付録機能(未最適化)としてfilterを追加する ・Ver.2.44.23以降、各RGBA値=0で正常に機能しない致命的な不具合を修正 ・Ver.2.46.24以降、HSV-color空間に対応 ・Ver.2.48.25以降、描画canvas境界で正常に機能しない不具合を修正 ・Ver.2.52.25以降、filterを適用するcanvas-areaの設定項目を追加 ・Ver.2.60.27以降、canvas-areaのlimiter-canvas-size(canvas-width,canvas-height)を追加 ・Ver.2.63.27以降、filter適用前後のmask領域を指定するcanvas-maskの設定項目を追加 ・Ver.2.103.33以降、応用例を追記 z入力欄にfilterを入力 filter||FILTER{filters} ・任意位置に挿入可 ・filterはlayer合成後のpost最終処理(svg出力は無効) ・filtersはmask[]area[]filterを適用順にcolon:区切りで入力 ・Ver.2.52.25以降、area[]内datasetは設定値をcomma,区切りで入力(省略時、全体に適用) area[x||0,y||0,w||canvas-width,h||canvas-height] ・canvas-areaは始点(x,y)とarea-size(w,h)を直列化してpx数値で指定する ・Ver.2.60.27以降、下流側で致命的な不具合に繋がる入力を回避 area[0,0,1e13] -> Value is outside the 'long' value range. area[-1e9,,1e9] -> Out of memory at ImageData creation ⇒ area[0,0,canvas-width,canvas-height] ・Ver.2.63.27以降、mask[]内datasetは設定値をcomma,区切りで入力(省略時、全体に適用) mask[Nlegend||last,isInverse||false,isClear||false] ・Nlegend=1~lastはmask領域を指定するplot-lineのlegend番号 範囲外の数値||数値以外を指定した場合、最終legendを選択 ・isInverse=false||trueはmask領域の内外を反転する falseの場合、mask領域の内側のみにfilterを適用 trueの場合、mask領域の外側のみにfilterを適用 ・isClear=false||trueはfilter適用範囲外の処理を選択する falseの場合、filter適用前のRGBA値を保持 trueの場合、透明黒色にRGBA値をclear filterは上下左右対称(2n-1)x(2n-1)sizeの2次元配列を1次元に直列化して定義する ・2次元配列の中央要素をfilter対象pixelとして周囲pixelを含む重みを数値で指定する ・非対称(2n)x(2n)sizeのfilterは対称(2n+1)x(2n+1)sizeを基準に設定する ・filterを適用するRGBAの組合せは任意に選択可(順不同) ・Ver.2.46.24以降、円柱HSV||円錐HSV_coneの組合せを追加 ・RGBA/HSVの組合せを併記した場合、filtering手順を次に示す 最終frameを取得 ⇒ RGB->HSV非線形順変換 ⇒ HSV-color空間でfiltering ⇒ HSV->RGB非線形逆変換 ⇒ RGBA-color空間でfiltering ⇒ 処理結果を出力 Ver.2.44.23以降、irregular入力に対応 r || rr || rrr || r[] || []r || [0]r || [string]r -> r[0] [1]rgb || r[1]gb || rg[1]b -> rgb[1] r[1]g[2]b || g[1]r[2]b || b[1]g[2]r -> rgb[1] []r[1]g[2]b || [0]r[1]g[2]b -> rgb[0] [0xa]r[1]g[2]b[3] -> rgb[10] Ver.2.46.24以降、HSV-color空間に対応 ・円柱model rgba[1]hsv || hsv[1]:rgba[1] -> hsvrgba[1] ・円錐model hsv_cone[1]:rgba[1] -> hsvrgba_cone[1] ・HSV-color空間よりRGBA-color空間を優先する場合 rgba[1]:hsv[1] Ver.2.52.25以降、filterを適用するcanvas-areaの設定項目を追加 ・canvas-areaは始点(x,y)とarea-size(w,h)を直列化してpx数値で指定する area[x||0,y||0,w||canvas-width,h||canvas-height] ・始点(x,y)=(10,20)・area-size(w,h)=(30,40) ⇒ 終点(x,y)=(10+30-1,20+40-1) area[10,20,30,40] 留意事項を列挙する ・svg出力は無効 ・putImageData()同期出力のため、canvas-globalCompositeOperation無効(source-over) ・filter sizeに応じてpost処理の負荷がexponentialに増大する(中断不可) ・加重平均filterは重みを正規化するが、edge抽出filterは正規化しない(白黒飛びを許容) ・ImageDataが欠落する描画canvas境界は加重平均filterとして扱う(意図とは異なる可能性あり) ・canvas-backgroundにtransparent選択の場合、背景色は透明黒色とする ・Ver.2.44.23以降、filter配列要素に数値以外を指定した場合、該当の重み=0とする Ver.2.103.33以降、応用例を列挙する ・3D-LiDAR等のhard技術を代替||補完する物体検出algorithmの検討 ・拡張機能を含むfilterは深層学習の重み関数||bias項||活性化関数に相当 ・robust性を向上する場合、以下の階層を想定して多段階にfilterを適用(順不同) Low-Pass-Filterによるnoise除去(averageぼかし||DFT||DWT) 時間帯等による光学的な補正(非線形なgamma補正||tone-curve調整) 物体検出空間への変換(線形||非線形なcolor空間の変換) sharpness(加重平均) 輪郭抽出(edge抽出) 3D-特徴点抽出(陰影処理||2値化) |
|
目次
filter一覧 |
filterを列挙する
・加重平均 ・edge抽出 ・averageぼかし ・非対称averageぼかし ・Gaussぼかし ・tone-curve ・post-transformer ・post-compressor ・post-processor |
|
目次
加重平均 |
加重平均filterについて記述する
加重平均filterの一例を示す ・RGBA値Gaussian3x3(簡易なGaussぼかし) rgba[1,2,1,2,4,2,1,2,1] ・対象pixelの重みを最大値4として周囲pixelを含む次の重み平均を正規化する [ 1,2,1, 2,4,2, 1,2,1 ] ・RGBA値x方向average3x3 rgba[0,0,0,1,1,1,0,0,0] [ 0,0,0, 1,1,1, 0,0,0 ] ・RGBA値y方向average3x3 rgba[0,1,0,0,1,0,0,1,0] [ 0,1,0, 0,1,0, 0,1,0 ] ・RGBA値x/y方向average3x3 rgba[0,1,0,1,1,1,0,1,0] [ 0,1,0, 1,1,1, 0,1,0 ] ・RGB値average_square3x3 rgb[1,1,1,1,1,1,1,1,1] [ 1,1,1, 1,1,1, 1,1,1 ] ・average_square4x4は定義不可(average_square3x3に同義) rgb[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1] [ 1,1,1, 1,1,1, 1,1,1 ] ・RGB値average_circle3x3 rgb[0,1,0,1,1,1,0,1,0] [ 0,1,0, 1,1,1, 0,1,0 ] ・RGB値sharpness3x3 rgb[-1,-1,-1,-1,9,-1,-1,-1,-1] [ -1,-1,-1, -1,9,-1, -1,-1,-1 ] |
|
目次
edge抽出 |
edge抽出filterについて記述する
edge抽出filter(重みの総和=0)の一例を示す ・RGB値edge3x3 rgb[-1,-1,-1,-1,8,-1,-1,-1,-1] [ -1,-1,-1, -1,8,-1, -1,-1,-1 ] ・R値edge強化3x3 r[-10,-10,-10,-10,80,-10,-10,-10,-10] [ -10,-10,-10, -10,80,-10, -10,-10,-10 ] ・R値Laplacian3x3 r[0,-1,0,-1,4,-1,0,-1,0] [ 0,-1,0, -1,4,-1, 0,-1,0 ] ・G値Laplacian強化3x3 g[0,-10,0,-10,40,-10,0,-10,0] [ 0,-10,0, -10,40,-10, 0,-10,0 ] ・G値emboss3x3 g[-1,0,0,0,1,0,0,0,0] [ -1,0,0, 0,1,0, 0,0,0 ] ・B値emboss強化3x3 b[-10,0,0,0,10,0,0,0,0] [ -10,0,0, 0,10,0, 0,0,0 ] ・B値zero化1x1 b[0] ・S値zero化1x1(monotone化) s[0] || s_cone[0] |
|
目次
average ぼかし |
averageぼかしについて記述する
filterを代用してaverageぼかしを定義する ・単純な加重平均filterとして指向性のblurringに応用する averageぼかしの仕様を列挙する ・ぼかし強度はfilter(N)x(N)sizeのNに比例する ・高速化のため、filter配列要素の重みを0||1で2値化する 2値化の分布形状を固定してN違いのfilter配列を以下の実数演算で生成する ・average_square [N=3,N2=int(N/2),filter=vectorc(N*N), calc_w(s2)=<1, _sir(=<{_sic(=<filter[(ir+N2)*N+(ic+N2)]=calc_w(ir**2+ic**2)=>,-N2,N2)},-N2,N2), =<trans(filter)]=> ・average_circle [N=3,N2=int(N/2),filter=vectorc(N*N), calc_w(s2)=<switch(s2>N2**2,0:1,1), _sir(=<{_sic(=<filter[(ir+N2)*N+(ic+N2)]=calc_w(ir**2+ic**2)=>,-N2,N2)},-N2,N2), =<trans(filter)]=> average_squareのfilter配列を列挙する ・N=1 [ 1 ] ・N=3 [ 1,1,1, 1,1,1, 1,1,1 ] ・N=5 [ 1,1,1,1,1, 1,1,1,1,1, 1,1,1,1,1, 1,1,1,1,1, 1,1,1,1,1 ] ・N=7 [ 1,1,1,1,1,1,1, 1,1,1,1,1,1,1, 1,1,1,1,1,1,1, 1,1,1,1,1,1,1, 1,1,1,1,1,1,1, 1,1,1,1,1,1,1, 1,1,1,1,1,1,1 ] ・N=9 [ 1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1 ] ・N=11 [ 1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1 ] ・N=13 [ 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1 ] ・N=15 [ 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1 ] ・N=17 [ 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1 ] ・N=19 [ 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1 ] ・N=21 [ 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1 ] ・N=23 [ 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1 ] ・N=25 [ 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1 ] ・N=27 [ 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1 ] ・N=29 [ 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1 ] ・N=31 [ 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1 ] ・N=33(以降、内部optionでmatSizeMaxの上限値を解放) [ 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1 ] ・N=35 [ 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1 ] ・N=37 [ 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1 ] ・N=39 [ 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1 ] average_circleのfilter配列を列挙する ・N=1 [ 1 ] ・N=3 [ 0,1,0, 1,1,1, 0,1,0 ] ・N=5 [ 0,0,1,0,0, 0,1,1,1,0, 1,1,1,1,1, 0,1,1,1,0, 0,0,1,0,0 ] ・N=7 [ 0,0,0,1,0,0,0, 0,1,1,1,1,1,0, 0,1,1,1,1,1,0, 1,1,1,1,1,1,1, 0,1,1,1,1,1,0, 0,1,1,1,1,1,0, 0,0,0,1,0,0,0 ] ・N=9 [ 0,0,0,0,1,0,0,0,0, 0,0,1,1,1,1,1,0,0, 0,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,0, 1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,0, 0,0,1,1,1,1,1,0,0, 0,0,0,0,1,0,0,0,0 ] ・N=11 [ 0,0,0,0,0,1,0,0,0,0,0, 0,0,1,1,1,1,1,1,1,0,0, 0,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,0, 1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,0, 0,0,1,1,1,1,1,1,1,0,0, 0,0,0,0,0,1,0,0,0,0,0 ] ・N=13 [ 0,0,0,0,0,0,1,0,0,0,0,0,0, 0,0,0,1,1,1,1,1,1,1,0,0,0, 0,0,1,1,1,1,1,1,1,1,1,0,0, 0,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,0, 1,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,0, 0,0,1,1,1,1,1,1,1,1,1,0,0, 0,0,0,1,1,1,1,1,1,1,0,0,0, 0,0,0,0,0,0,1,0,0,0,0,0,0 ] ・N=15 [ 0,0,0,0,0,0,0,1,0,0,0,0,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,0,0,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,0,0,0,0, 0,0,0,0,0,0,0,1,0,0,0,0,0,0,0 ] ・N=17 [ 0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,1,1,0,0,0,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,0,0,0,1,1,1,1,1,1,1,0,0,0,0,0, 0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0 ] ・N=19 [ 0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,1,1,1,1,0,0,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,1,1,1,1,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0 ] ・N=21 [ 0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0, 0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0 ] ・N=23 [ 0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0, 0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0 ] ・N=25 [ 0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0, 0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0 ] ・N=27 [ 0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0, 0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0 ] ・N=29 [ 0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0, 0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0, 0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0, 0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0 ] ・N=31 [ 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0, 0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0 ] ・N=33(以降、内部optionでmatSizeMaxの上限値を解放) [ 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0, 0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0, 0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0, 0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0 ] ・N=35 [ 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0, 0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0 ] ・N=37 [ 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0, 0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0, 0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0, 0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0 ] ・N=39 [ 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0, 0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0, 0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0, 0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0 ] |
|
目次
非対称 average ぼかし |
非対称averageぼかしについて記述する
filterを代用して非対称averageぼかしを定義する ・単純な加重平均filterとして指向性のblurringに応用する 非対称averageぼかしの仕様を列挙する ・ぼかし強度はfilter(N)x(N)sizeのNに比例する ・高速化のため、filter配列要素の重みを0||1で2値化する 2値化の分布形状を可変してN違いのfilter配列を以下の実数演算で生成する ・average_square [N=13,N2=int(N/2),filter=vectorc(N*N), x=0,y=0,k=1,rad=0, rotz_LHS(psi)=<{rt=real(psi),=<(cos(rt),sin(rt),:-sin(rt),cos(rt),:,,1)}=>, Rz=rotz_LHS(rad)=>, isOutOfArea(x)=<(x[0]**2>N2**2)|((x[1]*k)**2>N2**2), calc_w(ir,ic)=<switch(isOutOfArea(=<Rz*{ic-x,ir-y,1})=>,0:1,1), _sir(=<{_sic(=<filter[(ir+N2)*N+(ic+N2)]=calc_w(ir,ic)=>,-N2,N2)},-N2,N2), =<trans(filter)]=> ・average_circle [N=13,N2=int(N/2),filter=vectorc(N*N), x=0,y=0,k=1,rad=0, rotz_LHS(psi)=<{rt=real(psi),=<(cos(rt),sin(rt),:-sin(rt),cos(rt),:,,1)}=>, Rz=rotz_LHS(rad)=>, isOutOfArea(x)=<x[0]**2+(x[1]*k)**2>N2**2, calc_w(ir,ic)=<switch(isOutOfArea(=<Rz*{ic-x,ir-y,1})=>,0:1,1), _sir(=<{_sic(=<filter[(ir+N2)*N+(ic+N2)]=calc_w(ir,ic)=>,-N2,N2)},-N2,N2), =<trans(filter)]=> filter配列生成の各設定値の定義を列挙する ・(x,y)は対象pixelに対する回転中心の相対座標のpx数値 ・kは非対称性を作るy方向の比例係数の実数値 ・radは分布を回転する回転行列の弧度数値 average_asym_square13x13のfilter配列を列挙する ・基準(x,y,k,rad)=(0,0,1,0) [ 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1 ] ・(x,y,k,rad)=(0,0,0,0) [ 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1 ] ・(x,y,k,rad)=(1,2,0,0) [ 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1 ] ・(x,y,k,rad)=(1,2,0.5,0) [ 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1 ] ・(x,y,k,rad)=(1,2,1,0) [ 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1 ] ・(x,y,k,rad)=(1,2,1.5,0) [ 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1 ] ・(x,y,k,rad)=(1,2,2,0) [ 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,0,0,0,0,0,0,0,0,0,0,0,0 ] ・(x,y,k,rad)=(1,2,3,0) [ 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0 ] ・(x,y,k,rad)=(1,2,3,pi/4) [ 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,1,0,0,0,0,0,0,0,0, 0,0,0,1,1,1,0,0,0,0,0,0,0, 0,0,1,1,1,1,1,0,0,0,0,0,0, 0,0,0,1,1,1,1,1,0,0,0,0,0, 0,0,0,0,1,1,1,1,1,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,0,0,0, 0,0,0,0,0,0,1,1,1,1,1,0,0, 0,0,0,0,0,0,0,1,1,1,1,1,0, 0,0,0,0,0,0,0,0,1,1,1,1,1, 0,0,0,0,0,0,0,0,0,1,1,1,0 ] ・(x,y,k,rad)=(1,2,3,pi/2) [ 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,1,1,1,1,0,0,0,0, 0,0,0,0,0,1,1,1,1,0,0,0,0, 0,0,0,0,0,1,1,1,1,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,0,0,0, 0,0,0,0,0,1,1,1,1,1,0,0,0, 0,0,0,0,0,1,1,1,1,1,0,0,0, 0,0,0,0,0,1,1,1,1,1,0,0,0, 0,0,0,0,0,1,1,1,1,1,0,0,0, 0,0,0,0,0,1,1,1,1,1,0,0,0, 0,0,0,0,0,1,1,1,1,1,0,0,0, 0,0,0,0,0,0,1,1,1,1,0,0,0 ] ・(x,y,k,rad)=(0,0,3,pi/2) [ 0,0,0,0,1,1,1,1,0,0,0,0,0, 0,0,0,0,1,1,1,1,0,0,0,0,0, 0,0,0,0,1,1,1,1,0,0,0,0,0, 0,0,0,0,1,1,1,1,1,0,0,0,0, 0,0,0,0,1,1,1,1,1,0,0,0,0, 0,0,0,0,1,1,1,1,1,0,0,0,0, 0,0,0,0,1,1,1,1,1,0,0,0,0, 0,0,0,0,1,1,1,1,1,0,0,0,0, 0,0,0,0,1,1,1,1,1,0,0,0,0, 0,0,0,0,1,1,1,1,1,0,0,0,0, 0,0,0,0,0,1,1,1,1,0,0,0,0, 0,0,0,0,0,1,1,1,1,0,0,0,0, 0,0,0,0,0,1,1,1,1,0,0,0,0 ] ・(x,y,k,rad)=(0,0,3,3pi/4) [ 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,1,0,0,0, 0,0,0,0,0,0,0,0,1,1,1,0,0, 0,0,0,0,0,0,0,1,1,1,1,1,0, 0,0,0,0,0,0,1,1,1,1,1,0,0, 0,0,0,0,0,1,1,1,1,1,0,0,0, 0,0,0,0,1,1,1,1,1,0,0,0,0, 0,0,0,1,1,1,1,1,0,0,0,0,0, 0,0,1,1,1,1,1,0,0,0,0,0,0, 0,1,1,1,1,1,0,0,0,0,0,0,0, 0,0,1,1,1,0,0,0,0,0,0,0,0, 0,0,0,1,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0 ] ・(x,y,k,rad)=(0,0,3,pi) [ 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0 ] ・(x,y,k,rad)=(0,0,5,pi) [ 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0 ] ・(x,y,k,rad)=(0,0,7,pi) [ 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 1,1,1,1,1,1,1,1,1,1,1,1,1, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0 ] average_asym_circle13x13のfilter配列を列挙する ・基準(x,y,k,rad)=(0,0,1,0) [ 0,0,0,0,0,0,1,0,0,0,0,0,0, 0,0,0,1,1,1,1,1,1,1,0,0,0, 0,0,1,1,1,1,1,1,1,1,1,0,0, 0,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,0, 1,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,0, 0,1,1,1,1,1,1,1,1,1,1,1,0, 0,0,1,1,1,1,1,1,1,1,1,0,0, 0,0,0,1,1,1,1,1,1,1,0,0,0, 0,0,0,0,0,0,1,0,0,0,0,0,0 ] ・(x,y,k,rad)=(0,0,0,0) [ 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,1,1,1,1,1,1,1,1 ] ・(x,y,k,rad)=(1,2,0,0) [ 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1 ] ・(x,y,k,rad)=(1,2,0.5,0) [ 0,0,0,1,1,1,1,1,1,1,1,1,0, 0,0,0,1,1,1,1,1,1,1,1,1,0, 0,0,1,1,1,1,1,1,1,1,1,1,1, 0,0,1,1,1,1,1,1,1,1,1,1,1, 0,0,1,1,1,1,1,1,1,1,1,1,1, 0,0,1,1,1,1,1,1,1,1,1,1,1, 0,0,1,1,1,1,1,1,1,1,1,1,1, 0,0,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,0,1,1,1,1,1,1,1,1,1,1,1, 0,0,1,1,1,1,1,1,1,1,1,1,1, 0,0,1,1,1,1,1,1,1,1,1,1,1, 0,0,1,1,1,1,1,1,1,1,1,1,1 ] ・(x,y,k,rad)=(1,2,1,0) [ 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,1,0,0,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,0, 0,0,1,1,1,1,1,1,1,1,1,1,1, 0,0,1,1,1,1,1,1,1,1,1,1,1, 0,0,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,0,1,1,1,1,1,1,1,1,1,1,1, 0,0,1,1,1,1,1,1,1,1,1,1,1, 0,0,1,1,1,1,1,1,1,1,1,1,1, 0,0,0,1,1,1,1,1,1,1,1,1,0 ] ・(x,y,k,rad)=(1,2,1.5,0) [ 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,1,0,0,0,0,0, 0,0,0,0,1,1,1,1,1,1,1,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1, 0,0,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,0,1,1,1,1,1,1,1,1,1,1,1, 0,0,1,1,1,1,1,1,1,1,1,1,1, 0,0,0,0,1,1,1,1,1,1,1,0,0, 0,0,0,0,0,0,0,1,0,0,0,0,0 ] ・(x,y,k,rad)=(1,2,2,0) [ 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,1,0,0,0,0,0, 0,0,0,1,1,1,1,1,1,1,1,1,0, 0,0,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,0,1,1,1,1,1,1,1,1,1,1,1, 0,0,0,1,1,1,1,1,1,1,1,1,0, 0,0,0,0,0,0,0,1,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0 ] ・(x,y,k,rad)=(1,2,3,0) [ 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,1,0,0,0,0,0, 0,0,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,1, 0,0,1,1,1,1,1,1,1,1,1,1,1, 0,0,0,0,0,0,0,1,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0 ] ・(x,y,k,rad)=(1,2,3,pi/4) [ 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,1,1,1,0,0,0,0,0,0,0, 0,0,0,1,1,1,1,0,0,0,0,0,0, 0,0,0,1,1,1,1,1,0,0,0,0,0, 0,0,0,0,1,1,1,1,1,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,0,0,0, 0,0,0,0,0,0,1,1,1,1,1,0,0, 0,0,0,0,0,0,0,1,1,1,1,1,0, 0,0,0,0,0,0,0,0,1,1,1,1,0, 0,0,0,0,0,0,0,0,0,1,1,1,0 ] ・(x,y,k,rad)=(1,2,3,pi/2) [ 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,1,0,0,0,0,0, 0,0,0,0,0,0,1,1,1,0,0,0,0, 0,0,0,0,0,0,1,1,1,0,0,0,0, 0,0,0,0,0,0,1,1,1,0,0,0,0, 0,0,0,0,0,0,1,1,1,0,0,0,0, 0,0,0,0,0,0,1,1,1,0,0,0,0, 0,0,0,0,0,1,1,1,1,1,0,0,0, 0,0,0,0,0,0,1,1,1,0,0,0,0, 0,0,0,0,0,0,1,1,1,0,0,0,0, 0,0,0,0,0,0,1,1,1,0,0,0,0, 0,0,0,0,0,0,1,1,1,0,0,0,0 ] ・(x,y,k,rad)=(0,0,3,pi/2) [ 0,0,0,0,0,0,1,0,0,0,0,0,0, 0,0,0,0,0,1,1,1,0,0,0,0,0, 0,0,0,0,0,1,1,1,0,0,0,0,0, 0,0,0,0,0,1,1,1,0,0,0,0,0, 0,0,0,0,0,1,1,1,0,0,0,0,0, 0,0,0,0,0,1,1,1,0,0,0,0,0, 0,0,0,0,1,1,1,1,1,0,0,0,0, 0,0,0,0,0,1,1,1,0,0,0,0,0, 0,0,0,0,0,1,1,1,0,0,0,0,0, 0,0,0,0,0,1,1,1,0,0,0,0,0, 0,0,0,0,0,1,1,1,0,0,0,0,0, 0,0,0,0,0,1,1,1,0,0,0,0,0, 0,0,0,0,0,0,1,0,0,0,0,0,0 ] ・(x,y,k,rad)=(0,0,3,3pi/4) [ 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,1,1,1,0,0, 0,0,0,0,0,0,0,1,1,1,1,0,0, 0,0,0,0,0,0,1,1,1,1,1,0,0, 0,0,0,0,0,1,1,1,1,1,0,0,0, 0,0,0,0,1,1,1,1,1,0,0,0,0, 0,0,0,1,1,1,1,1,0,0,0,0,0, 0,0,1,1,1,1,1,0,0,0,0,0,0, 0,0,1,1,1,1,0,0,0,0,0,0,0, 0,0,1,1,1,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0 ] ・(x,y,k,rad)=(0,0,3,pi) [ 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,1,0,0,0,0,0,0, 0,1,1,1,1,1,1,1,1,1,1,1,0, 1,1,1,1,1,1,1,1,1,1,1,1,1, 0,1,1,1,1,1,1,1,1,1,1,1,0, 0,0,0,0,0,0,1,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0 ] ・(x,y,k,rad)=(0,0,5,pi) [ 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,1,1,1,1,1,1,1,0,0,0, 1,1,1,1,1,1,1,1,1,1,1,1,1, 0,0,0,1,1,1,1,1,1,1,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0 ] ・(x,y,k,rad)=(0,0,7,pi) [ 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 1,1,1,1,1,1,1,1,1,1,1,1,1, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0,0,0 ] |
|
目次
Gauss ぼかし |
Gaussぼかしについて記述する
filterを代用してGaussぼかしを再現する ・高速なblurringの加重平均filterとして多用されるが、仕様上、高速化の恩恵は受けられない Gaussぼかしの仕様を列挙する ・Gauss分布の再現精度はfilter(N)x(N)sizeのNに依存する ・ぼかし強度はfilterの適用回数で変更する(例えば、post-transformer参照) σ=1pxの分布関数を固定してN違いのfilter配列を以下の実数演算で生成する ・簡易なGaussぼかしの場合、配列要素の重みを丸める(量子化bit数=N-1を仮定) [N=3,N2=int(N/2),filter=vectorc(N*N),Nbit=N-1,wmax=2**Nbit, calc_w(s2)=<round(wmax*exp(-0.5*s2)), _sir(=<{_sic(=<filter[(ir+N2)*N+(ic+N2)]=calc_w(ir**2+ic**2)=>,-N2,N2)},-N2,N2), =<trans(filter)]=> ・厳密なGaussぼかしの場合、配列要素の重みを丸めない [N=3,N2=int(N/2),filter=vectorc(N*N), calc_w(s2)=<exp(-0.5*s2), _sir(=<{_sic(=<filter[(ir+N2)*N+(ic+N2)]=calc_w(ir**2+ic**2)=>,-N2,N2)},-N2,N2), =<trans(filter)]=> 簡易なGaussぼかしのfilter配列を列挙する ・N=1 [ 1 ] ・N=3 [ 1,2,1, 2,4,2, 1,2,1 ] ・N=5 [ 0,1,2,1,0, 1,6,10,6,1, 2,10,16,10,2, 1,6,10,6,1, 0,1,2,1,0 ] ・N=7 [ 0,0,0,1,0,0,0, 0,1,5,9,5,1,0, 0,5,24,39,24,5,0, 1,9,39,64,39,9,1, 0,5,24,39,24,5,0, 0,1,5,9,5,1,0, 0,0,0,1,0,0,0 ] ・N=9 [ 0,0,0,0,0,0,0,0,0, 0,0,0,2,3,2,0,0,0, 0,0,5,21,35,21,5,0,0, 0,2,21,94,155,94,21,2,0, 0,3,35,155,256,155,35,3,0, 0,2,21,94,155,94,21,2,0, 0,0,5,21,35,21,5,0,0, 0,0,0,2,3,2,0,0,0, 0,0,0,0,0,0,0,0,0 ] ・N=11 [ 0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0, 0,0,0,2,7,11,7,2,0,0,0, 0,0,2,19,84,139,84,19,2,0,0, 0,0,7,84,377,621,377,84,7,0,0, 0,0,11,139,621,1024,621,139,11,0,0, 0,0,7,84,377,621,377,84,7,0,0, 0,0,2,19,84,139,84,19,2,0,0, 0,0,0,2,7,11,7,2,0,0,0, 0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,0,0,0 ] 厳密なGaussぼかしのfilter配列を列挙する ・N=1 [ 1 ] ・N=3 [ 0.36787944117144233,0.6065306597126334,0.36787944117144233, 0.6065306597126334,1,0.6065306597126334, 0.36787944117144233,0.6065306597126334,0.36787944117144233 ] ・N=5 [ 0.01831563888873418,0.0820849986238988,0.1353352832366127, 0.0820849986238988,0.01831563888873418, 0.0820849986238988,0.36787944117144233,0.6065306597126334, 0.36787944117144233,0.0820849986238988, 0.1353352832366127,0.6065306597126334,1, 0.6065306597126334,0.1353352832366127, 0.0820849986238988,0.36787944117144233,0.6065306597126334, 0.36787944117144233,0.0820849986238988, 0.01831563888873418,0.0820849986238988,0.1353352832366127, 0.0820849986238988,0.01831563888873418 ] ・N=7 [ 0.00012340980408667956,0.0015034391929775724,0.006737946999085467, 0.011108996538242306,0.006737946999085467,0.0015034391929775724, 0.00012340980408667956, 0.0015034391929775724,0.01831563888873418,0.0820849986238988, 0.1353352832366127,0.0820849986238988,0.01831563888873418, 0.0015034391929775724, 0.006737946999085467,0.0820849986238988,0.36787944117144233, 0.6065306597126334,0.36787944117144233,0.0820849986238988, 0.006737946999085467, 0.011108996538242306,0.1353352832366127,0.6065306597126334, 1,0.6065306597126334,0.1353352832366127, 0.011108996538242306, 0.006737946999085467,0.0820849986238988,0.36787944117144233, 0.6065306597126334,0.36787944117144233,0.0820849986238988, 0.006737946999085467, 0.0015034391929775724,0.01831563888873418,0.0820849986238988, 0.1353352832366127,0.0820849986238988,0.01831563888873418, 0.0015034391929775724, 0.00012340980408667956,0.0015034391929775724,0.006737946999085467, 0.011108996538242306,0.006737946999085467,0.0015034391929775724, 0.00012340980408667956 ] ・N=9 [ 1.1253517471925912e-7,0.000003726653172078671,0.00004539992976248485, 0.00020346836901064417,0.00033546262790251185,0.00020346836901064417, 0.00004539992976248485,0.000003726653172078671,1.1253517471925912e-7, 0.000003726653172078671,0.00012340980408667956,0.0015034391929775724, 0.006737946999085467,0.011108996538242306,0.006737946999085467, 0.0015034391929775724,0.00012340980408667956,0.000003726653172078671, 0.00004539992976248485,0.0015034391929775724,0.01831563888873418, 0.0820849986238988,0.1353352832366127,0.0820849986238988, 0.01831563888873418,0.0015034391929775724,0.00004539992976248485, 0.00020346836901064417,0.006737946999085467,0.0820849986238988, 0.36787944117144233,0.6065306597126334,0.36787944117144233, 0.0820849986238988,0.006737946999085467,0.00020346836901064417, 0.00033546262790251185,0.011108996538242306,0.1353352832366127, 0.6065306597126334,1,0.6065306597126334, 0.1353352832366127,0.011108996538242306,0.00033546262790251185, 0.00020346836901064417,0.006737946999085467,0.0820849986238988, 0.36787944117144233,0.6065306597126334,0.36787944117144233, 0.0820849986238988,0.006737946999085467,0.00020346836901064417, 0.00004539992976248485,0.0015034391929775724,0.01831563888873418, 0.0820849986238988,0.1353352832366127,0.0820849986238988, 0.01831563888873418,0.0015034391929775724,0.00004539992976248485, 0.000003726653172078671,0.00012340980408667956,0.0015034391929775724, 0.006737946999085467,0.011108996538242306,0.006737946999085467, 0.0015034391929775724,0.00012340980408667956,0.000003726653172078671, 1.1253517471925912e-7,0.000003726653172078671,0.00004539992976248485, 0.00020346836901064417,0.00033546262790251185,0.00020346836901064417, 0.00004539992976248485,0.000003726653172078671,1.1253517471925912e-7 ] ・N=11 [ 1.3887943864964021e-11,1.2501528663867426e-9,4.139937718785167e-8, 5.04347662567888e-7,0.0000022603294069810542,0.000003726653172078671, 0.0000022603294069810542,5.04347662567888e-7,4.139937718785167e-8, 1.2501528663867426e-9,1.3887943864964021e-11, 1.2501528663867426e-9,1.1253517471925912e-7,0.000003726653172078671, 0.00004539992976248485,0.00020346836901064417,0.00033546262790251185, 0.00020346836901064417,0.00004539992976248485,0.000003726653172078671, 1.1253517471925912e-7,1.2501528663867426e-9, 4.139937718785167e-8,0.000003726653172078671,0.00012340980408667956, 0.0015034391929775724,0.006737946999085467,0.011108996538242306, 0.006737946999085467,0.0015034391929775724,0.00012340980408667956, 0.000003726653172078671,4.139937718785167e-8, 5.04347662567888e-7,0.00004539992976248485,0.0015034391929775724, 0.01831563888873418,0.0820849986238988,0.1353352832366127, 0.0820849986238988,0.01831563888873418,0.0015034391929775724, 0.00004539992976248485,5.04347662567888e-7, 0.0000022603294069810542,0.00020346836901064417,0.006737946999085467, 0.0820849986238988,0.36787944117144233,0.6065306597126334, 0.36787944117144233,0.0820849986238988,0.006737946999085467, 0.00020346836901064417,0.0000022603294069810542, 0.000003726653172078671,0.00033546262790251185,0.011108996538242306, 0.1353352832366127,0.6065306597126334,1, 0.6065306597126334,0.1353352832366127,0.011108996538242306, 0.00033546262790251185,0.000003726653172078671, 0.0000022603294069810542,0.00020346836901064417,0.006737946999085467, 0.0820849986238988,0.36787944117144233,0.6065306597126334, 0.36787944117144233,0.0820849986238988,0.006737946999085467, 0.00020346836901064417,0.0000022603294069810542, 5.04347662567888e-7,0.00004539992976248485,0.0015034391929775724, 0.01831563888873418,0.0820849986238988,0.1353352832366127, 0.0820849986238988,0.01831563888873418,0.0015034391929775724, 0.00004539992976248485,5.04347662567888e-7, 4.139937718785167e-8,0.000003726653172078671,0.00012340980408667956, 0.0015034391929775724,0.006737946999085467,0.011108996538242306, 0.006737946999085467,0.0015034391929775724,0.00012340980408667956, 0.000003726653172078671,4.139937718785167e-8, 1.2501528663867426e-9,1.1253517471925912e-7,0.000003726653172078671, 0.00004539992976248485,0.00020346836901064417,0.00033546262790251185, 0.00020346836901064417,0.00004539992976248485,0.000003726653172078671, 1.1253517471925912e-7,1.2501528663867426e-9, 1.3887943864964021e-11,1.2501528663867426e-9,4.139937718785167e-8, 5.04347662567888e-7,0.0000022603294069810542,0.000003726653172078671, 0.0000022603294069810542,5.04347662567888e-7,4.139937718785167e-8, 1.2501528663867426e-9,1.3887943864964021e-11 ] |
|
目次
tone-curve 特定項目仕様 |
tone-curve特定項目仕様について記述する
Ver.2.47.24以降、filterを代用してgamma補正を含むtone-curve調整機能を追加する tone-curveの仕様を列挙する ・filter定義(配列length=1~4) hsvrgba[slope,offset||0,gamma||1,threshold||th=0~255||0] ・べき乗則のgamma値を拡張して連続的なtone-curveに一般化する定義式を次に示す t=hsvrgba t0=switch(t-th<0,0:1,255) t=pow((t-th)/switch(t0-th==0,1:1,t0-th),gamma)*(t0-th)+th ・Ver.2.59.26以降、論理演算子を追加 t=pow((t-th)/(t0-th||1),gamma)*(t0-th)+th ・tone-curve調整後、一次変換 t=t*slope+offset ・slope=-1の場合、反転を定義 offset=offset+255 -> t=-t+offset+255 test caseを列挙する ・R値係数倍(=R*2) r[2] ・R値反転(=-R+255) r[-1] ・R値一次変換(=R*2+50) r[2,50] ・R値反転一次変換(=-R+255+50) r[-1,50] ・sepia-tone化 r[0.9]:g[0.7]:b[0.4] ・相対輝度Y値化(輝度の可視化) r[0.2126]:g[0.7152]:b[0.0722] ・NTSC加重平均法の輝度Y'値化 r[0.29891]:g[0.58661]:b[0.11448] ・下凸のgamma補正 [1,,2,0] [1,,0.5,255] ・上凸のgamma補正 [1,,0.5,0] [1,,2,255] ・S字のtone-curve調整 [1,,0.5,128] [1,,2,128] 留意事項を列挙する ・A値=255の反転は無効(rgba[-1]の反転後、A=0のputImageData()でRGB値=0のNative仕様) |
|
目次
post -transformer 特定項目仕様 |
post-transformer特定項目仕様と付随する留意事項について記述する
Ver.2.54.26以降、filterを代用してtransform同等のpost-transformerを追加する post-transformerの仕様を列挙する ・filter定義(配列length=6~7) rgba[a,b,c,d,e,f,isForward||0] ・配列はcanvas座標変換ctx.setTransform(a,b,c,d,e,f)の引数をcomma,区切りで入力 ・各引数の詳細はtransform参照 ・isForward=0||1は座標変換後の各RGBA値の代入方法を数値で指定する 0の場合、canvas座標を逆変換して変換前の各RGBA値を参照して代入 1の場合、canvas座標を順変換して変換前の各RGBA値を成行きで上書き代入 ・座標変換の原点はcanvas-areaの始点とする test caseを列挙する ・canvas全体のRGBA値に簡易なGaussぼかしを適用後、座標変換を適用 area[0]rgba[1,2,1,2,4,2,1,2,1]:area[0]rgba[1,0.1,-0.5,0.5,65,40] ・canvas全体のRGBA値に座標変換を適用後、簡易なGaussぼかしを適用 area[0]rgba[1,0.1,-0.5,0.5,65,40]:area[0]rgba[1,2,1,2,4,2,1,2,1] ・canvas全体のRGBA値に簡易なGaussぼかしを3回適用後、座標変換を適用 rgba[1,2,1,2,4,2,1,2,1]:rgba[1,2,1,2,4,2,1,2,1]:rgba[1,2,1,2,4,2,1,2,1]:rgba[1,0.1,-0.5,0.5,65,40] ・canvas全体のRGBA値に座標変換を適用後、簡易なGaussぼかしを3回適用 rgba[1,0.1,-0.5,0.5,65,40]:rgba[1,2,1,2,4,2,1,2,1]:rgba[1,2,1,2,4,2,1,2,1]:rgba[1,2,1,2,4,2,1,2,1] ・canvas-area[30,30]のRGBA値に座標変換を適用 area[30,30]rgba[1,0.1,-0.5,0.5,65,40] ・canvas全体のRGBA値に拡大の順変換を適用(Braun管のdisplay表示を模擬) area[0]rgba[2,0,0,2,0,0,1] 留意事項を列挙する ・変換後のcanvas座標を丸めるため、transformよりRGBA値の補間精度が悪化する ・順変換の場合、等倍でも空白発生の可能性がある(例えば、rgba[1,0.1,-0.5,1,0,0,1]) ・空白部分は透明黒色とする ・別途、blurringのみをtransformの対象とする場合、plot点に右手系の座標変換を適用する 左手系のcanvas座標変換と等価変換は困難のため、例えば、transform3x3をplot点に演算 |
|
目次
post -compressor 特定項目仕様 |
post-compressor特定項目仕様と付随する留意事項について記述する
Ver.2.65.27以降、filterを代用してpost-compressor(noise処理等、情報量の圧縮機能)を追加 ・Ver.2.72.29以降、離散Wavelet変換を追加 post-compressorの仕様を列挙する ・hsvlrgba||HSVLRGBAのalphabetを除外してpost-compressor処理名を定義する ・post-compressor処理は単独処理で処理名の併記不可 post-compressor処理を優先順に列挙する ・高速Fourier変換は不採用(filter代用の仕様上、overhead大) ・離散Fourier変換 dft_rgba[cutoffU=0~1||0,cutoffV=0~1||0] ・離散Wavelet変換 Ver.2.72.29以降、追加 dwt_rgba[cutoffU=0~1||0,cutoffV=0~1||0] 留意事項を列挙する ・cutoffU/Vは高周波数側の2次元AND領域の情報をnoiseとして強制的に遮断する 離散Fourier変換の場合、spectrum強度=0 離散Wavelet変換の場合、wavelet情報=0 ・離散Wavelet変換の場合、area-size(w,h)=(2^p,2^q)を規定する(切捨て側に自動re-size) ・未最適化のため、下流側でarea-size(w,h<=256)を制限する memory size<100MB ・canvas全体に適用する場合、canvas-areaを変えて列挙する dft_rgba[0.05,0.05]:area[256,0]dft_rgba[0.05,0.05] dwt_rgba[0.05,0.05]:area[256,0]dwt_rgba[0.05,0.05] |
|
目次
post -processor 特定項目仕様 |
post-processor特定項目仕様について記述する
Ver.2.48.24以降、filterを代用してpost-processorを追加する ・Ver.2.48.25以降、描画canvas境界で正常に機能しないmosaic化の不具合を修正 ・Ver.2.49.25以降、2値化||monotone化(輝度)のsw=-1任意のRGB重み平均値に対応 ・Ver.2.61.27以降、塗りつぶし機能を追加(Nwrapを周回数とする独自の回り込み方式) ・Ver.2.62.27以降、不可逆なencode機能を追加(乱数seed値不定のFisher-Yates shuffle) post-processorの仕様を列挙する ・hsvlrgba||HSVLRGBAのalphabetを除外してpost-processor処理名を定義する ・post-processor処理は単独処理で処理名の併記不可 post-processor処理を優先順に列挙する ・左右反転 fx_rgba[offsetX||0] ・上下反転 fy_rgba[offsetY||0] ・mosaic化(不可逆な平均値化) dot_rgba[dx=1~||1,dy=1~||dx] ・不可逆なencode encode_rgba[dx=1~||1,dy=1~||dx] ・塗りつぶし(fill-inをfiinと省略する) fiin[targetX||0,targetY||0,color,Nwrap=1~256||1] fiin[targetX||0,targetY||0,pickedX||0,pickedY||0,Nwrap=1~256||1] ・Ver.2.120.34以降、RGBA値の指定方法を追加(color入力仕様の留意事項参照) fiin[targetX||0,targetY||0,R=0~255||0,G=0~255||0,B=0~255||0,A=0~255||0,Nwrap=1~256||1] ・2値化(各RGBA値) to2_rgba[threshold=0~255||0] ・2値化(輝度) to2[threshold=0~255||0,sw=-1~6||0,wr,wg,wb] ・monotone化(輝度) mono[sw=-1~6||0,wr,wg,wb] 2値化||monotone化の輝度選択switch sw=0: NTSC加重平均法の輝度Y'=0.29891*r+0.58661*g+0.11448*b sw=1: 相対輝度Y=0.2126*r+0.7152*g+0.0722*b sw=2: HSL-color空間の輝度L=(min+max)/2 sw=3: RGB平均値average=(r+g+b)/3 sw=4: RGB最小値min sw=5: RGB最大値max||HSV-color空間の明度V sw=6: RGB中央値median Ver.2.49.25以降 sw=-1: 任意のRGB重み平均値average=(wr*r+wg*g+wb*b)/(wr+wg+wb||1) test caseを列挙する ・R値右移動100px fx_r:fx_r[100] ・G値上移動100px fy_g:fy_g[-100] ・RGBA値上下左右反転 fy_rgba:fx_rgba ・不可逆なencode encode_rgba[6,3] encode_r[6,3]:encode_g[6,3]:encode_b[6,3]:encode_a[6,3] encode_rgba[256,256] encode_r[256,256]:encode_g[256,256]:encode_b[256,256]:encode_a[256,256] ・color指定で絶対始点(0px,0px)の塗りつぶし fiin[0,0,yellow,8] fiin[0,0,green,8] fiin[0,0,#0123,8] || fiin[0,0,#00112233,8] ・area[30,30]基準のcolor-picked相対位置(10px,10px)指定で相対始点(0px,0px)の塗りつぶし area[30,30]fiin[0,0,10,10,8] ・monotone化(Y'値) mono[-1,0.29891,0.58661,0.11448] ・monotone化(Y値) mono[-1,0.2126,0.7152,0.0722] ・白黒の2値化(edge抽出:monotone化:2値化:RGB反転) rgb[-1,-1,-1,-1,8,-1,-1,-1,-1]:mono[0]:to2_rgba[111]:rgb[-1] rgb[-1,-1,-1,-1,8,-1,-1,-1,-1]:s[0]:to2_rgba[111]:rgb[-1] 留意事項を列挙する ・comma,区切りの場合、rgba()入力のcolor指定不可 |
|
目次
encode仕様 |
post-processor特定項目のencode仕様について記述する
Ver.2.62.27以降、post-processorに不可逆なencode機能を追加する ・noise付与に代用(Ver.2.72.29追記) encodeの仕様/補足を列挙する ・transposition方式 通常、直列化した任意dataを可逆的な規則性に従って並び替える ・理想的なrandom-sortのFisher-Yates shuffle 確率抽選の反復sortのため、一様乱数の前提で完全random性を数学的に保証する ・乱数seed値不定の仕様上、不可逆 decodeする場合、encodeの乱数seed値を連番等で指定する(sort規則を予め指定する) |
|
目次
tile 特定項目仕様 |
tile特定項目仕様について記述する
Ver.2.68.27以降、指定領域の千鳥格子tile機能を追加する z入力欄にtileを入力 tile||TILE{args} ・任意位置に挿入可 ・tileはfiltering直後のpost最終処理(svg出力は無効) ・argsはtile領域を指定する条件をcomma,区切りで入力 tile{dx||1,dy||1,x0||0,y0||0,x1||0,y1||0} ・(dx,dy=1~256)は格子1/格子2のtile-size(w,h)をpx数値で指定する ・(x0,y0=-32768~32767)は格子1のcanvas座標の始点(x,y)をpx数値で指定する 描画canvas境界外の座標を指定した場合、境界外の領域は透明黒色 ・(x1,y1=-32768~32767)は格子2のcanvas座標の始点(x,y)をpx数値で指定する 描画canvas境界外の座標を指定した場合、境界外の領域は透明黒色 |
|
目次
cut 特定項目仕様 |
cut特定項目仕様について記述する
Ver.2.63.27以降、指定領域のcut機能を追加する z入力欄にcutを入力 cut||CUT{args} ・任意位置に挿入可 ・cutはfiltering直後のpost最終処理(svg出力はlayer合成) ・argsはcut領域を指定する条件をcomma,区切りで入力 cut{Nlegend||last,withTransform||false} ・Nlegend=1~lastはcut領域を指定するplot-lineのlegend番号 範囲外の数値||数値以外を指定した場合、最終legendを選択 ・withTransform=false||trueはtransformの反映を選択する svg出力の場合、withBackground=1のみ有効 |
|
目次
v入力仕様 |
v入力仕様と付随する留意事項について記述する
Ver.2.105.33以降、z入力欄の直下に追加 ・Ver.2.319.77以降、vx入力の仕様変更(legend1番で共通 ⇒ 各legendで独立) ・Ver.2.327.79以降、各legendのplot点数が異なることで発生するplot-button実行中断の不具合を修正 Ver.2.328.80以降、同上の追加修正 Ver.2.337.82以降、同上の追加修正(全点のplot||csv出力を保証) ・Ver.2.328.79以降、csv出力の要素の値がNaNの場合、空要素に変換 ・Ver.2.328.79以降、(vx連番,vy連番)のcsv出力に対応 v入力仕様について記述する ・v-checkboxはv入力を選択 ・vx入力欄にx軸の変数名symbol(列vector)を入力 ・vy入力欄にy軸の変数名symbol(列vector)を入力 ・vz入力欄にz軸の変数名symbol(空欄||1~2列の行列)を入力 空欄の場合、(x,y)の散布図 1列の場合、(x,y)におけるzのscalar分布 2列の場合、(x,y)におけるzのvector分布 留意事項を列挙する ・ |
|
目次
layer 描画順 |
layer描画順と付随する留意事項について記述する
描画canvasのlayerを描画順に列挙する ・Ver.2.66.27以降 最背面固定layer(透明黒色の初期状態を表す千鳥格子の描画用) ・background-layer ・grid-layer ・plot-layer ・layer合成用layer ・最前面固定layer(mouse||touchによる範囲選択領域の描画用) 留意事項を列挙する ・最背面/最前面固定layerはpng||svg出力対象外 |
|
目次
背景 優先順 |
背景優先順について記述する
background-layerに背景画像file||color指定値を適用する項目を優先順に列挙する ・bg-image-file@plot-config(svg出力は無効・Internet Explorer非対応) ・bgcolor特定項目指定値 ・bg-color@plot-config入力値 ・canvas-background@plot-config選択値 |
|
目次
grid-layer 描画順 |
grid-layer描画順について記述する
grid-layerに描画する項目を描画順に列挙する ・graph-title ・axis-labels ・origin-label/origin-line ・grid-lines/axis-values grid-layerにcolor指定値を適用する項目を優先順に列挙する ・gdcolor特定項目指定値 ・grid-line-color@plot-config入力値 |
|
目次
plot-layer 描画順 |
plot-layer描画順について記述する
plot-layerに描画する項目を描画順に列挙する ・gradation ・plot-lines ・plot-markers ・legends ・string-path Ver.2.37.18以降、graph-titleはgrid-layerに描画 |
|
目次
post 処理順 |
post処理順について記述する
post処理を処理順に列挙する ・layer合成 ・post最終処理 |
|
目次
layer 合成順 |
layer合成順と付随する留意事項について記述する
svg出力の場合、同期処理をlayer合成順に列挙する ・layerをclear ・同layerにtransformを適用(withBackground=1の場合) ・同layerにbackground-layerを合成(source-over・背景image-file無効) ・同layerにtransformを適用(withBackground=0の場合) ・同layerにgrid-layerを合成(source-over) ・同layerにplot-layerを合成(source-over) ・同layerにcutを適用(transformを反映する場合、withBackground=1のみ有効) png出力||描画canvas出力の場合、drawImage()非同期処理をlayer合成順に列挙する ・layerをclear ・完了後、同layerにtransformを適用(withBackground=1の場合) ・完了後、同layerにbackground-layerを合成(source-over) ・完了後、同layerにtransformを適用(withBackground=0の場合) ・完了後、同layerにgrid-layerを合成(canvas-globalCompositeOperationを適用) ・完了後、同layerにplot-layerを合成(canvas-globalCompositeOperationを適用) ・完了後、同layerのpost最終処理に移行(source-over) 留意事項を列挙する ・svg出力の場合、canvas-globalCompositeOperation無効(source-over) |
|
目次
post 最終処理順 |
post最終処理順と付随する留意事項について記述する
layer合成後、putImageData()同期出力のpost最終処理を処理順に列挙する ・blur ・filter ・tile ・cut 留意事項を列挙する ・putImageData()同期出力の場合、canvas-globalCompositeOperation無効(source-over) |
|
目次
plot-config |
plot-configについて記述する
plot-configの設定項目を列挙する ・Ver.2.43.20以降、Multi-thread実行時の同時並列数Nthreadを選択可 通常、memory sizeが問題にならない場合、最適なNthread=CPU-core数*(1~2) Ver.2.325.78以降、並列処理の最適なNthread既定値を自動選択 ・Ver.2.136.35以降、描画canvasのcanvas-size(canvas-width,canvas-height=16~2560)をpx数値で入力可 ・bg-image-fileは任意size背景画像fileをread可(Internet Explorer非対応) MIME-type:image read-cancel||image-file以外を選択||canvas-size変更で背景reset svg出力は背景image-file無効 ・背景色はbg-colorの入力値優先で省略時、canvas-backgroundの選択値 背景画像file未指定時のみ有効 ・bg-colorを入力可 ・grid-line-colorを入力可 ・grid-line-widthを選択可 ・marker-sizeを選択可 ・marker-line-widthを選択可 ・plot-line-widthを選択可 ・font-sizeを選択可 axis-values/legend-stringのfont-sizeは選択値 graph-title/axis-labels/originのfont-sizeは選択値+2px ・各軸のgrid分割数grid-x-Ni/grid-y-Njを選択可 ・余白の調整係数kx-adjを選択可 ・marker-colorsを選択可 Ver.2.134.35以降、rainbow/red-blue/red-greenの選択肢を追加 Ver.2.744.110以降、選択肢を24個追加(gradationのformatに準拠) ・Ver.0:旧red-green ・Ver.1:旧red-blue ・rainbow:変更なし Ver.2.744.110以降、内部optionに対応 index.html?marker-colors=red:green:blue:rgb(0,255,255):rgba(255,255,0,0.5) ・legendのx位置を調整するlegend-kxを選択可 ・legendのy位置を調整するlegend-kyを選択可 ・各layerの合成方法canvas-globalCompositeOperationLayerを選択可 ・各layerの背景への合成方法canvas-globalCompositeOperationを選択可 |
|
目次
csv-read |
csv-read機能について記述する
Ver.2.158.38以降、実数値のcsv-fileのread機能を追加(後者typeは実機online-testで特定) ・MIME-type:text/csv || text/comma-separated-values ・Ver.2.848.156以降、論理値literalに対応 ・Ver.2.852.158以降、最長列と空行に対応(空の場合、NaN) 仕様を列挙する ・csv-fileの行と列を転置して予約変数csv連番に代入 ・read範囲の対象外:1行目(header行の前提) ・read範囲の列数:2行目の列数 ・read範囲の行数:2行目~最終行 ・要素が空の場合、 ・要素が実数値以外の場合、NaNに変換 test caseを示す ・csv-file xt, yt, log 0, 0 1, 2, 3 s, 4 5, 6 7, 8 9 ・read実行確定 csv0 -> (0,1,NaN,5,7,9:0,2,4,6,8 ・1列目 csv0[0] -> (0,1,NaN,5,7,9) ・2列目 csv0[1] -> (0,2,4,6,8 ・Ver.2.159.38以降、isNaN関数を追加 (isNaN(trans(csv0[0])),isNaN(trans(csv0[1])))==true -> ( 0,0: 0,0: 1,0: 0,0: 0,0: 0 ) ・MIME-type不一致の場合、error終了 -> input-file.csv not found ・Ver.2.161.38以降、read完了時のlog表示を追加 -> finished reading csv0 MIME-typeを確認する場合、file Checker参照 |
|
目次
strict-mode equation-list |
strict-mode equation-listについて記述する
各buttonはtext入力欄の選択位置にstrict-modeで記述した式変数を挿入する 詳細はstrict-mode式変数list参照 |
|
目次
calc-config |
calc-configについて記述する
各checkboxの詳細は外部option参照 |
|
目次
log-stamp 仕様 |
log-stamp仕様について記述する
svg||csv||history-txt出力時に記録するlog-stampの情報を列挙する ・Repository VERSION ・time-stamp new Date() ・Ver.2.38.18以降、browser識別情報 window.navigator.userAgent |
|
目次
log 表示仕様 |
log表示上の仕様と付随する留意事項について記述する
代入を伴わない場合 ・演算後の値のみ表示する ・直前の実行文の演算結果を保持する予約変数ansへの代入を明示しない 3*2 -> 6 ans -> 6 (3*2,1) -> (6,1) ans -> (6,1) 変数への代入の場合 ・変数名と代入値を明示する x=3*2 -> x=6 x=(3*2,3) -> x=(6,3) 行列要素pattern matchingによる変数への代入の場合 ・変数名のみ明示する ($a,$b)=(1,2) -> stored_var(a) stored_var(b) 式変数への式代入の場合 ・式変数名のみ明示する eqn_x=<(a*x+b=0) -> stored_eqn(eqn_x) eqn_t=<sin(omega(t)) -> stored_eqn(eqn_t) 代入の場合、予約変数ansは更新されない 3*2 -> 6 ans -> 6 x=2; ($a,$b)=(1,2); eqn_x=<(a*x+b=0) -> stored_eqn(eqn_x) ans -> 6 Ver.2.151.38以降、実部の-0表示に対応 -0 -> -0 (-0) -> -0 表示仕様ではないが、以下の演算都合上の仕様について記述する ・代入を括弧で括った場合、0を返す (x=3) || (3=3) -> 0 ・代入後は0が残ると仮定して演算する 2(x=3) || 2(3=3) || 2(=3-3) || 2(0) -> 0 ・代入をcomma,||colon:で区切った場合、0を返す max(x=3,-1,-2) || max(0,-1,-2) -> 0 (1,2:3,4:x=5,x) -> (1,2:3,4:0,5) ・ただし、行列を代入しても次元は残らない (x=(1,2:3,4)) -> 0 詳細は特殊仕様参照 |
|
目次
error-log |
error-logについて記述する
Ver.2.409.86以降、一部のerror-log表示を改善 ・Ver.2.411.87以降、RangeError-log表示の更新不備を修正 ・中置2項演算子 1+ -> (1,1)+ -> **(1,1:) -> &&&(1,1:) -> &&|| -> ・未解決ans 1x -> x(1,1) -> Ver.2.433.90以降、追加修正 x(=<a) -> [MyErr]Invalid ans(x, ・Ver.2.421.88以降、行代入のerror-indexを追加表示 A=(1,2:3,4); A[0]=A -> [MyErr]Invalid store array[0] A=(1,2:3,4); A[0]=1 -> [MyErr]Invalid store size of array[0] ・Ver.2.421.88以降、列代入のerror-indexを追加表示 A=(1,2:3,4); A[][0]=A -> [MyErr]Invalid store array[][0] A=(1,2:3,4); A[][0]=1 -> [MyErr]Invalid store size of array[][0] ・Ver.2.421.88以降、要素代入のerror-indexを追加表示 A=(1,2:3,4); A[0][0]=A -> [MyErr]Invalid store array[0][0] |
|
目次
debugger |
debuggerについて記述する
Ver.2.224.50以降、catched error@operation段階の簡易debuggerを追加 ・該当の実行元j-th sentence終端位置;にcaretを移動(実行確定~catched間に変更の場合、不正確) ・log表示に@j=?を追加 ・Ver.2.274.65以降、catched error@parse段階のpost処理に対応 log表示に@post@j=?を追加 ・Ver.2.278.65以降、catched error@parse段階のpre処理に対応 log表示に@pre@j=?を追加 ・Ver.2.837.143~2.837.144以降、区切り文字を含むcomment文に対応(caret移動の改善) caret移動先の区切り文字の対策:なし ⇒ あり(comment文を文字数分の改行文字\nに置換) clear;1;2//;; 2/**//*;; ;;/*/;;/*/;;*/;;3; ;4;x;6; clear; 1; 2//;; 2/**/ /*;; ;; /*/;; /*/ */ /*;; /*//*/ ;; */;;3; ; 4;x;6; |
|
目次
call stack |
browser由来のcall stackについて記述する
内部的な関数callのnesting深さを制限する最大stack size Maximum call stack size=O(1e4~1e6) size超過error Maximum call stack size exceeded size超過の対策候補を列挙する ・Single-thread実行(並列のstack消費を回避) ・設定で一時的に最大sizeを拡張||size最大のFirefoxで実行 ・漸化式の手動最適化(再帰call ⇒ 再帰高階関数) ・構文の見直し(switch高階関数 ⇒ 論理演算子(短絡評価)) |
|
目次
strict-mode |
strict-modeについて記述する
strict-modeは演算内容の入力規則に以下3点の制約条件を追加する ・乗算記号*省略不可 omitted multiplication sign(*) disabled ・式読出し記号=>省略不可 omitted equation's call sign(=>) disabled ・Ver.2.174.42以降、式変数のarguments省略不可 omitted equation's arguments disabled omitted Pass-by-Equation's bracket({}) disabled ・Ver.2.275.65以降、既定で式変数のcall記号省略不可(syntaxの曖昧さを低減) call記号:=> ⇔ 関数callの丸括弧() _r((n)=<run,run(n,n)=<n+1,3) -> _r(()=<run,run(n,n)=<n+1,3) -> [MyErr]Invalid RX(=<args.length<=1) _r(=<run,run()=<1,3) -> 1 _r((n)=<run(),run=<1,3) -> 1 _r(()=<run,run(n)=<n+1,3) -> 3 _r((n)=<run(n)=>,run(n)=<n+1,3) -> 3 記号省略:自動実行 ⇒ 式変数宣言@Non-strict-modeの判別(callの場合、記号を明示) last{set_x=<(x=1),x=0,set_x,x} -> last{set_x=<(x=1),x=0,set_x(),x} -> 1 ・Ver.2.277.65以降、式変数宣言:BTeのlog表示 clear; set_x=<(x=1),x=0,set_x,x -> (0,0,BTe,0) ・Ver.2.276.65以降、式変数のargumentsの動的判別@Non-strict-modeに対応 定義元:記号=<を省略不可 ⇒ 省略可 call先:省略可(遅延評価の明示を除く) h(x)=<x; f(g)=<g(3); f(h) -> A=(1,2:3,4); f(A)=<A; f(A) -> [MyErr]Invalid args.length=1(f) ・Ver.2.277.65以降、equal記号=の動的判別(記号=<の有無のみ)に対応 f=(x)=<x; f(3)=> -> 3 A={(x)=<x,(x)=<-x,(x)=<x*x} -> (BTe:BTe:BTe) f=A[0] -> stored_eqn(f) f(3) -> 3 ・無名callの末尾return (A)(2)=> -> 4 ・Ver.2.285.67以降、行列要素がBTe単体の場合、iterableの丸括弧()を明示 x=(=<2) -> x= (x)=> -> 2 x=()=<2 -> stored_eqn(x) x() -> 2 ・curried(pipelineの各引数は初回callでclosed) clear; div=(x,y)=<x/y; div_curried_closed_1st_call=(x)=<[(y)=<div(x,y)]; f=div_curried_closed_1st_call; g=div_curried_closed_1st_call; ・無名callのcall記号=>省略不可 (f(2))(1)=>,(f(3))(1)=>,(g(3))(1)=> -> (2,2,2) ・同義(pipe表記) div_curried_closed_1st_call=(x)=<[(x)=<(y)=<div(x,y)](x)=>; ・部分適用 inv_y_applied_partially=div_curried_closed_1st_call(1); (1,5,10).map((x)=<inv_y_applied_partially(x)) -> (1,0.2,0.1) ・pipe f=(x)=<[(y)=<(z)=<(x,y,z)]; xy_z=(f(1))(2)=>; xy_z(3):xy_z(4):xy_z(5) -> (1,2,3:1,2,4:1,2,5) 曖昧さを回避することで演算内容の入力上、引いては演算上の間違いを低減する ・式変数のargumentsを使用して一例を示す ・Non-strict-modeの場合 clear; times(a,b)=<a(b); times(-2) -> [MyErr]Invalid args.length=2(times) clear; times(a,b)=<a(b); times(-2)=> -> [MyErr]Invalid args.length=2(times) clear; times(a,b)=<a(b); times(-2,3) -> -6 clear; times(a,b)=<a(b); times(-2,3)=> -> -6 clear; a(b)=<-999; times(a,b)=<a(b); times(-2,3)=> -> -6 clear; a(b)=<-999; times(a,b)=<a(b)=>; times(-2,3)=> -> -999 clear; times(a,b)=<a*b; times(-2,3) -> -6 clear; times(a,b)=<a*b; times(-2,3)=> -> -6 clear; times(a,b)=<a*b; times=2; times(-2,3)=> -> -6 clear; times(a,b)=<a*b; times=2; times(-2,3) -> (-4,6) ・Ver.2.203.46以降、変数への式読出しの仕様を廃止して式変数への式読出しを追加 clear; times(a,b)=<a*b; times=2; times(-2,3)=>times; times -> clear; times(a,b)=<a*b; times=2; times(-2,3)=>(times) -> -12 clear; times(a,b)=<a*b; a=2; b=3; times -> [MyErr]Invalid null=> clear; times(a,b)=<a*b; a=2; b=3; times=> -> 6 ・Ver.2.253.59以降、引数省略callの仕様廃止(式変数のargumentsの判別を厳格化) ・Ver.2.195.45以降、無名call clear; a=2; [(x)=<a]()=> -> 2 ・Ver.2.275.65以降、既定で式変数のcall記号省略不可 clear; set_x=<(x=1),x=0,set_x,x -> [MyErr]Invalid BTe([object Object]) ・Ver.2.277.65以降、式変数宣言:BTeのlog表示 clear; set_x=<(x=1),x=0,set_x,x -> (0,0,BTe,0) ・Ver.2.277.65以降、変数名symbol単体の場合、動的判別@Non-strict-modeに対応 ・Ver.2.285.67以降、行列要素がBTe単体の場合、iterableの丸括弧()を明示 clear; last{f(x)=<x,f} -> clear; ((x)=<x) -> clear; f=<x; g=f -> stored_eqn(g) ・式変数宣言単体の場合、error終了(予約変数ansへの代入不可) clear; (x)=<x -> [MyErr]Invalid BTe([object Object]) ・Ver.2.279.65以降、iterator演算子の第1引数の動的判別(記号=<の有無のみ)@Non-strict-modeに対応 clear; [(x)=<x,(x)=<-x,(x)=<x*x].map((f)=<f(3)) -> (3,-3,9) ・Ver.2.282.66以降、式変数のargumentsの判別対象を拡張 clear; A_lazy=((x)=<x); f(A)=<(A[0][0])(2)=>; f(=<A_lazy)=> -> ・strict-modeの場合 clear; times(a,b)=<a(b); times(-2) -> [MyErr]Invalid ans isFound clear; times(a,b)=<a(b); times(-2)=> -> [MyErr]Invalid args.length=2(times) clear; times(a,b)=<a(b); times(-2,3) -> [MyErr]Invalid ans isFound clear; times(a,b)=<a(b); times(-2,3)=> -> [MyErr]Invalid operation clear; a(b)=<-999; times(a,b)=<a(b); times(-2,3)=> -> [MyErr]Invalid operation clear; a(b)=<-999; times(a,b)=<a(b)=>; times(-2,3)=> -> -999 clear; times(a,b)=<a*b; times(-2,3) -> [MyErr]Invalid ans isFound clear; times(a,b)=<a*b; times(-2,3)=> -> -6 clear; times(a,b)=<a*b; times=2; times(-2,3)=> -> -6 clear; times(a,b)=<a*b; times=2; times(-2,3) -> [MyErr]Invalid ans isFound ・Ver.2.203.46以降、変数への式読出しの仕様を廃止して式変数への式読出しを追加 clear; times(a,b)=<a*b; times=2; times(-2,3)=>times; times -> clear; times(a,b)=<a*b; times=2; times(-2,3)=>(times) -> [MyErr]Invalid ans isFound clear; times(a,b)=<a*b; a=2; b=3; times -> [MyErr]Invalid REv(times) clear; times(a,b)=<a*b; a=2; b=3; times=> -> [MyErr]Invalid args.length=2(times) ・Ver.2.253.59以降、引数省略callの仕様廃止(式変数のargumentsの判別を厳格化) clear; a=2; f(x)=<a; f=> -> [MyErr]Invalid args.length=1(f) ・Ver.2.195.45以降、無名call clear; a=2; [(x)=<a]()=> -> [MyErr]Invalid args.length=1(null) ・Ver.2.275.65以降、既定で式変数のcall記号省略不可 clear; set_x=<(x=1),x=0,set_x,x -> [MyErr]Invalid REv(set_x) ・Ver.2.280.66以降、plot仕様変更により、未定義の変数を検知不能の致命的な不具合を修正 clear; set_x=<(x=1),x=0,set_x,x -> [MyErr]Undef var(set_x) ・Ver.2.277.65以降、変数名symbol単体の場合、動的判別@Non-strict-modeに対応 clear; last{f(x)=<x,f} -> [MyErr]Undef var(f) clear; f=<x; g=f -> [MyErr]Invalid REv(f) ・Ver.2.277.65以降、式変数宣言:BTeのlog表示 ・Ver.2.285.67以降、行列要素がBTe単体の場合、iterableの丸括弧()を明示 clear; ((x)=<x) -> ・式変数宣言単体の場合、error終了(予約変数ansへの代入不可) clear; (x)=<x -> [MyErr]Invalid BTe([object Object]) ・Ver.2.279.65以降、iterator演算子の第1引数の動的判別(記号=<の有無のみ)@Non-strict-modeに対応 clear; [(x)=<x,(x)=<-x,(x)=<x*x].map((f)=<f(3)) -> [MyErr]Invalid URh-args.f ・Ver.2.282.66以降、式変数のargumentsの判別対象を拡張 clear; A_lazy=((x)=<x); f(A)=<(A[0][0])(2)=>; f(=<A_lazy)=> -> |
|
目次
内部option |
UIには表示しない内部optionについて記述する
browser上部のURL入力欄のGET入力で内部optionを変更可(UI設定値||既定値を上書き可) ・html直後の?に続けて&区切りでparameterを渡す index.html?param0=value0¶m1=value1¶m2=value2&... Ver.2.184.44以降、real自動切替機能を使用する場合、-1を設定 useComplex=-1 strict-modeで実行する場合、false||0以外を設定 useStrict=true useStrict=1 情報落ちの発生や微分・積分の数値誤差を評価しない場合、falseを設定 checkError=false ・演算量が数倍軽くなる ・Ver.2.84.32以降、さらに行列操作を最適化する場合、0を設定 checkError=0 ・欠損要素を含む行列操作の予期せぬerror終了を許容する (1,2:3)[0][0][][] -> Cannot read properties of undefined ・Ver.2.84.32以降、数値誤差を評価して行列操作のみを最適化する場合、負数を設定 checkError=-1 Ver.2.31.17以降、useScopeを追加 useScope=false:完全な後方互換で変数のscopeを一切使用しない useScope=true:すべての括弧に変数のscopeを使用する(多重積分等、参照透過性の支障あり) useScope=BT2:波括弧{}のみ変数のscopeを使用する useScope=BT1:丸括弧()のみ変数のscopeを使用する Ver.2.32.17以降、以下の条件を追加 useScope=notBT2:波括弧{}以外で変数のscopeを使用する useScope=notBT1:丸括弧()以外で変数のscopeを使用する useScope=notBT0:角括弧[]以外で変数のscopeを使用する useScope=default(上記以外):角括弧[]のみ変数のscopeを使用する Ver.2.213.47以降、useScopeWithを追加 useScopeWith=false||0:追加なし useScopeWith=SEe:式代入記号=<に変数のscopeを追加(function-scope) useScopeWith=BTe(上記以外):式変数のarguments付の式代入記号=<に変数のscopeを追加 Ver.2.221.50以降、useFuncを追加 useFunc=1:すべて小文字 useFunc=2:すべて大文字 useFunc=3:最初のみ大文字 useFunc=0(上記以外):大文字・小文字を区別しない Ver.2.249.57以降、use$letを追加 use$let=false||0:$const use$let=true(上記以外):$let Ver.2.250.57以降、useMutexを追加 useMutex=false||0:mutex対象の宣言を禁止しない useMutex=true(上記以外):mutex対象の宣言を禁止する 演算子のprecedenceを変更する場合 ・演算子のtag名を優先順にcomma,区切りで列挙する ・Ver.2.59.26以降、論理演算子を追加 ・Ver.2.71.28以降、bit not演算子を追加 ・Ver.2.81.32以降、論理NOT演算子を追加 ・Ver.2.87.32以降、一部の演算子をPythonに準拠 ・Ver.2.168.41以降、論理XOR演算子を追加 ・Ver.2.192.44以降、dot演算子を追加(URi,URfをURに統合) ・Ver.2.752.113以降、前置単項演算子(PU)のsize演算子を追加 precedence= UR,PU,BRpp,BRp,BRmo,BRdm,BRsa, PUbn,BRbs,BRba,BRbx,BRbo,BRcn,BRrl,PUlN,BRlA,BRlX,BRlO ・別途、乗算記号*の省略を許容しない場合、tag名BRmoを削除する その場合、treeを全走査判定する無駄な演算量が減る Ver.2.207.46以降、testを追加 test=true:calc-configに内部optionのuseScope||precedenceを追加表示 |
|
目次
外部option |
外部optionの設定項目を列挙する
・O(error) Ver.2.166.40以降、追加 ・2項演算子のassociativity ・記号省略乗算 ・comma演算子 ・use$let Ver.2.249.57以降、追加 ・useMutex Ver.2.250.57以降、追加 ・useFunc Ver.2.221.50以降、追加 ・useScopeWith Ver.2.213.47以降、追加 ・Multi-thread実行 |
|
目次
O(error) |
外部optionのO(error)と付随する留意事項について記述する
Ver.2.166.40以降、情報落ちと数値誤差のlog表示||非表示を選択可 ・内部optionのcheckError=true||false |
|
目次
2項演算子の associativity |
外部optionの2項演算子のassociativityと付随する留意事項について記述する
2項演算子のassociativityを選択可 ・左から順に結合する場合、左結合(以降、Left-AssociativityをLAと省略する) ・右から順に結合する場合、右結合(以降、Right-AssociativityをRAと省略する) unchecked既定:左結合 +3-5+7-9 || ((((0+3)-5)+7)-9) -> -4 (1,2)-(3,4)-(5,6) || (((1,2)-(3,4))-(5,6)) -> (-7,-8) -(1,1)-(2,2) || (((0,0)-(1,1))-(2,2)) -> (-3,-3) (1,2){3,4}(5,6) || (((1,2){3,4})(5,6)) || 11(5,6) -> (55,66) checked選択:右結合 +3-5+7-9 || (0+(3-(5+(7-9)))) -> 0 (1,2)-(3,4)-(5,6) || ((1,2)-((3,4)-(5,6))) -> (3,4) -(1,1)-(2,2) || ((0,0)-((1,1)-(2,2))) -> (1,1) (1,2){3,4}(5,6) || ((1,2)({3,4}(5,6))) || (1,2)(15,18:20,24) -> (55,66) 留意事項を列挙する ・前置単項演算子の符号は同種の中置2項演算子と区別しない ・符号の左側には0||zeros行列が存在すると仮定して結合する 詳細は特殊仕様参照 |
|
目次
記号省略乗算 |
外部optionの記号省略乗算と付随する留意事項について記述する
記号省略乗算と除算の演算子のprecedenceを切替え可 unchecked既定:除算より記号省略乗算優先 1/2(2) || 1/(2(2)) -> 0.25 checked選択:記号省略乗算より除算優先 1/2(2) || (1/2)(2) -> 1 記号省略乗算を許容しない場合、内部option参照 |
|
目次
comma 演算子 |
外部optionのcomma演算子と付随する留意事項について記述する
Ver.2.74.29以降、拡張行列演算におけるcomma演算子の使用を選択可 ・Ver.2.88.32以降、定義できない乗算||減算||加算を拡張行列演算に追加 comma演算子は行vectorの最終要素を取り出す unchecked既定:comma演算子未使用 (1,2:3,4)i -> (i,2i:3i,4i) (1,2:3,4)(i) || (1,2:3,4)*i -> (i,2i:3i,4i) checked選択:comma演算子使用 (1,2:3,4)i || ((1,2)i:(3,4)i) -> (2i:4i) (1,2:3,4)(i) || (1,2:3,4)*i -> (2i:4i) 留意事項を列挙する ・無次元の演算の場合、comma演算子は常に有効 |
|
目次
use$let |
外部optionのuse$letと付随する留意事項について記述する
Ver.2.249.57以降、再代入と重複宣言を禁止するconst宣言の既定値を選択可 ・Ver.2.254.59以降、$let宣言の再代入の仕様変更(初回のみ、$あり ⇒ 常時、$あり) unchecked既定:$const宣言 $なし:let宣言 $あり:const宣言 checked選択:$let宣言 $なし:const宣言 $あり:let宣言 留意事項を列挙する ・明示的な代入のみ対応 ・非対応の機能(後方互換のlet宣言)を列挙する ・行列要素pattern matching ・式変数のarguments(厳密にはscope不定) ・高階関数||高階行列関数のdummy変数(scope変数の宣言と干渉あり仕様) ・Ver.2.261.61以降、define判別idを追加して式変数のre-callに対応(再利用の場合、id削除) [$f=<0,$a=1,$b=2,=<(c)=<f=>+a+b+c]=>f,f(3)=>,f(4)=>,f(5)=> -> (0,6,7,8) ・式変数の場合、re-call毎に判別するため、無名callのclosureより重い f(c)=<[$f=<0,$a=1,$b=2,=<f=>+a+b+c]=>,f(3)=>,f(4)=>,f(5)=> -> ・Ver.2.262.61以降、式変数への式読出しに対応 [$f=<0,$a=1,$b=2,=<(c)=<f=>+a+b+c]=>$g,g=<1 -> [MyErr]Invalid SEe-scope-const(g) f(c)=<[$f=<0,$a=1,$b=2,=<f=>+a+b+c]=>$f,f(3)=> -> [MyErr]Invalid SEe-scope-existed(f) ・Ver.2.262.62以降、define判別idが消失する致命的な不具合を修正(value-id ⇒ name-id継承) clear; $a=-1; ((((a)=<(b)=<(a,b))|||false)(1)=>)(2)=> -> ・Ver.2.264.62以降、式変数の再利用に対応(id削除 ⇒ name-id保持) clear -> local storage cleared $x=-1; x -> -1 f(x)=<x; f(1)=> -> f(x)=<[=<x]=>; f(1)=> -> 1 clear -> local storage cleared $f=<-1; f=> -> -1 f(x)=<[=<x]=>; f(1)=> -> g(=<f)=<f=>; g(=<1)=> -> g(=<f)=<[=<f=>]=>; g(=<1)=> -> 1 |
|
目次
useMutex |
外部optionのuseMutexと付随する留意事項について記述する
Ver.2.250.57以降、mutex対象の宣言禁止を選択可 ・Ver.2.291.71以降、排他処理の仕様変更 同時宣言:error終了 ⇒ 他方を削除 mutex対象:変数・式変数の同一変数名symbolのscope変数を同時宣言 unchecked既定:mutex対象の宣言を禁止しない clear; f=<2,f=1,f,f=> -> (0,0,1,2) clear; f=1,f=<2,f,f=> -> (0,0,1,2) clear; f=1,[f=<2,f,f=>] -> (0,0,1,2) clear; [f=1,f=<2,f,f=>] -> (0,0,1,2) clear; [f=1,[f=<2,f,f=>]] -> (0,0,1,2) checked選択:mutex対象の宣言を禁止する ・Ver.2.291.71以降、排他処理の他方を削除 clear; f=<2,f=1,f,f=> -> clear; f=1,f=<2,f/*Non-strict-mode*/,f=> -> clear; f=1,[f=<2,f,f=>] -> (0,0,1,2) clear; [f=1,f=<2,f/*Non-strict-mode*/,f=>] -> clear; [f=1,[f=<2,f,f=>]] -> (0,0,1,2) |
|
目次
useFunc |
外部optionのuseFuncと付随する留意事項について記述する
Ver.2.221.50以降、名前衝突緩和のため、実装関数名の大文字・小文字のformatを選択可 ・Ver.2.382.86以降、_?dummy変数の高階関数||高階行列関数に対応(?部分の1文字が対象) ・Ver.2.390.86以降、命令文とmethod演算子以外の全予約語に対応(定数・虚数単位iを含む) FuNc既定:大文字・小文字を区別しない func選択:すべて小文字 FUNC選択:すべて大文字 Func選択:最初のみ大文字 留意事項を列挙する ・定数は ・_?dummy変数の高階関数||高階行列関数は ・browserの入力欄で大文字の虚数単位Iと小文字のlを判別困難 |
|
目次
useScope With |
外部optionのuseScopeWithと付随する留意事項について記述する
Ver.2.213.47以降、変数のscopeの追加を選択可 ・Ver.2.213.48以降、useScopeを含む選択切替の不具合を修正 ・Ver.2.213.48以降、式変数の再利用に未配慮の変更取消し ・Ver.2.228.56以降、追加選択時にscope継承が常に有効の致命的な不具合を修正 =<選択:B=-1,g=<B,[B=10,[B=20,[B=30,=<g]=>f,=<f]=>f,=<f]=>f,f=>,f==> -> (0,0,0, =<選択:B=-1,g=<B,[B=10,[B=20,[B=30,=<g]=>f,=<f]=>f,==<f]=>f,f=>,f==> -> (0,0,0,10,-1) =<選択:B=-1,g=<B,[B=10,[B=20,[B=30,==<g]=>f,=<f]=>f,==<f]=>f,f=>,f==> -> (0,0,0,10,-1) =<選択:B=-1,g=<B,[B=10,[B=20,[B=30,==<g]=>f,=<f]=>f,=<f]=>f,f=>,f==> -> (0,0,0,30,-1) false既定:追加なし =<選択:式代入記号=<に変数のscopeを追加(function-scope) (args)=<選択:式変数のarguments付の式代入記号=<に変数のscopeを追加 test caseを列挙する clear; x=1,((x)=<x)(3)=>,x -> (0,3,1) clear; x=1,((x)=<x)(3)=>f,f=>,x -> (0,0,3,1) clear; x=1,[(x)=<=<x/*not-resolved*/](3)=>f,f=>,x -> (0,0,3,1) 既定時 clear; x=1,((x)=<=<x)(3)=>f,f=>,x -> (0,0,1,1) 選択時 clear; x=1,((x)=<=<x)(3)=>f,f=>,x -> (0,0,3,1) 留意事項を列挙する ・追加を選択の場合、strict-mode式変数list等、要修正 ・単独scopeの角括弧[] ⇒ () ・式変数のscope継承callの式読出し記号==>を明示 ・追加を選択の場合、支障あり(pollution disabled) 既定時 [arr=[],_s((n)=<arr=(arr,n),1,3),=<arr]=> -> (1,2,3) 既定時 [arr=[],_s((n)=<[,arr=(arr,n)],1,3),=<arr]=> -> [] =<選択時 [arr=[],_s((n)=<arr=(arr,n),1,3),=<arr]=> -> [] (args)=<選択時 [arr=[],_s((n)=<arr=(arr,n),1,3),=<arr]=> -> [] (args)=<選択時 [arr=[],_sn(=<arr=(arr,n),1,3),=<arr]=> -> (1,2,3) ・同義 [arr=_r(=<[hass(arr)==0&&&(arr=[],n=0),n=n+1,arr=(arr,n),=<arr]=>,,3),=<arr]=> -> (1,2,3) ・式変数の再利用の場合、保存時のflagを継承 |
|
目次
Multi-thread 実行 |
外部optionのMulti-thread実行と付随する留意事項について記述する
Multi-thread実行を選択可 checked既定:Multi-thread実行(演算を中断可) unchecked選択:Single-thread実行(演算を中断不可) 留意事項を列挙する ・Single-thread実行の場合、browser既定のtimeoutまで演算||処理を中断不可 ・Graphing Calculatorの場合、Single-thread実行の演算||処理を列挙する ・t0/t1の演算 ・post処理を含むcanvas描画処理 |
|
目次
演算子 の大分類 |
演算子の大分類と付随する留意事項について記述する
主要な演算子の大分類/記法を列挙する ・後置単項演算子 left-operand operator ・前置単項演算子 operator right-operand ・中置2項演算子 left-operand operator right-operand ・中置3項演算子の一例(条件演算子) left-operand-boolean operator1 right-operand1 operator2 right-operand2 小分類は演算子のprecedence参照 |
|
目次
2項演算子の associativity |
2項演算子のassociativityと付随する留意事項について記述するについて記述する
Left-Associativity(左結合) +3-5+7-9 || ((((0+3)-5)+7)-9) -> -4 (1,2)-(3,4)-(5,6) || (((1,2)-(3,4))-(5,6)) -> (-7,-8) -(1,1)-(2,2) || (((0,0)-(1,1))-(2,2)) -> (-3,-3) (1,2){3,4}(5,6) || (((1,2){3,4})(5,6)) || 11(5,6) -> (55,66) ・Excel準拠の^演算子は左結合既定 3^2^3 || ((3^2)^3) -> 729 ・Ver.2.87.32以降、**演算子は右結合固定に変更 3**2**3 || (3**(2**3)) -> 6561 ・Ver.2.87.32以降、**演算子は^演算子より優先 3**2^3 || ((3**2)^3) -> 729 3^2**3 || (3^(2**3)) -> 6561 Right-Associativity(右結合) +3-5+7-9 || (0+(3-(5+(7-9)))) -> 0 (1,2)-(3,4)-(5,6) || ((1,2)-((3,4)-(5,6))) -> (3,4) -(1,1)-(2,2) || ((0,0)-((1,1)-(2,2))) -> (1,1) (1,2){3,4}(5,6) || ((1,2)({3,4}(5,6))) || (1,2)(15,18:20,24) -> (55,66) 3^2^3 || (3^(2^3)) -> 6561 3**2**3 || (3**(2**3)) -> 6561 3**2^3 || ((3**2)^3) -> 729 3^2**3 || (3^(2**3)) -> 6561 2**2**2**2 || (2**(2**(2**2))) -> 65536 留意事項を列挙する ・中置2項演算子を短絡評価する場合、論理演算子参照 中置2項演算子のassociativityを選択する場合、外部option参照 |
|
目次
演算の precedence |
演算のprecedenceと付随する留意事項について記述する
演算のprecedenceに従って実行文を解釈し、順番に演算を実行する 主要なprecedenceを優先順に列挙する ・区切り文字 ・式変数への式代入 遅延評価保証のため、左結合 ・論理演算子(短絡評価) 先読みで結合 ・最上位関数 ・括弧 ・式読出し(call記号=>明示) ・変数読出し||method演算子 ||式読出し(call記号=>省略)@Non-strict-mode ・関数 ・演算子 ・変数への代入 これに従う演算結果の一例を示す max(x=1,(x):2,3)[0]2 || (max((0,1:2,3)[0]))2 || (max(0,1))2 || (1)2 -> 2 留意事項を列挙する ・演算のprecedenceは言語仕様によって異なる 詳細は内部仕様参照 |
|
目次
method 演算子 |
scope変数を直接editするmethod演算子と付随する留意事項について記述する
Ver.2.298.72以降、変数のprototype method代替のunshift/push/shift/pop()を追加 ・Ver.2.301.73以降、致命的な不具合を修正(const宣言の変数の操作不可) const宣言:参照 ⇒ 行列iterable clear; $A=1; A.pop(); A -> clear; $A=(1,2:3,4); A.push(5); A -> ・Ver.2.372.86以降、flip()を追加(in-placeのreverse処理) ・Ver.2.829.139以降、unshift/push()を拡張(行列結合より高速) 第1引数:行vector ⇒ 行列 ・Ver.2.830.139以降、unshift/push()の遅延評価を廃止 引数の遅延評価:あり ⇒ なし(式渡しの判別) .unshift()演算子 ・直接editの場合、NaNを返す clear; A=(1,2:3,4); A.unshift(5) -> NaN clear; A=(1,2:3,4); A.unshift(5); A -> (5,1,2:3,4) clear; A=(1,2:3,4); A.unshift(=<(5,6)); A -> (5,6,1,2:3,4) ・複数行の操作不可(Ver.2.300.72以降、log表示内容を訂正) clear; A=(1,2:3,4); A.unshift(=<(5:6)); A -> [MyErr]Invalid unshift(sizer(arr)=1) ・行指定の場合、行参照を使用 clear; A=(1,2:3,4); A[1].unshift(5); A -> (1,2:5,3,4) ・行の反転参照 clear; A=(1,2:3,4); A[-1].unshift(=<(5,6)); A -> (1,2:5,6,3,4) ・最初行の追加 clear; A=(1,2:3,4); A[-3].unshift(5); A -> (5:1,2:3,4) ・参照不可の場合、error終了 clear; A=(1,2:3,4); A[2].unshift(5); A -> [MyErr]Invalid reference of array clear; A=(1,2:3,4); A[-4].unshift(5); A -> [MyErr]Invalid reference of array ・列指定不可 clear; A=(1,2:3,4); A[1][1].unshift(5); A -> [MyErr]Invalid unshift(ref.length<=1) ・展開済みiterableの操作不可 clear; (1,2:3.4).unshift(5) -> [MyErr]Invalid ans isFound .shift()演算子 clear; A=(1,2:3,4); A.shift() -> 1 clear; A=(1,2:3,4); A.shift(); A -> (2:3,4) clear; A=(1,2:3,4); A[0].shift() -> 1 clear; A=(1,2:3,4); A[0].shift(); A -> (2:3,4) clear; A=(1,2:3,4); A[1].shift() -> 3 clear; A=(1,2:3,4); A[1].shift(); A -> (1,2:4) ・行要素が空の場合、行数を維持してNaNを返す clear; A=[]; A.shift() -> NaN clear; A=(1:); A.shift(); A.shift(); A -> (:0) clear; A=(1:); A.shift(); A.unshift(2); A -> (2:0) ・展開済みiterableの操作不可 clear; (1,2:3.4).shift() -> [MyErr]Invalid ans isFound ・空括弧のみ有効 clear; A=(1,2:3,4); A.shift -> [MyErr]Invalid shift() clear; A=(1,2:3,4); A.shift(2) -> [MyErr]Invalid shift() .push()演算子 clear; A=(1,2:3,4); A.push(5) -> NaN clear; A=(1,2:3,4); A.push(5); A -> (1,2:3,4,5) clear; A=(1,2:3,4); A.push(=<(5,6)); A -> (1,2:3,4,5,6) clear; A=(1,2:3,4); A[0].push(5); A -> (1,2,5:3,4) ・行の反転参照 clear; A=(1,2:3,4); A[-1].push(=<(5,6)); A -> (1,2:3,4,5,6) ・最終行の追加 clear; A=(1,2:3,4); A[2].push(5); A -> (1,2:3,4:5) ・参照不可の場合、error終了 clear; A=(1,2:3,4); A[3].push(5); A -> [MyErr]Invalid reference of array clear; A=(1,2:3,4); A[-3].push(5); A -> [MyErr]Invalid reference of array .pop()演算子 clear; A=(1,2:3,4); A.pop() -> 4 clear; A=(1,2:3,4); A.pop(); A -> (1,2:3) clear; A=(1,2:3,4); A.pop(5) || A.pop(=<5) -> [MyErr]Invalid pop() clear; A=(1,2:3,4); A[0].pop() -> 2 clear; A=(1,2:3,4); A[0].pop(); A -> (1:3,4) clear; A=(1,2:3,4); A[1].pop() -> 4 clear; A=(1,2:3,4); A[1].pop(); A -> (1,2:3) .flip()演算子 Ver.2.372.86以降、追加 clear; A=(1,2:3,4); A.flip() -> NaN ・全要素の反転 clear; A=(1,2:3,4:i); A.flip(); A -> (i:4,3:2,1) ・欠損要素を自動で埋めない clear; A=(1,2:3); A.flip(); A -> (3:2,1) clear; A=[]; A.flip(); A -> [] clear; A=(1,2:3,4); A.flip(5) || A.flip(=<5) -> [MyErr]Invalid flip() ・行指定の反転 clear; A=(1,2:3,4); A[0].flip(); A -> (2,1:3,4) clear; A=(1,2:3,4); A[1].flip(); A -> (1,2:4,3) clear; A=(1,2:3,4); A[-1].flip(); A -> (1,2:4,3) clear; A=(1,2:3,4); A[2].flip() -> [MyErr]Invalid reference of array test caseを列挙する ・Ver.2.301.73以降、評価順を修正 clear; A.push(=<(A=1,A.push(2))); A -> clear; A[1].push(=<(A=(1,2,3,4),A.unshift(5),A.push(6),=<A)=>); A -> clear; A[1].push(=<[A=(1,2,3,4),A.unshift(5),A.push(6),=<A]=>); A -> [MyErr]Undef var(A.push) ・Ver.2.300.72以降、prop未定義の場合、error終了 1.Test() -> 留意事項を列挙する ・参照を返却する代替としてNaNを返す(shift/popを除く) ・変数読出し同等の演算のprecedence ・宣言の場合、操作後の内容を反映してlog表示(出力用の複製なし) clear; A=(1,2:3,4); A.pop() -> A=(1,2:3); 4 ・pollution disabled clear; A=(1,2:3,4); [,A.push(-1)] -> [MyErr]Undef var(A.push) ・chain不可 |
|
目次
演算子の precedence |
演算子のprecedenceと付随する留意事項について記述する
演算子のprecedenceを優先順に列挙する ・論理演算子(短絡評価) Ver.2.157.38以降、追加 ・中置2項演算子 ・論理ANDs||ORs演算子 &&& || ||| ||ANDss||ORss演算子 &&&& || |||| Ver.2.196.46以降、追加 ・算術演算子 ・後置単項演算子 Ver.2.192.44以降、統合(優先順位なしの左結合) ・dot演算子 . || ' Ver.2.192.44以降、追加 ||iterator演算子 Ver.2.214.49以降、追加 ・前置単項演算子 Ver.2.752.113以降、追加 ・size演算子 # || ## || ### Ver.2.752.113以降、追加 ・中置2項演算子 ・べき乗演算子 ** Ver.2.87.32以降、右結合固定に変更 ・べき乗演算子 ^ Ver.2.87.32以降、**演算子の下位に分離 ・四則演算子 ・記号省略乗算 ・剰余||整数商||除算||乗算演算子 % || %% || / || * Ver.2.87.32以降、整数商を追加 ・減算||加算演算子 - || + ・前置単項演算子 ・減算-||加算+の符号は同種の中置2項演算子と区別しない ・bit演算子 ・前置単項演算子 ・bit not演算子 ~ Ver.2.71.28以降、追加 ・中置2項演算子 ・bit shift演算子 << || >> || >>> ・bit and演算子 & ・bit xor演算子 @ ・bit or演算子 | ・比較演算子 ・中置2項演算子 ・大小比較演算子 < || <= || >= || > ・関係演算子 ・中置2項演算子 ・厳密等価||等価||不等価演算子 === || == || <> Ver.2.167.40以降、追加 ||厳密不等価演算子 <<>> Ver.2.225.52以降、追加 ||行列の厳密等価演算子 ==== Ver.2.847.153以降、追加 ||行列の厳密不等価演算子 <<<>>> Ver.2.847.153以降、追加 ・論理演算子 Ver.2.59.26以降、追加 ・前置単項演算子 ・論理NOT演算子 ~~ Ver.2.81.32以降、追加 ・中置2項演算子 ・論理AND演算子 && ・論理XOR演算子 @@ Ver.2.168.41以降、追加 ・論理OR演算子 || 留意事項を列挙する ・Ver.2.192.44以降、後置単項演算子は優先順位なしの左結合 ・前置単項演算子のbit not||論理NOTは記号共通(~||~~)のため、左結合(連続する場合、括弧を明示) ・演算子のprecedenceは言語仕様によって異なる 演算子のprecedenceを変更する場合、内部option参照 ・Ver.2.157.38以降、追加の論理演算子(短絡評価)を除く |
|
目次
算術演算子 |
算術演算子と付随する留意事項について記述する
減算と加算は区別せず、2項演算子のassociativityに従って演算する LA既定時 +3-5+7-9 || ((((0+3)-5)+7)-9) -> -4 RA選択時 +3-5+7-9 || (0+(3-(5+(7-9)))) -> 0 除算と乗算は区別せず、2項演算子のassociativityに従って演算する LA既定時 1*2/3*4/5 || ((((1*2)/3)*4)/5) -> 0.5333333333333333 RA選択時 1*2/3*4/5 || (1*(2/(3*(4/5)))) -> 0.8333333333333333 Ver.2.87.32以降、剰余・整数商の演算子のprecedenceを除算と乗算に統合する LA既定時 -5%(-4)%%3/2*1 || (0-((((5%(-4))%%3)/2)*1)) -> 0 RA選択時 -5%(-4)%%3/2*1 || (0-(5%((-4)%%(3/(2*1))))) -> -1 記号省略乗算は除算より優先する 記号省略乗算優先既定時 1/2(2) || 1/(2(2)) -> 0.25 除算優先選択時 1/2(2) || (1/2)(2) -> 1 べき乗の中置2項演算子は四則演算子より優先する -2^2 || (0-(2^2)) -> -4 -3**2 || (0-(3**2)) -> -8.999999999999998 後置単項演算子は中置2項演算子より優先する 3^2! || 3^(2!) || 3^(2*1) -> 8.999999999999998 2*3!! || 2*(3!!) || 2*(3*1) -> 6 ・階乗のoperandは0を含む自然数のみ対応 ・Γ(1)=1より、0!=1 0! || 0!! || 0!!! -> 1 !!! || !! || ! || 0! -> 1 3.3!! || 3!! || 3*1 -> 3 (3)!!! || 3!!! || 3 -> 3 -(3)! || (0-(3!)) || (0-(3*2*1)) -> -6 ・階乗のoperandが負の場合、未定義で (-3)! || ((-3)!) -> false (-3)!! || ((-3)!!) -> false (-3)*!! || (-3)*(0!!) -> -3 -3*! || (0-(3*(0!))) -> -3 ・虚数単位iは後置単項演算子とする 1/2i || 1/(2i) -> -0.5i 算術演算子はbit演算子より優先する -0xff>>2 || (-0xff)>>2 || ((0-255)>>2) -> -64 -0xff>>1@1 || (-0xff>>1)@1 || ((0-128)@1) -> -127 記号省略乗算を許容しない場合、内部option参照 |
|
目次
dot演算子 |
dot演算子と付随する留意事項について記述する
Ver.2.192.44以降、転置行列関数を代替するdot演算子を追加 ・後置単項演算子の演算子のprecedenceを統合(左から順次処理) ・Ver.2.214.49以降、dot演算子を拡張してiterator演算子を追加 trans行列関数代替演算子. (1,2i:3,4i:-5i). || trans(1,2i:3,4i:-5i) -> (1,3,-5i:2i,4i,0) A=(1,2i:3,4i:-5i); A. -> (1,3,-5i:2i,4i,0) ・連続転置 A=(1,2i:3,4i:-5i); A.. -> (1,2i:3,4i:-5i,0) ・後置単項演算子は左から順次処理 A=(1,2i:3,4i:-5i); A.i! -> (1,1,120:false,false,1) A=(1,2i:3,4i:-5i); A.!i -> (i,6i,i:i,i,i) A=(1,2i:3,4i:-5i); (A)i!. -> (1,1,120:false,false,0) A=(1,2i:3,4i:-5i); A!i. -> (i,6i,i:i,i,0) ・小数点と判別されない場合 1..2 || (((1).).)2 || 1*2 -> 2 ・null-leftの場合、error終了 ..2 -> [MyErr]Invalid null. ・csv-format判定の場合 .2 || (0.2) -> 0.2 7. || (7.0) -> 7 htrans行列関数代替演算子' (1,2i:3,4i:-5i)' || htrans(1,2i:3,4i:-5i) -> (1,3,5i:-2i,-4i,0) A=(1,2i:3,4i:-5i); A' -> (1,3,5i:-2i,-4i,0) A=(1,2i:3,4i:-5i); A'' -> (1,2i:3,4i:-5i,0) A=(1,2i:3,4i:-5i); A'i! -> (1,1,false:2,24,1) A=(1,2i:3,4i:-5i); A'!i -> (i,6i,i:i,i,i) A=(1,2i:3,4i:-5i); (A)i!' -> (1,1,120:false,false,0) A=(1,2i:3,4i:-5i); A!i' -> (-i,-6i,-i:-i,-i,0) |
|
目次
iterator 演算子 |
iterator演算子と付随する留意事項について記述する
Ver.2.214.49以降、Nativeの高階関数を代替するiterator演算子を追加 ・式変数のarguments付の展開式を式渡し||symbol渡し ・Ver.2.217.50以降、欠損値の場合、NaNを返す 1.filter((x)=<false) -> ・Ver.2.226.56以降、dummy変数がscope変数に残存する不具合を修正 ・Ver.2.257.59以降、iterator対象を拡張 iterator対象:変数 ⇒ 変数・式変数 ・Ver.2.279.65以降、第1引数の動的判別(記号=<の有無のみ)@Non-strict-modeに対応 clear; A=[(x)=<x,(x)=<-x,(x)=<x*x]; A.map((f)=<f(3)) -> (3,-3,9) clear; [(x)=<x,(x)=<-x,(x)=<x*x].map((f)=<f(3)) -> (3,-3,9) .map()演算子 clear; f(x)=<x*2; (1,2:3,4).map(=<f) -> (2,4:6,8) clear; (1,2:3,4).map((x)=<x*2) -> (2,4:6,8) clear; A=(1,2:3,4); A.map((x)=<x*2) -> (2,4:6,8) clear; A=(1,2:3,4); A.map((x,i_,j_,self_cloned)=<self_cloned[i_][j_]*2) -> (2,4:6,8) ・self_clonedは参照非共有 clear; A=(1,2:3,4); A.map((x,i_,j_)=<A[i_][j_]*2) -> (2,4:6,8) .filter()演算子 clear; f(x)=<x>2; (1,2:3,4).filter(=<f) -> (3,4:1,1:0,1) clear; (1,2:3,4).filter((x)=<x>2) -> (3,4:1,1:0,1) clear; A=(1,2:3,4); A.filter((x)=<x>2) -> (3,4:1,1:0,1) clear; A=(1,2:3,4); A.filter((x,i_,j_,self_cloned)=<self_cloned[i_][j_]>2) -> (3,4:1,1:0,1) clear; A=(1,2:3,4); A.filter((x,i_,j_)=<A[i_][j_]>2) -> (3,4:1,1:0,1) clear; A=(1,2:3,4); mat2coo(A)-A.filter((x)=<x) -> (0,0,0,0:1,1,1,1:1,1,1,1) clear; A=(0,2:3,4); mat2coo(A)-A.filter((x)=<x<>0) -> (0,0,0:1,1,1:1,1,1) .filter0()演算子 Ver.2.263.62以降、追加 clear; A=(1,2:3,4); (A.filter((x)=<x>2))[0] || A.filter0((x)=<x>2) -> (3,4) 留意事項を列挙する ・演算子のprecedence:後置単項演算子同等 ・objectのpropertyは未実装 ・引数不正の場合、error終了 clear; (1,2:3,4).map() -> [MyErr]Invalid .map(null) ・引数のarguments省略不可 clear; (1,2:3,4).map(()=<x*2) -> [MyErr]Invalid binary operation clear; x=1; (1,2:3,4).map(()=<x*2) -> [MyErr]Invalid binary operation |
|
目次
size演算子 |
size演算子と付随する留意事項について記述する
Ver.2.752.113以降、size行列関数を代替する前置単項演算子のsize演算子を追加 ・#演算子:sizer(right) ・##演算子:sizec(right) ・###演算子:Nelements(欠損要素以外の要素数) size演算子 #(1,2,3:4,5) -> 2 ##(1,2,3:4,5) -> 3 ###(1,2,3:4,5) -> 5 #(1,2,3:4,5). || #((1,2,3:4,5).) || #trans(1,2,3:4,5) -> 3 A=(1,2,3:4,5); #A,#(1,2,3:4,5),sizer(A),##A,##(1,2,3:4,5),sizec(A),###A -> (2,2,2,3,3,3,5) A=(1,2,3:4,5); #A.,#(1,2,3:4,5).,sizer(A.),##A.,##(1,2,3:4,5).,sizec(A.),###A. -> (3,3,3,2,2,2,6) A=(1,2,3:4,5); #A..,#(1,2,3:4,5)..,sizer(A..),##A..,##(1,2,3:4,5)..,sizec(A..),###A.. -> (2,2,2,3,3,3,6) #1,##2,###3 -> (1,1,1) ####1 -> [MyErr]Invalid #### ## -> [MyErr]Invalid #null ・Ver.2.756.113以降、空行列に対応 ###[],##[],#[],#() -> ・式変数 clear; f=<1; #f -> [MyErr]Invalid #null clear; f=<1; #(f) || size(f) -> 1 留意事項を列挙する ・演算子のprecedence:後置単項演算子の直後 |
|
目次
剰余・ 整数商演算子 |
剰余・整数商演算子と付随する留意事項について記述する
Ver.2.87.32以降、整数商演算子を追加 剰余 3.2%2 -> 1.2000000000000002 -3.2%2 -> -1.2000000000000002 (-3.2)%2 -> -1.2000000000000002 3.2%(-2) -> 1.2000000000000002 -3.2%(-2) -> -1.2000000000000002 (-3.2)%(-2) -> -1.2000000000000002 3.2%1.2 -> 0.8000000000000003 2.2i%1 -> 0 2.2%i -> NaN 整数商 3.2%%2 -> 1 -3.2%%2 -> -1 (-3.2)%%2 -> -1 3.2%%(-2) -> -1 -3.2%%(-2) -> 1 (-3.2)%%(-2) -> 1 3.2%%1.2 -> 2 2.2i%%1 -> 0 2.2%%i -> Infinity 留意事項を列挙する ・operandは実数のみ対応 |
|
目次
bit演算子 |
bit演算子と付随する留意事項について記述する
bit or ・単精度32bitの符号あり整数 0|0 -> 0 0|1 -> 1 1|0 -> 1 1|1 -> 1 ・comment文に下位8桁のbit列を示す 1|1 // 00000001|00000001->00000001 -> 1 1|2 // 00000001|00000010->00000011 -> 3 2|2 // 00000010|00000010->00000010 -> 2 2|-2 // 00000010|11111110->11111110 -> -2 2|-3 // 00000010|11111101->11111111 -> -1 1|-3 // 00000001|11111101->11111101 -> -3 1|-2 // 00000001|11111110->11111111 -> -1 1|0.5 // 00000001|00000000->00000001 -> 1 1.1|0.1 // 00000001|00000000->00000001 -> 1 0|0.1 // 00000000|00000000->00000000 -> 0 bit xor ・単精度32bitの符号あり整数 0@0 -> 0 0@1 -> 1 1@0 -> 1 1@1 -> 0 ・comment文に下位8桁のbit列を示す 1@2 // 00000001^00000010->00000011 -> 3 2@-2 // 00000010^11111110->11111100 -> -4 bit and ・単精度32bitの符号あり整数 0&0 -> 0 0&1 -> 0 1&0 -> 0 1&1 -> 1 ・comment文に下位8桁のbit列を示す 1&1 // 00000001&00000001->00000001 -> 1 1&2 // 00000001&00000010->00000000 -> 0 2&2 // 00000010&00000010->00000010 -> 2 2&-2 // 00000010&11111110->00000010 -> 2 2&-3 // 00000010&11111101->00000000 -> 0 1&-3 // 00000001&11111101->00000001 -> 1 1&-2 // 00000001&11111110->00000000 -> 0 1&0.5 // 00000001&00000000->00000000 -> 0 1.1&0.1 // 00000001&00000000->00000000 -> 0 0&0.1 // 00000000&00000000->00000000 -> 0 bit shift ・単精度32bitの符号あり整数 -round(pow(2,31)) -> -2147483648 ・comment文に32桁のbit列を示す -1<<31 || -1<<63 // 10000000000000000000000000000000 -> -2147483648 -1<<30 || -1<<62 // 11000000000000000000000000000000 -> -1073741824 -1<<20 || -1<<52 // 11111111111100000000000000000000 -> -1048576 -1<<10 || -1<<42 // 11111111111111111111110000000000 -> -1024 -1<<3 || -1<<35 // 11111111111111111111111111111000 -> -8 -1<<2 || -1<<34 // 11111111111111111111111111111100 -> -4 -1<<1 || -1<<33 // 11111111111111111111111111111110 -> -2 -1>>0 || -1>>32 // 11111111111111111111111111111111 -> -1 -8>>0 || -8>>32 // 11111111111111111111111111111000 -> -8 -8>>1 || -8>>33 // 11111111111111111111111111111100 -> -4 -8>>2 || -8>>34 // 1111111111111111111111111111110 -> -2 -8>>3 || -8>>35 // 11111111111111111111111111111111 -> -1 -1>>3 || -1>>35 // 11111111111111111111111111111111 -> -1 -1>>10 || -1>>42 // 11111111111111111111111111111111 -> -1 -1>>20 || -1>>52 // 11111111111111111111111111111111 -> -1 -1>>30 || -1>>62 // 11111111111111111111111111111111 -> -1 -1>>31 || -1>>63 // 11111111111111111111111111111111 -> -1 ・単精度32bitの符号なし整数 round(pow(2,32)-1) -> 4294967295 ・comment文に32桁のbit列を示す -1>>>0 || -1>>>32 // 11111111111111111111111111111111 -> 4294967295 -8>>>0 || -8>>>32 // 11111111111111111111111111111000 -> 4294967288 -8>>>1 || -8>>>33 // 01111111111111111111111111111100 -> 2147483644 -8>>>2 || -8>>>34 // 0011111111111111111111111111110 -> 1073741822 -8>>>3 || -8>>>35 // 00011111111111111111111111111111 -> 536870911 -1>>>3 || -1>>>35 // 00011111111111111111111111111111 -> 536870911 -1>>>10 || -1>>>42 // 00000000001111111111111111111111 -> 4194303 -1>>>20 || -1>>>52 // 00000000000000000000111111111111 -> 4095 -1>>>30 || -1>>>62 // 00000000000000000000000000000011 -> 3 -1>>>31 || -1>>>63 // 00000000000000000000000000000001 -> 1 bit not ・単精度32bitの符号あり整数 ・comment文に32桁のbit列を示す ~0 // 11111111111111111111111111111111 -> -1 ~1 // 11111111111111111111111111111110 -> -2 ~-1 || (~(-1)) // 00000000000000000000000000000000 -> 0 ~-2 || (~(-2)) // 00000000000000000000000000000001 -> 1 ~-4 || (~(-4)) // 00000000000000000000000000000011 -> 3 ~-8 || (~(-8)) // 00000000000000000000000000000111 -> 7 ~3 // 11111111111111111111111111111100 -> -4 ~7 // 11111111111111111111111111111000 -> -8 ~2147483647 // 10000000000000000000000000000000 -> -2147483648 ~2147483648 // 01111111111111111111111111111111 -> 2147483647 ~2147483649 // 01111111111111111111111111111110 -> 2147483646 ~-2147483647 || (~(-2147483647)) // 01111111111111111111111111111110 -> 2147483646 ~-2147483648 || (~(-2147483648)) // 01111111111111111111111111111111 -> 2147483647 ~-2147483649 || (~(-2147483649)) // 10000000000000000000000000000000 -> -2147483648 ~-1>>>31 || ((~(-1))>>>31) // 00000000000000000000000000000000 -> 0 ~(-1>>>31) || (~(-1>>>31)) // 11111111111111111111111111111110 -> -2 bit演算子は比較演算子・関係演算子より優先する 5<2|4 || 5<(2|4) || 5<6 -> 1 4==2|4 || 4==(2|4) || 4==6 -> 0 留意事項を列挙する ・operandは実数のみ対応 ・operandは倍精度64bitから単精度32bitに変換される ・bit演算子は短絡評価しない 符号なし整数の場合、n進数⇒m進数変換参照 |
|
目次
比較演算子 |
比較演算子と付随する留意事項について記述する
比較演算子は関係演算子より優先する 1==2>1 || 1==(2>1) || 1==1 -> 1 留意事項を列挙する ・operandは実数のみ対応 ・operandに虚数を入力した場合、0と判別される i<<2 || real(i)<<2 || 0<<2 -> 0 2i>i || real(2i)>real(i) || 0>0 -> 0 ・多重比較不可 -3<-2<-1 // NG -> 0 ・論理演算子を使用 -3<-2&&-2<-1 -> 1 ・bit演算子を使用 (-3<-2)&(-2<-1) -> 1 ・Ver.2.196.46以降、論理値literalを返す 比較演算子を代替する関数は演算子代替関数参照 |
|
目次
関係演算子 |
関係演算子と付随する留意事項について記述する
等価演算子 false==0 -> 1 true==1 -> 1 ・Ver.2.167.40以降、厳密等価演算子を追加 false===0 -> 0+O(1e+0) false===FALSE -> 1 true===1 -> 0+O(1e+0) true===TRUE -> 1 ・虚数=0扱い i===0 -> 1 2i===0 -> 1 i===false -> 0+O(1e+0) ・Ver.2.847.153以降、行列の厳密等価演算子を追加 A=(1,2:3i); B=-A; A====A,A====B,A====-B,A..====-B -> (true,false,false,true) 不等価演算子 NaN<>NaN -> true false<>false -> false 0<>0 -> false false<>0 -> false true<>1 -> false ・Ver.2.225.52以降、厳密不等価演算子を追加 NaN<<>>NaN -> true false<<>>false -> false 0<<>>0 -> false false<<>>0 -> true+O(1e+0) true<<>>1 -> true+O(1e+0) ・Ver.2.847.153以降、行列の厳密不等価演算子を追加 A=(1,2:3i); B=-A; A<<<>>>A,A<<<>>>B,A<<<>>>-B,A..<<<>>>-B -> (false,true,true,false) ・論理NOT演算子||関数を使用 ~~false===0 || ~~(false===0) -> 1+O(1e+0) sne(false,0) -> 1+O(1e+0) 論理ORをbit orで代替する場合、括弧を明示||関数を使用 ・1==1 || 1==-1 LA既定時 1==1|1==-1 || 1==(1|1)==-1 || (1==1)==-1 || 1==-1 // NG -> 0 RA選択時 1==1|1==-1 || 1==(1|1)==-1 || 1==(1==-1) || 1==0 // NG -> 0 (1==1)|(1==-1) || eq(1,1)|eq(1,-1) || 1|0 -> 1 ・Ver.2.59.26以降、論理演算子を追加 1==1||1==-1 || (1==1)||(1==-1) || 1||0 -> 1 論理ANDをbit andで代替する場合、括弧を明示||関数を使用 ・1==1 && 1==-1 LA既定時 1==1&1==-1 || 1==(1&1)==-1 || (1==1)==-1 || 1==-1 // NG -> 0 RA選択時 1==1&1==-1 || 1==(1&1)==-1 || 1==(1==-1) || 1==0 // NG -> 0 (1==1)&(1==-1) || eq(1,1)&eq(1,-1) || 1&0 -> 0 ・Ver.2.59.26以降、論理演算子を追加 1==1&&1==-1 || (1==1)&&(1==-1) || 1&&0 -> 0 留意事項を列挙する ・operandは実数のみ対応 ・operandに虚数を入力した場合、0と判別される i==0 || real(i)==0 -> 1 ・多重比較不可 -2==-2==-2 // NG -> 0 ・論理演算子を使用 -2==-2&&-2==-2 -> 1 ・bit演算子を使用 (-2==-2)&(-2==-2) -> 1 ・operandに行列を入力した場合、最終要素を取り出す ・last行列関数を使用 (1,2)==(3,2) || last(1,2)==last(3,2) || 2==2 -> 1 ・代入と判別されないequal記号=は、右辺移項の中置2項演算子として扱う 2!=1 || 2=1 || =1-2 -> -1 ・よってnot equal関係演算子は!=の代わりに<>を使用する 1<>2 -> 1 ・次のような場合、関数で代替する方が間違いが少ない 2<(=2) || lt(2,=2) -> 0 2<=2 -> 1 ・Ver.2.196.46以降、論理値literalを返す 関係演算子を代替する関数は演算子代替関数参照 |
|
目次
論理NOT 演算子 |
論理NOT演算子と付随する留意事項について記述する
Ver.2.81.32以降、論理NOT演算子を追加 ~~0 -> 1 ~~1 -> 0 ~~-1 -> 0 ~~0.1 -> 0 ~~-1.3 -> 0 ~~-1.6e-1 -> 0 ~~epsilon -> 0 ・Ver.2.168.41以降、複素数に拡張 ~~i || ~~1 -> 0 ~~1+i ~~~0 || ~~(~0) || ~~(-1) -> 0 ~~~1 || ~~(~1) || ~~(-2) -> 0 ~~~-1 || ~~(~-1) || ~~(0) -> 1 (~~0||~~1) || ((~~0)||(~~1)) -> 1 (~~1||~~1) || ((~~1)||(~~1)) -> 0 ~~1<0&&2 || ((~~(1<0))&&2) -> 2 ~~1>0&&2 || ((~~(1>0))&&2) -> 0 留意事項を列挙する ・ ・Ver.2.196.46以降、論理値literalを返す |
|
目次
論理XOR 演算子 |
論理XOR演算子と付随する留意事項について記述する
Ver.2.168.41以降、論理XOR演算子を追加 0@@0 -> 0 0@@1 -> 1 1@@0 -> 1 1@@1 -> 0 0@@false || 0@@0 -> 0 0@@true || 0@@1 -> 1 0@@NaN || 0@@0 -> 0 ・複素数に拡張 0@@i || 0@@1 -> 1 1@@i || 1@@1 -> 0 i@@0 || 1@@0 -> 1 i@@1 || 1@@1 -> 0 ・Ver.2.766.116以降、xnor/cxnor関数を追加 ~~(0@@false),not(xor(0,false)),xnor(0,false) -> (true,true,true) ~~(1@@i),cnot(cxor(1,i)),cxnor(1,i) -> (true,true,true) 留意事項を列挙する ・operandは複素数に拡張 ・通常の論理演算子と異なり、2項演算子のassociativityに依存しない ・Ver.2.196.46以降、論理値literalを返す |
|
目次
論理演算子 |
論理演算子と付随する留意事項について記述する
論理OR ・LA既定 0||1 -> 1 0||1||2 -> 1 2||1||0 -> 2 2i||1i||0i -> 2i 0i||1i||2i -> i 0(1-i)||1(1-i)||2(1-i) -> 1-i 0(1-i)||1(1-i)||2(1-i)||3(1-i) -> 1-i real(0(1-i)||1(1-i)||2(1-i)||3(1-i)) -> 1 imag(0(1-i)||1(1-i)||2(1-i)||3(1-i)) -> -1 ・RA選択 0||1 -> 1 0||1||2 -> 2 2||1||0 -> 1 2i||1i||0i -> i 0i||1i||2i -> 2i 0(1-i)||1(1-i)||2(1-i) -> 2-2i 0(1-i)||1(1-i)||2(1-i)||3(1-i) -> 3-3i real(0(1-i)||1(1-i)||2(1-i)||3(1-i)) -> 3 imag(0(1-i)||1(1-i)||2(1-i)||3(1-i)) -> -3 ・Ver.2.766.116以降、nor/cnor関数を追加 ~~(0||1),not(or(0,1)),nor(0,1) -> (false,false,false) ~~(0||i),cnot(cor(0,i)),cnor(0,i) -> (false,false,false) 論理AND ・LA既定 0&&1&&2 -> 0 2&&1&&0 -> 0 1&&0&&2 -> 0 1i&&0i&&2i -> 0 1&&2&&3 -> 3 1i&&2i&&3i -> 3i 1(1-i)&&2(1-i)&&3(1-i) -> 3-3i 1(1-i)&&2(1-i)&&3(1-i)&&4(1-i) -> 4-4i real(1(1-i)&&2(1-i)&&3(1-i)&&4(1-i)) -> 4 imag(1(1-i)&&2(1-i)&&3(1-i)&&4(1-i)) -> -4 1(1-i)||2(1-i)&&3(1-i)&&4(1-i) -> 1-i 1(1-i)&&2(1-i)||3(1-i)&&4(1-i) -> 2-2i 1(1-i)&&2(1-i)&&3(1-i)||4(1-i) -> 3-3i ・RA選択 0&&1&&2 -> 0 2&&1&&0 -> 0 1&&0&&2 -> 0 1i&&0i&&2i -> 0 1&&2&&3 -> 1 1i&&2i&&3i -> i 1(1-i)&&2(1-i)&&3(1-i) -> 1-i 1(1-i)&&2(1-i)&&3(1-i)&&4(1-i) -> 1-i real(1(1-i)&&2(1-i)&&3(1-i)&&4(1-i)) -> 1 imag(1(1-i)&&2(1-i)&&3(1-i)&&4(1-i)) -> -1 1(1-i)||2(1-i)&&3(1-i)&&4(1-i) -> 2-2i 1(1-i)&&2(1-i)||3(1-i)&&4(1-i) -> 3-3i 1(1-i)&&2(1-i)&&3(1-i)||4(1-i) -> 4-4i ・Ver.2.766.116以降、nand/cnand関数を追加 ~~(1&&2),not(and(1,2)),nand(1,2) -> (false,false,false) ~~(1i&&2i),cnot(cand(1i,2i)),cnand(1i,2i) -> (false,false,false) 論理演算子は最下位の演算子のprecedenceで変数への代入より優先する clear; x=<a=3; (0||x=>||2,a) // (0||0||2,3) -> (2,3) clear; x=<a=3; (0||x=>||a) // (0||0||3) -> 3 clear; x=<a=3; (0||(x=>)||a) // (0||0||3) -> 3 clear; 0||(a=3)||a // 0||0||3 -> 3 clear; 0||(a=3)||(a=-3)||a // 0||0||0||-3 -> -3 clear; a=3||3,a // a=(3||3),a -> (0,3) clear; 1||a=3 // (1||a)=3 -> [MyErr]Invalid binary operation clear; 1||=3 // (1||)=3 -> [MyErr]Invalid binary operation clear; 1||0=3 // (1||0)=3 -> 2 clear; 0||0=3 // (0||0)=3 -> 3 clear; i||0=3 // (i||0)=3 -> 3-i clear; 0||i=3 // (0||i)=3 -> 3-i 論理AND||OR演算子の留意事項を列挙する ・論理AND演算子は全operandを評価してfalse判定値の短絡評価を再現する ・論理OR演算子は全operandを評価してnot(false判定値)の短絡評価を再現する ・LA既定の場合、中置2項演算子のright-operandよりleft-operandを優先して左から評価する ・RA選択の場合、中置2項演算子のleft-operandよりright-operandを優先して右から評価する 論理ORを厳密に短絡評価して処理を切替える場合 ・switch高階関数を使用 clear; set_a0=<a=0; set_a1=<a=1; switch(1,set_a0=>:1,set_a1=>); a // NG -> 1 clear; set_a0=<a=0; set_a1=<a=1; switch(1,=<set_a0=>:1,=<set_a1=>); a // OK -> 0 clear; set_a0=<a=0; set_a1=<a=1; switch(0,=<set_a0=>:1,=<set_a1=>); a // OK -> 1 ・Ver.2.157.38以降、switch高階関数代替の論理演算子(短絡評価)を追加 clear; set_a0=<a=0; set_a1=<a=1; set_a2=<a=2; set_a0=>|||set_a1=>|||set_a2=>; a -> 2 clear; set_a0=<a=0; set_a1=<a=1; set_a2=<a=2; ~~(set_a0=>)|||set_a1=>|||set_a2=>; a -> 0 clear; set_a0=<a=0; set_a1=<a=1; set_a2=<a=2; set_a0=>&&&set_a1=>&&&set_a2=>; a -> 0 clear; set_a0=<a=0; set_a1=<a=1; set_a2=<a=2; ~~(set_a0=>)&&&set_a1=>&&&set_a2=>; a -> 1 |
|
目次
論理演算子 (短絡評価) |
論理演算子(短絡評価)と付随する留意事項について記述する
・通常の論理演算子と区別してANDs||ORsと表記する ・Ver.2.258.60以降、operandを拡張 operand:変数 ⇒ 変数・式変数 論理演算子(短絡評価)は式変数への式代入直後の演算のprecedenceで最上位関数より優先する 実装の詳細は内部仕様参照 論理ORs ・LA既定 0|||1 -> 1 0|||1|||2 -> 1 2|||1|||0 -> 2 2i|||1i|||0i -> 2i 0i|||1i|||2i -> i 0(1-i)|||1(1-i)|||2(1-i) -> 1-i 0(1-i)|||1(1-i)|||2(1-i)|||3(1-i) -> 1-i real(0(1-i)|||1(1-i)|||2(1-i)|||3(1-i)) -> 1 imag(0(1-i)|||1(1-i)|||2(1-i)|||3(1-i)) -> -1 (0,0)|||1 -> (0,0) clear; (a=0)|||hasVar(a) -> 1 clear; x=1; y=<x|||1/0|||-x; y -> 1 clear; x=(1,2); y=<x|||1/0|||-x; y -> (1,2) clear; x=1; y=x|||1/0|||-x; y -> 1 clear; x=1; y=<x|||1/0|||-x; y -> 1 clear; x=1; y=(x|||1/0)|||-x; y -> 1 clear; x=1; y=x|||(1/0|||-x); y -> 1 clear; x=1; y=~~x|||1/0|||~~-x; y -> 0 clear; x=1; y=~~(x|||1/0)|||~~-x; y -> 0 clear; x=1; y=~~x|||(1/0|||~~-x); y -> 0 clear; x=1; y=~~x|||y|||~~-x; y -> [MyErr]Undef var||| clear; x=1; y=~~x|||x=>|||~~-x; y -> [MyErr]Invalid REv(x) clear; x=<0|||y=3; x,y -> [MyErr]Invalid REv(y) clear; x=<0|||(y=3); x,y -> (0,3) clear; (x=2)|||1|||x; x -> 2 clear; x=(1,2); y=<1&&&x|||1/0|||-x&&&0; y -> (1,2) clear; x=(1,2); y=<{0&&&x|||Infinity|||-x&&&1}; y -> Infinity ・RA選択 0|||1 -> 1 0|||1|||2 -> 2 2|||1|||0 -> 1 2i|||1i|||0i -> i 0i|||1i|||2i -> 2i 0(1-i)|||1(1-i)|||2(1-i) -> 2-2i 0(1-i)|||1(1-i)|||2(1-i)|||3(1-i) -> 3-3i real(0(1-i)|||1(1-i)|||2(1-i)|||3(1-i)) -> 3 imag(0(1-i)|||1(1-i)|||2(1-i)|||3(1-i)) -> -3 (0,0)|||1 -> 1 clear; (a=0)|||hasVar(a) -> 0 clear; x=1; y=<x|||1/0|||-x; y -> -1 clear; x=(1,2); y=<x|||1/0|||-x; y -> (-1,-2) clear; x=1; y=x|||1/0|||-x; y -> -1 clear; x=1; y=<x|||1/0|||-x; y -> -1 clear; x=1; y=(x|||1/0)|||-x; y -> -1 clear; x=1; y=x|||(1/0|||-x); y -> -1 clear; x=1; y=~~x|||1/0|||~~-x; y -> 0 clear; x=1; y=~~(x|||1/0)|||~~-x; y -> 0 clear; x=1; y=~~x|||(1/0|||~~-x); y -> 0 clear; x=1; y=~~x|||y|||~~-x; y -> [MyErr]Undef |||var clear; x=1; y=~~x|||x=>|||~~-x; y -> [MyErr]Undef |||var clear; x=<0|||y=3; x,y -> [MyErr]Invalid REv clear; x=<0|||(y=3); x,y -> (0,3) clear; (x=2)|||1|||x; x -> [MyErr]Undef |||var clear; x=(1,2); y=<1&&&x|||1/0|||-x&&&0; y -> 1 clear; x=(1,2); y=<{0&&&x|||Infinity|||-x&&&1}; y -> (-1,-2) 論理ANDs ・LA既定 0&&&1&&&2 -> 0 2&&&1&&&0 -> 0 1&&&0&&&2 -> 0 1i&&&0i&&&2i -> 0 1&&&2&&&3 -> 3 1i&&&2i&&&3i -> 3i 1(1-i)&&&2(1-i)&&&3(1-i) -> 3-3i 1(1-i)&&&2(1-i)&&&3(1-i)&&&4(1-i) -> 4-4i real(1(1-i)&&&2(1-i)&&&3(1-i)&&&4(1-i)) -> 4 imag(1(1-i)&&&2(1-i)&&&3(1-i)&&&4(1-i)) -> -4 1(1-i)|||2(1-i)&&&3(1-i)&&&4(1-i) -> 1-i 1(1-i)&&&2(1-i)|||3(1-i)&&&4(1-i) -> 2-2i 1(1-i)&&&2(1-i)&&&3(1-i)|||4(1-i) -> 3-3i (0,0)&&&1 -> 1 clear; (a=0)&&&hasVar(a) -> 0 clear; x=1; y=<x&&&1/0&&&-x; y -> NaN clear; x=(1,2); y=<x&&&-i&&&-x; y -> (-1,-2) clear; x=1; y=x&&&-i&&&-x; y -> -1 clear; x=1; y=<x&&&-i&&&-x; y -> -1 clear; x=1; y=(x&&&-i)&&&-x; y -> -1 clear; x=1; y=x&&&(-i&&&-x); y -> -1 clear; x=1; y=~~x&&&-i&&&~~-x; y -> 0 clear; x=1; y=~~(x&&&-i)&&&~~-x; y -> 0 clear; x=1; y=~~x&&&(-i&&&~~-x); y -> 0 clear; x=1; y=~~x&&&y&&&~~-x; y -> 0 clear; x=1; y=~~x&&&x=>&&&~~-x; y -> 0 clear; x=<0&&&y=3; x,y -> [MyErr]Invalid REv(y) clear; x=<0&&&(y=3); x,y -> [MyErr]Invalid REv(y) clear; (x=2)&&&1&&&x; x -> 2 clear; x=(1,2); y=<1|||x&&&1/0&&&-x|||0; y -> 1 clear; x=(1,2); y=<{0|||x&&&Infinity&&&-x|||1}; y -> (-1,-2) ・RA選択 0&&&1&&&2 -> 0 2&&&1&&&0 -> 0 1&&&0&&&2 -> 0 1i&&&0i&&&2i -> 0 1&&&2&&&3 -> 1 1i&&&2i&&&3i -> i 1(1-i)&&&2(1-i)&&&3(1-i) -> 1-i 1(1-i)&&&2(1-i)&&&3(1-i)&&&4(1-i) -> 1-i real(1(1-i)&&&2(1-i)&&&3(1-i)&&&4(1-i)) -> 1 imag(1(1-i)&&&2(1-i)&&&3(1-i)&&&4(1-i)) -> -1 1(1-i)|||2(1-i)&&&3(1-i)&&&4(1-i) -> 2-2i 1(1-i)&&&2(1-i)|||3(1-i)&&&4(1-i) -> 3-3i 1(1-i)&&&2(1-i)&&&3(1-i)|||4(1-i) -> 4-4i (0,0)&&&1 -> (0,0) clear; (a=0)&&&hasVar(a) -> 0 clear; x=1; y=<x&&&1/0&&&-x; y -> NaN clear; x=(1,2); y=<x&&&-i&&&-x; y -> (1,2) clear; x=1; y=x&&&-i&&&-x; y -> 1 clear; x=1; y=<x&&&-i&&&-x; y -> 1 clear; x=1; y=(x&&&-i)&&&-x; y -> 1 clear; x=1; y=x&&&(-i&&&-x); y -> 1 clear; x=1; y=~~x&&&-i&&&~~-x; y -> 0 clear; x=1; y=~~(x&&&-i)&&&~~-x; y -> 0 clear; x=1; y=~~x&&&(-i&&&~~-x); y -> 0 clear; x=1; y=~~x&&&y&&&~~-x; y -> 0 clear; x=1; y=~~x&&&x=>&&&~~-x; y -> 0 clear; x=<0&&&y=3; x,y -> [MyErr]Undef &&&var clear; x=<0&&&(y=3); x,y -> (0,3) clear; (x=2)&&&1&&&x; x -> [MyErr]Undef &&&var clear; x=(1,2); y=<1|||x&&&1/0&&&-x|||0; y -> 1 clear; x=(1,2); y=<{0|||x&&&Infinity&&&-x|||1}; y -> 1 通常の論理演算子と異なり、拡張行列演算の対象外 0&&(1,1) || (0&&1,0&&1) -> (0,0) LA既定 0||(1,0:0,1)||(2,3) || ((0||1,0||0)||(2,3):(0||0,0||1)||(2,3)) -> (1,3:2,1) RA選択 0||(1,0:0,1)||(2,3) || ((0||1,0||0)||(2,3):(0||0,0||1)||(2,3)) -> (2,3:2,3) 0&&&(1,1) -> 0 LA既定 0|||(1,0:0,1)|||(2,3) -> (1,0:0,1) RA選択 0|||(1,0:0,1)|||(2,3) -> (2,3) ・Ver.2.158.38以降、無次元の演算に対応 LA既定 0|||(1,0:0,1)|||(2,3) -> 1 RA選択 0|||(1,0:0,1)|||(2,3) -> 3 Ver.2.158.38以降、NaNに対応 ・LA既定 NaN||1 || NaN|||1 -> 1 NaN&&1 || NaN&&&1 -> NaN NaN|1 -> 1 NaN&1 -> 0 ~NaN || ~0 -> -1 ~~NaN || ~~(~~true) -> 1 Ver.2.165.40以降、falseに対応 ・LA既定 false|||1 -> 1 false&&&1 -> false Ver.2.258.60以降、operandを拡張 ・((x)=>x)||false // ES2015 -> (x)=>x ((x)=<x)|||false -> [MyErr]Invalid BTe([object Object]) (=<(x)=<x)|||false -> [MyErr]Invalid BTe([object Object],[object Object]) ・(((x)=>x)||false)(2) // ES2015 -> 2 (((x)=<x)|||false)(2) -> [MyErr]Invalid FN operation (((x)=<x)|||false)(2)=> -> 2 ・pipe clear; ((=<(x)=<x)|||false)(2)=> -> [MyErr]Invalid args.length=0(no-name) clear; (((=<(x)=<x)|||false)=>)(2)=> -> 2 ・=< ⇔ 遅延評価のreturn clear; (((()=<(x)=<x)|||false)()=>)(2)=> -> 2 ・a=-1; (((a=>b=>[a,b])||false)(1))(2) // ES2015 -> [1, 2] clear; ((((a)=<(b)=<(a,b))|||false)(1)=>)(2)=> -> (1,2) clear; a=-1; ((((a/*not-closed*/)=<(b)=<(a,b))|||false)(1)=>)(2)=> -> (-1,2) ・Ver.2.262.62以降、define判別idが消失する致命的な不具合を修正(値のid ⇒ nameのid継承) clear; $a=-1; ((((a)=<(b)=<(a,b))|||false)(1)=>)(2)=> -> ・単独scope clear; a=-1; ((((a/*closed@1st-call*/)=<[(b)=<(a,b)])|||false)(1)=>)(2)=> -> (1,2) clear; a=-1; (([(a/*closed@1st-call*/)=<(b)=<(a,b)]|||false)(1)=>)(2)=> -> (1,2) clear; a=-1; ([((a/*closed@1st-call*/)=<(b)=<(a,b))|||false](1)=>)(2)=> -> (1,2) clear; a=-1; [(((a/*closed@1st-call*/)=<(b)=<(a,b))|||false)(1)=>](2)=> -> (1,2) ・nest clear; (((x)=<((=<x)|||false)=>)|||false)(2)=> -> 2 clear; (((x)=<((()=<x)|||false)()=>)|||false)(2)=> -> 2 ・((b=>((a=>[a,b])||false)(1))||false)(2) // ES2015 -> [1, 2] clear; (((b)=<(((a)=<[a,b])|||false)(1)=>)|||false)(2)=> -> (1,2) 論理ANDs||ORs演算子の留意事項を列挙する ・可読性に難あり ・代入処理は括弧を明示する方が間違いが少ない(short_circuit参照) clear; a=<b=1&&&c=2; a=> -> [MyErr]Invalid operation clear; a=<b=1&&&(c=2); a=>; b,c -> (0,2) clear; a=<(b=1)&&&(c=2); a=>; b,c -> [MyErr]Invalid REv(c) clear; a=<(b=1)|||(c=2); a=>; b,c -> (1,2) clear; a=0|||b=1&&&c=2 -> [MyErr]Invalid ans isFound clear; a=0|||~~(b=1)&&&(c=2)|||3; a,b,c -> (3,1,2) clear; (a=0)|||~~(b=1)&&&(c=2)|||3; a,b,c -> (0,1,2) ・通常の論理演算子と異なる点を列挙する ・有次元の拡張行列演算の対象外 ・演算子のprecedenceを変更不可(内部optionの対象外) ・switch高階関数を代替可(低負荷の一方、難読化の可能性あり) ・論理ANDs演算子は厳密にfalse判定値を短絡評価する operand=false判定値以降、評価を省略 ・論理ORs演算子は厳密にnot(false判定値)を短絡評価する operand=not(false判定値)以降、評価を省略 ・operand省略時、error終了 0&& -> [MyErr]Invalid binary operation ||0 -> [MyErr]Invalid binary operation 0&&& -> [MyErr]Invalid binary operation |||0 -> [MyErr]Invalid binary operation &&& -> [MyErr]Invalid binary operation ||| -> [MyErr]Invalid binary operation |
|
目次
論理演算子 (literal) |
論理演算子(literal)と付随する留意事項について記述する
・通常の論理演算子と区別してANDss||ORssと表記する ・Ver.2.258.60以降、operandを拡張 operand:変数 ⇒ 変数・式変数 Ver.2.196.46以降、条件演算子代替のANDss||ORss演算子を追加 ・0を返す代入処理と論理値literalを返す関数||演算子を活用 論理ORss ・LA既定 0||||1 -> 0 false||||1 -> 1 NaN||||1 -> 1 ・RA選択 0||||1 -> 1 false||||1 -> 1 NaN||||1 -> 1 論理ANDss ・LA既定 0&&&&1 -> 1 false&&&&1 -> false NaN&&&&1 -> NaN ・RA選択 0&&&&1 -> 0 false&&&&1 -> false NaN&&&&1 -> NaN 論理ANDss||ORss演算子の留意事項を列挙する ・可読性に難あり ・論理演算子(短絡評価)と異なる点を列挙する ・論理ANDss演算子は厳密にfalse||NaNを短絡評価する ・論理ORss演算子は厳密にnot(false||NaN)を短絡評価する |
|
目次
条件演算子 |
条件演算子と付随する留意事項について記述する
条件演算子は未実装で代替案を示す switch高階関数 ・Nativeの一例 var y = ((x < 0)? -x: x); ・値渡し y=<switch(x<0,-x:1,x); y=<switch(lt(real(x),0),-real(x):1,real(x)); x=2; y -> 2 x=-2; y -> 2 ・式渡し y=<switch(x<0,=<-x:1,=<{x}); y=<switch(lt(real(x),0),=<-real(x):1,=<real(x)); x=2; y -> 2 x=-2; y -> 2 ・式変数を使用 cond_m=<lt(real(x),0); proc_m=<-real(x); cond_p=<1; proc_p=<real(x); x=-2; (cond_m,proc_m:cond_p,proc_p) -> (1,2:1,-2) x=-2; switch(cond_m,proc_m:cond_p,proc_p) -> 2 x=-2; (cond_m,=<proc_m:cond_p,=<proc_p) -> [MyErr]Invalid BTe([object Object]) x=-2; switch(cond_m,=<proc_m:cond_p,=<proc_p) -> 2 ・値渡し cp_m=<(cond_m,proc_m); cp_p=<(cond_p,proc_p); cp_mp=<(cp_m:cp_p); x=-2; (cp_mp) -> (1,2:1,-2) x=-2; switch(cp_mp) -> 2 ・式渡し cp_m=<(cond_m,=<proc_m); cp_p=<(cond_p,=<proc_p); cp_mp=<(cp_m:cp_p); x=-2; (cp_mp) -> [MyErr]Invalid BTe([object Object]) x=-2; switch(cp_mp) -> 2 論理演算子(短絡評価) ・left||rightのexpressionを分岐するPython記法の一例(LA既定) sw_equation(isLeft,=<left,=<right)=<(isLeft&&&{left=>,}|||{right=>,})[0]; sw_equation(false,=<0,=<1) || sw_equation(0,=<0,=<1) -> 1 sw_equation(true,=<0,=<1) || sw_equation(1,=<0,=<1) -> 0 ・無次元の場合、left=0を返却不能の対策が必要 sw_NG(isLeft)=<isLeft&&&{=<0}=>|||{=<1}=>; sw_NG(false),sw_NG(true) -> (1,1) sw_OK(isLeft)=<isLeft&&&~~(left=2)|||~~(right=3); sw_OK(false),right -> (1,3) sw_OK(true),left -> (1,2) ・Ver.2.196.46以降、論理演算子(literal)を追加 sw_OK(isLeft)=<isLeft&&&&{=<0}=>||||{=<1}=>; sw_OK(false),sw_OK(true) -> (1,0) sw_OK(isLeft)=<isLeft&&&&(left=2)||||(right=3); sw_OK(false),right -> (0,3) sw_OK(true),left -> (0,2) ・有次元の場合、対策不要 sw_mat(isLeft,=<left,=<right)=<(isLeft&&&left=>|||right=>); l=<[a=1,a:2a,3a]; r=<[a=-1,a:2a,3a]; sw_mat(false,=<l,=<r),sw_mat(true,=<l,=<r),sw_mat(0,=<l,=<r)+sw_mat(1,=<l,=<r) -> ( 0,-1,0,1,0,0: -2,-3,2,3,0,0 ) |
|
目次
浮動小数点 演算 |
JavaScriptによる実数の浮動小数点演算について記述する
・Ver.2.139.35以降、最新の演算結果と本manual一部の記述内容にMachine epsilon程度の相違がある JavaScriptのNumber型はIEEE754規格の倍精度64bit2進形式の浮動小数点数を使用する ・浮動小数点数による演算を以降、浮動小数点演算と呼ぶ ・64bitの上位から順に3つのfield(符号部・指数部・仮数部)を持つ 10進換算の浮動小数点数 =(-1)^(符号部1bit)*pow(基数2,指数部11bit-bias)*(0||1+仮数部52bit) ・指数部・仮数部は符号なしの2進数 ・指数部は符号ありを符号なしに変換する次のbiasを持つ bias=2^(11-1)-1=1023 ・pow関数(base,exponent)はbase^exponentのNative関数 ・10進換算の指数に相当する pow(2,10) || 2^10 || 1024 -> 1.024e3 ・仮数部が小数点以下の有効桁を保持する(10進換算の有効数字の最大桁数≒16) ・10進換算で有効数字の実数演算結果を示す(最上位bitから最下位bitまで) pow(2,-1) || 2^(-1) -> 0.5 pow(2,-2) || 2^(-2) -> 0.25 ... pow(2,-51) || 2^(-51) -> 4.440892098500626e-16 pow(2,-52) || 2^(-52) -> 2.220446049250313e-16 ・この最小値O(1e-16)より小さな有効数字は保持できない ・これを丸める誤差をMachine epsilonと呼ぶ 64bit2進形式の浮動小数点演算の挙動を示す ・16桁の小数を入力した場合、同じ 0.9999999999999999 -> 0.9999999999999999 -0.9999999999999999 -> -0.9999999999999999 ・17桁の小数を入力した場合、Machine epsilonが生じる 0.99999999999999999 -> 1 -0.99999999999999999 -> -1 ・整数も小数同様に、Number型で保存される ・よって17桁以上の整数を入力した場合、Machine epsilonが生じる 9007199254740991 -> 9007199254740991 90071992547409911 -> 90071992547409900 900719925474099111 -> 900719925474099100 9007199254740991111 -> 9007199254740991000 90071992547409911111 -> 90071992547409900000 900719925474099111111 -> 900719925474099100000 9007199254740991111111 -> 9.007199254740991e+21 ・1000で割って1000を掛けた場合、Machine epsilonが生じる 9007199254740991/1000 -> 9007199254740.99 ans*1000 -> 9007199254740990 0.9999999999999999/1000 -> 0.0009999999999999998 ans*1000 -> 0.9999999999999998 ・実数演算の場合、2の累乗倍で演算すれば仮数部の有効桁が保持される 9007199254740991/1024 -> 8796093022207.999 ans*1024 -> 9007199254740991 9007199254740991/2^100 -> 7.105427357601001e-15 ans*2^100 -> 9007199254740991 9007199254740991/2^(-100) -> 1.1417981541647678e+46 ans*2^(-100) -> 9007199254740991 0.9999999999999999/1024 -> 0.0009765624999999999 ans*1024 -> 0.9999999999999999 0.9999999999999999/2^100 -> 7.888609052210117e-31 ans*2^100 -> 0.9999999999999999 0.9999999999999999/2^(-100) -> 1.2676506002282293e+30 ans*2^(-100) -> 0.9999999999999999 |
|
目次
Machine epsilon |
浮動小数点演算のMachine epsilonについて記述する
仮数部の最下位bitの有効数字未満を丸める相対誤差をMachine epsilonと呼ぶ ・次のepsilonで定義する epsilon || eps || pow(2,-52) -> 2.220446049250313e-16 ・test caseを列挙する 1+epsilon -> 1.0000000000000002 1+epsilon/2 -> 1 10+10epsilon -> 10.000000000000002 10+10epsilon/2 -> 10.000000000000002 10+10epsilon/4 -> 10 100+100epsilon/4 -> 100 1000+1000epsilon/4 -> 1000 1e4+1e4epsilon/4 -> 10000 1-epsilon -> 0.9999999999999998 1-epsilon/2 -> 0.9999999999999999 1-epsilon/4 -> 1 10-10epsilon/4 -> 10 100-100epsilon/4 -> 100 1000-1000epsilon/4 -> 1000 1e4-1e4epsilon/4 -> 10000 |
|
目次
Number型 定数 |
Number型の定数について記述する
JavaScriptのNumber型の定数を定義して列挙する EPSILON -> 2.220446049250313e-16 MIN_SAFE_INTEGER || -(2^53-1) -> -9007199254740991 MAX_SAFE_INTEGER || +(2^53-1) -> 9007199254740991 MIN_VALUE -> 5e-324 MAX_VALUE -> 1.7976931348623157e+308 INF || INFINITY || POSITIVE_INFINITY -> Infinity NINF || NINFINITY || NEGATIVE_INFINITY -> -Infinity ln2 -> 0.6931471805599453 ln10 -> 2.302585092994046 log2e -> 1.4426950408889634 log10e -> 0.4342944819032518 sqrt1_2 -> 0.7071067811865476 sqrt2 -> 1.4142135623730951 e -> 2.718281828459045 pi -> 3.141592653589793 test caseを列挙する MIN_VALUE/2 -> 0 MIN_VALUE*(1-EPSILON) -> 5e-324 MAX_VALUE*2 -> Infinity MAX_VALUE*(1+EPSILON) -> Infinity ・Nativeの場合 Math.pow(2,Math.pow(2,10)) || 2**(2**10) -> Infinity ・実数演算の場合、Nativeに同義 pow(2,pow(2,10)) || 2**(2**10) || 2^(2^10) -> Infinity ・複素数演算の場合、MAX_VALUEに近い値が得られる pow(2,pow(2,10)) || 2**(2**10) || 2^(2^10) -> 1.7976931348622732e+308 (1+106epsilon)2^(2^10) -> 1.7976931348623155e+308 (1+107epsilon)2^(2^10) -> Infinity |
|
目次
literal |
literalについて記述する
JavaScriptのliteralの一部を定義して列挙する ・実数値以外の非数NaN(Not a Number) NaN || nan || NAN -> NaN ・論理値 false || FALSE -> false true || TRUE -> true ・Ver.2.161.39以降、指数表記選択の場合、error終了を修正 test caseを列挙する false==false || FALSE==0 -> 1 true==true || TRUE==1 -> 1 NaN==NaN -> 0 NaN*0 || NaN*i -> NaN 0/0 -> NaN 1/0 -> NaN ・実数演算 1/0 -> Infinity ・Ver.2.184.44以降、auto-real selected時 1/0 -> Infinity 留意事項を列挙する ・isNaN判定の方法を示す NaN==NaN -> 0 x=NaN; x<>x || ~~(x==x) -> 1 isNaN_(x)=<(x<>x); isNaN_(NaN),isNaN_(Infinity) -> (1,0) a=0; b=a/a; c=1/a; isNaN_(a),isNaN_(b),isNaN_(c) -> (0,1,1) ・Ver.2.159.38以降、isNaN関数を追加 a=0; b=a/a; c=1/a; isNaN(a),isNaN(b),isNaN(c) -> (false,true,true) ・実数演算 a=0; b=a/a; c=1/a; isNaN_(a),isNaN_(b),isNaN_(c) -> (0,1,0+O(1e+0)) a=0; b=a/a; c=1/a; isNaN(a),isNaN(b),isNaN(c) -> (false,true,false+O(1e+0)) |
|
目次
関数list |
論理値literalのみを返す関数を列挙する
・Ver.2.159.38以降、isNaN関数 ・Ver.2.172.42以降、isFalse/isTrue行列関数 ・Ver.2.196.46以降、最上位関数 ・Ver.2.196.46以降、演算子代替関数 |
|
目次
演算子list |
Ver.2.196.46以降、論理値literalのみを返す演算子を列挙する
・比較演算子 ・関係演算子 ・論理NOT演算子 ・論理XOR演算子 |
|
目次
誤差の扱い |
誤差の種類とその扱いについて記述する
本manualでは大きく分けて次の2種類に分類する ・丸め誤差: 計算機での数値表現由来の誤差 ・情報落ち(絶対値の大きく異なる2つの数値の差||和を取る場合) ・桁落ち(丸め誤差を含む同符号の2つの近い数値の差を取る場合) ・Rumpの例題の要求桁数>10進数で37桁(Rump参照) ・数値誤差: 数学的な近似由来の誤差 ・離散化誤差(微分・積分の無限小を有限の幅で離散化する場合) ・打切り誤差(絶対収束する無限級数を有限の次数で打切る場合) ・modelling誤差(数値誤差を許容して対象を理論的にmodel化する場合) 丸め誤差は無理数等を仮数部の有効桁に丸める際の、 近似値の真値に対する絶対誤差||相対誤差と定義する ・円周率20桁の演算結果を一例に示す 3.14159265358979323846 -> 3.141592653589793 pi -> 3.141592653589793 ・円周率20桁の絶対誤差はMachine epsilonに相当する 0.00000000000000023846 -> 2.3846e-16 epsilon -> 2.220446049250313e-16 ・円周率20桁の相対誤差 0.00000000000000023846/pi -> 7.590417545938672e-17 2つの数値の減算||加算で情報落ちが発生した場合、警告文を表示する ・警告文は前置のinfoLost[実部r虚部i]とする 1+1e-16 -> infoLost[r ] 1 (1-1e-16)i -> infoLost[r ] 0.9999999999999999i i+1e-16i -> infoLost[ i] i 1-1e-16+i-1e-16i -> infoLost[ri] 0.9999999999999999+0.9999999999999999i 1+epsilon -> 1.0000000000000002 1+epsilon/2 -> infoLost[r ] 1 1-epsilon -> 0.9999999999999998 1-epsilon/2 -> infoLost[r ] 0.9999999999999999 虚数単位iを求める複素数演算を一例に誤差情報の特徴を示す (-1)^0.5 -> 6.123233995736766e-17+i ・実部にMachine epsilonが残るため、1を加算すると情報落ちが発生する ans+1 -> infoLost[r ] 1+i ・さらに演算を繰り返すと、誤差情報は消えることなく伝播する ans+1 -> infoLost[r ] 2+i ans+1 -> infoLost[r ] 3+i ans+1 -> infoLost[r ] 4+i ans+1 -> infoLost[r ] 5+i ・真値が0との乗算では本来、誤差情報も消えるが、逐次判定しないため、誤差情報が残る ans*0 -> infoLost[r ] 0 桁落ちは判定困難で評価にかかる演算量を見積もれないため、評価しない ・整数演算を一例に示す ・丸め誤差を含む2つの整数を作る ・comment文に有効桁のbit列を示す 255 // 11111111 -> 255 255>>2 // 111111 -> 63 ans<<2 // 11111100 -> 252 255>>3 // 11111 -> 31 ans<<3 // 11111000 -> 248 ・2つの整数の差を取ると有効桁が減少して丸め誤差が拡大する 252-248 // 100 -> 4 |
|
目次
数値解の 数値誤差 |
数値解の数値誤差について記述する
Computer Algebra Systemで解析的に真値||厳密解||解析解が得られない場合 ・数値誤差を許容した数値解を得る(例えば、微分・積分) ・applicationの数値解のthroughputを優先するため、Computer Algebra System未実装 ・よって解析解が得られるcaseも数値誤差を許容する 詳細は未実装のCAS参照 無限を有限で数学的に近似する際、数値誤差の定義を列挙する ・近似値の真値に対する絶対誤差||相対誤差 ・近似解の厳密解に対する絶対誤差||相対誤差 ・数値解の解析解に対する絶対誤差||相対誤差(以降、解析誤差と呼ぶ) 数値誤差は目安の解析誤差(絶対誤差)のOrderを表示する ・Order表示は後置の+O(実部+虚部i)とする ・目安のため、解のdouble-checkが必要 f(x)=x^2のx=1+iにおける1階微分の数値解 x=1+i; _dx(=<{x^2}) -> 1.9999999999996223+1.9999999999996223i+O(1e-12+1e-12i) ・上記微分の解析解 x=1+i; 2x -> 2+2i ・変数を使用 ansn=1.9999999999996223+1.9999999999996223i; ansa=2+2i; dans=ansn-ansa; ・絶対誤差 erra=abs(real(dans))+abs(imag(dans))i; erra -> 3.7769787297747826e-13+3.7769787297747826e-13i ・絶対誤差のEuclidean norm normc(erra) -> 5.341454544442203e-13 ・相対誤差 errr=abs(real(erra)/real(ansa))+abs(imag(erra)/imag(ansa))i; errr -> 1.8884893648873913e-13+1.8884893648873913e-13i ・相対誤差のEuclidean norm normc(errr) -> 2.6707272722211015e-13 f(x)=x^4の積分区間[0,1+i]における定積分の数値解 a=0; b=1+i; _ix(=<{x^4},a,b) || ab=[0,1+i]; _ix(=<{x^4},ab) -> -0.8000000053333336-0.8000000053333334i+O(1e-8+1e-8i) ・解析解 a=0; b=1+i; (b^5-a^5)/5 -> -0.8000000000000003-0.8000000000000002i ・変数を使用 ansn=-0.8000000053333336-0.8000000053333334i; ansa=-0.8000000000000003-0.8000000000000002i; dans=ansn-ansa; ・絶対誤差 erra=abs(real(dans))+abs(imag(dans))i; erra -> 5.333333330526102e-9+5.3333332195038e-9i ・絶対誤差のEuclidean norm normc(erra) -> 7.54247225018186e-9 ・相対誤差 errr=abs(real(erra)/real(ansa))+abs(imag(erra)/imag(ansa))i; errr -> 6.666666663157625e-9+6.666666524379749e-9i ・相対誤差のEuclidean norm normc(errr) -> 9.428090312727323e-9 数値誤差の特徴を示す ・数値誤差を含む演算結果に対して x=1+i; _dx(=<{x^2}) -> 1.9999999999996223+1.9999999999996223i+O(1e-12+1e-12i) ・演算すると目安の解析誤差も演算される ans*1e3 -> 1999.9999999996223+1999.9999999996223i+O(1e-9+1e-9i) ans/1e3 -> 1.9999999999996223+1.9999999999996223i+O(1e-12+1e-12i) ans*ans -> 7.999999999996978i+O(8e-12i) sinh(ans) -> 0.9893582466238214i+O(1e-12i) ・解析誤差は符号がないため、減算||加算では誤差の最大値を選択する ans+2ans -> 2.968074739871464i+O(2e-12i) ans-2ans -> -2.968074739871464i+O(5e-12i) ・真値が0との乗算では、目安の解析誤差も消える ans*0 -> 0 |
|
目次
演算flow |
演算実行確定1回の演算flowについて記述する
次の3関数による演算flowを示す main関数 ⇔ parse関数 ⇔ operation関数 ・main関数 pre処理:入力dataを作ってparse関数に渡す post処理:出力dataから演算結果を外部に表示する ・parse関数 pre処理:入力dataから実行文を作ってoperation関数に渡す post処理:演算結果から出力dataを作ってmain関数に返す ・operation関数 run処理:実行文から演算結果を作ってparse関数に返す parse関数とoperation関数の役割分担を示す parse関数の役割はcompiler ・括弧のnestingによる構文を解析し、深さ方向にtree構造を階層化する ・Ver.2.228.56以降、式渡しも同様に、括弧に変換して階層化 ・入力dataの字句を解析してtagを付ける ・逐次、入力dataを実行文のtreeに置換する operation関数の役割はinterpreter ・演算のprecedenceに従って実行文を実行する ・逐次、実行文のtreeを演算結果のtreeに置換する ・再帰的に単位tree構造に帰結する |
|
目次
演算仕様 |
演算量||演算速度に関係する演算仕様の概要について記述する
UI設定によって対応する用途を4種類示す ・有次元の複素数の行列演算(complex selected && matrix checked) ・有次元の実数の行列演算(real selected && matrix checked) ・無次元の複素数演算(complex selected && matrix unchecked) ・無次元の実数演算(real selected && matrix unchecked) 次の2次の正方行列の行列積を一例に (0,0:0,1+i)(1,0:0,1) ・上記の用途順に演算結果のみ示す -> (0,0:0,1+i) -> (0,0:0,1) -> 1+i -> 1 用途によらず、行列要素は左から右にすべて演算する ・行vectorをcolon:区切りで列挙 (x=1,x=2x:x=2x,x) -> (0,0:0,4) ・列vectorをcolon:区切りで列挙 {x=1,x=2x:x=2x,x} -> (0,0:0,4) その上で、無次元の演算の場合、operandの最終要素を取り出して演算する (x=1,x=2x:x=2x,x)*1 || {x=1,x=2x:x=2x,x}*1 || (0,0:0,4)*1 || (4)*1 -> 4 ・よって行列の積は次の乗算に変換される (x=1,x=2x:x=2x,x){x=1,x=2x:x=2x,x} || (4)*{4} -> 16 以上より、n次の正方行列の行列積の演算量を用途順に概算して示す 4*(n*n)*(n*n) (n*n)*(n*n) 4 1 |
|
目次
real自動切替 |
real自動切替機能について記述する
Ver.2.184.44以降、real自動切替機能を追加 ・complex ⇒ auto-real selected既定 real自動切替機能の仕様を列挙する ・real判別方法:虚部が無次元の0(厳密等価) ・real判別対象:関数の引数vector||四則演算子のoperand test caseを列挙する eps -> 2.220446049250313e-16 MIN_VALUE -> 5e-324 1/0 -> Infinity 2**3 -> 8 2^3 -> 8 (2**3)i -> 8i (-1)**0.5 -> NaN (-1)^0.5 -> NaN sqrt(-1) -> NaN sqrt(2) -> 1.4142135623730951 sqrt(4) -> 2 sqrt(i) -> 0.7071067811865476+0.7071067811865475i pow(-1,0.5) -> NaN pow(2,2) -> 4 pow(2,4) -> 16 pow(i,4) -> 1-2.4492935982947064e-16i pow(2,i) -> 0.7692389013639721+0.6389612763136348i log(-1) -> NaN log(2) -> 0.6931471805599453 log(4) -> 1.3862943611198906 log(i) -> 1.5707963267948966i sqrt(-1+false*i) -> NaN sqrt(-1+eps*i) -> 6.123233995736766e-17+i sqrt(-1+MIN_VALUE*i) -> 6.123233995736766e-17+i pow(-1+(eps)i,0.5) -> 6.123233995736766e-17+i pow(-1+(MIN_VALUE)i,0.5) -> 6.123233995736766e-17+i log(-1+i*eps) -> 3.141592653589793i log(-1-i*eps) -> -3.141592653589793i pow(2+MIN_VALUE*i,3) -> 7.999999999999998 complex(2,false)**3 -> 7.999999999999998+O(2e-15) imag(NaN*(1+2i)) -> NaN 2.2%2 -> 0.20000000000000018 NaN&NaN -> 0 |
|
目次
拡張行列演算 |
拡張行列演算の演算仕様について記述する
Ver.2.73.29以降、本来、定義できない行列演算を拡張して拡張行列演算を定義する ・定義できない行列演算は実用しないため、拡張前の演算結果に影響なし ・Ver.2.74.29以降、演算子のoperandを追加で拡張 ・Ver.2.88.32以降、定義できない乗算||減算||加算を拡張対象に追加 詳細は拡張履歴参照 拡張行列演算の仕様を列挙する ・拡張対象:関数の引数vector||演算子のoperand ・再帰高階関数の反復処理より高速に演算可 ・行列関数||高階関数||高階行列関数は拡張対象外(変更なし) test caseを列挙する ・Hadamard積 (1,2,3)*(4,5,6) -> (4,10,18) ・実数演算 min(1,2:3,4) || (min(1,2):min(3,4)) -> (1:3) max(1,2:3,4) || (max(1,2):max(3,4)) -> (2:4) (2,3,4)^(1,2) || (2,3,4)^(1,2,2) -> (2,9,16) (2,3)**{1,2} || (2,3:2,3)**{1,2:1,2} || (2,3:2,3)**(1,1:2,2) -> (2,3:4,9) (1,2:3,4:5)**{1,2} || (1,2:3,4:5)**{1,2,2:1,2} || (1,2:3,4:5)**(1,1:2,2:2) -> (1,2:9,16:25) (3,5,7)%(1,5) || (3,5,7)%(1,5,5) -> (0,0,2) (1,2,4)/2 || (1,2,4)/(2,2,2) -> (0.5,1,2) 2/(1,2,4) || (2,2,2)/(1,2,4) -> (2,1,0.5) (1,2,4)2 || (1,2,4)*2 || (1,2,4)*(2,2,2) -> (2,4,8) (2,3)(1,2,4) || (2,3)*(1,2,4) || (2,3,3)*(1,2,4) -> (2,6,12) (1,2,4)-2 || (1,2,4)-(2,2,2) -> (-1,0,2) (2,3)+(1,2,4) || (2,3,3)+(1,2,4) -> (3,5,7) (2,3)=(1,2,4) || (2,3,3)=(1,2,4) || =(1,2,4)-(2,3,3) -> (-1,-1,1) clear; x=(2,3); x=(1,2,4); x -> (1,2,4) clear; x=(2,3); (1,2,4)=x || (1,2,4)=(2,3) || =(2,3,3)-(1,2,4) -> (1,1,-1) (2,4,8)>>(3,1) || (2,4,8)>>(3,1,1) -> (0,2,4) clear; (x={0,1,2,3,4,5,6,7})||~(x<<1)%3 -> (-1:-3:-2:-1:-3:-2:-1:-3) ・複素数演算 camin((1,2:3,4)i) || (camin(1i,2i):camin(3i,4i)) -> (1:3) camax((1,2:3,4)i) || (camax(1i,2i):camax(3i,4i)) -> (2:4) (5,3,1)/(2i,i) || (5,3,1)/(2i,i,i) -> (-2.5i,-3i,-i) clear; x={0,1,2,3,4,5,6,7}; y=(x*1,x*2,x*3)/(i,-2,3); y -> ( 0,0,0: -i,-1,1: -2i,-2,2: -3i,-3,3: -4i,-4,4: -5i,-5,5: -6i,-6,6: -7i,-7,7 ) min(y),max(y) -> (0,0:-1,1:-2,2:-3,3:-4,4:-5,5:-6,6:-7,7) clear; x={0,1,2,3,4,5,6,7}; N=sizer(x); f=e^((x*2*pi/N)i); f -> ( 1: 0.7071067811865476+0.7071067811865475i: 6.123233995736766e-17+i: -0.7071067811865475+0.7071067811865476i: -1+1.2246467991473532e-16i: -0.7071067811865477-0.7071067811865475i: -1.8369701987210297e-16-i: 0.7071067811865474-0.7071067811865477i ) round_real(f,n)=<round(real(f)*round(10**(n||1)))/round(10**(n||1)); round_imag(f,n)=<round(imag(f)*round(10**(n||1)))/round(10**(n||1)); round_f(f,nr,ni)=<round_real(=<f,nr)+(round_imag(=<f,ni))i; round_f(=<f,,2) -> (1:0.7+0.71i:i:-0.7+0.71i:-1:-0.7-0.71i:-i:0.7-0.71i) |
|
目次
型の種類 |
型の種類について記述する
演算単位として唯一定義する型、structureを次に示す ・浮動小数点数の実部と虚部から成る複素数の行列 演算単位のstructureを以降、単位tree構造と呼ぶ ・複素数や整数、文字列等の型は定義しない(必要に応じて変数名で区別する) ・変数名symbolのみ、call時に内部で判別する ・よって用途をseamlessに切替えて演算量を調整する 詳細は単位tree構造参照 |
|
目次
変数の種類 |
変数の種類について記述する
変数の種類は以下2種類で代入記号と読出し方法が異なる ・変数 ・式変数 |
|
目次
const宣言 |
const宣言について記述する
・Ver.2.741.109以降、memory確保の致命的な不具合を修正 式変数の式読出し:常に動的に確保 ⇒ const宣言の場合、静的に確保(useStaticScopes2dArray同様) $make_f=<[,=<()=<1]=>; _r(=<make_f(),,1e8) -> Ver.2.249.57以降、再代入と重複宣言を禁止するconst宣言を暫定追加($開始のbeta版) ・Ver.2.254.59以降、$let宣言の再代入の仕様変更(初回のみ、$あり ⇒ 常時、$あり) ・Ver.2.261.61以降、define判別idを追加して式変数のre-callに対応(再利用の場合、id削除) [$f=<0,$a=1,$b=2,=<(c)=<f=>+a+b+c]=>f,f(3)=>,f(4)=>,f(5)=> -> (0,6,7,8) f(c)=<[$f=<0,$a=1,$b=2,=<f=>+a+b+c]=>,f(3)=>,f(4)=>,f(5)=> -> ・Ver.2.262.61以降、式変数への式読出しに対応 [$f=<0,$a=1,$b=2,=<(c)=<f=>+a+b+c]=>$g,g=<1 -> [MyErr]Invalid SEe-scope-const(g) f(c)=<[$f=<0,$a=1,$b=2,=<f=>+a+b+c]=>$f,f(3)=> -> [MyErr]Invalid SEe-scope-existed(f) ・Ver.2.262.62以降、define判別idが消失する致命的な不具合を修正(value-id ⇒ name-id継承) clear; $a=-1; ((((a)=<(b)=<(a,b))|||false)(1)=>)(2)=> -> ・Ver.2.264.62以降、式変数の再利用に対応(id削除 ⇒ name-id保持) clear -> local storage cleared $x=-1; x -> -1 f(x)=<x; f(1)=> -> f(x)=<[=<x]=>; f(1)=> -> 1 clear -> local storage cleared $f=<-1; f=> -> -1 f(x)=<[=<x]=>; f(1)=> -> g(=<f)=<f=>; g(=<1)=> -> g(=<f)=<[=<f=>]=>; g(=<1)=> -> 1 ・scope参照 clear; $a=2; f(?a)=<a=3; f(?a) -> [MyErr]Invalid SEv-scope-const(a) clear; $a=2; f(?a)=<last[,a=3]; f(?a) -> [MyErr]Invalid SEv-scope-const(a) clear; $a=2; f(a)=<a=3; f(a) -> [MyErr]Invalid SEv-scope-const(a) clear; $a=2; f(a)=<last[,a=3]; f(a) -> 0 ・Ver.2.298.72~2.372.86以降、method演算子 clear; $A=(1,2:3,4); A.unshift(5); A -> [MyErr]Invalid const var(A.unshift) clear; $A=(1,2:3,4); A.push(5); A -> [MyErr]Invalid const var(A.push) clear; $A=(1,2:3,4); A.shift(); A -> [MyErr]Invalid const var(A.shift) clear; $A=(1,2:3,4); A.pop(); A -> [MyErr]Invalid const var(A.pop) clear; $A=(1,2:3,4); A.flip(); A -> [MyErr]Invalid const var(A.flip) $const宣言($開始のbeta版) ・変数 clear; $a=1; a -> 1 ・行列要素pattern matchingはlet宣言 clear; a=1; ($a)=2; a -> 2 clear; ($a)=2; a=1; a -> 1 clear; ($a)=2; $a=1; a -> [MyErr]Invalid SEv-scope-existed(a) clear; $a=1; a=2; a -> [MyErr]Invalid SEv-scope-const(a) clear; $a=-1; a=-2; a -> [MyErr]Invalid SEv-scope-const(a) clear; $a=1; ($a)=2; a -> [MyErr]Invalid SEv-scope-const(a) clear; a=1; $a=2; a -> [MyErr]Invalid SEv-scope-existed(a) clear; ($a)=1; $a=2; a -> [MyErr]Invalid SEv-scope-existed(a) clear; $a=1; $a=2; a -> [MyErr]Invalid SEv-scope-duplicate(a) clear; ($a=0,[$a=1,[$a=2,[$a=3,a],a],a],a) -> (0,0,0,0,3,2,1,0) ・式変数のargumentsはlet宣言 clear; $n=1; f(n)=<(n,n); f(1),f(2) -> [MyErr]Invalid SEv-scope-const(n) clear; $n=1; f(m)=<(m=2,m); f(n),f(n) -> (0,2,0,2) ・単独scope clear; $n=1; f(n)=<[n,n]; f(1),f(2) -> (1,1,2,2) ・dummy変数はlet宣言 clear; _s((n)=<n+1,1,3) -> 9 clear; _s((n)=<n+1,1,3); $n=1; n -> 1 clear; n=1; _s((n)=<n+1,n,3) -> 9 ・scope変数の宣言と干渉あり仕様 clear; $n=1; _s((n)=<n+1,n,3) -> [MyErr]Invalid SEv-scope-const(n) clear; _s((n)=<n+1,1,3); $n=1; n -> 1 ・式変数 clear; $f=<1; f -> 1 clear; $f=<1; f=<2; f -> [MyErr]Invalid SEe-scope-const(f) clear; f=<1; $f=<2; f -> [MyErr]Invalid SEe-scope-existed(f) clear; $f=<1; $f=<2; f -> [MyErr]Invalid SEe-scope-duplicate(f) clear; ($f=<0,[$f=<1,[$f=<2,[$f=<3,f],f],f],f) -> (0,0,0,0,3,2,1,0) $let宣言($開始のbeta版) ・変数 clear; a=1; a -> 1 ・行列要素pattern matchingはlet宣言 clear; $a=1; ($a)=2; a -> 2 ・Ver.2.254.59以降、$let宣言の再代入の仕様変更(初回のみ、$あり ⇒ 常時、$あり) clear; ($a)=2; a=1; a -> clear; ($a)=2; $a=1; a -> clear; a=1; $a=2; a -> [MyErr]Invalid SEv-scope-const(a) clear; a=-1; $a=-2; a -> [MyErr]Invalid SEv-scope-const(a) clear; a=1; ($a)=2; a -> [MyErr]Invalid SEv-scope-const(a) clear; a=1; a=2; a -> [MyErr]Invalid SEv-scope- clear; $a=1; $a=2; a -> clear; $a=1; a=2; a -> clear; ($a)=1; a=2; a -> clear; (a=0,[a=1,[a=2,[a=3,a],a],a],a) -> (0,0,0,0,3,2,1,0) ・式変数のargumentsはlet宣言 clear; n=1; f(n)=<(n,n); f(1),f(2) -> [MyErr]Invalid SEv-scope-const(n) clear; n=1; f(m)=<(m=2,m); f(n),f(n) -> clear; n=1; f(m)=<($m=2,m); f(n),f(n) -> (0,2,0,2) ・単独scope clear; n=1; f(n)=<[n,n]; f(1),f(2) -> (1,1,2,2) ・dummy変数はlet宣言 clear; _s((n)=<n+1,1,3) -> 9 clear; _s((n)=<n+1,1,3); n=1; n -> 1 clear; $n=1; _s((n)=<n+1,n,3) -> 9 ・scope変数の宣言と干渉あり仕様 clear; n=1; _s((n)=<n+1,n,3) -> [MyErr]Invalid SEv-scope-const(n) clear; _s((n)=<n+1,1,3); n=1; n -> 1 ・式変数 clear; f=<1; f -> 1 clear; f=<1; $f=<2; f -> [MyErr]Invalid SEe-scope-const(f) clear; f=<1; f=<2; f -> [MyErr]Invalid SEe-scope- clear; $f=<1; $f=<2; f -> clear; $f=<1; f=<2; f -> clear; (f=<0,[f=<1,[f=<2,[f=<3,f],f],f],f) -> (0,0,0,0,3,2,1,0) 留意事項を列挙する ・変数の場合、参照ではなく、行列iterableのconst宣言として定義する clear; $A=(1,2:3,4); A[1][1]=-1; A -> [MyErr]Invalid SEv-scope-const(A) clear; $A=(1,2:3,4); A.push(5); A -> [MyErr]Invalid const var(A.push) |
|
目次
変数のscope |
変数のscopeについて記述する
・変数毎にstorageを共有する ・高階関数||高階行列関数のdummy変数のみ、scopeが独立する 次の命令文の組合せで完全独立のlocal scopeを代替可 ・comment文を使用 x=2; store; clear; x=3/*independent local scope*/; restore; x -> 2 Ver.2.31.17以降、角括弧[]に変数のscopeを追加 ・Nativeのvar宣言の場合、関数宣言に紐付くfunction-scope(useScopeWith参照)に対して ・let||const宣言同様に、括弧に紐付くblock-scopeとして扱う ・scope不定の式変数のargumentsを削除する等、closure機能が異なる ・Ver.2.229.56以降、式変数のargumentsをscope変数から削除しない仕様に変更 ・Ver.2.290.71以降、式変数のargumentsのscope変数保持条件の仕様変更 保持条件:無条件 ⇒ 式変数が未解決(右代入を含む) ・Ver.2.291.71以降、scope変数のsearch-precedenceの仕様変更 特徴を列挙する ・直列scope内の変数・式変数はreadonly(pollution disabled) ・block-scope範囲の可読性を優先(block単位の角括弧[]内と対応) ・単独scopeを意識する負担あり ・static scopes2d arrayを共有するため、複数の状態を保持不可(new演算子は未実装) Ver.2.213.47以降、function-scopeに変更する場合、useScope||useScopeWith||内部option参照 |
|
目次
参照透過性 |
参照透過性について記述する
原則、参照透過性あり:実装関数の引数||式渡しが同値||同義の場合、常に同じ結果を返す scope変数を参照する実装関数を列挙する ・Jacobi高階行列関数 scope変数を参照、上書きする実装関数を列挙する ・Newton高階行列関数||solvex_iteration||solveAinv||solvex_non_linear ・ODE高階行列関数||explicit ODE_RK4 ・微分高階関数 暫定対策を列挙する ・local変数を追加/削除するadd/del最上位関数 ・Ver.2.222.50以降、命令文を拡張 ・Ver.2.225.53以降、高階関数||高階行列関数のdummy変数がscope変数に残存する不具合を修正 ・Ver.2.226.56以降、iterator演算子のdummy変数がscope変数に残存する不具合を修正 ・Ver.2.229.56以降、式変数のargumentsをscope変数から削除しない仕様に変更 上書き不可の仕様を維持(再帰callの参照透過性を維持) ・Ver.2.231.56以降、高階関数||高階行列関数の対策を実施 dummy変数の変数名symbol:関数名の一部 ⇒ 関数の引数(Ver.2.812.131以降、旧仕様廃止) ・Ver.2.234.56以降、高階関数||高階行列関数の対策を完了 scope変数を参照、上書きする ⇒ scope変数から独立する(引数のみ有効) ・Ver.2.857.158以降、微分高階関数の対策を完了 scope変数を参照する ⇒ scope変数から独立する(引数のみ有効) ・以上より、Ver.2.835.141~2.857.159以降、高階関数||高階行列関数の関連項目を一括削除 |
|
目次
storage |
storageについて記述する
・Ver.2.139.36以降、global storageの初期化処理を修正(初回のClear実行でerror発生時の対策) storageは変数・式変数を別々に保存するobjectで次の3種類 ・local storage ・global storage ・local buffer local storage ・演算実行確定1回の各実行文の変数・式変数を保存する ・保存された変数をlocal変数と呼ぶ global storage ・演算実行確定1回毎に返る変数・式変数を累積保存する ・保存された変数をglobal変数と呼ぶ local buffer ・local storageを一時的に記憶する ・演算実行確定1回毎に初期化する 演算実行確定1回のstorageのflowを示す ・演算実行開始 global storage ⇒ local storageに復帰 ・演算実行途中 local storageのread-write ⇔ local buffer ・演算実行終了 local storage ⇒ global storageに保存 Ver.2.31.17以降、static scopes2d arrayを追加 ・保存された変数をscope変数と呼ぶ ・scope変数(local storageを除く)は演算実行確定1回毎に初期化 Ver.2.32.17以降、scope付式変数の再利用に対応 ・演算実行開始で式変数の復帰時、scope-idsを更新 |
|
目次
階層とscope の関係 |
階層とscopeの関係について記述する
・Ver.2.195.46以降、追記 parse段階で括弧のnestingによる構文を解析し、深さ方向にtree構造を階層化する ・Ver.2.228.56以降、式渡しも同様に、括弧に変換して階層化 ・深さ0の0階層にlocal storageを統合・共通化する(命令文を含む) ・既定で角括弧[]のみ変数のscopeを使用する ・0階層を除く階層は実行文毎に独立する ・0階層を最上位の階層とする ・0階層から階層の深さを昇順に定義する ・以上より、階層の概念を次に示す 実行文A[,]; 実行文B[,[],[],[,[,[,]]]]; -> 0階層[A-1階層,]; 0階層[B-1階層,[B-2階層並列1],[B-2階層並列2],[B-2階層並列3,[B-3階層直列,[B-4階層直列,]]]]; 定義を列挙する ・階層毎に並列に並んだscopeは互いに独立で、並列scopeと定義する ・階層の深さ方向に直列に並んだscopeを直列scopeと定義する ・自身の階層以上(深さの降順)の直列scopeは参照可能(readonly)で、直列scope内と定義する ・それ以外の参照できないscopeを直列scope外と定義する ・同じ階層の並列scopeは直列scope外に含む ・よって0階層のlocal storageはすべてのscopeの直列scope内で共通化される ・以上より、parse段階で作るscopeの配列をstatic scopes2d arrayと定義する |
|
目次
search- precedence |
scope変数のsearch-precedenceについて記述する
階層の概念 実行文A[,]; 実行文B[,[],[],[,[,[,]]]]; -> 0階層[A-1階層,]; 0階層[B-1階層,[B-2階層並列1],[B-2階層並列2],[B-2階層並列3,[B-3階層直列,[B-4階層直列,]]]]; 直列scope内変数のsearch-precedenceの一例 ・上記B-2階層並列1の場合、次の論理ORを短絡評価 B-2階層並列1 || B-1階層 || 0階層 ・上記B-3階層直列の場合、次の論理ORを短絡評価 B-3階層直列 || B-2階層並列3 || B-1階層 || 0階層 ・上記B-4階層直列の場合、次の論理ORを短絡評価 B-4階層直列 || B-3階層直列 || B-2階層並列3 || B-1階層 || 0階層 ・よって直列scope内の階層(深さの降順)で0階層(local storage)が最下位のprecedence 変数・式変数のsearch-precedence ・変数を式変数より優先 ・Ver.2.291.71以降、useMutexとともに仕様変更 変数||式変数のsearch-precedence:全階層 ⇒ 階層毎 clear; f=<-1; f=1; [f=2,=<f]=>,[f=<-2,=<f]=> -> (2, |
|
目次
scope継承 |
scope継承について記述する
・Ver.2.31.17以降、式変数のscope継承callを追加 ・Ver.2.219.50以降、式変数のscope継承passを追加 留意事項を列挙する ・scope継承はcall時に実施(式代入の継承を含む) ・高階関数||高階行列関数の式渡しは非対応(対応予定なし) |
|
目次
scope参照 |
scope参照について記述する
・Ver.2.303.73以降、scope変数のscope参照の仕様追加 参照渡し記号:?symbol ・Ver.2.303.74以降、行列への参照を適用する参照渡しの不具合を修正 clear; f(?a)=<a[0][0]=2; a=1,a,f(?a),a -> ・Ver.2.304.76以降、再利用の不具合を修正 clear; A=1,f(?A)=<A=3,[A=2,f(?A),A]; A=4; A -> clear; g=<1,f(?g)=<g=<3,[g=<2,f(?g),g()]; g=<4; g() -> ・Ver.2.343.83以降、変数の代入時に右辺のscope参照を削除する仕様に修正 clear; arr=(1,2),f=(?arr)=<[arr1=arr,arr1[][1]=-1],f(?arr)=>; arr -> clear; arr=(1,2),f=(?arr)=<[arr1=arr,arr1[][1]=-1,arr=arr1],f(?arr)=>; arr -> clear; arr=(1,2),f=(?arr)=<[arr1=arr+0,arr1[][1]=-1,arr=arr1],f(?arr)=>; arr -> (1,-1) ・Ver.2.346.85以降、行列要素pattern matchingも同様に修正 clear; arr=(1,2),f=(?arr)=<[($arr1)=(=<arr),arr1[][1]=-1,],f(?arr)=>; arr -> clear; arr=(1,2),f=(?arr)=<[($arr1)=(=<arr),arr1[][1]=-1,arr=arr1],f(?arr)=>; arr -> 留意事項を列挙する ・Ver.2.343.83以降、改善するが、右代入の併用困難(Call-by-Reference参照) ・読出し時に参照を不使用のため、意図とは異なる可能性あり(現状、代入時のみ参照を使用) ・scope変数未定義の場合、error終了 clear; a=1,f(?a)=<a=2,a,f(?a),a -> (0,0,1,0,2) clear; f(?a)=<a=2,f(?a),a -> [MyErr]Undef scope-var(a) clear; a=1,[f(?a)=<a=2,a,f(?a),a] -> [MyErr]Undef scope-var(a) |
|
目次
用語集 |
用語を整理する
・static scopes2d array:全scopeの変数・式変数の集合 ・直列scope内変数:直列scope内の変数・式変数の集合 ・直列scope内self変数:self-idsの変数・式変数(static scopes2d arrayの単位要素) ・scope変数:直列scope内self変数(式変数のargumentsの保存先||dummy変数のbuffer) ・local storage:static scopes2d arrayの0階層に共通化 ・local変数:local storageの変数・式変数 ・global変数:global storageの変数・式変数 |
|
目次
plot2d 出力仕様 |
Graphing Calculator's plot2dの出力仕様について記述する
plot2dの演算は高速化のため、誤差を評価しない・logを作らない ・誤差を含めたlogを作る場合、別途、通常の演算が必要 ・Ver.2.224.51以降、変数名symbol残存時のerror処理を追加(logを作る場合、log作成中に検出) csv/history-txt出力のplot2d-command-logとplot2d-options-logについて記述する ・整合性保証のため、plot2dの演算実行確定時のlogを表示する ・よって演算終了後に変更した現在のzをlogに残す場合、再演算が必要 ・Ver.2.843.152以降、v入力欄を含むhistory-txt出力の不具合を修正(log出力無効 ⇒ 有効) semi-colon;区切りで行列の最終要素の数値をgraphに描画する ・命令文||代入文||空行列のみを各軸に入力した場合、0を返して描画する ・処理を列挙する場合、最終列挙の要素が最終要素とは限らない点、留意が必要 詳細はlast行列関数参照 媒介変数tの区間[t0,t1]のlocal storageは独立 ・global storageをreadonlyで共有する場合、shared storage checked x軸とy軸のlocal storageはx軸優先で共通 ・global storageをreadonlyで共有する場合、shared storage checked t0/t1の演算を実行後、x/yの演算を実行 ・t0/t1の演算はSingle-thread実行で中断不可 ・x/yの演算はMulti-thread実行を選択可 Ver.2.162.39以降、NaNを含む演算結果の描画に対応 ・NaN要素のmarker出力を省略 ・NaN要素へのline出力を省略 ・全要素がNaNの場合、error終了(plot範囲の初期化失敗) [MyErr]Invalid plot2d isInf ・非対応の機能を列挙する ・string-path ・svg出力(marker||line出力の標準機能を除く) svg出力機能について記述する ・canvas-globalCompositeOperation無効(source-over) ・既定markerのdestination-outは背景色source-overで代替(透明の場合、白) ・canvas描画処理の継承互換性のため、group化等による最適化はしない ・z入力欄から入力不可のsemi-colon;等の特殊文字を直接file編集可 ・その他、font-family等も直接file編集可 |
|
目次
plot2d -command 入力仕様 |
Graphing Calculator's plot2d-commandの入力仕様について記述する
以下2種類のplot2d-commandは操作panel中段のtext入力欄から実行する plot2d("t0","t1","xt","yt") || plot2d(""t0"",""t1"",""xt"",""yt"") Ver.2.843.151以降、仕様訂正 plot2d(xt,yt) plot2d{xt,yt} Ver.2.175.42以降、追加 ・plot2d-command最優先で他の実行文は破棄other sentences ignored ・plot-button実行中の割込み不可 |
|
目次
plot2d -from-log 入力仕様 |
plot2d-from-logの入力仕様について記述する
csv/history-txtに記録されるlogからplot2d-commandを実行する ・Ver.2.175.42~2.176.44以降、実行後、空白文字が消失する不具合を修正 ・Ver.2.810.131以降、更新箇所 ・Ver.2.843.151以降、plot2d-from-logの区切り文字とdot演算子の記号衝突を訂正 tokenの区切り文字:' ⇒ ["]{1,2} plot2d-from-logのformatを次に示す plot2d("t0","t1","xt","yt") || plot2d(""t0"",""t1"",""xt"",""yt"") plot2d("t0","t1","xt","yt","N") || plot2d(""t0"",""t1"",""xt"",""yt"",""N"") plot2d("t0","t1","xt","yt","N","z") || plot2d(""t0"",""t1"",""xt"",""yt"",""N"",""z"") ・Ver.2.837.145以降、改行文字に対応(line commentを含む場合、実行不能を修正) plot2d("t0","t1","xt // line comment ","yt","N","z") ・Ver.2.25.12以降、第5引数Nにsingle quotation mark(tokenの区切り文字)を付与 ・Ver.2.27.14以降、第6引数zとcomment文入力に対応 Ver.2.837.145以降、改行文字に対応 ・plot2d-commandの一例を示す plot2d("-5","5","t;","SND(t)=<exp(-t^2/2)/sqrt(2pi),SND(t);") plot2d("-5","5","t;","SND(t)=<exp(-t^2/2)/sqrt(2pi),SND(t);","50") plot2d("-5","5","t;","SND(t)=<exp(-t^2/2)/sqrt(2pi),SND(t);","50","circle") Ver.2.843.150以降、v入力欄をcommandに追加 plot2d("-5","5","t;","SND(t)=<exp(-t^2/2)/sqrt(2pi),SND(t);","50","circle","","","") ・N入力値は ・comment文入力の一例を示す plot2d("1e-3(1+i)/*t0*/","1e2(1+i)/*t1*/","x=t,x/*xt*/;","x;2x;3x;4x;5x;6x;7x;8x;9x;10x/*yt*/;","10","circle/*marker*/;") plot2d("1e-3(1+i)/*t0*/","1e2(1+i)/*t1*/","x=t,x // xt ;","x;2x;3x;4x;5x;6x;7x;8x;9x;10x/*yt*/;","10","circle/*marker*/;") ・Ver.2.837.145以降、plot終了のlog表示を追加 -> plot2d-from-log finished |
|
目次
plot2d -from-arr 入力仕様 |
plot2d-from-arrの入力仕様について記述する
任意の時系列dataからplot2d-commandを実行する ・Ver.2.129.35以降、各(x,y)の行sizeを独立化 csv出力時、欠損要素=undefined svg出力時、欠損要素=NaN ・Ver.2.175.42~2.175.43以降、欠損要素のNaN変換不具合(一部legendが消失)を修正 plot2d-from-arrのformatを次に示す ・引数が列vectorの場合 plot2d(x(t)変数名symbol,y(t)変数名symbol) ・Ver.2.175.42以降、引数が行vectorの場合 plot2d{x(t)変数名symbol,y(t)変数名symbol} ・xt,ytの場合 plot2d(xt,yt) plot2d{xt,yt} ・Ver.2.175.42以降、括弧内の plot2d(xt, yt) plot2d{xt, yt} ・Ver.2.837.145以降、改行文字に対応 plot2d(xt, yt) plot2d{xt, yt} ・plot終了のlog表示 -> plot2d-from-arr finished ・circleを描く時系列data作成の一例を示す ・式変数の式読出し記号=>を省略する場合、変数名の重複に留意する clear; t0=0; t1=2pi; tn=<t0+(t1-t0)n/N; N=10; /*init=<last{xt=zeros(N+1,1),yt=zeros(N+1,1)};*/ init=<last{xt=vectorc(N+1),yt=vectorc(N+1)}; stepn=<last{xt[n]=cos(tn),yt[n]=sin(tn)}; evolutionN=<_sn(=<stepn,0,N); init; evolutionN; xt,yt -> ・strict-modeの場合 clear; t0=0; t1=2*pi; tn=<t0+(t1-t0)*n/N; N=10; /*init=<last{xt=zeros(N+1,1),yt=zeros(N+1,1)};*/ init=<last{xt=vectorc(N+1),yt=vectorc(N+1)}; ・Ver.2.203.46以降、変数への式読出しの仕様廃止 stepn=<last{tn=tn=>,xt[n]=cos(tn),yt[n]=sin(tn)}; /*evolutionN=<_sn(=<{stepn=>},0,N);*/ evolutionN=<_sn(=<stepn,0,N); init=>; evolutionN=>; xt,yt -> ( 1,0: 0.8090169943749475,0.5877852522924731: 0.30901699437494745,0.9510565162951535: -0.3090169943749471,0.9510565162951536: -0.8090169943749473,0.5877852522924732: -1,1.2246467991473532e-16: -0.8090169943749478,-0.5877852522924727: -0.30901699437494756,-0.9510565162951535: 0.30901699437494723,-0.9510565162951536: 0.8090169943749473,-0.5877852522924734: 1,-2.4492935982947064e-16 ) 複数の時系列dataを作成してplot2d-commandを実行する一例を以下に示す ・上記xt,ytの元dataを結合して作る場合 xt4=(xt*0,xt*1,xt*2,xt*3); yt4=(yt*0,yt*1,yt*2,yt*3); plot2d(xt4,yt4) ・同義 xt4=xt*(0,1,2,3); xt4 -> ( 0,1,2,3: 0,0.8090169943749475,1.618033988749895,2.4270509831248424: 0,0.30901699437494745,0.6180339887498949,0.9270509831248424: 0,-0.3090169943749471,-0.6180339887498942,-0.9270509831248414: 0,-0.8090169943749473,-1.6180339887498947,-2.427050983124842: 0,-1,-2,-3: 0,-0.8090169943749478,-1.6180339887498956,-2.4270509831248432: 0,-0.30901699437494756,-0.6180339887498951,-0.9270509831248427: 0,0.30901699437494723,0.6180339887498945,0.9270509831248417: 0,0.8090169943749473,1.6180339887498947,2.427050983124842: 0,1,2,3 ) yt4=yt*(0,1,2,3); yt4 -> ( 0,0,0,0: 0,0.5877852522924731,1.1755705045849463,1.7633557568774194: 0,0.9510565162951535,1.902113032590307,2.8531695488854605: 0,0.9510565162951536,1.9021130325903073,2.853169548885461: 0,0.5877852522924732,1.1755705045849465,1.7633557568774196: 0,1.2246467991473532e-16,2.4492935982947064e-16,3.6739403974420594e-16: 0,-0.5877852522924727,-1.1755705045849454,-1.763355756877418: 0,-0.9510565162951535,-1.902113032590307,-2.8531695488854605: 0,-0.9510565162951536,-1.9021130325903073,-2.853169548885461: 0,-0.5877852522924734,-1.1755705045849467,-1.76335575687742: 0,-2.4492935982947064e-16,-4.898587196589413e-16,-7.347880794884119e-16 ) ・case違いの演算を繰り返してxt,ytを作り直す場合 ・strict-modeの場合 clear; t0=0; t1=2*pi; tn=<t0+(t1-t0)*n/N; N=10; M=3; init=<last{xt=zeros(N+1,M+1),yt=zeros(N+1,M+1)}; ・Ver.2.203.46以降、変数への式読出しの仕様廃止 stepnm=<last{tn=tn=>,xt[n][m]=cos(tn)*m,yt[n][m]=sin(tn)*m}; casesM=<_sm(=<stepnm,0,M); evolutionN=<_sn(=<casesM,0,N); init=>; evolutionN=>; xt4=xt; xt4 -> ( 0,1,2,3: 0,0.8090169943749475,1.618033988749895,2.4270509831248424: 0,0.30901699437494745,0.6180339887498949,0.9270509831248424: 0,-0.3090169943749471,-0.6180339887498942,-0.9270509831248414: 0,-0.8090169943749473,-1.6180339887498947,-2.427050983124842: 0,-1,-2,-3: 0,-0.8090169943749478,-1.6180339887498956,-2.4270509831248432: 0,-0.30901699437494756,-0.6180339887498951,-0.9270509831248427: 0,0.30901699437494723,0.6180339887498945,0.9270509831248417: 0,0.8090169943749473,1.6180339887498947,2.427050983124842: 0,1,2,3 ) yt4=yt; yt4 -> ( 0,0,0,0: 0,0.5877852522924731,1.1755705045849463,1.7633557568774194: 0,0.9510565162951535,1.902113032590307,2.8531695488854605: 0,0.9510565162951536,1.9021130325903073,2.853169548885461: 0,0.5877852522924732,1.1755705045849465,1.7633557568774196: 0,1.2246467991473532e-16,2.4492935982947064e-16,3.6739403974420594e-16: 0,-0.5877852522924727,-1.1755705045849454,-1.763355756877418: 0,-0.9510565162951535,-1.902113032590307,-2.8531695488854605: 0,-0.9510565162951536,-1.9021130325903073,-2.853169548885461: 0,-0.5877852522924734,-1.1755705045849467,-1.76335575687742: 0,-2.4492935982947064e-16,-4.898587196589413e-16,-7.347880794884119e-16 ) 斜方投射の時系列dataを作成する一例を以下に示す ・total時間積分回数がplot2d-buttonのN回に対して1回で済むため、圧倒的に速い ・時間刻みを次の式変数dtnで定義してevolutionNで時間発展する dtn=<switch(n<=0,0:1,dt); ・strict-modeの場合 clear; g=-9.8; z_a=0+g*i; z_v0=20+20i; z_x0=0; dt=0.5; m=1; kCdA_sphere=1; x=<{z_x,z_v}; x_initial=<{z_x0,z_v0}; f=<{z_v,z_a-(kCdA_sphere/m)*z_v}; /*{$z_x,$z_v}=x_initial=>;*/ t0=0; t1=5; N=round((t1-t0)/dt); init=<last{xt=vectorc(N+1),yt=vectorc(N+1)}; dtn=<switch(n<=0,0:1,dt); step=<{x_next=_otdummy(=<f,=<x,=<x_initial,0,dtn=>)}; stepn=<last{step=>,xt[n]=real(z_x),yt[n]=imag(z_x)}; evolutionN=<_sn(=<stepn,0,N); init=>; evolutionN=>; xt,yt -> ( 0,0: 7.864583333333332+O(6e-2),6.818229166666667: 12.636583116319443+O(6e-2),9.028508843315972: 15.532093401308412+O(6e-2),8.442819167949535: 17.289004589856408+O(6e-2),6.160616838886046: 18.355047055824333+O(6e-2),2.849020113178252: 19.001890531268412+O(6e-2),-1.0871831084100707: 19.394376285899845+O(6e-2),-5.402379334009235: 19.63252519430902+O(6e-2),-9.947537460479563: 19.77702700592188+O(6e-2),-14.6322297611764: 19.86470649057239+O(6e-2),-19.40158732904714 ) ・斜方投射の各時刻の位置z_xの近似解に一致する xt+yt*i -> ( 0: 7.864583333333332+6.818229166666667i+O(6e-2): 12.636583116319443+9.028508843315972i+O(6e-2): 15.532093401308412+8.442819167949535i+O(6e-2): 17.289004589856408+6.160616838886046i+O(6e-2): 18.355047055824333+2.849020113178252i+O(6e-2): 19.001890531268412-1.0871831084100707i+O(6e-2): 19.394376285899845-5.402379334009235i+O(6e-2): 19.63252519430902-9.947537460479563i+O(6e-2): 19.77702700592188-14.6322297611764i+O(6e-2): 19.86470649057239-19.40158732904714i+O(6e-2) ) 大規模csvの時系列dataを入力する場合、csv-format参照 |
|
目次
csv-format 入力仕様 |
csv-formatの入力仕様と付随する留意事項について記述する
・Ver.2.142.36以降、実数値の大規模csv入力に対応 ・Ver.2.143.36以降、括弧なしのformatに対応 次の不具合を回避するため、parse段階で単位tree構造のarrに変換する Maximum call stack size exceeded Out of Memory ・Ver.2.140.36以降、演算実行のcancel-buttonを追加 ・Ver.2.144.36以降、operation段階の行列結合を含むdepthMax制限を追加(browser crashの2重対策) 実数値以外を含む大規模csv -> [MyErr]Nesting depthMax over ・Ver.2.156.38以降、行列結合の最適化を実施 csv-formatを次に示す 実数値,実数値,...,実数値 ・formatの適用範囲 {実数値,実数値,...,実数値} (実数値,実数値,...,実数値) [実数値,実数値,...,実数値] ・Ver.2.151.38以降、-0入力に対応 実数値 -0 -> -0 test caseを示す 0,1,2,3,4,5,6,7,8,9; xt=ans; xt -> (0,1,2,3,4,5,6,7,8,9) 0,1,2,3,4,5,6,7,8,9; xt=trans(ans); xt -> (0:1:2:3:4:5:6:7:8:9) xt={0,1,2,3,4,5,6,7,8,9}; xt -> (0:1:2:3:4:5:6:7:8:9) xt=(0,1,2,3,4,5,6,7,8,9); xt -> (0,1,2,3,4,5,6,7,8,9) xt=[0,1,2,3,4,5,6,7,8,9]; xt -> (0,1,2,3,4,5,6,7,8,9) xt=trans(0,1,2,3,4,5,6,7,8,9); xt -> (0:1:2:3:4:5:6:7:8:9) ・複素数vectorに変換する場合 zr={0,1,2,3}; zi={0,1,2,3}; z=zr+(zi)i; z -> (0:1+i:2+2i:3+3i) ・前置単項の符号を含む場合 zr={0,1,2,3}; zi={-0,-1,-2,-3}; z=zr+(zi)i; z -> (0:1-i:2-2i:3-3i) ・operand記号を含む場合 xt={+0.0,-1e-1,+2.2e+2,-012.345e+6,0xff,0x00}; xt -> (0:-0.1:220:-12345000:255:0) xt={+0.0,-1e-1,+2.2e+2,-012.345e+6,+0xff,-0x00}; xt -> (0:-0.1:220:-12345000:255:0) ・欠損要素は0 ,1, -> (0,1,0) (,,,) -> (0,0,0,0) [(,,,)] -> (0,0,0,0) ((,,,)) -> (0,0,0,0) {(,,,)} -> (0,0,0,0) xt={,,,}; {xt} -> (0:0:0:0) xt={,,,}; (xt) -> (0:0:0:0) xt={,,,}; [xt] -> (0:0:0:0) ・comma以外で列挙の場合、判別不可 (1,2,3:) -> (1,2,3:0,0,0) (1,2,3:,,) -> (1,2,3:0,0,0) x0=(1,2,3); x1=(,,); (x0:x1) -> (1,2,3:0,0,0) ・多重列挙の場合 (,,(1,2,3),,(,,(4,5,6),,),,) -> (0,0,1,2,3,0,0,0,4,5,6,0,0,0,0) ・実数値以外を含む場合 (,,(1,2,3),,(,,(4i,5,6),,),,) -> (0,0,1,2,3,0,0,0,4i,5,6,0,0,0,0) (,,(1,2,3),,(,,(z=i,5z,6),,),,) -> (0,0,1,2,3,0,0,0,0,5i,6,0,0,0,0) 留意事項を列挙する ・csv要素は実数値のみ対応 ・任意の要素数の時系列dataを入力可(初期化行列関数のmatSizeMax制限とは無関係) ・全要素が実数値の場合、括弧内の要素数上限=Order(10000) ・要素が実数値以外を含む場合、括弧内の要素数上限=Order( Ver.2.156.38以降、operation段階で行列結合のnestingを削減する最適化を実施 |
|
目次
white spaces 入力仕様 |
white spacesの入力仕様と付随する留意事項について記述する
以下のwhite spacesはparse段階で除去する ・空白文字 ・改行文字 |
|
目次
comment文 入力仕様 |
comment文の入力仕様と付随する留意事項について記述する
次のcomment文2種類は実行文に含まれない // line comment /* block comment */ test caseを示す x=-0xff; /*16進数literal*/ x>>3 // 右shift3回 -> -32 ・parse後の実行文を示す x=-0xff; x>>3 -> -32 ・同義 x=-255; floor(x*0.5*0.5*0.5) -> -32 ・Ver.2.87.32以降、int関数は0側に丸める x=-255; int(x*0.5*0.5*0.5) -> -31 留意事項を列挙する ・block commentのnesting不可(Native同様) /*/**/*/ -> [MyErr]Invalid operation */ clear;// /* */1 2 -> clear;2*/*//2*/ 3/*4*/ -> |
|
目次
命令文 入力仕様 |
命令文の入力仕様と付随する留意事項について記述する
命令文は最上位の実行文に相当する ・semi-colon;以外で区切った場合、error終了 clear || clear; -> local storage cleared clear, || clear: -> [MyErr]Invalid clear called ・括弧の中からcallの場合、error終了 (clear) || {clear} -> [MyErr]Invalid clear called ・変数への代入不可 clear; x=clear -> [MyErr]Invalid clear called ・式変数への式代入不可 f=<clear -> [MyErr]Invalid clear called 命令文を以下に示す clear ・call時点までの ・Ver.2.226.54以降、local storageがscope変数に残存する致命的な不具合を修正(後方互換性を復帰) x=3; x -> 3 clear -> local storage cleared x -> 3 clear; x -> [MyErr]Invalid REv(x) x -> 3 clear; ans -> [MyErr]Invalid REv(ans) ans -> 3 ・続けてglobal storageをclearする場合 Clear実行確定 -> storage cleared x -> [MyErr]Invalid REv(x) ans -> [MyErr]Invalid REv(ans) ・global storageに一切の変数を残さない場合 x=3; y=3x; y; clear -> local storage cleared x -> [MyErr]Invalid REv(x) y -> [MyErr]Invalid REv(y) ans -> [MyErr]Invalid REv(ans) store ・call時点までの ・deep-copyで新規複製 restore ・local bufferに保存された ・ clear; x=2; store; x=3; restore; x -> 2 clear; x=2; store; clear; restore; x -> 2 Ver.2.30.17以降、deep-copyで復帰(再利用に対応) clear; a=2; store; a=3; restore; a; a=3; restore; a -> 2 clear; a=2; store; a=3; restore; a; a=3; b=4; restore; b -> [MyErr]Invalid REv(b) ・HTML5描画canvas等、stack方式と異なり、最新のstore時点のobjectのみ再利用可 clear; a=2; store; a=3; store; restore; a; a=4; restore; a // not stacked -> 3 ・store~restore間に新規に定義された変数・式変数は参照不可 clear; x=2; store; y=3; clear; restore; x+y -> [MyErr]Invalid binary operation clear; x=2; store; y=3; store; clear; restore; x+y -> 5 ・store;clear~restore間の変数のscopeは完全独立 clear; x=2; store; clear; x=3; restore; x -> 2 clear; x=2; store; clear; x -> [MyErr]Invalid REv(x) ・local bufferは演算実行確定1回毎に初期化 storage cleared restore -> null buffer x=2; store -> local storage stored restore -> null buffer restore; x -> [MyErr]Invalid REv(x) stop ・call時点以降、演算を中断する x=3; 3x; stop; x -> operation stopped 留意事項を列挙する ・static scopes2d arrayのscope変数(local storageを除く)は演算実行確定1回毎に初期化 |
|
目次
区切り文字 入力仕様 |
区切り文字の入力仕様と付随する留意事項について記述する
区切り文字を優先順に列挙する ・実行文を区切るsemi-colon; 実行文; 実行文; ... ・行列のvectorを区切るcolon: vector: vector: ... ・vectorの要素||関数の引数を区切るcomma, 要素, 要素, ... 引数, 引数, ... 区切り文字は2項演算子のassociativityや階層の深さとは無関係に左から順に演算する ・区切り文字の演算のprecedenceは最優先 x=3,(x=9),2x -> (0,0,18) x -> 9 ・よって変数は実行直前ではなく列挙直前の代入値を参照する x=3; x=2:3x -> (0:6) 区切り文字はNativeのcomma演算子同様に働くが、行列の次元は残る (x=1,x=2x:x=2x,x) -> (0,0:0,4) {x=1,x=2x:x=2x,x} -> (0,0:0,4) |
|
目次
最上位関数 入力仕様 |
最上位関数の入力仕様と付随する留意事項について記述する
以下の最上位関数は括弧より優先する ・Ver.2.31.17以降、addVar/addEqn/hasV/hasE最上位関数を追加 ・Ver.2.243.56以降、hasVs/hasEs最上位関数を追加 ・Ver.2.268.62以降、var||eqnを統合 hasVs ⇒ hass(varName_in_self_scope) hasEs ⇒ hass(=<eqnName_in_self_scope) hasV ⇒ has(varName) hasE ⇒ has(=<eqnName) hasVar ⇒ has__(varName_in_storage) hasEqn ⇒ has__(=<eqnName_in_storage) delVar ⇒ del__(varName_in_storage) delEqn ⇒ del__(=<eqnName_in_storage) addVar ⇒ add__(varName_in_storage) addEqn ⇒ add__(=<eqnName_in_storage) ・double-underscore__の意味:仕様廃止の可能性あり clear; t0=(1,2,3:4,5,6); representation_scope2storage=<[xt=t0.,yt=(t0)i.,out_lazy=<{=<xt,=<yt},=<out_lazy]=>; representation_scope2storage=>xy; xt=(xy=>)[0]=>; yt=(xy=>)[1]=>; (xt,yt) -> (1,4,i,4i:2,5,2i,5i:3,6,3i,6i) clear; t0=(1,2,3:4,5,6); representation_scope2storage=<[xt=t0,yt=(t0)i,out_lazy=<{=<xt,=<yt},=<out_lazy]=>; representation_scope2storage=>xy; xt=(xy=>)[0]=>; yt=(xy=>)[1]=>; (xt:yt) -> (1,2,3:4,5,6:i,2i,3i:4i,5i,6i) hasVar最上位関数 ・変数のlocal storage存在可否を判定する ・引数 ・第1引数: 変数名symbol ・返値 ・exist時: 1を返す ・not exist時: 0を返す ・test caseを列挙する clear; a=2; hasVar(a) -> 1 clear; a=2; hasVar(b) -> 0 ・第1引数は最終要素を参照する clear; a=2; hasVar(b,c:a) -> 1 clear; a=2; hasVar(a,b:c) -> 0 clear; a=2; hasVar((b,a),c) -> 0 clear; a=2; hasVar({b,a},c) -> 1 ・引数不正の場合、error終了 hasVar() -> [MyErr]Invalid FNc(hasvar) hasVar(2) || hasVar(a=2) -> [MyErr]Invalid hasvar arguments hasEqn最上位関数 ・式変数のlocal storage存在可否を判定する ・hasVar最上位関数同様 ・test caseを列挙する clear; a=2; hasEqn(a) -> 0 clear; a=<2; hasEqn(a) -> 1 clear; a=<2; hasEqn(b) -> 0 delVar最上位関数 ・変数をlocal storageから削除する ・引数 ・第1引数: 変数名symbol ・返値 ・削除対象exist時: 1を返す ・削除対象not exist時: 0を返す ・test caseを列挙する clear; a=2; delVar(a) -> 1 clear; a=2; delVar(b) -> 0 clear; a=2; (delVar(a)) -> 1 clear; a=2; (delVar(a),a) // a deleted -> [MyErr]Invalid REv(a) clear; a=2; (delVar(b),a) -> (0,2) clear; a=2; a*delVar(a) // a deleted -> [MyErr]Invalid binary operation ・第1引数は最終要素を参照する clear; a=2; (delVar(b,c:a),a) // a deleted -> [MyErr]Invalid REv(a) clear; a=2; (delVar(a,b:c),a) -> (0,2) clear; a=2; (delVar((b,a),c),a) -> (0,2) clear; a=2; (delVar({b,a},c),a) // a deleted -> [MyErr]Invalid REv(a) delEqn最上位関数 ・式変数をlocal storageから削除する ・delVar最上位関数同様 ・test caseを列挙する clear; a=2; delEqn(a) -> 0 clear; a=<2; delEqn(a) -> 1 clear; a=<2; delEqn(b) -> 0 clear; a=<2; (delEqn(a)) -> 1 clear; a=<2; (delEqn(a),a=>) // a deleted -> [MyErr]Invalid REv(a) clear; a=<2; (delEqn(b),a=>) -> (0,2) ・命令文を使用 clear; a=<2; store; delEqn(a); a=> // a deleted -> [MyErr]Invalid REv(a) clear; a=<2; store; delEqn(a); restore; a=> -> 2 addVar最上位関数 ・scope変数の変数をlocal storageに追加する ・引数 ・第1引数: 変数名symbol ・返値 ・追加対象exist時: 1を返す ・追加対象not exist時: 0を返す ・test caseを列挙する clear; a=<2; addVar(a) -> 0 clear; a=2; addVar(a) -> 1 clear; a=2; addVar(a),addVar(a) -> (1,1) clear; a=2; addVar(a); a -> 2 clear; a=2; addVar(b) -> 0 clear; a=2; addVar(b); a -> 2 clear; [a=2,]; a -> [MyErr]Invalid REv(a) clear; [a=2,addVar(a)]; a -> 2 clear; [a=2,[a=3,addVar(a)]]; a -> 3 clear; [a=2,[a=3,[a=4,addVar(a)]]]; a -> 4 clear; [a=2,[a=3,[a=4,[a=5,],addVar(a)]]]; a -> 4 clear; [a=2,[a=3,[[a=5,],addVar(a)]]]; a -> [MyErr]Invalid REv(a) clear; [a=2,[a=3,([a=5,],addVar(a))]]; a -> 3 addEqn最上位関数 ・scope変数の式変数をlocal storageに追加する ・addVar最上位関数同様 ・test caseを列挙する clear; a=2; addEqn(a) -> 0 clear; a=<2; addEqn(a) -> 1 clear; a=<2; addEqn(a),addEqn(a) -> (1,1) clear; a=<2; addEqn(a); a=> -> 2 clear; a=<2; addEqn(b) -> 0 clear; a=<2; addEqn(b); a=> -> 2 clear; [a=<2,]; a=> -> [MyErr]Invalid REv(a) clear; [a=<2,addEqn(a)]; a=> -> 2 clear; [a=<2,[a=<3,addEqn(a)]]; a=> -> 3 clear; [a=<2,[a=<3,[a=<4,addEqn(a)]]]; a=> -> 4 clear; [a=<2,[a=<3,[a=<4,[a=<5,],addEqn(a)]]]; a=> -> 4 clear; [a=<2,[a=<3,[[a=<5,],addEqn(a)]]]; a=> -> [MyErr]Invalid REv(a) clear; [a=<2,[a=<3,([a=<5,],addEqn(a))]]; a=> -> 3 hasV最上位関数 ・変数の直列scope内存在可否を判定する ・引数 ・第1引数: 変数名symbol ・返値 ・exist時: 1を返す ・not exist時: 0を返す ・test caseを列挙する clear; a=<2; hasV(a) -> 0 clear; a=2; hasV(a) -> 1 clear; a=2; hasV(b) -> 0 clear; a=2; hasV(a),[b=3,hasV(a),hasV(b)],hasV(b) -> (1,0,1,1,0) clear; a=2; hasV(a),[b=3,[hasV(a),hasV(b)]],hasV(b) -> (1,0,1,1,0) hasVs最上位関数 ・変数のscope変数存在可否を判定する hasE最上位関数 ・式変数の直列scope内存在可否を判定する ・hasV最上位関数同様 ・test caseを列挙する clear; a=2; hasE(a) -> 0 clear; a=<2; hasE(a) -> 1 clear; a=<2; hasE(b) -> 0 clear; a=<2; hasE(a),[b=<3,hasE(a),hasE(b)],hasE(b) -> (1,0,1,1,0) clear; a=<2; hasE(a),[b=<3,[hasE(a),hasE(b)]],hasE(b) -> (1,0,1,1,0) hasEs最上位関数 ・式変数のscope変数存在可否を判定する 留意事項を列挙する ・add/del最上位関数は参照透過性の対策用でscope単位の操作不可(命令文参照) ・引数に演算子(上位を含む)の使用不可 hasVar(a||b) -> [MyErr]Invalid binary operation ・Ver.2.157.38以降、最上位関数より上位の論理演算子(短絡評価)を追加 hasVar(a|||b) -> [MyErr]Undef var||| clear; a=1; b=1; hasVar(a) && hasVar(b) -> 1 clear; a=1; b=1; hasVar(a) &&& hasVar(b) -> 1 ・Ver.2.196.46以降、論理値literalを返す ・Ver.2.268.62以降、error判定処理を削除 has__(a|||b) || has__(a) -> |
|
目次
括弧 入力仕様 |
括弧の入力仕様と付随する留意事項について記述する
実行文の一部を括る括弧は3種類使用可 優先順に列挙する ・波括弧{} ・丸括弧() ・角括弧[] 括弧は区切り文字に含める ・実行文を区切るsemi-colon;を括弧の中で使用した場合、error終了 (;) -> [MyErr]Invalid {([])} ・対応関係が取れない括弧のnestingが見つかった場合、error終了 [(0]) -> [MyErr]Invalid {([])} 丸括弧()は行vectorをcolon:区切りで列挙する ・角括弧[]は丸括弧()に準ずる (行vector: 行vector: ...) || [行vector: 行vector: ...] 波括弧{}は列vectorをcolon:区切りで列挙する {列vector: 列vector: ...} 無次元の演算の場合、要素を括る丸括弧()と波括弧{}は区別しない ・列挙しなければ括弧の種類は区別しない 有次元の場合、vectorを括る丸括弧()と波括弧{}は互いに転置の関係 (1,2:3,4) -> (1,2:3,4) {1,2:3,4} -> (1,3:2,4) ・転置行列関数を使用 transpose({1,2:3,4}) || trans({1,2:3,4}) -> (1,2:3,4) 関数の引数を括る括弧は丸括弧()で統一する(last行列関数を除く) ・波括弧{}を使用した場合、引数が転置される trans(1,2:3,4) -> (1,3:2,4) trans{1,2:3,4} -> (1,2:3,4) max(2,1) -> 2 max{2,1} -> (2:1) 括弧なしで要素を列挙した場合、行vector扱いの丸括弧()で括られる 1,2,3 -> (1,2,3) 演算結果のlog表示は丸括弧() {1,2:3,4} || [1,3:2,4] -> (1,3:2,4) |
|
目次
括弧の associativity 入力仕様 |
括弧のassociativityの入力仕様と付随する留意事項について記述する
vectorを括る丸括弧()と波括弧{}は互いに転置の関係で括弧のassociativityが存在する ・行列結合の逐次、括弧の種類を判別 1重列挙の場合、外側に括弧のassociativityは存在しない (1,2) || {(1,2)} || ({(1,2)}) || {({(1,2)})} -> (1,2) {1,2} || ({1,2}) || {({1,2})} || ({({1,2})}) -> (1:2) ・よって上流で列挙しない限り、変数・式変数は任意の括弧で括れる x=(1,2); y={1,2}; x*y || (x)(y) || {x}{y} || ({x}{y}) || {{x}{y}} -> 5 x=<(1,2); y=<{1,2}; x*y || (x)(y) || {x}{y} || ({x}{y}) || {{x}{y}} -> 5 2重列挙の場合 ・変数を使用 x=(1,2); y={3,4}; (x,y) -> (1,2,3:0,0,4) x=(1,2); y={3,4}; (x:y) -> (1,2:3:4) x=(1,2); y={3,4}; {x,y} -> (1,2:3:4) x=(1,2); y={3,4}; {x:y} -> (1,2,3:0,0,4) ・式変数も同様 x=<(1,2); y=<{3,4}; (x,y) -> (1,2,3:0,0,4) x=<(1,2); y=<{3,4}; (x:y) -> (1,2:3:4) x=<(1,2); y=<{3,4}; {x,y} -> (1,2:3:4) x=<(1,2); y=<{3,4}; {x:y} -> (1,2,3:0,0,4) x=<(1,2); y=<{3,4}; z=<(x,y); z -> (1,2,3:0,0,4) x=<(1,2); y=<{3,4}; z=<(x:y); z -> (1,2:3:4) x=<(1,2); y=<{3,4}; z=<{x,y}; z -> (1,2:3:4) x=<(1,2); y=<{3,4}; z=<{x:y}; z -> (1,2,3:0,0,4) ・欠損要素は0として演算する ・転置行列関数を使用 trans(trans((1,2:3:4))) -> (1,2:3,0:4,0) trans(trans{(1,2:3:4)}) -> (1,2:3,0:4,0) trans{trans{(1,2:3:4)}} -> (1,2:3,0:4,0) x=(1,2); y={3,4}; trans(trans((x:y))) -> (1,2:3,0:4,0) |
|
目次
角括弧 入力仕様 |
角括弧[]の入力仕様と付随する留意事項について記述する
角括弧[]は次の規則で直前の行列要素の行/列indexを指定する 行列[行index][列index] 変数[行index][列index] 式変数[行index][列index]=> || (式変数=>)[行index][列index] 式変数[行index][列index](arguments)=> || (式変数(arguments)=>)[行index][列index] 詳細は行列操作参照 仕様を列挙する ・括弧の中で最下位の演算のprecedence ・Right-Associativity(右から左を参照) ・Ver.2.158.38以降、行列結合用の空行列に流用 [] -> [] ・複数の要素を持つ場合、行列として代用可 A=(1,2:3,4); A[1,2:3,4] -> (7,10:15,22) [1,2][0][0] -> 1 [1,2:3,4][0] -> (1,2) [1,2:3,4][1] -> (3,4) ・Ver.2.170.41以降、列参照と列代入の[e]を空行列で代替可 Ver.2.747.112以降、列参照と列代入の[e]を廃止 [1,2:3,4][][1] -> (2:4) A=[1,2:3,4]; A[][1]={-2,-4}; A -> (1,-2:3,-4) Ver.2.31.17以降、変数のscopeを追加(上記仕様の冗長性を活用) ・複数の要素を持つcaseのみ、変数のscope有効 clear; 3*[a=2] || 3*[0] -> [MyErr]Invalid BRdm(*) clear; [a=2]*3 || [0]*3 -> [MyErr]Invalid reference clear; 3*[a=2,a] || 3*[0,2] -> (0,6) ・式変数のargumentsを括る場合、closure無効 clear; f(x)=<x; f(2)=>,x -> (2,2) clear; f[x]=<x; f(2)=>,x -> (2,2) clear; f[x,y]=<x; f(2,false)=>,x -> (2,2) clear; x=1; f[x]=<x; f(2)=>,x -> (2,1) ・単独scope clear; x=1; f[x]=<last[,x]; f(2)=>,x -> (2,1) ・Ver.2.88.32以降、定義できない乗算||減算||加算を拡張行列演算に追加 clear; [a=2,a]*3 || [0,2]*3 -> (0,6) clear; 3*[a=2,a]; a -> [MyErr]Invalid REv(a) 詳細は変数のscope参照 |
|
目次
空括弧 入力仕様 |
空括弧の入力仕様と付随する留意事項について記述する
以下の空括弧はparse段階で除去する () -> {} -> ・Ver.2.158.38以降、空行列を除く [] -> [] ・Ver.2.272.63以降、空括弧の判別を厳格化 無条件に削除 ⇒ 定数()のみ削除・波括弧{}禁止 test caseを列挙する ()3()3() || 3*3 -> 9 ()3()/()3() || 3/3 -> 1 (()) -> 0 ((())) -> 0 {{}} -> 0 {{{}}} -> 0 ・定数 pi() -> 3.141592653589793 e() -> 2.718281828459045 |
|
目次
予約語 入力仕様 |
予約語の入力仕様と付随する留意事項について記述する
予約語の種類を列挙する ・Graphing Calculator's plot2d-command ・white spaces ・comment文 ・命令文 ・区切り文字・括弧 ・定数含む関数名 ・演算子記号 ・reserved token記号\||?||#||.||'||"||` Ver.2.165.39以降、追加 ・escape記号 Ver.2.301.72以降、追加 ・operand記号 ・NaN||論理値literal Ver.2.158.38以降、追加 ・予約変数 ・実数値の10進数literal小数点. ・実数値の10進数literal指数e||E ・実数値の16進数literal接頭辞0x||0X ・実数値の2進数literal接頭辞0b||0B Ver.2.146.37以降、ECMAScript6対応環境の場合 ・実数値の8進数literal接頭辞0o||0O Ver.2.146.37以降、ECMAScript6対応環境の場合 予約語の規則を列挙する ・大文字・小文字・全角・半角を区別しない ・変数名・式変数名に使用不可(変数の命名規則参照) stop=3 -> [MyErr]Invalid stop called max=3 -> [MyErr]Invalid ans isFound max=<3 -> [MyErr]Invalid BTe([object Object]) MAX=3 -> [MyErr]Invalid ans isFound ・Ver.2.221.50以降、実装関数名の大文字・小文字のformatを選択するuseFuncを追加 予約語の一覧は内部仕様参照 |
|
目次
実数値 入力仕様 |
実数値の入力仕様と付随する留意事項について記述する
実数値の定義:built-inのNumber関数が数値と認識する文字列 非数NaNの定義:built-inのNumber関数が数値と認識しない文字列 test caseを列挙する 123 -> 123 -123 -> -123 ・0開始の場合、10進数literal(古いbrowserでは8進数literalの可能性あり) 0123 -> 123 00123 -> 123 -0123 -> -123 -00123 -> -123 ・10進数literal小数(小数表記) 0.123 -> 0.123 -0.123 -> -0.123 .123 -> 0.123 -.123 -> -0.123 123. -> 123 -123. -> -123 ・10進数literal指数(指数表記) 0123e0 -> 123 0123e+1 -> 1230 -0123e-2 -> -1.23 0.123e+1 -> 1.23 -0.123e-2 -> -0.00123 -0123.4e+5 -> -12340000 ・16進数literal(符号なし) 0x0 -> 0 0x000 -> 0 0xf -> 15 0xfff -> 4095 0x0b -> 11 ・非数NaN(演算を伴うため、実数値以外の判定) +0x00 || +(0x00) -> 0 -0x00 || -(0x00) -> 0 -0xff || -(0xff) -> -255 0x0e+1 || (0x0e)+1 -> 15 0x1e-2 || (0x1e)-2 -> 28 -0x1e2 || -(0x1e2) -> -482 0x0.0 -> [MyErr]Invalid ans isFound 00x0 -> [MyErr]Invalid ans isFound ・Ver.2.146.37以降、接頭辞判定の正規表現を修正 0x3i -> [MyErr]Invalid varName(0x3i) 0x0o -> [MyErr]Invalid varName(0x0o) ・Ver.2.146.37以降、2進数literal(符号なし) 0b011 -> 3 0b02 -> [MyErr]Invalid varName(0b02) 0b0f -> [MyErr]Invalid varName(0b0f) ・Ver.2.146.37以降、8進数literal(符号なし) 0o17 -> 15 0b08 -> [MyErr]Invalid varName(0b08) 0b0f -> [MyErr]Invalid varName(0b0f) built-inのNumber関数の挙動を確認する場合、Number変換参照 |
|
目次
false判定値 入力仕様 |
false判定値の入力仕様と付随する留意事項について記述する
false判定値の定義:無次元の0||false||NaN(数値誤差は無視) ・Ver.2.158.38以降、NaNを追加 ・Ver.2.159.38以降、虚部のisNaN判定を統一:isNaN(実部&&虚部) ⇒ isNaN(実部)||isNaN(虚部) ・Ver.2.165.40以降、falseを追加 無次元のtrue判定値の定義 ・実数演算:false判定値以外の実数値 ・複素数演算:false判定値以外の複素数 有次元のtrue判定の定義:要素数が2以上(値は無視) 有次元のtrue判定を使用する項目を列挙する ・論理演算子(短絡評価) ・Ver.2.196.46以降、論理演算子(literal) test caseを列挙する val=0; val==0,val==false,val===0,val===false -> (1,1,1,0+O(1e+0)) val=false; val==0,val==false,val===0,val===false -> (1,1,0+O(1e+0),1) val=1; val==1,val==true,val===1,val===true -> (1,1,1,0+O(1e+0)) val=true; val==1,val==true,val===1,val===true -> (1,1,0+O(1e+0),1) ・Ver.2.172.42以降、isFalse/isTrue行列関数を追加 |
|
目次
欠損値 入力仕様 |
欠損値の入力仕様と付随する留意事項について記述する
各機能の欠損値の定義を列挙する ・csv-readの欠損値=NaN ・plot2d-commandの欠損値=NaN+(NaN)i ・method演算子の欠損値=NaN+(NaN)i ・補間関数の欠損値=NaN+(NaN)i ・reshape行列関数の欠損値=NaN+(NaN)i ・座標形式行列関数の欠損値=.filter演算子の欠損値=NaN+(NaN)i ・Ver.2.819.132以降、区間[∞,∞]の極限が有限でない場合、積分の欠損値=NaN+(NaN)i |
|
目次
定数 入力仕様 |
定数の入力仕様と付随する留意事項について記述する
Number型を含む定数は引数括弧なしで厳密には関数に含めない ・実行文を作るparse段階で数値に変換する ・Excel準拠で空括弧()付を許容する ・空括弧()はparse段階で除去する(Ver.2.158.38以降、空行列を除く) 関数を使用して円周率piとNapier数eを一例に示す PI() || pi || 2acos(0) || 2asin(1) || 4atan(1) -> 3.141592653589793 E() || e || e^1 || exp(1) -> 2.718281828459045 eは指数表記と区別するため、空括弧()を付ける方が間違いが少ない 2e-1 || 2E-1 -> 0.2 2e()-1 || 2E()-1 -> 4.43656365691809 ・記号省略乗算を許容した弊害への対策 Ver.2.30.15以降、乱数は引数0個の関数に昇格 ・本来、関数call時に空括弧を含めて判別するが、 ・定数の引数括弧の有無と記号省略乗算を同時に許容した弊害への対策 次の場合、代入errorとは判別されず、右辺に移項して演算される pi=3 || pi()=3 || =3-pi -> -0.14159265358979312 ・parse後の実行文を示す 3.141592653589793=3 || =3-3.141592653589793 -> -0.14159265358979312 詳細は特殊仕様参照 |
|
目次
記号省略乗算 入力仕様 |
記号省略乗算入力仕様と付随する留意事項について記述する
2πの演算方法を円周率piを使用して次に示す 2pi || 2*pi -> 6.283185307179586 ・pi2と入力した場合、変数と判別される pi2 -> [MyErr]Invalid REv(pi2) ・piの後に続ける場合、括弧で区切るか乗算記号*を明示する pi(2) || pi*2 -> 6.283185307179586 角括弧[]は使用不可 pi[2] -> [MyErr]Invalid reference of array [2]pi -> [MyErr]Invalid reference x=2; x[0] -> 2 x=2; x[2] -> [MyErr]Invalid reference of array x=2; [2]x -> [MyErr]Invalid reference Ver.2.32.17以降、式変数のargumentsを追加 ・記号省略乗算よりcall先argumentsを優先する(Ver.2.43.22追記) clear; x(t)=<-t; f=<x(1)+1; f -> 0 clear; x(t)=<-t; f=<x(1)2+1; f -> -1 clear; x(t)=<-t; f=<x(1)(2)+1; f -> -1 clear; x(t)=<-t; f=<(x(1))(2)+1; f -> -1 clear; x(t)=<-t; f=<x(1(-2))+1; f -> 3 clear; x(t)=<-t; f=<x(1(-2))(2)+1; f -> 5 clear; x(t)=<-t; f=<x(1(-2))2+1; f -> 5 clear; x(t)=<-t; f=<x((1(-2))3)+1; f -> 7 clear; x(t)=<-t; f=<x((1(-2))3+1); f -> 5 clear; x(t)=<-t; x=-999; f=<x(1)+1; f -> -998 clear; x(t)=<-t; x=-999; f=<x(1)=>+1; f -> 0 clear; x(t)=<-t; x=-999; f=<x(1)=>2+1; f -> -1 clear; x(t)=<-t; x=-999; f=<x(1)=>(x)+1; f -> 1000 clear; x(t)=<-t; x=-999; f=<x(1)=>x+1; f -> 0 clear; x(t)=<-t; x=-999; f=<x(1)=>x+1; f; x -> -1 |
|
目次
複素数 入力仕様 |
複素数の入力仕様と付随する留意事項について記述する
虚数単位iは後置単項演算子とする (+1)i || +(1)i || +1(i) || +(i) -> i (-1)i || -(1)i || -1(i) || -(i) -> -i (i)i || i(i) || i*i -> -1 3i/2 -> 1.5i 1/2i || 1/(2i) -> -0.5i ・Ver.2.158.38以降、literalを追加 0i || (0)i || (false)i || 0*i -> 0 1i || (1)i || (true)i || 1*i -> i (NaN)i || NaN*i -> NaN 複素数を宣言する関数を示す complex(1,-1) || comp(1,-1) -> 1-i 複素数を実部と虚部に分離する関数を示す real(3+i) -> 3 imag(3+i) -> 1 iの2乗の演算結果を示す i*i || (-i)*(-i) -> -1 ・中置2項演算子||pow関数を使用 (i)^2 || (i)**2 || pow(i,2) -> -1+1.2246467991473532e-16i ・浮動小数点演算では、次のMachine epsilonが残る epsilon || eps -> 2.220446049250313e-16 ・この傾向は演算量に応じて実数演算より顕著に現れる -1の正の平方根の演算結果を示す ・中置2項演算子||sqrt関数||pow関数を使用 (-1)^0.5 || sqrt(-1) || pow(-1,0.5) -> 6.123233995736766e-17+i ・先頭の丸括弧()を省略した場合、次のように演算される -1^0.5 || -(1^0.5) -> -1 ・符号付の分母の丸括弧()を省略した場合、error終了 1/-i || (1/)(-i) -> [MyErr]Invalid binary operation 1/(-i) -> i Napier数eの空括弧()を省略してEulerの公式から極形式の複素数を示す (sqrt2)e^(i{pi/4}) || sqrt2()ecomp(pi/4) -> 1.0000000000000002+i sqrt2 || sqrt2() -> 1.4142135623730951 変数を使用 ・複素数zの偏角/piを示す z=e^(i{pi/4}); arg(z)/pi -> 0.25 ・複素数zの絶対値を示す z=e^(i{pi/4}); abs(z) -> 1 以上より、次の複素数演算をtest caseとして初期表示する e^(-i(1pi()2/2i(5-3-1)i/(-4))) ・2項演算子のassociativityはLA既定で除算より記号省略乗算を優先する e^(-i(1pi(){2/{2i({5-3}-1)i}}/(-4))) 2項演算子のassociativityや演算子のprecedenceによって解が異なる場合、入力を見直す 具体的には次のように対策する a={5-3}-1; b=2/{2i(a)i}; e^(-i(1pi()b/(-4))) ・一部分を変数に代入し、semi-colon;区切りで演算順序を明確化する ・中置2項演算子が連続する場合、括弧を明示する 実数演算の場合、虚数は0のため、次の極形式は使用不可 t=pi/4; e^(i{t}) || e^(real(i)t) || e^(0) // NG -> 1 ・極形式の関数を使用 pcomp(1,t) || ecomp(t) || cos(t)+real(i)sin(t) || cos(t) -> 0.7071067811865476 |
|
目次
関数 入力仕様 |
関数の入力仕様と付随する留意事項について記述する
関数の引数を括る括弧は丸括弧()で統一する(last行列関数を除く) 関数の引数に行列を指定した場合、 Ver.2.73.29以降、各行vectorの左から順に参照する ・引数1個の関数の場合 clear; x=(1,2,3); log(x) || log(1) -> 0 clear; x=(1,2,3:4,5,6); log(x) || (log(1):log(4)) -> (0:1.3862943611198906) ・引数1個||2個の関数の場合 clear; x=(1,2,3); log_ex(x) || log_ex(1,2) -> 0 clear; x=(1,2,3:4); log_ex(x) || (log_ex(1,2):log_ex(4)) -> (0:0.6020599913279623) ・引数2個の関数の場合 clear; x=(1,2,3); atan2(x) || atan2(1,2) -> 0.4636476090008061 clear; x=(1,2,3:4,5,6); atan2(x) || (atan2(1,2):atan2(4,5)) -> (0.4636476090008061:0.6747409422235527) clear; x=(1,2,3:4); atan2(x) || (atan2(1,2):atan2(4)) -> (0.4636476090008061:NaN) ・引数不定の関数の場合 clear; x=(1,2,3); max(x) || max(1,2,3) -> 3 clear; x=(1,2,3:4,5,6); max(x) || (max(1,2,3):max(4,5,6)) -> (3:6) clear; x=(1,2,3:4,5,6); lcm(x) || (lcm(1,2,3):lcm(4,5,6)) -> (6:60) clear; x=(1,2,3:4*(1,2,3)); gcd(x) || (gcd(1,2,3):gcd(4*(1,2,3))) -> (1:4) |
|
目次
関数の引数 入力仕様 |
関数の引数の入力仕様と付随する留意事項について記述する
Ver.2.170.42以降、実装関数の引数がNaNの場合、発生する不具合を一括修正 pow(NaN,2) -> NaN pow(2,NaN) -> NaN ・引数不足の場合、NaNを返す pow(2) -> NaN ・引数不定の関数の場合、同じ引数を追加して正常化 camin(NaN) || camin(NaN,NaN) -> NaN camin(i) || camin(i,i) -> 1 詳細はNaN対応参照 |
|
目次
isNaN関数 入力仕様 |
isNaN関数の入力仕様と付随する留意事項について記述する
Ver.2.159.38以降、isNaN関数を追加 test caseを列挙する isNaN(NaN) -> true isNaN(Infinity) -> false isNaN(0) -> false isNaN(false) -> false isNaN(true) -> false val=NaN; isNaN(val) -> true mat=(NaN,2:3,NaN); isNaN(mat) || isNaN(NaN:3) -> (true:false) a=0; b=a/a; c=1/a; isNaN(a),isNaN(b),isNaN(c) -> (false,true,true) ・実数演算 a=0; b=a/a; c=1/a; isNaN(a),isNaN(b),isNaN(c) -> (false,true,false+O(1e+0)) ・Ver.2.163.39以降、虚部のNaNをlog表示する場合、内部option参照 nan*i -> NaN+(NaN)i ・Ver.2.167.41以降、実部NaN+虚部iの演算結果のlog表示不具合を修正 NaN+i -> NaN 留意事項を列挙する ・論理値literalを返す |
|
目次
演算子 代替関数 入力仕様 |
演算子代替関数の入力仕様と付随する留意事項について記述する
演算子代替関数の仕様を列挙する ・ ・数値誤差は無視 ・Ver.2.170.42以降、引数不足の場合、NaNを返す pow(2) -> NaN or(NaN) || or(0) -> NaN 表記上の留意事項を列挙する ・追加実装の演算子 ・2項演算子のassociativityに依存する演算子と代替関数 複素数演算の演算子代替関数(operandが無次元の複素数) ・left**right代替のべき乗関数: pow(left, right) || power(left, right) ・Ver.2.168.41以降、strict equal判定関数: cseq(left, right) ・Ver.2.168.41以降、strict not equal判定関数: csne(left, right) ・equal判定関数: ceq(left, right) ・not equal判定関数: cne(left, right) ・Ver.2.168.41以降、以下の代替関数を追加 ・~~(right): cnot(right) ・left&&right: cand(left, right) ・cnot(cand(left, right)): cnand(left, right) Ver.2.766.116以降、追加 ・left@@right: cxor(left, right) ・cnot(cxor(left, right)): cxnor(left, right) Ver.2.766.116以降、追加 ・left||right: cor(left, right) ・cnot(cor(left, right)): cnor(left, right) Ver.2.766.116以降、追加 実数演算の演算子代替関数(operandが無次元の実数値) ・left%right代替の剰余関数: mod(left, right) ・left%%right代替の整数商関数: quot(left, right) fmod対応のfquot関数: fquot(left, right) Ver.2.721.101以降、追加 ・Ver.2.167.40以降、left===rightを代替するstrict equal判定関数: seq(left, right) ・Ver.2.167.40以降、left!==rightを代替するstrict not equal判定関数: sne(left, right) ・left==rightを代替するequal判定関数: eq(left, right) ・left<>rightを代替するnot equal判定関数: ne(left, right) ・left<rightを代替するless than判定関数: lt(left, right) ・left<=rightを代替するless or equal判定関数: le(left, right) ・left>rightを代替するgreater than判定関数: gt(left, right) ・left>=rightを代替するgreater or equal判定関数: ge(left, right) ・Ver.2.167.40以降、以下の代替関数を追加 ・~right: bitnot(right) ・left&right: bitand(left, right) ・left^rightを表すleft@right: bitxor(left, right) ・left|right: bitor(left, right) ・(right?0:1)を表す~~(right): not(right) ・left&&right: and(left, right) ・not(and(left, right)): nand(left, right) Ver.2.766.116以降、追加 ・(left?1:0)^(right?1:0)を表すleft@@right: xor(left, right) ・not(xor(left, right)) || Kdelta(left, right): xnor(left, right) Ver.2.766.116以降、追加 ・left||right: or(left, right) ・not(or(left, right)): nor(left, right) Ver.2.766.116以降、追加 test caseを列挙する i**i,i^i -> (0.20787957635076193,0.20787957635076193) pow(i,i),power(i,i) -> (0.20787957635076193,0.20787957635076193) 5.2%3 -> 2.2 ・Ver.2.721.101以降、fmod関数は常に正の余りを返す mod(5.2,3),fmod(5.2+i,3),fmod(5.2,3+i) -> (2.2,2.2,2.2) 1%5,mod(1,5),fmod(1,5) -> (1,1,1) -1%5,mod(-1,5),fmod(-1,5) -> (-1,-1, 1%(-5),mod(1,-5),fmod(1,-5) -> (1,1,1) -1%(-5),mod(-1,-5),fmod(-1,-5) -> (-1,-1, -7%5,mod(-7,5),fmod(-7,5) -> (-2,-2, ・Ver.2.721.101以降、fquot関数を追加 quot(5.2,3),quot(5.2,2),fquot(5.2,3),fquot(5.2,2) -> (1,2,1,2) 1%%5,quot(1,5),fquot(1,5) -> (0,0,0) -1%%5,quot(-1,5),fquot(-1,5) -> (0,0,-1) 1%%(-5),quot(1,-5),fquot(1,-5) -> (0,0,0) -1%%(-5),quot(-1,-5),fquot(-1,-5) -> (0,0,1) -7%%5,quot(-7,5),fquot(-7,5) -> (-1,-1,-2) ceq(2+3i,3*i-(-2)) -> 1 cne(2+3i,3*i-(-2)) -> 0 eq(2+3i,2-3i) || eq(2,2) -> 1 ne(5,-5) -> 1 lt(1,2)<(3,4) || 1&1 // AND -> 1 lt(1,2)>(3,4) || 1&0 // AND -> 0 lt(1,2)@lt(3,4) || 1@1 // XOR -> 0 lt(1,2)@gt(3,4) || 1@0 // XOR -> 1 lt(1,2)|lt(3,4) || 1|1 // OR -> 1 lt(1,2)|gt(3,4) || 1|0 // OR -> 1 le(1,1)*ge(1,1) || 1*1 -> 1 le(1,1)*ge(1,2) || 1*0 -> 0 ・拡張行列演算 left={5.2,5.2,5.2+i,5.2+i}; right={3,3+i,2,2+i,1,1+i}; left%right,mod(left,right),quot(left,right) -> ( 2.2,2.2,1: 2.2,2.2,1: 1.2000000000000002,1.2000000000000002,2: 1.2000000000000002,1.2000000000000002,2: 0.20000000000000018,NaN,NaN: 0.20000000000000018,NaN,NaN ) right=(false:true:NaN:0:1:i); cnot(right),not(right) -> ( 1,1: 0,0: 1,1: 1,1: 0,0: 0,1 ) 留意事項を列挙する 関数call前に引数のleftとrightを交換する特殊な条件分岐が増えるため、対応見送り ・Ver.2.193.44以降、mix-in切替で2項演算子のassociativityに依存する代替関数に対応 ・Ver.2.196.46以降、論理値literalを返す |
|
目次
int関数 入力仕様 |
int関数の入力仕様と付随する留意事項について記述する
int関数 ・Ver.2.87.32以降、0側に丸める int(3.2) -> 3 int(-3.2) -> -3 int(-4) -> -4 int(-3.2i) -> 0 floor関数 floor(3.2) -> 3 floor(-3.2) -> -4 floor(-4) -> -4 floor(-3.2i) -> 0 剰余・整数商演算子||演算子代替関数との関係 clear; a=-3.2; b=2; m=a-int(a/b)*b; m || mod(a,b) || -3.2%2 -> -1.2000000000000002 clear; a=-3.2; b=2; q=int(a/b); q || quot(a,b) || -3.2%%2 -> -1 clear; a=-3.2; b=2; m=a-floor(a/b)*b; m // NG -> 0.7999999999999998 clear; a=-3.2; b=2; q=floor(a/b); q // NG -> -2 留意事項を列挙する ・operandは実数のみ対応 |
|
目次
乱数関数 入力仕様 |
乱数関数の入力仕様と付随する留意事項について記述する
Ver.2.30.15以降、乱数の即時callに対応 ・Ver.2.272.63以降、引数0個の関数callを厳格化 丸括弧()の省略可 ⇒ 省略不可 乱数の仕様はbuilt-inのMath.random()に同義 ・返値は区間[0,1)の一様乱数(0以上~1未満の擬似乱数) ・乱数生成器のseed値は現在時刻(指定不可) test caseを列挙する random() || random || rand -> 0.7479324154774045 rand,rand -> (0.31204941180294865,0.4245907180242292) A=0; _rn(=<A=(A,rand),,2); A -> (0,0.12740820474199377,0.7111903938956377) ・Ver.2.158.38以降、行列結合用の空行列を追加 A=[]; _rn(=<A=(A,rand),,2); A -> (0.3371037693804637,0.6437029689436904) |
|
目次
その他の乱数 入力仕様 |
確率分布に従う乱数の入力仕様と付随する留意事項について記述する
確率密度関数の確率分布に従う乱数の生成方法 ・乱数の返値xを定義 ・確率密度関数の累積分布関数y=P(x) 確率分布が一様の場合、yは線形 確率分布が非一様の場合、yは非線形 ・累積分布関数の許容誤差範囲内で ・xの区間=[x0,x1)を定義 ・yの区間=[P(x0),P(x1))を満たす ・一様乱数生成器rand=[0,1)の関数y=y(rand)を定義 ・以上より、y=P(x)の逆変換x=Pinv(y(rand))を返す ・標準正規分布の許容誤差=5σの一例 xの区間=[-5,5) yの区間=(rand-0.5)*2*0.999999426697 SND(t)=<exp(-t^2/2)/sqrt(2*pi); P(x,N)=<_i((t)=<SND(t)=>,0,x,N)*2; P(5,10000) -> 0.9999994266968594+O(1e-13) ・逆変換x=Pinv(y)の方法 厳密には逆変換の解析関数を使用 簡単には逆変換のlookup-tableを使用 乱数生成の一例を示す ・標準正規分布の非常に粗い逆変換table:x=Pinv(y) csv0=( -0.999999427,-0.999936657,-0.997300203,-0.954499736,-0.682689492,0, 0.682689492,0.954499736,0.997300203,0.999936657,0.999999427: -5,-4,-3,-2,-1,0,1,2,3,4,5 ); ・統計関数を使用して昇順sort table=sort0(csv0); ・yの範囲を取得 ymin=min(table)[0]; ymax=max(table)[0]; ・一様乱数を生成してyに変換 y=ymin+(ymax-ymin)*rand; ・線形補間を使用してxに逆変換(その他の補間関数は次数が不適切で近似困難) x=interp(y:table); x -> 0.2128604699061138 |
|
目次
階乗関数 入力仕様 |
階乗関数の入力仕様と付随する留意事項について記述する
Ver.2.69.28以降、階乗の仕様を見直して次の致命的な不具合に繋がる入力を回避 Maximum call stack size exceeded ・再帰処理を単なるfor-loopに修正 ・順列||組合せ関数の引数不足による無限loopを修正 階乗の仕様を列挙する ・operandは0を含む自然数のみ対応 ・operandが負の場合、 ・operand=0の場合、1を返す ・Ver.2.205.46以降、引数の丸め方をfloor ⇒ roundに演算仕様変更 階乗fact(n) fact(3.3) || 3.3! || 3! || 3*2*1 -> 6 fact(3i) || (3i)! || 0! -> 1 fact(3+3i) || (3+3i)! || 3! || 3*2*1 -> 6 fact(-3) || (-3)! -> fact(0) || 0! -> 1 fact(1) || 1! || 1 -> 1 fact(2) || 2! || 2*1 -> 2 fact(3) || 3! || 3*2*1 -> 6 fact(4) || 4! || 4*3*2*1 -> 24 fact(5) || 5! || 5*4*3*2*1 -> 120 fact(6) || 6! || 6*5*4*3*2*1 -> 720 fact(7) || 7! || 7*6*5*4*3*2*1 -> 5040 fact(8) || 8! || 8*7*6*5*4*3*2*1 -> 40320 fact(9) || 9! || 9*8*7*6*5*4*3*2*1 -> 362880 fact(10) || 10! || 10*9*8*7*6*5*4*3*2*1 -> 3628800 fact(1e2) || 1e2! -> 9.332621544394418e+157 fact(1e3) || 1e3! -> Infinity fact(1e4) || 1e4! -> Infinity fact(1e5) || 1e5! -> Infinity fact(1e6) || 1e6! -> Infinity ・Ver.2.170.42以降、NaNの引数に対応 NaN! || fact(NaN) -> NaN 順列permutation(n,k) permut(3.3,1.6) || permut(3,1) || permutation(3,1) -> 3 permut(3i,1) || permut(0,1) -> 0 permut(3+3i,1) || permut(3,1) -> 3 permut(0,3) -> 0 permut(-1,3) -> permut(-1,0) -> permut(0,-1) -> permut(3,-1) -> permut(0,0) -> 1 permut(3,0) || 1 -> 1 permut(3,1) || 3 -> 3 permut(3,2) || 3*2 -> 6 permut(3,3) || 3*2*1 -> 6 permut(5,5) || 5*4*3*2*1 -> 120 permut(5,4) || 5*4*3*2 -> 120 permut(5,3) || 5*4*3 -> 60 permut(5,2) || 5*4 -> 20 permut(5,1) || 5 -> 5 permut(5,0) || 1 -> 1 permut(5,-1) -> ・Ver.2.170.42以降、引数不足の場合、NaNを返す permut(5) -> permut(1e2,1e2) || 1e2! -> 9.332621544394418e+157 permut(1e3,1e3) || 1e3! -> Infinity permut(1e4,1e4) || 1e4! -> Infinity permut(1e5,1e5) || 1e5! -> Infinity permut(1e6,1e6) || 1e6! -> Infinity ・Ver.2.170.42以降、NaNの引数に対応 permut(NaN,1) -> NaN 組合せcombination(n,r) ・Ver.2.205.46以降、引数の丸め方をfloor ⇒ roundに演算仕様変更 combin(3.3,1.6) || combin(3,2) || combination(3,2) -> 3 combin(3i,1) || combin(0,1) -> 0 combin(3+3i,1) || combin(3,1) -> 3 combin(0,3) -> 0 combin(-1,3) -> combin(-1,0) -> combin(0,-1) -> combin(3,-1) -> combin(0,0) -> 1 combin(3,0) || permut(3,0)/fact(0) || (1)/(1) -> 1 combin(3,1) || permut(3,1)/fact(1) || (3)/(1) -> 3 combin(3,2) || permut(3,2)/fact(2) || (3*2)/(2*1) -> 3 combin(3,3) || permut(3,3)/fact(3) || (3*2*1)/(3*2*1) -> 1 combin(5,5) || permut(5,5)/fact(5) || (5*4*3*2*1)/(5*4*3*2*1) -> 1 combin(5,4) || permut(5,4)/fact(4) || (5*4*3*2)/(4*3*2*1) -> 5 combin(5,3) || permut(5,3)/fact(3) || (5*4*3)/(3*2*1) -> 10 combin(5,2) || permut(5,2)/fact(2) || (5*4)/(2*1) -> 10 combin(5,1) || permut(5,1)/fact(1) || (5)/(1) -> 5 combin(5,0) || permut(5,0)/fact(0) || (1)/(1) -> 1 combin(5,-1) -> permut(5,-1)/fact(-1) || (0)/(0) -> NaN ・Ver.2.170.42以降、引数不足の場合、NaNを返す combin(5) -> combin(1e2,1e2) -> 1 ・複素数演算の場合 permut(1e2,1e2)/fact(1e2) // NG -> NaN 9.332621544394418e+157/9.332621544394418e+157 // NG -> NaN ・実数演算の場合 permut(1e2,1e2)/fact(1e2) // OK -> 1 9.332621544394418e+157/9.332621544394418e+157 // OK -> 1 combin(1e3,1e3) || Infinity/Infinity -> NaN combin(1e4,1e4) || Infinity/Infinity -> NaN combin(1e5,1e5) || Infinity/Infinity -> NaN combin(1e6,1e6) || Infinity/Infinity -> NaN ・Ver.2.170.42以降、NaNの引数に対応 combin(NaN,1) -> NaN |
|
目次
gcd/lcm関数 入力仕様 |
gcd/lcm関数の入力仕様と付随する留意事項について記述する
Ver.2.170.42以降、NaNの引数に対応 gcd(1,NaN) -> NaN 最大公約数を求めるgcd関数(Euclidの互除法) ・引数は正の整数のみ有効 a=111*12345; b=111*6789; c=111*111213; gcd(a,b,c) -> 333 ・結合的演算 gcd(gcd(a,b),c) || gcd(a,gcd(b,c)) -> 333 ・同義 gcd_(a0,b0)=<last[a=a0,b=b0,_rn(=<last{ia=int(a),ib=int(b),a=ib,b=ia%ib},,1e6,=<{b==0}),a]; gcd_(gcd_(a,b),c) || gcd_(a,gcd_(b,c)) -> 333 ・Ver.2.170.42以降、厳密な記述 ・Ver.2.205.46以降、整数の丸め方をfloor ⇒ roundに演算仕様変更 gcd_(a0,b0)=<last[ a=a0,b=b0,_rn(=<last{ia=round(a),ib=round(b),a=ia<0||ib===0&&&ia|||ib,b=ia%(ib||1)}, isBreak_a=<isNaN(a)|||a<0&&&~~(a=false),1e6,=<{isBreak_a|||b==0}),a]; ・0を含む場合 gcd(,) -> 0 gcd(0,2) -> 2 gcd(2,0) -> 2 gcd_(,) -> 0 gcd_(0,2) -> 2 gcd_(2,0) -> 2 ・引数不正の場合 gcd(1) -> 1 gcd(-1) -> false gcd(-1,2,-3) -> false gcd(-1,2) -> false gcd(-0.1,2) -> false gcd(1,-0.2) -> false gcd_(-1) -> [MyErr]Invalid args.length=2(gcd_) gcd_(-1,2) -> false gcd_(-0.1,2) -> false gcd_(1,-0.2) -> false ・Ver.2.170.42以降、NaNの引数に対応 gcd(NaN) || gcd(NaN,1) || gcd(1,NaN) -> NaN gcd_(NaN,1) || gcd_(1,NaN) -> NaN 最小公倍数を求めるlcm関数(gcdを使用) ・引数は0を含む自然数のみ有効 ・Ver.2.187.44以降、仮数部の桁数確保のため、括弧を明示 a=111*12345; b=111*6789; c=111*111213; lcm(a,b,c) -> 114956340053535 ・同義 ab=a*(b/gcd(a,b)); ab*(c/gcd(ab,c)) -> 114956340053535 ・0を含む場合 lcm(0,2) -> 0 lcm(2,0) -> 0 ・引数不正の場合 lcm(1) -> 1 lcm(-1) -> false lcm(-1,2,-3) -> false ・Ver.2.170.42以降、NaNの引数に対応 lcm(NaN) || lcm(NaN,1) || lcm(1,NaN) -> NaN |
|
目次
min/max関数 入力仕様 |
min/max関数の入力仕様と付随する留意事項について記述する
実数値の最小値を返すmin関数 x=(1,-2,3,-4,5,-6); min(x) -> -6 min(x:x*2) -> (-6:-12) ・複素数を含む場合、虚部=0 z=(-i,-2,3,-4,5+i,-6); min(z) -> -6 実数値の最大値を返すmax関数 x=(1,-2,3,-4,5,-6); max(x) -> 5 max(x:x*2) -> (5:10) ・複素数を含む場合、虚部=0 z=(-i,-2,3,-4,5+i,-6); max(z) -> 5 Ver.2.186.44以降、cmin/cmax関数の仕様変更 複素数絶対値が最小の要素を返すcmin関数 z=(-i,-2,3,-4,5+i,-6); cmin(z) -> -i cmin(z:z*(1+i)) -> (-i:1-i) cmin(NaN,1) -> NaN 複素数絶対値が最大の要素を返すcmax関数 z=(-i,-2,3,-4,5+i,-6); cmax(z) -> -6 cmax(z:z*(1+i)) -> (-6:-6-6i) cmax(1,NaN) -> NaN 偏角不問の場合、統計関数で代替可 z=(-6,6,-6i,6i,1,-2,3,-4,5); z_sorted=csort(z); z_sorted -> (1,-2,3,-4,5,-6,6,-6i,6i) z_reversed=creverse(z); z_reversed -> (6i,-6i,6,-6,5,-4,3,-2,1) first(z_sorted) -> 1 last(z_sorted) -> 6i first(z_reversed) -> 6i last(z_reversed) -> 1 |
|
目次
camin /camax関数 入力仕様 |
camin/camax関数の入力仕様と付随する留意事項について記述する
Ver.2.186.44以降、cmin/cmax関数 ⇒ camin/camax関数に関数名を変更 複素数絶対値の最小値を返すcamin関数 z=(1,-2,3,-4,5,-6)i; camin(z) -> 1 camin(z:z*(1+i)) -> (1:1.4142135623730951) ・同義 min(trans(abs(trans(z)))) -> 1 min(trans(abs(trans(z)),abs(trans(z*(1+i))))) -> (1:1.4142135623730951) ・Ver.2.170.42以降、引数1個の場合、同じ引数を2個目に追加して正常化 camin(i) || camin(i,i) -> 1 ・Ver.2.170.42以降、NaNの引数に対応 camin(NaN) || camin(NaN,NaN) -> NaN 複素数絶対値の最大値を返すcamax関数 z=(1,-2,3,-4,5,-6)i; camax(z) -> 6 camax(z:z*(1+i)) -> (6:8.48528137423857) ・同義 max(trans(abs(trans(z)))) -> 6 max(trans(abs(trans(z)),abs(trans(z*(1+i))))) -> (6:8.48528137423857) ・Ver.2.170.42以降、引数1個の場合、同じ引数を2個目に追加して正常化 camax(i) || camax(i,i) -> 1 ・Ver.2.170.42以降、NaNの引数に対応 camax(NaN) || camax(NaN,NaN) -> NaN |
|
目次
sqrt関数 入力仕様 |
sqrt関数の入力仕様と付随する留意事項について記述する
虚数単位 sqrt(-1) -> 6.123233995736766e-17+i ・Ver.2.184.44以降、auto-real selected時 sqrt(-1) -> NaN test caseを列挙する sqrt(2) -> 1.4142135623730951 sqrt(4) -> 2 sqrt(i) -> 0.7071067811865476+0.7071067811865475i sqrt(-1+eps*i) -> 6.123233995736766e-17+i sqrt(-1+MIN_VALUE*i) -> 6.123233995736766e-17+i |
|
目次
pow関数 入力仕様 |
pow関数の入力仕様と付随する留意事項について記述する
虚数単位 pow(-1,0.5) -> 6.123233995736766e-17+i ・Ver.2.184.44以降、auto-real selected時 pow(-1,0.5) -> NaN test caseを列挙する pow(2,2) -> 4 pow(2,4) -> 16 pow(i,4) -> 1-2.4492935982947064e-16i pow(2,i) -> 0.7692389013639721+0.6389612763136348i pow(-1+(eps)i,0.5) -> 6.123233995736766e-17+i pow(-1+(MIN_VALUE)i,0.5) -> 6.123233995736766e-17+i pow(2+MIN_VALUE*i,3) -> 7.999999999999998 詳細は演算子代替関数参照 |
|
目次
log関数 入力仕様 |
log関数の入力仕様と付随する留意事項について記述する
log関数の仕様はJavaScript準拠の自然対数とする log(e) -> 1 log(i) -> 1.5707963267948966i 底の変換 ・log(x)∝log10(x)∝log2(x) x=2; log(x) -> 0.6931471805599453 x=2; log10(x)/log10(e) -> 0.6931471805599453 x=2; log2(x)/log2(e) -> 0.6931471805599453 自然対数 ln(e) || log(e) -> 1 ln(10) || ln10() -> 2.302585092994046 ln(2) || ln2() -> 0.6931471805599453 ln(i) -> 1.5707963267948966i ・Ver.2.149.38以降、log関数の内部仕様を修正 ln(1/(-1)) || ln(1/(1-2)) -> 3.141592653589793i ln(-1) -> 3.141592653589793i ・Ver.2.184.44以降、auto-real selected時 ln(-1) -> NaN log(-1) -> NaN log(2) -> 0.6931471805599453 log(4) -> 1.3862943611198906 log(i) -> 1.5707963267948966i log(-1+i*eps) -> 3.141592653589793i log(-1-i*eps) -> -3.141592653589793i 常用対数 log10(10) -> 1 x=10; log(x)log10e() -> 1 x=100; log(x)log10e() -> 2 log10(i) -> 0.6821881769209206i 2進対数 Ver.2.89.32以降、追加 log2(2) -> 1 x=2; log(x)log2e() -> 1 x=4; log(x)log2e() -> 2 log2(i) -> 2.2661800709135966i Excel準拠log_ex(値,底||10) log_ex(10) || log_ex(10,10) -> 1 log_ex(e) || log10e() -> 0.43429448190325176 log_ex(e,2) || log2e() -> 1.4426950408889634 entropy∝ln(状態数) ・自然対数 ln(10**0) -> 0 ln(10**1) -> 2.302585092994046 ln(10**2) -> 4.605170185988092 ln(10**3) -> 6.907755278982137 ・N進法の桁数-1 N=10; log_ex(10**0,N) -> 0 N=10; log_ex(10**1,N) -> 1 N=10; log_ex(10**2,N) -> 2 N=10; log_ex(10**3,N) -> 2.9999999999999996 ・N進法の桁数(bit列長等、個数換算の+1を含む場合、状態数小で誤差大) N=10; log_ex(10**0,N)+1 -> 1 N=10; log_ex(10**1,N)+1 -> 2 N=10; log_ex(10**2,N)+1 -> 3 N=10; log_ex(10**3,N)+1 -> 3.9999999999999996 |
|
目次
atan2関数 入力仕様 |
atan2関数の入力仕様と付随する留意事項について記述する
atan2関数の仕様はJavaScript準拠の引数(y,x)とする atan2(1,0)/pi -> 0.5 deg_atan2(1,0) || degrees(atan2(1,0)) -> 90 ・不定の定義 atan2(0,0) -> 0 変数を使用 ・実軸と虚軸の複素数平面から弧度数radに変換する場合 z=e^(i{pi/6}); atan2(imag(z),real(z)) -> 0.5235987755982987 z=e^(i{pi/6}); arg(z) -> 0.5235987755982987 ・Ver.2.170.42以降、NaNの引数に対応 arg(NaN) -> NaN ・さらに、度数degに変換する場合 degrees(ans) || deg_atan2(imag(z),real(z)) -> 29.999999999999993 ・再度、弧度数radに変換 radians(ans) -> 0.5235987755982987 Excel準拠atan2_ex(x,y) atan2_ex(0,1)/pi -> 0.5 deg_atan2_ex(0,1) || degrees(atan2_ex(0,1)) -> 90 引数が-0の場合、留意事項を列挙する ・負から0に漸近を表す-0は未定義 x=-0,x -> (0,0) ・ただし、csv-formatの場合、-0が有効 ・Ver.2.151.38以降、実部の-0表示に対応 (-0,-0) -> (-0,-0) x=(-0),x -> (0,-0) ・次の場合、pi||2*piの特殊な数値誤差が残る atan2(0,-0) -> 3.141592653589793+O(3e+0) atan2(-0,-0) -> -3.141592653589793+O(3e+0) atan2(-0,-1) -> -3.141592653589793+O(6e+0) ・test caseを列挙する atan2(-0||0,-1) -> 3.141592653589793 atan2(-eps,-1) -> -3.141592653589793 atan2(eps,-1) -> 3.141592653589793 clear; y=-0; x=-1; atan2(y,x) -> 3.141592653589793 |
|
目次
三角関数 入力仕様 |
三角関数の入力仕様と付随する留意事項について記述する
三角関数 sin(z) cos(z) tan(z) 逆三角関数 asin(z) acos(z) atan(z) |
|
目次
双曲線関数 入力仕様 |
双曲線関数の入力仕様と付随する留意事項について記述する
双曲線関数 sinh(z) cosh(z) tanh(z) ・Ver.2.149.37以降、追加 csch(z) sech(z) coth(z) ・式変数の定義 sinh_(z)=<(exp(z)-exp(-z))/2; cosh_(z)=<(exp(z)+exp(-z))/2; tanh_(z)=<(exp(z)-exp(-z))/(exp(z)+exp(-z)); csch_(z)=<2/(exp(z)-exp(-z)); sech_(z)=<2/(exp(z)+exp(-z)); coth_(z)=<(exp(z)+exp(-z))/(exp(z)-exp(-z)); 逆双曲線関数 asinh(z) acosh(z) atanh(z) ・Ver.2.149.37以降、追加 acsch(z) asech(z) acoth(z) ・式変数の定義 asinh_(z)=<ln(sqrt(z*z+1)+z); acosh_(z)=<ln(sqrt(z*z-1)+z); atanh_(z)=<ln((1+z)/(1-z))/2; acsch_(z)=<asinh_(1/z); asech_(z)=<acosh_(1/z); acoth_(z)=<atanh_(1/z); |
|
目次
その他の関数 入力仕様 |
その他の関数の入力仕様と付随する留意事項について記述する
Kroneckerのdelta関数 Kdelta(0,0) -> 1 Kdelta(0,1) -> 0 Kdelta(1,0) -> 0 Kdelta(1,1) -> 1 Kdelta(2,2) -> 1 ・演算子代替関数を使用 Kdelta_(left,right)=<not(bitxor(left,right)); Kdelta_(left,right)=<eq(left,right); Kdelta_(0,0) -> 1 Kdelta_(0,1) -> 0 Kdelta_(1,0) -> 0 Kdelta_(1,1) -> 1 Kdelta_(2,2) -> 1 ・Ver.2.170.42以降、NaNの引数に対応 Kdelta(NaN) -> NaN Kdelta(NaN,1) -> NaN Kdelta(1,NaN) -> NaN |
|
目次
特殊仕様関数 入力仕様 |
特殊仕様関数の入力仕様と付随する留意事項について記述する
特殊仕様関数の定義を列挙する ・関数名の後に続く数字が引数に含まれる ・引数は関数call前に解決済み(未解決の変数名symbolを含む場合、予期せぬerror終了) 特殊仕様関数を列挙する ・統計関数のsort/reverse/csort/creverse関数 ・補間関数のinterp関数 |
|
目次
統計関数 入力仕様 |
統計関数の入力仕様と付随する留意事項について記述する
・Ver.2.90.32以降、mean/sum/prod関数を追加 ・Ver.2.91.32以降、median/sort/reverse/cmedian/csort/creverse関数を追加 ・Ver.2.128.34以降、sort/reverse/csort/creverse関数名直後の連番sort-key-i=0~を追加 ・Ver.2.304.77以降、median/sort/reverse/cmedian/csort/creverse関数の不具合を修正 clear; A=(1,(x)=<x); sort(A) -> sort0(5,1,4,2,2,3:=<x0,=<x1,=<x2,=<x3,=<x4,=<x5) -> ( 1,2,2,3,4,5: $x1,$x3,$x4,$x5,$x2,$x0 ) mean関数 ・各行vector要素の算術平均値 mean(1,1e-16) -> infoLost[r ] 0.5 mean(1,i) -> 0.5+0.5i mean(-1,-i) -> -0.5-0.5i mean(1,2,3:4,5,6) -> (2:5) mean(trans(mean(1,2,3:4,5,6))) -> 3.5 sum関数 ・各行vector要素の総和 sum(1,1e-16) -> infoLost[r ] 1 sum(1,i) -> 1+i sum(-1,-i) -> -1-i sum(1,2,3:4,5,6) -> (6:15) sum(trans(sum(1,2,3:4,5,6))) -> 21 prod関数 ・各行vector要素の総乗 prod(1,1e-16) -> 1e-16 prod(1,i) -> i prod(-1,-i) -> i prod(1,2,3:4,5,6) -> (6:120) prod(trans(prod(1,2,3:4,5,6))) -> 720 median関数 ・sort後中央値=各行vector[floor(vectorの長さ/2)]を参照 median(1,-2,3,-1:4,-5,6,-3:7) -> (1:4:7) median(1,-2i,3:4,-5,6i:7) -> (1:6i:7) ・列参照を使用 (sort(1,-2i,3:4,-5,6i:7))[][1] -> (1:6i:0) sort関数 ・実数昇順にBubble Sort sort(1,-2,3,-1:4,-5,6,-3:7) -> (-2,-1,1,3:-5,-3,4,6:7) sort(1,-2i,3:4,-5,6i:7) -> (-2i,1,3:-5,6i,4:7) sort(trans(1,-2i,3:4,-5,6i:7)) -> (1,4,7:-5,-2i,0:6i,0,3) ・Ver.2.128.34以降、欠損要素なしの行列table用に関数名直後の連番sort-key-i=0~を追加 table=(2,3,1:6,4,5); sort(table) -> (1,2,3:4,5,6) ・i=0(1行目)をkeyにsort sort0(table) -> (1,2,3:5,6,4) ・i=1(2行目)をkeyにsort sort1(table) -> (3,1,2:4,5,6) ・欠損要素が存在する場合、error終了 table=(2,3,1:6,4,5,7); sort0(table) -> [MyErr]Invalid table size sort0(trans(trans(table))) -> (0,1,2,3:7,5,6,4) ・key行が存在しない場合、error終了 sort2(table) -> [MyErr]Invalid table size ・無次元の演算も同様に、key有効の仕様とする table=(2,3,1:6,4,5); sort(table) -> (4,5,6) sort0(table) -> (5,6,4) sort1(table) -> (4,5,6) reverse関数 ・実数降順にBubble Sort reverse(1,-2,3,-1:4,-5,6,-3:7) -> (3,1,-1,-2:6,4,-3,-5:7) reverse(1,-2i,3:4,-5,6i:7) -> (3,1,-2i:4,6i,-5:7) reverse(trans(1,-2i,3:4,-5,6i:7)) -> (7,4,1:0,-2i,-5:3,0,6i) sort(reverse(1,-2i,3:4,-5,6i:7)) -> (-2i,1,3:-5,6i,4:7) ・area参照の反転参照を使用 (sort(1,-2i,3:4,-5,6i:7))[0][-1][][] -> (3,1,-2i:4,6i,-5:0,0,7) cmedian関数 ・csort後中央値=各行vector[floor(vectorの長さ/2)]を参照 cmedian(1,-2,3,-1:4,-5,6,-3:7) -> (-2:-5:7) cmedian(1,-2i,3:4,-5,6i:7) -> (-2i:-5:7) ・列参照を使用 (csort(1,-2i,3:4,-5,6i:7))[][1] -> (-2i:-5:0) csort関数 ・複素数の絶対値昇順にBubble Sort csort(1,-2,3,-1:4,-5,6,-3:7) -> (1,-1,-2,3:-3,4,-5,6:7) csort(1,-2i,3:4,-5,6i:7) -> (1,-2i,3:4,-5,6i:7) csort(trans(1,-2i,3:4,-5,6i:7)) -> (1,4,7:0,-2i,-5:0,3,6i) creverse関数 ・複素数の絶対値降順にBubble Sort creverse(1,-2,3,-1:4,-5,6,-3:7) -> (3,-2,-1,1:6,-5,4,-3:7) creverse(1,-2i,3:4,-5,6i:7) -> (3,-2i,1:6i,-5,4:7) creverse(trans(1,-2i,3:4,-5,6i:7)) -> (7,4,1:-5,-2i,0:6i,3,0) csort(creverse(1,-2i,3:4,-5,6i:7)) -> (1,-2i,3:4,-5,6i:7) ・area参照の反転参照を使用 (csort(1,-2i,3:4,-5,6i:7))[0][-1][][] -> (3,-2i,1:6i,-5,4:0,0,7) 留意事項を列挙する ・統計関数のalgorithmは未最適化 |
|
目次
補間関数 入力仕様 |
補間関数の入力仕様と付随する留意事項について記述する
Ver.2.176.43以降、線形補間のinterp関数を追加 ・Ver.2.178.44以降、lookup-table標本点の仕様変更 実部と虚部の各keyに対する各value(query困難) ⇒ 実数値keyに対する複素数value ・Ver.2.179.44以降、interp0/interp1関数を追加 ・Ver.2.181.44以降、interp2/interp3関数を追加 補間関数を列挙する ・interp0関数:最近傍補間 ・interp||interp1関数:線形補間 ・interp2関数:Lagrange補間 ・interp3関数:3次の自然spline補間 引数(x:table)の仕様を列挙する ・x:query点実数値の行vector(任意要素数のquery行) ・table:標本点{昇順key,value}の行vector(lookup-table行) key:実数値x(虚部は無視) value:複素数z=f(x) ・table-key範囲外の欠損値=NaN+(NaN)i 留意事項を列挙する ・table-key行が降順の場合、欠損値を返す interp(1.5:2,1:2,1) -> NaN ・table-key範囲外の場合、欠損値を返す(interp2関数を除く) interp(0:1,2:1,2) -> NaN ・table要素数不足の場合、欠損値を返す interp(1:1:1) -> NaN ・table要素数が不正の場合、error終了 interp(1:1,2:1,2,3) -> [MyErr]Invalid table(interp) interp(1:1,2:1,2:3) -> [MyErr]Invalid table(interp) |
|
目次
0次補間関数 入力仕様 |
0次補間関数の入力仕様と付随する留意事項について記述する
interp0(x:table)関数:実数値keyに対する複素数valueの最近傍補間 test caseを示す x=(-1,0,0.25,0.5,0.75,1,2); table=(0,1:1+i,2+3i); interp0(x:table) -> ( NaN,1+i,1+i,2+3i,2+3i,2+3i,NaN ) ・中間点は繰り上げる(四捨五入に同様) |
|
目次
1次補間関数 入力仕様 |
1次補間関数の入力仕様と付随する留意事項について記述する
interp||interp1(x:table)関数:実数値keyに対する複素数valueの線形補間 test caseを示す ・標本点の元data csv0=(1,2,5,4,3:-1,-2,-3,-4,-5); csv0 -> ( 1,2,5,4,3: -1,-2,-3,-4,-5 ) ・sort関数(虚部は無視)を使用して昇順sort csv0_sorted_key0=sort0(csv0); csv0_sorted_key0 -> ( 1,2,3,4,5: -1,-2,-5,-4,-3 ) ・lookup-tableを定義 table=csv0_sorted_key0*(1+i); table -> ( 1+i,2+2i,3+3i,4+4i,5+5i: -1-i,-2-2i,-5-5i,-4-4i,-3-3i ) ・query点を定義 x=(table[0]-(1+i)/2,table[0]+(1+i)/2); x -> ( 0.5+0.5i,1.5+1.5i,2.5+2.5i,3.5+3.5i,4.5+4.5i,1.5+1.5i,2.5+2.5i,3.5+3.5i,4.5+4.5i,5.5+5.5i ) ・Ver.2.178.44以降、同義 x=trans(real(trans(x))); x -> ( 0.5,1.5,2.5,3.5,4.5,1.5,2.5,3.5,4.5,5.5 ) ・補間を実行 interp(x:table) -> ( NaN,-1.5-1.5i,-3.5-3.5i,-4.5-4.5i,-3.5-3.5i,-1.5-1.5i,-3.5-3.5i,-4.5-4.5i,-3.5-3.5i,NaN ) ・table-key範囲外の場合、欠損値を返す interp(x:csv0_sorted_key0) -> ( NaN,-1.5,-3.5,-4.5,-3.5,-1.5,-3.5,-4.5,-3.5,NaN ) |
|
目次
n次補間関数 入力仕様 |
n次補間関数の入力仕様と付随する留意事項について記述する
interp2(x:table)関数:実数値keyに対する複素数valueのLagrange補間 ・補間多項式の性質上、table-key範囲外の外挿を許容する ・複素数演算の場合、plot2d_Lagrangeの演算結果とMachine epsilon程度の相違がある |
|
目次
3次補間関数 入力仕様 |
3次補間関数の入力仕様と付随する留意事項について記述する
interp3(x:table)関数:実数値keyに対する複素数valueの3次の自然spline補間 ・複素数演算の場合、plot2d_nsplineの演算結果とMachine epsilon程度の相違がある |
|
目次
特殊関数 入力仕様 |
特殊関数の入力仕様と付随する留意事項について記述する
特殊関数(非初等関数)は式変数と高階関数を使用して定義する ・標準正規分布SNDの確率密度関数(Ver.2.811.131以降、SND/P(x)/erf(x)/erfc(x)参照) SNDt=<exp(-t^2/2)/sqrt(2pi); SND(t)=<exp(-t^2/2)/sqrt(2*pi); ・SNDの累積分布関数P(x) Px=<_i((t)=<SNDt(),0,x)*2; P(x)=<_i((t)=<SND(t),0,x)*2; P(x)=<_i0((t)=<SND(t),0,x)*2; P(x)=<_o45((t,x)=<SND(t),,NI=100,x,NI)*2; ・誤差関数erf(x) erfx=<_i((t)=<SNDt(),0,x(sqrt2))*2; erf(x)=<P(x*sqrt2); ・同義 erfx=<_i((t)=<{exp(-t^2)},0,x)(2/sqrt(pi)); ・相補誤差関数erfc(x) erfcx=<1-erfx; erfc(x)=<1-erf(x); ・複素標準正規分布cSNDの確率密度関数(Ver.2.811.131以降、cSND/cP参照) cSND(z)=<exp(-abs(z)^2)/pi; ・cSNDの累積分布関数cP cP_z(z)=<_i((y)=<_i((x)=<cSND(x+(y)i)=>,0,real(z))*2,0,imag(z))*2; cP_r(r)=<_i((t)=<_i((r)=<cSND(r*e^(i*t))=>,0,r),0,2*pi)/sqrt(pi); ・正規化cP_r(r)=cP_z(r+abs(r)i)=erf(r) |
|
目次
行列 入力仕様 |
行列の入力仕様と付随する留意事項について記述する
vectorの入力方法2種類 ・各vectorの要素はcomma,で区切る 行vector(1,2) || [1,2] -> (1,2) 列vector{1,3} -> (1:3) 2行2列の行列の入力方法 1 2 3 4 ・各vectorはcolon:で区切る (1,2:3,4) || [1,2:3,4] || {1,3:2,4} -> (1,2:3,4) 行vector列挙指定の行列(以降、行指定の行列と呼ぶ) ((1,2):(3,4)) -> (1,2:3,4) ((1:2):(3:4)) -> (1:2:3:4) 列vector列挙指定の行列(以降、列指定の行列と呼ぶ) {{1,2}:{3,4}} || {1,2:3,4} -> (1,3:2,4) {{1:2}:{3:4}} || {1:2:3:4} -> (1,2,3,4) 行指定の行列と列指定の行列は互いに転置の関係 (1,2:3,4) -> (1,2:3,4) {1,2:3,4} -> (1,3:2,4) ・転置行列関数を使用 transpose({1,2:3,4}) || trans({1,2:3,4}) || trans{1,2:3,4} -> (1,2:3,4) ({1,2},{3:4}) || (trans(1,2),trans(3:4)) -> (1,3,4:2) ・1重列挙の場合、外側に括弧のassociativityは存在しない (1,2) || {(1,2)} || ({(1,2)}) || {({(1,2)})} -> (1,2) {1,2} || ({1,2}) || {({1,2})} || ({({1,2})}) -> (1:2) 2*(1,2) || {2*(1,2)} || ({2*(1,2)}) || {({2*(1,2)})} -> (2,4) {1,2}*2 || ({1,2}*2) || {({1,2}*2)} || ({({1,2}*2)}) -> (2:4) ・多重列挙の場合、vectorを括る括弧のassociativityに依存する {(1,2),(3:4)} -> (1,2:3:4) ({1,2}:{3:4}) || (trans(1,2):trans(3:4)) -> (1:2:3,4) 定義可能な行列演算 ・行列積 ・乗算記号*同様に積の記号*は省略可 (1,2:3,4)(1,2:3,4) -> (7,10:15,22) ・標準内積 (1,2,3){1,2,3} -> 14 ・Hermit内積 (1+i,1){1-i,1} -> 3 ・直積 {1,2,3}(1,2,3) -> (1,2,3:2,4,6:3,6,9) {1,2,3}(1,2) -> (1,2:2,4:3,6) {1-i,1}(1+i,1) -> (2,1-i:1+i,1) ・単位行列 k=1; (k,:,k) -> (1,0:0,1) ・scalar行列 k=-3; (k,:,k) -> (-3,0:0,-3) ・左右可換のscalar倍(同sizeのscalar行列との積) k=-3; (k,:,k)(1,2:3,4) || (1,2:3,4)(k,:,k) -> (-3,-6:-9,-12) ・Ver.2.88.32以降、定義できない乗算||減算||加算を拡張行列演算に追加 k=-3; k(1,2:3,4) || (1,2:3,4)k -> (-3,-6:-9,-12) ・符号 -(1,2:3,4) || (,:,)-(1,2:3,4) || (-1,:,-1)(1,2:3,4) -> (-1,-2:-3,-4) ・差 (1,2:3,4)-(1,2:3,4) -> (0,0:0,0) ・和 (1,2:3,4)+(1,2:3,4) -> (2,4:6,8) ・変数を使用 x=1; y=(x,2x:3x,4x); y*y-y || (7,10:15,22)-(1,2:3,4) -> (6,8:12,18) t=pi/4; (cos(t),sin(t):,){i(sin(t)),i(cos(t)):,} -> (i,0:0,0) 定義できない行列積の場合、error終了 ・Ver.2.88.32以降、定義できない乗算||減算||加算を拡張行列演算に追加 (1,2)(1,2) -> (1,4) 行列sizeの一致しない差と和の場合、error終了 ・Ver.2.88.32以降、定義できない乗算||減算||加算を拡張行列演算に追加 (1,2:3,4)-(-1,2) -> [MyErr]Invalid matrix operation (1,2:3,4)+(-1:) -> [MyErr]Invalid matrix operation (1,2:3,4)+(-1,2:,,) -> [MyErr]Invalid matrix operation A=(1,2:); A[0]+A[1] -> [MyErr]Invalid matrix operation (1,2:3,4)-(-1) -> (2,3:4,5) (1,2:3,4)-(-1,2) -> (2,0:4,2) (1,2:3,4)+(-1:) -> (0,1:3,4) (1,2:3,4)+(-1,2:,,) -> (0,4:3,4,4) A=(1,2:); A[0]+A[1] -> (1,2) A=(1,2:); ttA=trans(trans(A)); ttA[0]+ttA[1] -> (1,2) A=(1,2:,); A[0]+A[1] -> (1,2) 無次元の演算の場合、行列の演算規則とは無関係に最終要素を演算する (1,2:3)1 || (3)*1 -> 3 (1,2)/(3,4) || (2)/(4) -> 0.5 (1,2,3)+(4,5) || (3)+(5) -> 8 (1,2:3)-(4,5:6:7) || (3)-(7) -> -4 Ver.2.73.29以降、定義できない行列演算の場合、拡張行列演算参照 |
|
目次
欠損要素 入力仕様 |
欠損要素の入力仕様と付随する留意事項について記述する
・空要素と欠損要素を混同するため、本仕様は見直しの可能性がある 行列演算の欠損要素の扱い:欠損要素=空要素=0 ・test caseを列挙する (()) -> 0 (,) -> (0,0) (2,:)(1,2:3,4) || (2,:,)(1,2:3,4) -> (2,4:0,0) (1,2:3,4)(2,:) || (1,2:3,4)(2,:,) -> (2,0:6,0) (1,2,3:){1,2,3:} || (1,2,3:,,){1,2,3:,,} -> (14,0:0,0) ・転置行列関数を使用 trans(1,2,3:) -> (1,0:2,0:3,0) trans({1,2,3:}) -> (1,2,3:0,0,0) 欠損要素を埋めて行列sizeが一致する場合、差と和の演算を許容する (1,2:3,4)-(-1,:) || (1,2:3,4)-(-1,:,) || (1,2:3,4)-(-1,0:0,0) -> (2,2:3,4) (1,2:3,4)-(-1,2:) || (1,2:3,4)-(-1,2:,) || (1,2:3,4)-(-1,2:0,0) -> (2,0:3,4) (1,2:3,4)+(-1,:) || (1,2:3,4)+(-1,:,) || (1,2:3,4)+(-1,0:0,0) -> (0,2:3,4) (1,2:3,4)+(-1,2:) || (1,2:3,4)+(-1,2:,) || (1,2:3,4)+(-1,2:0,0) -> (0,4:3,4) 留意事項を列挙する ・欠損値の定義とは異なる |
|
目次
空行列 入力仕様 |
空行列の入力仕様と付随する留意事項について記述する
Ver.2.158.38以降、行列結合用の空行列を追加 ・Ver.2.170.41以降、列参照と列代入の[e]を空行列で代替可 Ver.2.747.112以降、列参照と列代入の[e]を廃止 ・角括弧[]を使用 [] -> [] [[]] -> [] [[[]]] -> [] x=[]; x -> [] 空行列を返す行列関数を列挙する ・初期化行列関数 test caseを示す test_concat(k0,N)=<[arr=[],_rk(=<last{arr=(arr,k),k+1},k0,N),=<arr]=>; vecr=test_concat(N=5,N)=>; vecr -> (0,1,2,3,4) sizer(vecr) -> 1 sizec(vecr) -> 5 留意事項を列挙する ・行列結合の前提 [],[] -> [] []:[] -> [] [],1,[]:1:[] -> (1:1) x=[]; (x,2),(2,x),{x,2},{2,x} -> (2,2,2,2) ・Ver.2.286.69以降、空行列との演算の場合、error終了を正常化 3*() || 3/() -> x=[]; 3*x || 3/x -> ・欠損要素 (,) -> (0,0) (:) -> (0:0) ・空括弧 ((),2) -> (0,2) x=(); (x,2) -> [MyErr]Invalid ans isFound ・任意要素への代入不可 clear; x=[]; x[0]=1 -> [MyErr]Invalid reference of array |
|
目次
定数扱いの 行列 入力仕様 |
定数扱いの行列の入力仕様と付随する留意事項について記述する
定数同様に扱う行列を列挙する vector2r || vector2r() -> (0,0) vector3r -> (0,0,0) vector4r -> (0,0,0,0) vector2c -> (0:0) vector3c -> (0:0:0) vector4c -> (0:0:0:0) zeros2 -> (0,0:0,0) zeros3 -> (0,0,0:0,0,0:0,0,0) zeros4 -> (0,0,0,0:0,0,0,0:0,0,0,0:0,0,0,0) ones2 -> (1,1:1,1) ones3 -> (1,1,1:1,1,1:1,1,1) ones4 -> (1,1,1,1:1,1,1,1:1,1,1,1:1,1,1,1) identity2 -> (1,0:0,1) identity3 -> (1,0,0:0,1,0:0,0,1) identity4 -> (1,0,0,0:0,1,0,0:0,0,1,0:0,0,0,1) |
|
目次
行列関数 入力仕様 |
行列関数の入力仕様と付随する留意事項について記述する
高階化しない行列関数の前提を列挙する ・引数は関数call前に解決済み 高階化しない行列関数の条件を列挙する ・引数が行列単体の場合 ・欠損要素なしの前提で複数の引数を行列結合する場合 |
|
目次
初期化 行列関数 入力仕様 |
行列を初期化する行列関数の入力仕様と付随する留意事項について記述する
・Ver.2.170.42以降、NaNの引数に対応 identity(NaN) -> [MyErr]Invalid matrix size 行vector vectorr(3.3) || vectorr(3) || vector3r -> (0,0,0) vectorr(6) -> (0,0,0,0,0,0) vectorr(9) -> (0,0,0,0,0,0,0,0,0) vectorr(-1) -> [MyErr]Invalid matrix size vectorr(1001) -> [MyErr]Invalid matSizeMax over ・Ver.2.185.44以降、行列size=0の場合、空行列を返す vectorr(0) -> [] 列vector vectorc(3) || vector3c -> (0:0:0) vectorc(6) -> (0:0:0:0:0:0) vectorc(9) -> (0:0:0:0:0:0:0:0:0) ・Ver.2.185.44以降、行列size=0の場合、空行列を返す vectorc(0) -> [] 単位行列 identity(3) -> (1,0,0:0,1,0:0,0,1) identity(5) -> (1,0,0,0,0:0,1,0,0,0:0,0,1,0,0:0,0,0,1,0:0,0,0,0,1) ・行列sizeは正の整数に identity(2.5) || identity(3) -> (1,0,0:0,1,0:0,0,1) identity(3.3) || identity(3) -> (1,0,0:0,1,0:0,0,1) ・行列sizeが負の場合、error終了 identity(-1) -> [MyErr]Invalid matrix size ・Ver.2.185.44以降、行列size=0の場合、空行列を返す identity(0) -> [] ・matSizeMaxを超過の場合、error終了 identity(1001) -> [MyErr]Invalid matSizeMax over ・出力logの文字数制限log.length<5000 identity(100) -> (1,0,0,...,0,0,0,... ・log表示負荷を下げる場合、変数に代入して括弧で括る (A=identity(100),A2=A*A) -> (0,0) scalar行列 scalars(2,-3) -> (-3,0:0,-3) scalars(3,i) -> (i,0,0:0,i,0:0,0,i) scalars(4,3-5i) -> (3-5i,0,0,0:0,3-5i,0,0:0,0,3-5i,0:0,0,0,3-5i) ・Ver.2.185.44以降、行列size=0の場合、空行列を返す scalars(0,1) -> [] ・任意size行列Aのscalar倍 ・Ver.2.88.32以降、定義できない乗算||減算||加算を拡張行列演算に追加 A=(1,2,3,4:5,6,7,8); scalars(sizer(A),2)*A || A*scalars(sizec(A),2) || A*2 || 2*A -> ( 2,4,6,8: 10,12,14,16 ) A={1,2,3,4:5,6,7,8}; scalars(sizer(A),2)*A || A*scalars(sizec(A),2) || A*2 || 2*A -> ( 2,10: 4,12: 6,14: 8,16 ) ・転置行列関数を使用 N=10; z=1+i; A=htrans(scalars(N,z))identity(N)scalars(N,z); A -> N=10; z=1+i; A=scalars(N,z)identity(N)htrans(scalars(N,z)); A -> ( 2,0,0,0,0,0,0,0,0,0: 0,2,0,0,0,0,0,0,0,0: 0,0,2,0,0,0,0,0,0,0: 0,0,0,2,0,0,0,0,0,0: 0,0,0,0,2,0,0,0,0,0: 0,0,0,0,0,2,0,0,0,0: 0,0,0,0,0,0,2,0,0,0: 0,0,0,0,0,0,0,2,0,0: 0,0,0,0,0,0,0,0,2,0: 0,0,0,0,0,0,0,0,0,2 ) zeros行列 zeros(2,2) -> (0,0:0,0) zeros(3,5) -> (0,0,0,0,0:0,0,0,0,0:0,0,0,0,0) zeros(-1,1) -> [MyErr]Invalid matrix size zeros(1001,1) -> [MyErr]Invalid matSizeMax over ・band代入を使用 mat3x3=zeros(3,3); pivot=1; mat3x3[0][0][0]=(pivot,pivot,pivot); mat3x3 -> ( 1,0,0: 0,1,0: 0,0,1 ) ・Ver.2.185.44以降、正方行列の場合、第2引数を省略可 zeros(NaN) -> [MyErr]Invalid matrix size zeros(1) -> 0 zeros(2) -> (0,0:0,0) zeros(3) -> (0,0,0:0,0,0:0,0,0) ・Ver.2.185.44以降、行列size=0の場合、空行列を返す zeros(0) || zeros(0,1) || zeros(1,0) -> [] ones行列 ones(2,2) -> (1,1:1,1) ones(5,3) -> (1,1,1:1,1,1:1,1,1:1,1,1:1,1,1) ・Ver.2.185.44以降、正方行列の場合、第2引数を省略可 ones(NaN) -> [MyErr]Invalid matrix size ones(1) -> 1 ones(2) -> (1,1:1,1) ones(3) -> (1,1,1:1,1,1:1,1,1) ・Ver.2.185.44以降、行列size=0の場合、空行列を返す ones(0) || ones(0,1) || ones(1,0) -> [] |
|
目次
space 初期化 行列関数 入力仕様 |
spaceを初期化する行列関数の入力仕様と付随する留意事項について記述する
Ver.2.183.44以降、linspace関数を追加 ・Ver.2.228.55以降、整数の丸め方を最適化 引数(a,b,opt_Np1)の仕様を列挙する ・[a,b]:複素数valueの区間 ・opt_Np1||50:区間分割数N+1の離散点数 linspace(a,b,opt_Np1)関数:linear-scaleの初期化 ・test caseを列挙する linspace(0,5,6):linspace(0,5,6)**2 -> (0,1,2,3,4,5:0,1,4,9,16,25) linspace(1+2i,10+10i,9) -> (1+2i,2.125+3i,3.25+4i,4.375+5i,5.5+6i,6.625+7i,7.75+8i,8.875+9i,10+10i) linspace(10+10i,1+2i,9) -> (10+10i,8.875+9i,7.75+8i,6.625+7i,5.5+6i,4.375+5i,3.25+4i,2.125+3i,1+2i) ・複数行の初期化 linspace(0,5,6:0,5,6) -> (0,1,2,3,4,5:0,1,2,3,4,5) linspace(0,5,6:0,10,11) -> (0,1,2,3,4,5:0,1,2,3,4,5,6,7,8,9,10) ・行列size=1の場合、区間下端を返す linspace([2,3],1) || linspace(2,3,1) -> 2 ・行列size=0の場合、error終了 linspace(1,2,0) -> [MyErr]Invalid matrix size linspace(1,2,NaN) -> [MyErr]Invalid matrix size linspace(1,2,1001) -> [MyErr]Invalid matSizeMax over linspace(1) -> [MyErr]Invalid args.length=2||3(linspace) linspace(1,NaN,2) -> (NaN,NaN) args=(trans(linspace(2,2,4)),trans(linspace(1,4,4))); pow(args) -> (2:4:7.999999999999998:15.999999999999998) ・Ver.2.184.44以降、auto-real selected時 args=(trans(linspace(2,2,4)),trans(linspace(1,4,4))); pow(args) -> (2:4:8:16) N=8; pow(trans(linspace(2,2,N:1,N,N))) -> (2:4:8:16:32:64:128:256) 留意事項を列挙する ・整数の丸め方 round(linspace(1,1000,1000).). linspace(1,1000,1000).map((x)=<round(x)) ・Ver.2.228.55以降、対策済み(round不要) linspace(1,1000,1000) |
|
目次
isFalse /isTrue 行列関数 入力仕様 |
isFalse/isTrue行列関数の入力仕様と付随する留意事項について記述する
Ver.2.172.42以降、isFalse/isTrue行列関数を追加 isFalse行列関数 ・引数がfalse判定値を判定 isFalse(false),isFalse(true),isFalse(NaN) -> (true,false,true) isFalse(0),isFalse(1),isFalse(i) -> (true,false,false) isFalse(false,false),isFalse(NaN,NaN),isFalse(,) -> (false,false,false) ・実数演算 isFalse(false),isFalse(true),isFalse(NaN) -> (true,false,true) isFalse(0),isFalse(1),isFalse(i) -> (true,false,true) isFalse(false,false),isFalse(NaN,NaN),isFalse(,) -> (false,false,false) isTrue行列関数 ・引数がtrue判定値を判定 isTrue(false),isTrue(true),isTrue(NaN) -> (false,true,false) isTrue(0),isTrue(1),isTrue(i) -> (false,true,true) isTrue(false,false),isTrue(NaN,NaN),isTrue(,) -> (true,true,true) ・実数演算 isTrue(false),isTrue(true),isTrue(NaN) -> (false,true,false) isTrue(0),isTrue(1),isTrue(i) -> (false,true,false) isTrue(false,false),isTrue(NaN,NaN),isTrue(,) -> (true,true,true) 留意事項を列挙する ・論理値literalを返す |
|
目次
転置 行列関数 入力仕様 |
転置行列関数の入力仕様と付随する留意事項について記述する
・Ver.2.192.44以降、dot演算子を追加 行列の非共役転置 trans(1,2:3,4) -> (1,3:2,4) trans(1,2i:3,4i:-5i) -> (1,3,-5i:2i,4i,0) ・行vectorを列vectorに変換 transpose(1,2,3) || trans(1,2,3) -> (1:2:3) ・列vectorを行vectorに変換 trans({1,2,3}) || trans{1,2,3} -> (1,2,3) 複素数の行列の共役転置(Hermit転置) htrans(1-i,1-2i:1-3i,1-4i) || Hermitian(1-i,1-2i:1-3i,1-4i) -> (1+i,1+3i:1+2i,1+4i) htrans(1,2i:3,4i:-5i) -> (1,3,5i:-2i,-4i,0) |
|
目次
last 行列関数 入力仕様 |
last行列関数の入力仕様と付随する留意事項について記述する
行列要素を取得 ・最初要素(行列の最初行の最初列の要素) first(1,2:3,4) -> 1 first{1,2:3,4} -> 1 ・最終要素(行列の最終行の最終列の要素) last(1,2:3,4) -> 4 last{1,2:3,4} -> 4 ・単位tree構造の仕様上、行vectorの欠損要素を自動で埋めない A=(1,2:3,(,:,4),5); A -> ( 1,2: 3,0,0,5: ) ・Ver.2.156.38以降、irregular行列の行列結合の仕様変更 last(A) -> 4 last(trans(trans(A))) -> 0 last行列関数はNativeのcomma演算子同様に、括弧内の最終要素を返す ・同じ括弧でcomma,を括る場合 last((1,2):(3,4)) -> 4 last{{1,2}:{3,4}} -> 4 ・colon:を含めて括る場合、意図とは異なる可能性あり ・最終列挙の要素が最終要素とは限らない (1,(2:3),4) -> ( 1,2,4: ) ・Ver.2.156.38以降、irregular行列の行列結合の仕様変更 last(1,(2:3),4) -> 3 ・括弧を統一しない場合、意図とは異なる可能性あり ({1,2},3,4) -> ( 1,3,4: 2 ) last({1,2},3,4) -> 2 最終列挙の要素を取得する場合 ・常にlast行列関数で括弧内の最終要素を取り出す last(1,last(2:3),4) -> 4 last(last{1,2},3,4) -> 4 last(last(last{1,2},3),4) -> 4 last(last(1,2),last(3,4)) -> 4 last(last(1,2),last(3:4)) -> 4 last(last(1,2),last{3:4}) -> 4 last(last{1,2},last(3:4)) -> 4 last(last{1,2},last{3:4}) -> 4 last(last{1,2}:last{3:4}) -> 4 ・仕様上、変数への代入は次元を残さず、無次元の0を返す (vc={1,2,3},vr=(1,2,3),normc(vc)) -> (0,0,3.7416573867739413) last(ans) -> 3.7416573867739413 ・次元を残した場合(参考) ({0,0,0},(0,0,0),1) -> (0,0,0,0,1:0:0) (last{0,0,0},last(0,0,0),1) -> (0,0,1) |
|
目次
size 行列関数 入力仕様 |
size行列関数の入力仕様と付随する留意事項について記述する
m行n列の行列size(欠損要素を自動で埋める) ・Ver.2.185.44以降、size行列関数の非正方行列の返値の仕様変更(n ⇒ {m,n}) size(1,2:3,4) -> 2 size(1,2:3,4:) -> (3:2) ・行size:=m sizer(1,2:3,4) -> 2 sizer(1,2:3,4)[0] || sizer(1,2) -> 1 sizer(1:3,4) -> 2 sizer(1:3,4:) -> 3 ・列size:=n sizec(1,2:3,4) -> 2 sizec(1,2:3,4)[0] || sizec(1,2) -> 2 sizec(1,2:3) -> 2 sizec(1,2:3:4,5,) -> 3 ・Ver.2.280.66以降、未定義の変数をoperation段階で検知するため、error終了 clear; sizer(a,b:c,d) || sizer(,:,) -> 2 clear; sizec(a,b:c,d) || sizec(,:,) -> 2 ・定義済み変数を含む場合 clear; A=(,:,); sizer(A,b:c,d) || sizer(A,:,) -> 3 clear; A=(,:,); sizec(A,b:c,d) || sizec(A,:,) -> 3 clear; A=(,:,); sizer(A,b:c,A) || sizer(A,:,A) -> 4 clear; A=(,:,); sizec(A,b:c,A) || sizec(A,:,A) -> 3 clear; A=(,:,); sizer(A,A:A,A) -> 4 clear; A=(,:,); sizec(A,A:A,A) -> 4 test caseを示す size(1) -> 1 size(identity(2)) -> 2 size(zeros(2,3)) -> (2:3) size_mn(mat)=<{sizer(mat),sizec(mat)}; mat=(1,2:3,4:5,6); size(mat) -> (3:2) size_mn(=<mat) -> (3:2) {$m,$n}=size_mn(=<mat); (m,n) -> (3,2) =((size_mn(=<mat))[0],(size_mn(=<mat))[1]) -> (3,2) |
|
目次
reshape 行列関数 入力仕様 |
reshape行列関数の入力仕様と付随する留意事項について記述する
Ver.2.234.56以降、reshaper/reshape/reshapec行列関数を追加 ・Ver.2.240.56以降、既定形式の仕様変更 reshape:reshapec ⇒ reshaper(列vector形式 ⇒ 行vector形式) ・Ver.2.825.139以降、reshapez行列関数を追加 留意事項を列挙する ・行列要素の参照を再配置して返す(参照非共有) |
|
目次
norm 行列関数 入力仕様 |
norm行列関数の入力仕様と付随する留意事項について記述する
Ver.2.187.44以降、normr/norm/normc行列関数を追加して返値の仕様変更 ・最終行/最終列vectorのnorm ⇒ 各行/各列vectorのnorm(正規化行列関数に準拠) ・Ver.2.240.56以降、既定形式の仕様変更 norm:normc ⇒ normr(列vector形式 ⇒ 行vector形式) 各行vectorのEuclidean norm(vectorの長さ) normr(1,2,3) || norm(1,2,3) || euclidean(1,2,3) -> 3.7416573867739413 normr(NaN) -> NaN ・行vector形式の連立方程式x*A=bのnorm(x)想定 normr(-i,2i,-3i) -> 3.7416573867739413 mat=(1,2:3,4); normr(mat),normr(mat[1]),normr(3,4) -> (5,5,5) ・行列の場合 mat=(1,2:3,4); normr(mat) -> (2.23606797749979:5) ・正規化の拡張行列演算 mat=(4,3i:-3,4i); mat/normr(mat) -> (0.8,0.6i:-0.6,0.8i) 各列vectorのEuclidean norm(vectorの長さ) normc(1:2:3) -> 3.7416573867739413 normc(NaN) -> NaN ・列vector形式の連立方程式A*x=bのnorm(x)想定 normc(1:2:3) || normc{1,2,3} || normc({1,2,3}) -> 3.7416573867739413 normc(-i:2i:-3i) || normc{-i,2i,-3i} || normc({-i,2i,-3i}) -> 3.7416573867739413 normc((1-i)/sqrt2:2i:-3i) || normc({(1-i)/sqrt2,2i,-3i}) -> 3.7416573867739413 x=((1-i)/sqrt2,2i,-3i); normc(trans(x)) -> 3.7416573867739413 ・有次元の場合、同義 x=((1-i)/sqrt2,2i,-3i); sqrt(x*htrans(x)) -> 3.7416573867739413 x={(1-i)/sqrt2,2i,-3i}; sqrt(htrans(x)x) -> 3.7416573867739413 ・Hermit内積 x=((1-i)/sqrt2,2i,-3i); x*htrans(x) -> 14 x={(1-i)/sqrt2,2i,-3i}; htrans(x)x -> 14 ・標準内積 x={(1-i)/sqrt2,2i,-3i}; trans(x)x -> -13-0.9999999999999998i ・よって複素数の場合、非同義 x={(1-i)/sqrt2,2i,-3i}; abs(sqrt(trans(x)x)) // NG -> 3.6108731368472777 normc((1-i)/sqrt2,2i,-3i) || normc(-3i) // NG -> 3 ・行列を指定した場合、最終列を参照 mat={1,2:3,4}; normc(mat),normc(mat[][1]),normc(3:4),normc{3,4},normc({3,4}),normc{{3,4}} -> (5,5,5,5,5,5) ・行列の場合 mat={1,2:3,4}; normc(mat) -> (2.23606797749979,5) ・正規化の拡張行列演算 mat={4,3i:-3,4i}; mat/normc(mat) -> (0.8,-0.6:0.6i,0.8i) |
|
目次
正規化 行列関数 入力仕様 |
正規化行列関数の入力仕様と付随する留意事項について記述する
各行vectorの正規化 ・Ver.2.240.56以降、既定形式の仕様変更 normalize:normalizec ⇒ normalizer(列vector形式 ⇒ 行vector形式) vr=(1,i,-i); normalizer(vr) || normalize(vr) -> (0.5773502691896258,0.5773502691896258i,-0.5773502691896258i) normc(trans(normalizer(vr))) ・同義 ・行vectorの左からnormの逆数を積 ・転置行列関数を使用 vr=(1,i,-i); (1/normc(trans(vr)))vr -> (0.5773502691896258,0.5773502691896258i,-0.5773502691896258i) ・zeros-vectorの場合、不定としてNaNを返す normalizer(0,0,0) // NG -> (NaN,NaN,NaN) ・行列の場合 A=(1:1,i:1,i,-i); A -> (1:1,i:1,i,-i) normalizer(A) -> (1,0,0: 0.7071067811865475,0.7071067811865475i,0: 0.5773502691896258,0.5773502691896258i,-0.5773502691896258i) ・各行vectorを行列操作で正規化する場合 ・転置行列関数を使用 (1/normc(trans(A[0])))A[0] -> 1 (1/normc(trans(A[1])))A[1] -> (0.7071067811865475,0.7071067811865475i) (1/normc(trans(A[2])))A[2] -> (0.5773502691896258,0.5773502691896258i,-0.5773502691896258i) 各列vectorの正規化 vc={1,i,-i}; normalizec(vc) -> (0.5773502691896258:0.5773502691896258i:-0.5773502691896258i) ・同義 ・列vectorの右からnormの逆数を積 vc={1,i,-i}; vc(1/normc(vc)) -> (0.5773502691896258:0.5773502691896258i:-0.5773502691896258i) ・行vectorを誤入力した場合 vr=(1,i,-i); normalizec(vr) // NG -> (1,i,-i) ・zeros-vectorの場合、不定としてNaNを返す normalizec({0,0,0}) // NG -> (NaN:NaN:NaN) ・行列の場合 tA={1:1,i:1,i,-i}; tA -> (1,1,1:0,i,i:0,0,-i) normalizec(tA) -> (1,0.7071067811865475,0.5773502691896258: 0,0.7071067811865475i,0.5773502691896258i: 0,0,-0.5773502691896258i) ・各列vectorを行列操作で正規化する場合 ・転置行列関数を使用 tA={1:1,i:1,i,-i}; A=trans(tA); A -> (1,0,0:1,i,0:1,i,-i) trans((1/normc(trans(A[0])))A[0]) -> (1:0:0) trans((1/normc(trans(A[1])))A[1]) -> (0.7071067811865475:0.7071067811865475i:0) trans((1/normc(trans(A[2])))A[2]) -> (0.5773502691896258:0.5773502691896258i:-0.5773502691896258i) |
|
目次
座標形式 行列関数 入力仕様 |
座標形式行列関数の入力仕様と付随する留意事項について記述する
Ver.2.123.34以降、疎行列を扱う座標形式(以降、COO形式と呼ぶ)の行列関数を追加 Ver.2.124.34以降、memory使用量と演算量=Order(N^3)の削減のため、COO形式のGaussの消去法を追加 ・ただし、演算量より要素探索の制御文がneckでthroughputは低い ・Ver.2.128.35以降、pivot選択でのerror終了を修正(pivot=0でも通るように) ・Ver.2.135.35以降、制御文低減のため、COO形式⇒LIL形式の変換処理を追加(Gauss関数の完全互換) ・Ver.2.217.50以降、欠損値の場合、NaNを返す COO形式の行列からm行n列の行列を復元 ・COO行列:=(aA:mA:nA) clear; aA=(1); mA=(1); nA=(2); coo=(aA:mA:nA); A=coo2mat(coo); A -> (0,1) clear; aA=(1,1+i,1-i); mA=(1,2,3); nA=(1,2,3); coo=(aA:mA:nA); A=coo2mat(coo); A -> ( 1,0,0: 0,1+i,0: 0,0,1-i ) clear; aA=(1,1+i,1-i); mA=(1,2,3); nA=(1,4,3); coo=(aA:mA:nA); A=coo2mat(coo); A -> ( 1,0,0,0: 0,0,0,1+i: 0,0,1-i,0 ) clear; aA=(1,1+i,1-i); mA=(1,2,3); nA=(1,2,3); coo=(aA:mA:2*nA); A=coo2mat(coo); A -> ( 0,1,0,0,0,0: 0,0,0,1+i,0,0: 0,0,0,0,0,1-i ) ・重複定義の場合、 clear; aA=(1,1+i,1-i); mA=(1,2,1); nA=(1,4,1); coo=(aA:mA:nA); A=coo2mat(coo); A -> [MyErr]Invalid duplication of coo 1-i,0,0,0: 0,0,0,1+i ) ・引数不正の場合、error終了 clear; aA=(1,1+i,1-i); mA=(1,2,3); nA=(1,2,3); coo=(aA:mA); A=coo2mat(coo); A -> [MyErr]Invalid coo2matSize clear; aA=(1,1+i); mA=(1,2,3); nA=(1,2,3); coo=(aA:mA:nA); A=coo2mat(coo); A -> [MyErr]Invalid coo2matSize clear; aA=(1,1+i:1-i); mA=(1,2,3); nA=(1,2,3); coo=(aA:mA:nA); A=coo2mat(coo); A -> [MyErr]Invalid coo2matSize ・行列sizeの制限によるerror終了 clear; aA=(1,1+i,1-i); mA=(0,2,3); nA=(1,2,3); coo=(aA:mA:nA); A=coo2mat(coo); A -> [MyErr]Invalid matrix size clear; aA=(1,1+i,1-i); mA=(1001,2,3); nA=(1,2,3); coo=(aA:mA:nA); A=coo2mat(coo); A -> [MyErr]Invalid matSizeMax over ・Ver.2.126.34以降、逆変換を追加 clear; A=(1,2,:3,4,:,,,); mat2coo(A) -> ( 1,2,3,4: 1,1,2,2: 1,2,1,2 ) clear; A=(1,2,:3,4,:,,,); cA=mat2coo(A); aA=cA[0]; mA=cA[1]; nA=cA[2]; aA -> (1,2,3,4) mA -> (1,1,2,2) nA -> (1,2,1,2) ・数値誤差のみの要素を保持する clear; num0=_dx(=<{1},1,); mcA=coo2mat(mat2coo(1,2,num0:3,4:5,,)); mcA -> ( 1,2,0+O(1e-12+1e-12i): 3,4,0 5,0,0 ) ・Ver.2.170.42以降、NaNの引数に対応 ・Ver.2.217.50以降、NaNを返す mat2coo(NaN) || mat2coo(0) -> (NaN:NaN:NaN) COO形式のGaussの消去法 aA=(1,2,3); mA=(1,2,3); nA=(1,2,3); b={4,5,6}; coo=(aA:mA:nA); x=Gauss_coo(aA:mA:nA:trans(b)); x -> (4:2.5:2) x=Gauss_coo(1,2,3:1,2,3:1,2,3:4,5,6); x -> (4:2.5:2) ・要素の順序を任意に交換可 aA=(3,1,2); mA=(3,1,2); nA=(3,1,2); coo=(aA:mA:nA); b={4,5,6}; x=Gauss_coo(coo:trans(b)); x -> (4:2.5:2) ・Ver.2.128.34以降、COO行列のi=1(2行目のmA)をkeyにsort clear; aA=(3,1,2); mA=(3,1,2); nA=(3,1,2); coo=(aA:mA:nA); coo_sorted=sort1(coo); coo_sorted -> (1,2,3:1,2,3:1,2,3) ・Aとbの行列size不一致の場合、error終了 clear; aA=(1,2,3); mA=(1,2,3); nA=(1,2,3); b={4,5}; coo=(aA:mA:nA); x=Gauss_coo(coo:trans(b)); x -> [MyErr]Invalid coo2matSize ・定義不正の場合、error終了 clear; aA=(1,2,3); mA=(2,2,3); nA=(1,2,3); b={4,5,6}; coo=(aA:mA:nA); x=Gauss_coo(coo:trans(b)); x -> [MyErr]Invalid gauss_coo2mat ・test caseを示す aA=(1,1,-2,1+i,3i,1,1-i,-1,-i); mA=(1,1,2,2,2,3,3,4,4); nA=(1,2,1,2,3,1,3,3,4); coo=(aA:mA:nA); b={4,5,6,7i}; x=Gauss_coo(coo:trans(b)); x -> ( 2.0588235294117645+5.235294117647058i: 1.9411764705882355-5.235294117647059i: 4.588235294117647-0.6470588235294115i: -6.352941176470589+4.588235294117647i ) ・double-check A=coo2mat(coo); x-Gauss(A,b) -> (0,0,0,0) A*x -> ( 4-8.881784197001252e-16i: 5+1.7763568394002505e-15i: 6: 7i ) 留意事項を列挙する ・COO形式のみ行列sizeの連番を使用(行列への参照は行列indexの連番を使用) Ver.2.130.35以降、COO形式の挙動を確認する場合、[test]solver参照 |
|
目次
行列操作 入力仕様 |
行列操作の入力仕様と付随する留意事項について記述する
行列への参照方法を列挙する ・行列size ・行列index ・行参照 ・列参照 ・要素参照 ・area参照 ・band参照 行列への代入方法を列挙する ・行代入 ・列代入 ・要素代入 ・area代入 ・band代入 |
|
目次
行列への参照 入力仕様 |
行列への参照の入力仕様と付随する留意事項について記述する
行列への参照は角括弧[]で指定する 行列への参照方法を列挙する ・行参照 ・列参照 ・要素参照 ・area参照 ・band参照 |
|
目次
行列size 入力仕様 |
行列sizeの入力仕様と付随する留意事項について記述する
m行n列の行列の行列sizeを定義する 行size:=m=1~matSizeMax 列size:=n=1~matSizeMax |
|
目次
行列index 入力仕様 |
行列indexの入力仕様と付随する留意事項について記述する
m行n列の行列の行列indexを定義する(以降、ij参照の行列と呼ぶ) 行index:=i=0~m-1 列index:=j=0~n-1 ・Ver.2.747.112以降、行列indexの判別を厳格化 A=(1,2:3,4); A[i] -> |
|
目次
行参照 入力仕様 |
行参照の入力仕様と付随する留意事項について記述する
Ver.2.78.31以降、行列の行参照と行代入の反転機能を追加 行参照 行列[行index] 変数[行index] 式変数[行index]=> 式変数[行index](arguments)=> ・行vectorを参照する場合、1個の角括弧[]で行indexを指定する A=(1,2:3,4); A[0] || (1,2:3,4)[0] -> (1,2) A=(1,2:3,4); A[1] || (1,2:3,4)[1] -> (3,4) ・以降、式変数を使用 A=<(1,2:3,4); A[0]=> -> (1,2) A=<(1,2:3,4); A[1]=> -> (3,4) A(t)=<(t,2t:3t,4t)[0]; A(-1)=> || (A(-1)=>)[0]; -> (-1,-2) A(t)=<(t,2t:3t,4t)[1]; A(-1)=> || (A(-1)=>)[0]; -> (-3,-4) A(t)=<(t,2t:3t,4t); A[0](-1)=> || (A(-1)=>)[0] -> (-1,-2) A(t)=<(t,2t:3t,4t); A[1](-1)=> || (A(-1)=>)[1] -> (-3,-4) A(t)=<(t,2t:3t,4t); A(-1)=>[1] -> [MyErr]Invalid REe(=>) A(t)=<(t,2t:3t,4t); A(-1)[1]=> -> [MyErr]Invalid reference of array ・欠損要素を自動で埋めない A=<(1:3,4); A[0]=> -> 1 A=<(1:3,4); A[1]=> -> (3,4) ・行indexが負の場合、反転参照を定義する A=<(1:3,4:); A[-1]=> -> 0 A=<(1:3,4:); A[-2]=> -> (3,4) A=<(1:3,4:); A[-3]=> -> 1 ・未定義の行列要素の参照不可 A=<(1:3,4:); A[-4]=> -> [MyErr]Invalid reference of array A=<(1:3,4:); A[3]=> -> [MyErr]Invalid reference of array A=<(1:3,4:); A[0.3]=> -> [MyErr]Invalid reference of array |
|
目次
列参照 入力仕様 |
列参照の入力仕様と付随する留意事項について記述する
Ver.2.76.29以降、行列の列参照と列代入を追加 ・Ver.2.78.31以降、行列の列参照と列代入の反転機能を追加 ・Ver.2.79.31以降、行index=-1 ⇒ Napier数eに演算仕様変更 ・Ver.2.170.41以降、列参照の[e]を空行列で代替可 Ver.2.747.112以降、列参照と列代入の[e]を廃止 列参照 行列[e][列index] 変数[e][列index] 式変数[e][列index]=> 式変数[e][列index](arguments)=> ・列vectorを参照する場合、2個の角括弧[]で行indexにNapier数e||空行列を指定する A=(1,2:3,4); A[][0] || (1,2:3,4)[][0] -> (1:3) A=(1,2:3,4); A[e][0] || (1,2:3,4)[e][0] -> (1:3) A=(1,2:3,4); A[e][1] || (1,2:3,4)[e][1] -> (2:4) ・欠損要素を自動で埋める A=(1:3,4); A[e][1] || (1:3,4)[e][1] -> (0:4) A=(1:3,4:); A[e][1] || (1:3,4)[e][1] -> (0:4:0) A=(1:3,4:); A[e][0] || (1:3,4)[e][0] -> (1:3:0) ・同義 get_vectorc(A,ic)=<trans((trans(A))[ic]); A=(1:3,4:); get_vectorc(=<A,0) -> (1:3:0) A=(1:3,4:); get_vectorc(=<A,1) -> (0:4:0) ・未定義の行列要素の参照不可 A=(1:3,4:); get_vectorc(=<A,2) -> [MyErr]Invalid reference of array A=(1:3,4:); A[e][2] || (1:3,4)[e][2] -> [MyErr]Invalid reference of array(column) A=(1:3,4:); A[e][0.3] || (1:3,4)[e][0.3] -> [MyErr]Invalid reference of array(column) ・列indexが負の場合、反転参照を定義する A=(1,2:3,4); A[e][-1] || (1,2:3,4)[e][-1] -> (2:4) A=(1,2:3,4); A[e][-2] || (1,2:3,4)[e][-2] -> (1:3) A=(1,2:3,4); A[e][-3] || (1,2:3,4)[e][-3] -> [MyErr]Invalid reference of array(column) ・転置行列関数を使用 A=(1,2:3,4); trans((trans(A))[1]) || htrans((htrans(A))[1]) -> (2:4) A=(i,2i:3i,4i); trans((trans(A))[1]) || htrans((htrans(A))[1]) -> (2i:4i) trans((trans(1,2:3,4))[1]) || htrans((htrans(1,2:3,4))[1]) -> (2:4) trans((trans(i,2i:3i,4i))[1]) || htrans((htrans(i,2i:3i,4i))[1]) -> (2i:4i) ・括弧は関数より優先するため、関数の外側を上位の括弧で括る A=(1,2:3,4); (trans(A))[1] // OK -> (2,4) (trans(1,2:3,4))[1] // OK -> (2,4) A=(1,2:3,4); trans(A)[1] || trans((A)[1]) // NG -> (3:4) trans(1,2:3,4)[1] || trans((1,2:3,4)[1]) // NG -> (3:4) |
|
目次
要素参照 入力仕様 |
要素参照の入力仕様と付随する留意事項について記述する
要素参照 行列[行index][列index] 変数[行index][列index] 式変数[行index][列index]=> 式変数[行index][列index](arguments)=> ・行列要素を参照する場合、2個の角括弧[]で行/列indexを指定する A=(1,2:3,4); A[0][0] || (1,2:3,4)[0][0] -> 1 A=(1,2:3,4); A[0][1] || (1,2:3,4)[0][1] -> 2 A=(1,2:3,4); A[1][0] || (1,2:3,4)[1][0] -> 3 A=(1,2:3,4); A[1][1] || (1,2:3,4)[1][1] -> 4 ・任意要素を演算 (1,2:3,4)[0][0]3 || 1*3 -> 3 (1)[0][0]3=(x=3) || 1*3=0 -> -3 ・以降、式変数を使用 A=<(1,2:3,4); A[0][0]=> -> 1 A=<(1,2:3,4); A[0][1]=> -> 2 A=<(1,2:3,4); A[1][0]=> -> 3 A=<(1,2:3,4); A[1][1]=> -> 4 A(t)=<(t,2t:3t,4t); A[0][0](-1)=> || (A(-1)=>)[0][0] -> -1 A(t)=<(t,2t:3t,4t); A[0][1](-1)=> || (A(-1)=>)[0][1] -> -2 A(t)=<(t,2t:3t,4t); A[1][0](-1)=> || (A(-1)=>)[1][0] -> -3 A(t)=<(t,2t:3t,4t); A[1][1](-1)=> || (A(-1)=>)[1][1] -> -4 A(t)=<(t,2t:3t,4t)[0]; A[0][0](-1)=> || (A(-1)=>)[0][0] -> -1 A(t)=<(t,2t:3t,4t)[0]; A[0][1](-1)=> || (A(-1)=>)[0][1] -> -2 A(t)=<(t,2t:3t,4t)[0]; A[1][0](-1)=> || (A(-1)=>)[1][0] -> [MyErr]Invalid reference of array A(t)=<(t,2t:3t,4t)[1]; A[0][0](-1)=> || (A(-1)=>)[0][0] -> -3 A(t)=<(t,2t:3t,4t)[1]; A[0][1](-1)=> || (A(-1)=>)[0][1] -> -4 A(t)=<(t,2t:3t,4t)[1]; A[1][0](-1)=> || (A(-1)=>)[1][0] -> [MyErr]Invalid reference of array A(t)=<(t,2t:3t,4t)[0][0]; A[0][0](-1)=> || (A(-1)=>)[0][0] -> -1 A(t)=<(t,2t:3t,4t)[0][0]; A[0][1](-1)=> || (A(-1)=>)[0][1] -> [MyErr]Invalid reference of array ・Ver.2.79.31以降、反転参照可 A=<(1,2:3,4); A[-1][-1]=> -> 4 A=<(1,2:3,4); A[-2][-2]=> -> 1 A=<(1,2:3,4); A[-1][0]=> -> 3 A=<(1,2:3,4); A[-2][0]=> -> 1 A=<(1,2:3,4); A[-1][1]=> -> 4 A=<(1,2:3,4); A[-2][1]=> -> 2 A=<(1,2:3,4); A[0][-1]=> -> 2 A=<(1,2:3,4); A[0][-2]=> -> 1 A=<(1,2:3,4); A[1][-1]=> -> 4 A=<(1,2:3,4); A[1][-2]=> -> 3 ・未定義の行列要素の参照不可 A=<(1,2:3,4); A[-3][0]=> -> [MyErr]Invalid reference of array A=<(1,2:3,4); A[-3][1]=> -> [MyErr]Invalid reference of array A=<(1,2:3,4); A[0][-3]=> -> [MyErr]Invalid reference of array A=<(1,2:3,4); A[1][-3]=> -> [MyErr]Invalid reference of array A=<(1,2:3,4); A[0][2]=> -> [MyErr]Invalid reference of array A=<(1,2:3,4); A[2][0]=> -> [MyErr]Invalid reference of array A=<(1,2:3,4); A[0.1][0]=> -> [MyErr]Invalid reference of array A=<(1,2:3,4); A[0][0.2]=> -> [MyErr]Invalid reference of array |
|
目次
area参照 入力仕様 |
area参照の入力仕様と付随する留意事項について記述する
Ver.2.77.30以降、行列のarea参照とarea代入を追加 ・Ver.2.77.31以降、開始行/列indexが非整数の場合、予期せぬerror終了を修正 ・Ver.2.77.31以降、参照行/列sizeが非整数の場合、error終了に修正 ・Ver.2.78.31以降、反転機能の有効範囲を修正 ・Ver.2.79.32以降、参照行/列sizeが負の場合、予期せぬerror終了を修正 ・Ver.2.373.86以降、行列size指定のindexを厳格化 index:[0] ⇒ 空行列[]([0]指定の場合、初期化と異なり、size不正のerror終了) area参照 行列[開始行index][開始列index][参照行size][参照列size] 変数[開始行index][開始列index][参照行size][参照列size] 式変数[開始行index][開始列index][参照行size][参照列size]=> 式変数[開始行index][開始列index][参照行size][参照列size](arguments)=> ・矩形範囲の行列要素を参照する場合、4個の角括弧[]でindex/sizeを指定する A=(1,2:3,4:); A[0][0][][] || A[0][0][sizer(A)][sizec(A)] -> (1,2:3,4:0,0) ・参照行/列size=0の場合、参照size=行列size A=(1,2:3,4:); A[0][0][][1] || A[0][0][sizer(A)][1] -> (1:3:0) A=(1,2:3,4:); A[0][0][1][] || A[0][0][1][sizec(A)] -> (1,2) ・欠損要素を自動で埋める A=(1,2:3,4:); A -> (1,2:3,4:0) A=(1,2:3,4:); A[0][0][][] || trans(trans(A)) -> (1,2:3,4:0,0) ・参照行/列sizeを指定 A=(1,2:3,4:); A[0][0][1][1] || A[0][0] -> 1 A=(1,2:3,4:); A[1][0][1][1] || A[1][0] -> 3 A=(1,2:3,4:); A[0][1][1][1] || A[0][1] -> 2 A=(1,2:3,4:); A[0][0][2][2] -> (1,2:3,4) ・周期境界条件を適用 A=(1,2:3,4:); A[0][1][2][2] -> (2,1:4,3) A=(1,2:3,4:); A[1][1][2][2] -> (4,3:0,0) A=(1,2:3,4:); A[1][0][2][2] -> (3,4:0,0) A=(1,2:3,4:); A[2][0][2][2] -> (0,0:1,2) A=(1,2:3,4:); A[2][1][2][2] -> (0,0:2,1) A=(1,2:3,4:); A[1][0][][] -> (3,4:0,0:1,2) A=(1,2:3,4:); A[2][0][][] -> (0,0:1,2:3,4) A=(1,2:3,4:); A[0][1][][] -> (2,1:4,3:0,0) ・Ver.2.373.86以降、行列size指定のindex=0の場合、error終了 A=(1,2:3,4:); A[0][0][0][0] || A[0][0][0][] || A[0][0][][0] -> [MyErr]Invalid reference of array(area) ・未定義の行列要素の参照不可 A=(1,2:3,4:); A[3][0][][] -> [MyErr]Invalid reference of array(area) A=(1,2:3,4:); A[0][2][][] -> [MyErr]Invalid reference of array(area) A=(1,2:3,4:); A[0.1][0][][] -> [MyErr]Invalid reference of array(area) A=(1,2:3,4:); A[0][0.1][][] -> [MyErr]Invalid reference of array(area) A=(1,2:3,4:); A[0][0][0.1][0] -> [MyErr]Invalid reference of array(area) A=(1,2:3,4:); A[0][0][0][0.1] -> [MyErr]Invalid reference of array(area) A=(1,2:3,4:); A[0][0][-1][0] -> [MyErr]Invalid reference of array(area) A=(1,2:3,4:); A[0][0][0][-1] -> [MyErr]Invalid reference of array(area) ・開始行/列indexが負の場合、反転参照を定義する A=(1,2:3,4:); A[-1][-1][][] -> (0,0:4,3:2,1) A=(1,2:3,4:); A[-1][0][][] -> (0,0:3,4:1,2) A=(1,2:3,4:); A[-2][0][][] -> (3,4:1,2:0,0) A=(1,2:3,4:); A[-3][0][][] -> (1,2:0,0:3,4) A=(1,2:3,4:); A[-4][0][][] -> [MyErr]Invalid reference of array(area) A=(1,2:3,4:); A[0][-1][][] -> (2,1:4,3:0,0) A=(1,2:3,4:); A[0][-2][][] -> (1,2:3,4:0,0) A=(1,2:3,4:); A[0][-3][][] -> [MyErr]Invalid reference of array(area) |
|
目次
band参照 入力仕様 |
band参照の入力仕様と付随する留意事項について記述する
Ver.2.80.32以降、行列のband参照とband代入を追加 band参照 行列[帯index1][帯index2][帯index3]... 変数[帯index1][帯index2][帯index3]... 式変数[帯index1][帯index2][帯index3]...=> 式変数[帯index1][帯index2][帯index3]...(arguments)=> ・帯状範囲の行列要素を参照する場合、奇数個の角括弧[]で対角基準の相対indexを指定する 対角要素の場合、相対index=0 下三角行列範囲の場合、相対index<0 上三角行列範囲の場合、相対index>0 ・area代入を使用 A0=(1,2,3,4,5:6:7,,8,:9); A0 -> ( 1,2,3,4,5: 6: 7,0,8,0: 9 ) ・Ver.2.373.86以降、行列size指定のindexを厳格化([0] ⇒ 空行列[]) A=A0; A[0][0][][]=A; A -> ( 1,2,3,4,5: 6,0,0,0,0: 7,0,8,0,0: 9,0,0,0,0 ) ・欠損要素を自動で埋める A=A0; A[-1][0][1] -> ( 6,1,2: 0,0,0: 0,8,0: 0,0,0 ) ・帯状範囲の行列要素を列vectorに変換(上詰めで範囲外の行列要素=0) A=A0; A[-3][-2][-1][0][0][1][2][3][4] -> ( 9,7,6,1,1,2,3,4,5: 0,0,0,0,0,0,0,0,0: 0,0,0,8,8,0,0,0,0: 0,0,0,0,0,0,0,0,0 ) A=A0; A[-3][-3][-3] -> ( 9,9,9: 0,0,0: 0,0,0: 0,0,0 ) A=A0; A[-1][-1][-1] -> ( 6,6,6: 0,0,0: 0,0,0: 0,0,0 ) A=A0; A[0][0][0] -> ( 1,1,1: 0,0,0: 8,8,8: 0,0,0 ) A=A0; A[1][1][1] -> ( 2,2,2: 0,0,0: 0,0,0: 0,0,0 ) A=A0; A[3][3][3] -> ( 4,4,4: 0,0,0: 0,0,0: 0,0,0 ) ・対角要素の列vectorを列参照 A=A0; (A[-1][0][1])[e][1] -> A=A0; (A[0][0][0])[e][0] -> A=A0; A000=A[0][0][0]; A000[e][0] -> ( 1: 0: 8: 0 ) ・列vectorの行size A=A0; min(sizer(A),sizec(A)) -> 4 ・未定義の行列要素の参照不可 A=A0; A[-4][0][0] -> [MyErr]Invalid reference of array(band) A=A0; A[5][0][0] -> [MyErr]Invalid reference of array(band) A=A0; A[-0.3][0][0] -> [MyErr]Invalid reference of array(band) A=A0; A[0.3][0][0] -> [MyErr]Invalid reference of array(band) |
|
目次
行列への代入 入力仕様 |
行列への代入の入力仕様と付随する留意事項について記述する
行列への代入は変数を使用する ・よって変数への代入に同義として扱う 行列への参照は角括弧[]で指定する 行列への代入方法を列挙する ・行代入 ・列代入 ・要素代入 ・area代入 ・band代入 |
|
目次
行代入 入力仕様 |
行代入の入力仕様と付随する留意事項について記述する
Ver.2.78.31以降、行列の行参照と行代入の反転機能を追加 ・Ver.2.421.88以降、行列への代入の行列size比較を厳格化 A=(1,2:3,4); A[0]=A; A -> A=(1,2:3,4); A[0]=1 -> [MyErr]Invalid store size of array[0] 行代入 ・行vectorを代入する場合、1個の角括弧[]で行indexを指定する A=(,:,); A[0]=(1,2); A -> (1,2:0,0) A=(,:,); A[1]=(1,2); A -> (0,0:1,2) ・行参照を使用 A=(1,2:3,4); A[0]=A[1]; A -> (3,4:3,4) A=(1,2:3,4); A[1]=A[0]; A -> (1,2:1,2) ・欠損要素を自動で埋めない A=(,:); A[0]=(1,2); A -> (1,2:0) A=(:,); A[1]=(1,2); A -> (0:1,2) ・行indexが負の場合、反転代入を定義する A=(,:,); A[-1]=(1,2); A -> (0,0:1,2) A=(,:,); A[-2]=(1,2); A -> (1,2:0,0) ・未定義の行列要素への代入不可 A=(,:,); A[-3]=(1,2); A -> [MyErr]Invalid reference of array A=(,:,); A[2]=(1,2); A -> [MyErr]Invalid reference of array A=(,:,); A[0.3]=(1,2); A -> [MyErr]Invalid reference of array ・行列を代入した場合、最終行vectorを代入 A=(1,2:3,4); A[0]=A; A -> (3,4:3,4) A=(1,2:3,4); A[1]=A; A -> (1,2:3,4) A=(1,2:3,4); A[1]=trans(A); A -> (1,2:2,4) A=(1,2:3,4); A[1]=(A:A); A -> (1,2:3,4) ・列sizeの異なる代入不可 A=(1,2:3,4); A[1]=(A,A) -> [MyErr]Invalid store array A=(1,2:3,4); A[1]=1 -> [MyErr]Invalid store array A=(1,2:3,4); A[1]=(,,) -> [MyErr]Invalid store array A=(1,2:3,4); A[1]=(::) -> [MyErr]Invalid store array A=(1,2:3); A[1]=0 -> (1,2:0) ・式変数への代入不可 clear; A=<(1,2:3,4); A[1]=(,) -> [MyErr]Invalid SEv-scope(A) clear; A=<(1,2:3,4); (A=>)[1]=(,) || =(,)-(A=>)[1] -> (-3,-4) test caseを列挙する A=(1,2:3,4); A[1]=A[0]; A -> (1,2:1,2) A=(1,2:3,4); A[1]=-A[1]; A -> (1,2:-3,-4) A=(1,2:3,4); A[1]=-2A[1]; A -> (1,2:-6,-8) A=(1,2:3,4); A[1]=(,); A -> (1,2:0,0) A=(1,2:3,4); w=A[1]; A[1]=A[0]; A[0]=w; A -> (3,4:1,2) A=(1,2:); A[0]=A[1] -> [MyErr]Invalid store array A=(1,2:); A[1]=A[0] -> [MyErr]Invalid store array A=(1,2:); ttA=trans(trans(A)); ttA[0]=ttA[1]; ttA -> (0,0:0,0) A=(1,2:); ttA=trans(trans(A)); ttA[1]=ttA[0]; ttA -> (1,2:1,2) A=(1,2:,); A[0]=A[1]; A -> (0,0:0,0) A=(1,2:,); A[1]=A[0]; A -> (1,2:1,2) A=(1,2:3,4); A[0]=A; A -> (3,4:3,4) A=(1,2:3,4); A[0]=(A:A(2,:,2)); A -> (6,8:3,4) |
|
目次
列代入 入力仕様 |
列代入の入力仕様と付随する留意事項について記述する
Ver.2.76.29以降、行列の列参照と列代入を追加 ・Ver.2.78.31以降、行列の列参照と列代入の反転機能を追加 ・Ver.2.78.31以降、error判定処理を分割 ・Ver.2.79.31以降、行index=-1 ⇒ Napier数eに演算仕様変更 ・Ver.2.170.41以降、列代入の[e]を空行列で代替可 Ver.2.747.112以降、列参照と列代入の[e]を廃止 ・Ver.2.421.88以降、行列への代入の行列size比較を厳格化 A=(1,2:3,4); A[][0]=A; A -> A=(1,2:3,4); A[][0]=1 -> [MyErr]Invalid store size of array[][0] 列代入 ・列vectorを代入する場合、2個の角括弧[]で行indexにNapier数e||空行列を指定する A=(,:,); A[][0]={1,2}; A -> (1,0:2,0) A=(,:,); A[e][0]={1,2}; A -> (1,0:2,0) A=(,:,); A[e][1]={1,2}; A -> (0,1:0,2) ・列参照を使用 A=(1,2:3,4); A[e][1]=A[e][0]; A -> (1,1:3,3) A=(1,2:3,4); A[e][1]=A[e][1]; A -> (1,2:3,4) A=(1,2:3,4); A[e][0]=A[e][1]; A -> (2,2:4,4) ・欠損要素を自動で埋める A=(:,); A[e][1]={1,2}; A -> (0,1:0,2) A=(:,:); A[e][1]={1,2,3}; A -> (0,1:0,2:0,3) A=(:,:); A[e][0]={1,2,3}; A -> (1,0:2,0:3,0) ・同義 set_vectorc(A,ic,vc)=<[tA=trans(A),tA[ic]=trans(vc),=<trans(tA)]=>; A=(:,:); A=set_vectorc(=<A,0,=<{1,2,3}); A -> (1,0:2,0:3,0) A=(:,:); A=set_vectorc(=<A,1,=<{1,2,3}); A -> (0,1:0,2:0,3) ・未定義の行列要素への代入不可 A=(:,:); A=set_vectorc(=<A,2,=<{1,2,3}); A -> [MyErr]Invalid reference of array A=(:,:); A[e][2]={1,2,3}; A -> [MyErr]Invalid reference of array(column) A=(:,:); A[e][0.3]={1,2,3}; A -> [MyErr]Invalid reference of array(column) ・行列を代入した場合、最終列vectorを代入 A=(1,2:3,4); A[e][0]=A; A -> (2,2:4,4) A=(1,2:3,4); A[e][0]=(A,A(2,:,2)); A -> (4,2:8,4) ・行sizeの異なる代入不可 A=(,:,); A[e][0]=(A:A) -> [MyErr]Invalid store array(column) A=(,:,); A[e][0]=(1) -> [MyErr]Invalid store array(column) A=(,:,); A[e][0]=(1,2) -> [MyErr]Invalid store array(column) A=(,:,); A[e][0]={1,2,3} -> [MyErr]Invalid store array(column) ・列indexが負の場合、反転代入を定義する A=(1,2:3,4); A[e][-1]=A[e][0]; A -> (1,1:3,3) A=(1,2:3,4); A[e][-1]=A[e][1]; A -> (1,2:3,4) A=(1,2:3,4); A[e][-2]=A[e][1]; A -> (2,2:4,4) A=(1,2:3,4); A[e][-3]=A[e][1]; A -> [MyErr]Invalid reference of array(column) ・転置行列関数を使用 A=(1,2:3,4); tA=trans(A); tA[0]=-tA[0]; A=trans(tA); A -> (-1,2:-3,4) |
|
目次
要素代入 入力仕様 |
要素代入の入力仕様と付随する留意事項について記述する
要素代入 ・行列要素を代入する場合、2個の角括弧[]で行/列indexを指定する A=(,:); A[0][0]=1; A -> (1,0:0) ・欠損要素を自動で埋めない A=(,:); A[0][1]=1; A -> (0,1:0) A=(,:); A[1][0]=1; A -> (0,0:1) A=(,:); A[1][1]=1; A -> [MyErr]Invalid reference of array ・行列を代入した場合、最終要素を代入 ・Ver.2.421.88以降、行列への代入の行列size比較を厳格化 A=(1,2:3,4); A[0][0]=A; A -> A=(1,2:3,4); A[0][0]=first(A); A -> (1,2:3,4) A=(1,2:3,4); A[1][1]=(x=2,-2x); A -> (1,2:3,-4) ・Ver.2.79.31以降、反転代入可 A=(1,2:3,4); A[-1][-1]=-1; A -> (1,2:3,-1) A=(1,2:3,4); A[-2][-2]=-1; A -> (-1,2:3,4) A=(1,2:3,4); A[-1][0]=-1; A -> (1,2:-1,4) A=(1,2:3,4); A[-2][0]=-1; A -> (-1,2:3,4) A=(1,2:3,4); A[-1][1]=-1; A -> (1,2:3,-1) A=(1,2:3,4); A[-2][1]=-1; A -> (1,-1:3,4) A=(1,2:3,4); A[0][-1]=-1; A -> (1,-1:3,4) A=(1,2:3,4); A[0][-2]=-1; A -> (-1,2:3,4) A=(1,2:3,4); A[1][-1]=-1; A -> (1,2:3,-1) A=(1,2:3,4); A[1][-2]=-1; A -> (1,2:-1,4) ・未定義の行列要素への代入不可 A=(1,2:3,4); A[-3][0]=-1 -> [MyErr]Invalid reference of array A=(1,2:3,4); A[-3][1]=-1 -> [MyErr]Invalid reference of array A=(1,2:3,4); A[0][-3]=-1 -> [MyErr]Invalid reference of array A=(1,2:3,4); A[1][-3]=-1 -> [MyErr]Invalid reference of array A=(1,2:3,4); A[0][2]=-1 -> [MyErr]Invalid reference of array A=(1,2:3,4); A[2][0]=-1 -> [MyErr]Invalid reference of array A=(1,2:3,4); A[0.1][0]=-1 -> [MyErr]Invalid reference of array A=(1,2:3,4); A[0][0.2]=-1 -> [MyErr]Invalid reference of array ・式変数への代入不可 clear; A=<(1,2:3,4); A[1][1]=0 -> [MyErr]Invalid SEv-scope(A) clear; A=<(1,2:3,4); (A=>)[1][1]=0 || =0-4 -> -4 test caseを列挙する A=(1,2:3,4); A[0][0]=-1; A -> (-1,2:3,4) A=(1,2:3,4); ii=1; A[ii][ii]=-1; A -> (1,2:3,-1) A=(1,2:3,4); A[1][1]=(x=2); A -> (1,2:3,0) |
|
目次
area代入 入力仕様 |
area代入の入力仕様と付随する留意事項について記述する
Ver.2.77.30以降、行列のarea参照とarea代入を追加 ・Ver.2.77.31以降、開始行/列indexが非整数の場合、予期せぬerror終了を修正 ・Ver.2.78.31以降、反転機能の有効範囲を修正 ・Ver.2.78.31以降、error判定処理を分割 ・Ver.2.79.32以降、参照行/列sizeが負の場合、error判定処理を修正 ・Ver.2.373.86以降、行列size指定のindexを厳格化 index:[0] ⇒ 空行列[]([0]指定の場合、初期化と異なり、size不正のerror終了) area代入 ・矩形範囲の行列要素を代入する場合、4個の角括弧[]でindex/sizeを指定する A=(1,2:3,4:); A[0][0][][]=A; A -> (1,2:3,4:0,0) A=(1,2:3,4:); A[0][0][sizer(A)][sizec(A)]=A; A -> (1,2:3,4:0,0) ・欠損要素を自動で埋める A=(1,2:3,4:); A=A; A -> (1,2:3,4:0) A=(1,2:3,4:); ttA=trans(trans(A)); ttA -> (1,2:3,4:0,0) ・周期境界条件を適用 A=(1,2:3,4:); A[1][0][][]=A; A -> (0,0:1,2:3,4) A=(1,2:3,4:); A[2][0][][]=A; A -> (3,4:0,0:1,2) A=(1,2:3,4:); A[0][1][][]=A; A -> (2,1:4,3:0,0) A=(1,2:3,4:); A[0][0][2][2]=A[1][1][2][2]; A -> (4,3:0,0:0,0) A=(1,2:3,4:); A[1][1][2][2]=A[0][0][2][2]; A -> (1,2:2,1:4,3) ・Ver.2.373.86以降、行列size指定のindex=0の場合、error終了 A=(1,2:3,4:); A[0][0][0][0]=1 || A[0][0][0][]=1 || A[0][0][][0]=1 -> [MyErr]Invalid reference of array(area) ・未定義の行列要素への代入不可 A=(1,2:3,4:); A[3][0][][]=A; A -> [MyErr]Invalid reference of array(area) A=(1,2:3,4:); A[0][2][][]=A; A -> [MyErr]Invalid reference of array(area) A=(1,2:3,4:); A[0.1][0][][]=A; A -> [MyErr]Invalid reference of array(area) A=(1,2:3,4:); A[0][0.1][][]=A; A -> [MyErr]Invalid reference of array(area) A=(1,2:3,4:); A[0][0][0.1][]=A; A -> [MyErr]Invalid reference of array(area) A=(1,2:3,4:); A[0][0][][0.1]=A; A -> [MyErr]Invalid reference of array(area) A=(1,2:3,4:); A[0][0][5][5]=A; A -> [MyErr]Invalid reference of array(area) A=(1,2:3,4:); A[0][0][2][2]=A; A -> [MyErr]Invalid store array(area) A=(1,2:3,4:); A[0][0][-1][]=A; A -> [MyErr]Invalid reference of array(area) A=(1,2:3,4:); A[0][0][][-1]=A; A -> [MyErr]Invalid reference of array(area) ・開始行/列indexが負の場合、反転代入を定義する A=(1,2:3,4:); A[-1][-1][][]=A; A -> (0,0:4,3:2,1) ・上下反転 A=(1,2:3,4:); A[-1][0][][]=A; A -> (0,0:3,4:1,2) A=(1,2:3,4:); A[-2][0][][]=A; A -> (3,4:1,2:0,0) A=(1,2:3,4:); A[-3][0][][]=A; A -> (1,2:0,0:3,4) A=(1,2:3,4:); A[-4][0][][]=A; A -> [MyErr]Invalid reference of array(area) ・左右反転 A=(1,2:3,4:); A[0][-1][][]=A; A -> (2,1:4,3:0,0) A=(1,2:3,4:); A[0][-2][][]=A; A -> (1,2:3,4:0,0) A=(1,2:3,4:); A[0][-3][][]=A; A -> [MyErr]Invalid reference of array(area) ・Ver.2.373.86以降、行列size指定のindexを厳格化([0] ⇒ 空行列[]) A=(1,2:3,4:); A[-1][-1][][]=A[-1][-1][0][0]; A -> A=(1,2:3,4:); A[-1][-1][][]=A[-1][-1][][]; A -> (1,2:3,4:0,0) A=(1,2:3,4:); A[-1][-1][2][2]=A[-1][-1][2][2]; A -> (1,2:3,4:0,0) A=(1,2:3,4:); A[-1][-1][2][2]=A[0][0][2][2]; A -> (1,2:4,3:2,1) A=(1,2:3,4:); A[-1][-1][2][2]=A[1][1][2][2]; A -> (1,2:0,0:3,4) |
|
目次
band代入 入力仕様 |
band代入の入力仕様と付随する留意事項について記述する
Ver.2.80.32以降、行列のband参照とband代入を追加 band代入 ・帯状範囲の行列要素を代入する場合、奇数個の角括弧[]で対角基準の相対indexを指定する A0=zeros(4,4); A0=(A0,0); A0 -> ( 0,0,0,0,0: 0,0,0,0: 0,0,0,0: 0,0,0,0 ) ・欠損要素を自動で埋める A=A0; A[-1][0][1]=(1,2,3); A -> ( 2,3,0,0,0: 1,2,3,0,0: 0,1,2,3,0: 0,0,1,2,3 ) A=A0; A[-1][0][1]=(1,2,3); A[-1][0][1]=A[-1][0][1]; A -> ( 2,3,0,0,0: 1,2,3,0,0: 0,1,2,3,0: 0,0,1,2,3 ) ・相対index固定の場合、後要素で上書き A=A0; A[0][0][0]=(1,2,3); A -> ( 3,0,0,0,0: 0,3,0,0,0: 0,0,3,0,0: 0,0,0,3,0 ) ・band参照で相対indexを交換する場合、意図とは異なる可能性あり A=A0; A[-1][0][1]=(1,2,3); A[-1][0][1]=A[1][0][-1]; A -> A=A0; A[-1][0][1]=(1,2,3); A[1][0][-1]=A[-1][0][1]; A -> ( 2,1,0,0,0: 3,2,1,0,0: 0,3,2,1,0: 0,0,3,2,0 ) ・3重帯行列 A=A0; A[-2][0][2]=(1,2,3); A -> ( 2,0,3,0,0: 0,2,0,3,0: 1,0,2,0,3: 0,1,0,2,0 ) A=A0; A[-3][0][3]=(1,2,3); A -> ( 2,0,0,3,0: 0,2,0,0,3: 0,0,2,0,0: 1,0,0,2,0 ) A=A0; A[-3][0][4]=(1,2,3); A -> ( 2,0,0,0,3: 0,2,0,0,0: 0,0,2,0,0: 1,0,0,2,0 ) ・複数行の代入 A=A0; A[-1][0][1]=(1,2,3:4,5,6); A -> ( 2,3,0,0,0: 1,5,6,0,0: 0,4,5,6,0: 0,0,4,5,6 ) A=A0; A[-1][0][1]=(1,2,3:4,5,6:7,8,9); A -> ( 2,3,0,0,0: 1,5,6,0,0: 0,4,8,9,0: 0,0,7,8,9 ) A=A0; A[-1][0][1]=(1,2,3:4,5,6:7,8,9:10,11,12); A -> ( 2,3,0,0,0: 1,5,6,0,0: 0,4,8,9,0: 0,0,7,11,12 ) A=A0; A[-1][0][1]=(1,2,3:4,5,6:7,8,9:10,11,12:13,14,15); A -> ( 2,3,0,0,0: 1,5,6,0,0: 0,4,8,9,0: 0,0,7,11,12 ) A=A0; A[-2][0][2]=(1,2,3:4,5,6:7,8,9:10,11,12:13,14,15); A -> ( 2,0,3,0,0: 0,5,0,6,0: 1,0,8,0,9: 0,4,0,11,0 ) A=A0; A[-3][0][3]=(1,2,3:4,5,6:7,8,9:10,11,12:13,14,15); A -> ( 2,0,0,3,0: 0,5,0,0,6: 0,0,8,0,0: 1,0,0,11,0 ) A=A0; A[-3][0][4]=(1,2,3:4,5,6:7,8,9:10,11,12:13,14,15); A -> ( 2,0,0,0,3: 0,5,0,0,0: 0,0,8,0,0: 1,0,0,11,0 ) ・5重帯行列 A=A0; A[-2][-1][0][1][2]=(1,2,3,4,5); A -> ( 3,4,5,0,0: 2,3,4,5,0: 1,2,3,4,5: 0,1,2,3,4 ) ・任意行列 A=A0; A[-2][-1][0][1][2]=(1,2,3,4,5:6,7,8,9,10:); A -> ( 3,4,5,0,0: 2,8,9,10,0: 1,7,0,0,0: 0,6,0,0,0 ) ・未定義の行列要素への代入不可 A=A0; A[-4][0][0]=(1,2,3) -> [MyErr]Invalid reference of array(band) A=A0; A[0][0][5]=(1,2,3) -> [MyErr]Invalid reference of array(band) A=A0; A[0.3][0][0]=(1,2,3) -> [MyErr]Invalid reference of array(band) ・列sizeの異なる代入不可 A=A0; A[0][0][0]=1 -> [MyErr]Invalid store array(band) A=A0; A[0][0][0]=(1,2) -> [MyErr]Invalid store array(band) |
|
目次
行列結合 入力仕様 |
行列結合の入力仕様と付随する留意事項について記述する
vectorの結合 ((1,2),(3,4)) -> (1,2,3,4) x=(1,2); y=(3,4); (x,y) -> (1,2,3,4) A=(1,2:3,4); (A[0],A[1]) -> (1,2,3,4) (vector4c,vector4c,vector4c) -> (0,0,0:0,0,0:0,0,0:0,0,0) ・区切り文字の左から順に結合する ((1,2),{3,4},{3,4,5}) -> (1,2,3,3:0,0,4,4:0,0,0,5) ((1,2:),{3,4},{3,4,5}) -> (1,2,3,3:0,0,4,4:0,0,0,5) ((1,2:,),{3,4},{3,4,5}) -> (1,2,3,3:0,0,4,4:0,0,0,5) ((1,2:,:,),{3,4},{3,4,5}) -> (1,2,3,3:0,0,4,4:0,0,0,5) ((1,2:,:,),{3,4,},{3,4,5}) -> (1,2,3,3:0,0,4,4:0,0,0,5) 行列の結合 ((1,2:5,6),(3,4:7,8):{-1,-5:-2,-6},{-3,-7:-4,-8}) -> (1,2,3,4:5,6,7,8:-1,-2,-3,-4:-5,-6,-7,-8) (zeros2,zeros2:zeros2,zeros2) -> (0,0,0,0:0,0,0,0:0,0,0,0:0,0,0,0) ・変数を使用 mat00=(1,2:5,6); mat01=(3,4:7,8); mat10={-1,-5:-2,-6}; mat11={-3,-7:-4,-8}; mat=(mat00,mat01:mat10,mat11); mat -> (1,2,3,4:5,6,7,8:-1,-2,-3,-4:-5,-6,-7,-8) |
|
目次
irregular 行列 入力仕様 |
irregular行列の入力仕様と付随する留意事項について記述する
・Ver.2.156.38以降、行列結合で欠損要素を埋めない(挙動を明確化) 列指定のirregular行列 {1:2:3,4} -> (1,2,3: {1:2,3} -> (1,2: {1:2,,3} -> (1,2: {1,2:3,,,4} -> (1,3:2,0: {1,,,2:3,4:5,,,,,6} -> (1,3,5:0,4,0:0, 行指定のirregular行列 A=(11:21,22:31,32,33,34); A -> (11:21,22:31,32,33,34) tA={11:21,22:31,32,33,34}; tA -> (11,21,31: ・行指定の行列で欠損要素がある場合、転置行列関数を使用 A=(11:21,22:31,32,33,34); trans(trans(A)) -> (11,0,0,0:21,22,0,0:31,32,33,34) A=(11:21,22:31,32,33,34); htrans(htrans(A)) -> (11,0,0,0:21,22,0,0:31,32,33,34) ・単位tree構造の仕様上、行vectorの欠損要素を自動で埋めない (1,2:3),(1,2:3) -> ( 1,2,1,2: 3,3 ) (1:3,4),(1:3,4) -> ( 1,1: 3,4,3,4 ) {1,2:3},{1,2:3} -> ( 1,3,1,3: 2,2 ) {1:3,4},{1:3,4} -> ( 1,3,1,3: ) 多重列挙の結合 {(1,2),(3:4)} -> (1,2:3:4) {(1,2):(3:4)} -> (1,2,3: (1,{2,3}) -> (1,2: (1,(2:3),4) -> (1,2,4: (1,{2,(3,{4,5})}) -> (1,2: (1,{2:3},4) -> (1,2,3,4) {1,{2:3},4} -> (1:2,3:4) {1,(2:3),4} -> (1:2:3:4) irregular行列の結合 {1,2:3},{1,2:3} -> (1,3,1,3:2,2) (1,2),{3,4:5:6,7:8} -> (1,2,3,5,6,8: (1,2),{3,4:5:6,7:8,9,10} -> (1,2,3,5,6,8: (1,2),{3,4:5:6,7:8,(9,10)} -> (1,2,3,5,6,8: (1,(2,3):({4,5}),6,{7,8,(9,10)}) -> ( 1,2,3: 4,6,7: 5, ) {1,(2,3,4),2:{3,4,5}:{6,,,,,7}} -> ( 1,3,6: 2,3,4,4,0: 2,5,0: ) A=(1,{2,3,4,5},(6,7,{8,9}):({10,11}),12,{13,14,(15,16,{17,18})}); A -> ( 1,2,6,7,8: 10,12,13: 11, ) ttA=trans(trans(A)); ttA -> ( 1,2,6,7,8: 10,12,13,0,0: 11, ) A-ttA -> ( 0,0,0,0,0: 0,0,0,0,0: 0,0,0,0,0: 0,0,0,0,0: 0,0,0,0,0: 0,0,0,0,0: 0,0,0,0,0: 0,0,0,0,0 ) |
|
目次
特殊仕様 行列関数 入力仕様 |
特殊仕様行列関数の入力仕様と付随する留意事項について記述する
回転行列 ・右手系の直交座標系の各軸周りの回転行列を演算して返す ・返値の回転行列は引数の誤差情報を継承しない rotationx(第1引数) rotationy(第1引数) rotationz(第1引数) ・第1引数: Euler角の弧度数実数値radを値渡し test caseを列挙する (sqrt2,,:,sqrt2,:,,sqrt2)rotationx(pi/4) -> (1.4142135623730951,0,0: 0,1.0000000000000002,-1: 0,1,1.0000000000000002) (sqrt2,,:,sqrt2,:,,sqrt2)rotationx(-pi/4) -> (1.4142135623730951,0,0: 0,1.0000000000000002,1: 0,-1,1.0000000000000002) (sqrt2,,:,sqrt2,:,,sqrt2)rotationy(pi/4) -> (1.0000000000000002,0,1: 0,1.4142135623730951,0: -1,0,1.0000000000000002) (sqrt2,,:,sqrt2,:,,sqrt2)rotationy(-pi/4) -> (1.0000000000000002,0,-1: 0,1.4142135623730951,0: 1,0,1.0000000000000002) (sqrt2,,:,sqrt2,:,,sqrt2)rotationz(pi/4) -> (1.0000000000000002,-1,0: 1,1.0000000000000002,0: 0,0,1.4142135623730951) (sqrt2,,:,sqrt2,:,,sqrt2)rotationz(-pi/4) -> (1.0000000000000002,1,0: -1,1.0000000000000002,0: 0,0,1.4142135623730951) t=_dx(=<{x},1,1)pi/4+1000i; t -> infoLost[ i] 0.7853981633974194+1000i+O(8e-13+8e-13i) (sqrt2,,:,sqrt2,:,,sqrt2)rotationx(t) -> (1.4142135623730951,0,0: 0,1.0000000000000289,-0.9999999999999711: 0,0.9999999999999711,1.0000000000000289) 回転行列の引数の誤差情報を継承する場合 t=_dx(=<{x},1,1)pi/4+1000i; rt=real(t); rt -> infoLost[ i] 0.7853981633974194+O(8e-13) rotx=<(1,0,0:0,cos(rt),-sin(rt):0,sin(rt),cos(rt)); rotx -> (1,0,0: 0,infoLost[ i] 0.7071067811865679+O(6e-13), infoLost[ i] -0.707106781186527+O(6e-13): 0,infoLost[ i] 0.707106781186527+O(6e-13), infoLost[ i] 0.7071067811865679+O(6e-13)) ・一続きにまとめる場合 t=_dx(=<{x},1,1)pi/4+1000i; rotx=<{rt=real(t),=<(1,0,0:0,cos(rt),-sin(rt):0,sin(rt),cos(rt))}=>; (sqrt2,,:,sqrt2,:,,sqrt2)rotx -> (1.4142135623730951,infoLost[ i] 0,infoLost[ i] 0: 0,infoLost[ i] 1.0000000000000289+O(8e-13), infoLost[ i] -0.9999999999999711+O(8e-13): 0,infoLost[ i] 0.9999999999999711+O(8e-13), infoLost[ i] 1.0000000000000289+O(8e-13)) 回転行列を式変数で定義する場合 ・各軸x/y/zに対するEuler角をphi/theta/psiとする rotx=<{rt=real(phi),=<(1,,:,cos(rt),-sin(rt):,sin(rt),cos(rt))}=>; roty=<{rt=real(theta),=<(cos(rt),,sin(rt):,1,:-sin(rt),,cos(rt))}=>; rotz=<{rt=real(psi),=<(cos(rt),-sin(rt),:sin(rt),cos(rt),:,,1)}=>; phi=pi/5; rotx-rotationx(phi) -> (0,0,0:0,0,0:0,0,0) theta=pi/5; roty-rotationy(theta) -> (0,0,0:0,0,0:0,0,0) psi=pi/5; rotz-rotationz(psi) -> (0,0,0:0,0,0:0,0,0) 回転行列の一般化 ・関数を使用する場合 rotx=<{rotationx(phi)}; roty=<{rotationy(theta)}; rotz=<{rotationz(psi)}; ・式変数で定義する場合 rotx=<{rt=real(phi),=<(1,,:,cos(rt),-sin(rt):,sin(rt),cos(rt))}=>; roty=<{rt=real(theta),=<(cos(rt),,sin(rt):,1,:-sin(rt),,cos(rt))}=>; rotz=<{rt=real(psi),=<(cos(rt),-sin(rt),:sin(rt),cos(rt),:,,1)}=>; ・一般化した回転行列rot_は対象行列mat||列vectorの左から演算する mat_after=rot_*mat_before {$x_after,$y_after,$z_after}=rot_*{x_before,y_before,z_before} ・よって回転順序は回転行列並び順の逆順となる ・回転順序x⇒y⇒z rot_zyx=<{rotz*roty*rotx}; phi=pi/4; theta=3pi/4; psi=-3pi/4; ans_zyx=rot_zyx; ans_zyx -> (0.4999999999999999,0.14644660940672638,-0.8535533905932737: 0.5,-0.8535533905932737,0.14644660940672605: -0.7071067811865476,-0.4999999999999999,-0.5) ・回転順序z⇒y⇒x rot_xyz=<{rotx*roty*rotz}; phi=-pi/4; theta=-3pi/4; psi=3pi/4; ans_xyz=rot_xyz; ans_xyz -> (0.4999999999999999,0.5,-0.7071067811865476: 0.14644660940672638,-0.8535533905932737,-0.4999999999999999: -0.8535533905932737,0.14644660940672605,-0.5) ・回転の逆回転を順序通りに記憶して演算すると単位行列に戻る rot_xyz*rot_zyx // NG -> ... ans_xyz*ans_zyx -> (1,5.551115123125783e-17,5.551115123125783e-17: 5.551115123125783e-17,0.9999999999999999,0: 5.551115123125783e-17,0,0.9999999999999999) ans_zyx*ans_xyz -> (0.9999999999999999,0,-5.551115123125783e-17: 0,0.9999999999999999,-5.551115123125783e-17: -5.551115123125783e-17,-5.551115123125783e-17,1) ・回転順序y⇒x⇒z rot_zxy=<{rotz*rotx*roty}; phi=pi/4; theta=3pi/4; psi=-3pi/4; ans_zxy=rot_zxy; ans_zxy -> (0.8535533905932737,0.5000000000000001,-0.14644660940672627: 0.14644660940672627,-0.5,-0.8535533905932737: -0.5000000000000001,0.7071067811865475,-0.5) ・回転順序z⇒x⇒y rot_yxz=<{roty*rotx*rotz}; phi=-pi/4; theta=-3pi/4; psi=3pi/4; ans_yxz=rot_yxz; ans_yxz -> (0.8535533905932737,0.14644660940672627,-0.5000000000000001: 0.5000000000000001,-0.5,0.7071067811865475: -0.14644660940672627,-0.8535533905932737,-0.5) ・同じく回転の逆回転を順序通りに記憶して演算すると単位行列に戻る ans_yxz*ans_zxy -> (1,5.551115123125783e-17,0:5.551115123125783e-17,1,0:0,0,1) ans_zxy*ans_yxz -> (1,0,-5.551115123125783e-17:0,1,0:-5.551115123125783e-17,0,1) 3D-graphicsで主流の左手系 rotx_LHS=<{rt=real(phi),=<(1,,:,cos(rt),sin(rt):,-sin(rt),cos(rt))}=>; roty_LHS=<{rt=real(theta),=<(cos(rt),,-sin(rt):,1,:sin(rt),,cos(rt))}=>; rotz_LHS=<{rt=real(psi),=<(cos(rt),sin(rt),:-sin(rt),cos(rt),:,,1)}=>; ・同義 rotx_LHS=<{w=phi,phi=-phi,ret=rotx,phi=w,=<ret}=>; roty_LHS=<{w=theta,theta=-theta,ret=roty,theta=w,=<ret}=>; rotz_LHS=<{w=psi,psi=-psi,ret=rotz,psi=w,=<ret}=>; ・test caseを示す phi=pi/4; rotx -> ( 1,0,0: 0,0.7071067811865476,-0.7071067811865475: 0,0.7071067811865475,0.7071067811865476 ) rotx_LHS -> ( 1,0,0: 0,0.7071067811865476,0.7071067811865475: 0,-0.7071067811865475,0.7071067811865476 ) |
|
目次
変数 入力仕様 |
変数の入力仕様と付随する留意事項について記述する
変数への代入・再代入方法は、変数名=代入値とする x=2; x -> 2 ・漸化式を記述するため、再代入を許容する x=2; x=4; x -> 4 x=2; x=2x; x -> 4 ・Ver.2.249.57以降、再代入と重複宣言を禁止するconst宣言を暫定追加($開始のbeta版) |
|
目次
変数への 代入規則 |
変数への代入規則と付随する留意事項について記述する
変数への代入規則を列挙する ・代入する変数の左側に数値や演算子を置けない clear; 2x=3 -> [MyErr]Invalid ans isFound clear; 3+x=4 -> [MyErr]Invalid binary operation ・値のみ代入可 clear; x=1; x -> 1 clear; x=(1,2); x -> (1,2) clear; a=1; b=2; c=a+b; c -> 3 ・複数の変数に多重代入不可 clear; a=b=1 -> [MyErr]Invalid ans isFound ・未定義変数の代入不可 clear; a=1; c=a+b; c -> [MyErr]Invalid binary operation clear; x=y(z) -> [MyErr]Invalid ans isFound ・未定義変数を含む場合、式変数を使用 |
|
目次
変数の 命名規則 |
変数の命名規則と付随する留意事項について記述する
変数の命名規則を列挙する ・大文字と小文字を区別する x=1; X=2; x+X -> 3 ・変数名の後に続く数字は変数名に含まれる x0=1; x1=2; x0+x1 -> 3 ・特殊仕様関数は関数名の後に続く数字が引数に含まれる sort000(1) -> 1 sort000=1 -> [MyErr]Invalid ans isFound sort0x33=1; sort0x33 -> 1 ・ASCII文字(code-point<128)の全角は半角に変換される Ver.2.869.162以降、訂正 X=3;X -> 3 ・Multi-Byte文字を使用可 番号=1; 番号 -> 1 ・予約語は使用不可 max=3 -> [MyErr]Invalid ans isFound ・Ver.2.27.15以降、$から開始不可 ・Ver.2.249.57以降、再代入と重複宣言を禁止するconst宣言を暫定追加($開始のbeta版) $a=1; a -> 1 $$a=1 -> [MyErr]Invalid symbol ・数字から開始不可 clear; 2x=4 -> [MyErr]Invalid ans isFound ・single||double quotation mark使用不可 "x"=2; "x" || x -> 2 ""=2 || =2 -> 2 ・Ver.2.165.39以降、reserved token記号の単体使用不可 . -> [MyErr]reserved token(.) ' -> [MyErr]reserved token(') " -> [MyErr]reserved token(") "x" -> [MyErr]reserved token(") |
|
目次
escape記号 入力仕様 |
escape記号と付随する留意事項について記述する
Ver.2.301.72以降、$記号を予約語に追加(変数名symbolに使用不可) ・Ver.2.232.56以降、symbol表記に統一 ・Ver.2.246.57以降、name渡しに対応 ・Ver.2.248.57以降、$$開始の場合、parse段階でerror終了 ・Ver.2.248.57以降、dummy ⇒ symbol ・Ver.2.249.57以降、再代入と重複宣言を禁止するconst宣言を暫定追加($開始のbeta版) test caseを列挙する $ -> [MyErr]Invalid null string($) $x -> [MyErr]Invalid REv($x) $$x || $$$x -> [MyErr]Invalid symbol $max || $$max || $$$max -> [MyErr]Invalid symbol ・Ver.2.30.16以降、予約語への代入不可 clear; ($max)=(2) -> [MyErr]Invalid symbol clear; $0xf -> [MyErr]Invalid symbol clear; ($0xf)=1 -> [MyErr]Invalid symbol ・行列要素pattern matching ($$a)=1 -> [MyErr]Invalid symbol ($$$a)=1 -> [MyErr]Invalid symbol ・高階関数 _s$n(=<{0},1,2) -> [MyErr]Invalid ans isFound _s$$n(=<{0},1,2) -> [MyErr]Invalid ans isFound ・高階行列関数 _ex(=<{$$x},2,2) -> [MyErr]Invalid symbol _e$x(=<{x},2,2) -> [MyErr]Invalid ans isFound _e$$x(=<{x},2,2) -> [MyErr]Invalid symbol |
|
目次
変数名 symbol 入力仕様 |
変数名symbolの入力仕様と付随する留意事項について記述する
変数名symbolと表記するcaseを列挙する ・plot2d-commandの引数に変数名を渡す場合 ・最上位関数の引数に変数名を渡す場合 ・高階関数の引数に変数名を式渡しで渡す場合 ・高階行列関数の引数に変数名を式渡しで渡す場合 ・symbolic高階行列関数の代入する式変数に変数名を渡す場合 変数名symbolの式渡しが不要なcaseを列挙する ・括弧より関数優先の場合 変数名symbolの式渡し(高階関数の引数)について ・単体で渡す場合、最終要素のsymbol名を参照 ・列vectorで渡す場合、各行vectorの最終要素のsymbol名を参照 Ver.2.32.17以降、すべての変数名symbolは変数の命名規則に準拠 ・Ver.2.232.56以降、symbol表記に統一 ・Ver.2.246.57以降、name渡しに対応 ・Ver.2.248.57以降、$$開始の場合、parse段階でerror終了 ・Ver.2.248.57以降、dummy ⇒ symbol ・Ver.2.249.57以降、再代入と重複宣言を禁止するconst宣言を暫定追加($開始のbeta版) delVar($x) -> f(=<$x)=<x; f(=<x) -> [MyErr]Invalid f(=<x)=<x; f(=<$x) -> [MyErr]Invalid symbol($x) Jacobi(=<{2x^2},=<{$x},=<{1}) -> |
|
目次
予約変数 入力仕様 |
予約変数の入力仕様と付随する留意事項について記述する
予約変数ans ・直前の実行文の演算結果を保持する 2; ans*2; ans*2; ans -> 8 2; (ans*2,ans*3); ans -> (4,6) ・変数への代入||式変数への式代入の場合、ansは更新されない 2; x=3; ans -> 2 2; x=<3; ans -> 2 ・error終了の場合、ansは更新されない 予約変数__n__ Ver.2.381.86以降、追加 ・再帰高階関数の繰り返し回数=1~のdummy変数を一時的に保持する clear; _r(=<arr.push(__n__),arr=[],10); arr -> (1,2,3,4,5,6,7,8,9,10) 予約変数__t__ Ver.2.736.107以降、追加 ・ODE高階行列関数||ODEt高階行列関数の時間 予約変数__x__ Ver.2.736.107以降、追加 ・ODE高階行列関数||ODEt高階行列関数の未知変数vector(列vector形式) ・Jacobi高階行列関数||Newton高階行列関数の未知変数vector(列vector形式) Ver.2.739.107以降、追加 Ver.2.158.38以降、実数値のcsv-fileのread機能を追加 予約変数csv連番 ・連番=0~read1回毎に1増加 ・Clear実行確定でreset 予約変数への代入可 clear; ans=1; ans -> 1 ans=<ans; ans=> -> 1 ・ただし、実行確定の都度、上書きされる -1 -> -1 ans -> -1 ans=> -> -1 |
|
目次
変数への 代入 入力仕様 |
変数への代入の入力仕様と付随する留意事項について記述する
代入を括弧で括った場合、0を返す (x=3) -> 0 代入をcomma,||colon:で区切った場合、0を返す clear; x=2,3x -> (0,6) clear; x=2:3x -> (0:6) 詳細は特殊仕様参照 代入のnestingを許容する(括弧より優先の最上位関数を除く) clear; (a=(b=1),{c=2}) -> (0,0) a,b,c -> (0,1,2) clear; {a=((b=1),{c=2})}=(d=3)+1 -> 1 a,b,c,d -> (0,0,1,2,3) clear; ({a=((b=1),{c=b+1})}=(d=c+1)+d) -> 3 a,b,c,d -> (0,0,1,2,3) clear; d={a={(b=1),{c=2}}}; d -> 0 a,b,c,d -> (0,1,2,0:0) |
|
目次
行列要素 pattern matching 入力仕様 |
行列要素pattern matchingの入力仕様と付随する留意事項について記述する
行列要素pattern matchingの定義 ・括弧のnestingを解決後、左辺と右辺の対応する各行列要素を比較 ・Ver.2.269.62以降、遅延評価に対応 ・Ver.2.350.86以降、定義済み行列への代入に対応 ・Ver.2.440.90以降、行列size比較を厳格化 clear; ($a,$b,$c)=(1,2); (a,b) -> ・Ver.2.441.90以降、代入に無関係の要素の比較不可 clear; ($a,$b,3)=(1,2,=<4); (a,b) -> 行列要素pattern matchingによる変数への値の代入規則を列挙する ・変数は無次元 ・変数名symbolにescape記号$を追加して右辺||左辺の値を代入 clear; ($a,{$b,3})=(1,{2,$c}); (a,{b,c}) -> (1,2:0,3) ・再代入も同様 ($a,$b)=1(1,2); (a,b) -> (1,2) ・ clear; ($a,$b,3)=(1,2,=<4); (a,b) -> clear; $a=-1; ($a)=1 || (-1)=1 || =1-(-1) -> 2 clear; ($a)=1; a -> 1 ・Ver.2.249.57以降、再代入と重複宣言を禁止するconst宣言を暫定追加($開始のbeta版) clear; $a=1; a -> 1 clear; $a=1; ($a)=1 -> [MyErr]Invalid SEv-scope-const(a) ・$でescapeしない場合、error終了 clear; (a)=1 -> [MyErr]Invalid REv(a) ・変数に代入する値を解決後、代入 clear; a=1; ($a,$b)=(-1,a); (a,b) -> (-1,1) ・変数に代入する値が存在しない場合、error終了 clear; ($a,$b)=(1,$b) -> [MyErr]Invalid matching clear; ($a,$b)=(1) -> [MyErr]Invalid matching(vars) clear; ($a,(($b)=3))=(1,2) -> [MyErr]Invalid matching(vars) ・左右未解決のmatching不可 ($a,$b)=($c,2) -> [MyErr]Invalid matching(LR) ・変数を含む演算不可 clear; ($a,2)=2(1,$b) -> [MyErr]Invalid FN operation ・変数への代入と判別される場合、左右交換不可 clear; c=<(1,2); ($a,$b)=c; a,b -> (1,2) ・Ver.2.232.56以降、symbol表記に統一 ・Ver.2.246.57以降、name渡しに対応 clear; c=<(1,2); c=($a,$b) -> ・1重列挙の場合 clear; c=<(1,2); (c)=($a,$b); a,b -> (1,2) clear; c=<(1,2); {c}=($a,$b); a,b -> (1,2) ・2重列挙の場合 clear; c=<(1,2); (c,)=($a,$b); a,b -> (1,2) clear; c=<(1,2); (,c)=($a,$b); a,b -> (0,1) clear; c=<(1,2); {c,}=($a,$b); a,b -> (1,2) clear; c=<(1,2); {,c}=($a,$b); a,b -> [MyErr]Invalid matching(vars) ・複数列挙の場合 clear; {($a,$b)=(1,2):($c,$d)=(3,4),(a,b,c,d)} -> (0,0:0,1,2,3,4) ・Ver.2.146.37以降、接頭辞を含む変数への代入不可 clear; ($0xg)=1 -> [MyErr]Invalid varName(0xg) clear; ($0x0g)=1 -> [MyErr]Invalid varName(0x0g) clear; ($0b18)=2 -> [MyErr]Invalid varName(0b18) clear; ($0of)=3 -> [MyErr]Invalid varName(0of) Ver.2.29.15以降、代入のnestingを許容する clear; ($a,(($b)=3))=(1,2); (a,b) -> (1,3) clear; ($a,(($b,($c)=4)=3))=(1,2); (a,b,c) -> (1,3,4) clear; ($a,(($b,($c)=4)=(,3)))=(1,2); (a,b,c) -> (1,0,4) clear; ($a,(($b,($c)={,4})=(,3)))=(1,2); (a,b,c) -> (1,0,0) Ver.2.102.33以降、式変数のargumentsの変数名symbolを未知変数にcountする不具合を解消 clear; f(x)=<x,(1=2) -> (0,1) clear; f(x)=<x,((a=1)=((b=2)=((c=3)=((d=4)+5)))),f(-1)*(a,b,c,d) -> (0,5,-1,-2,-3,-4) clear; f(x)=<x,((a=1)=((b=2)=((c=<3)=((d=<4)+5)))),f(-1)*(a,b,c,d) -> (0,5,-1,-2,-3,-4) clear; f(x)=<x,((a=<1)=((b=<2)=((c=3)=((d=4)+5)))),f(-1)*(a,b,c,d) -> (0,5,-1,-2,-3,-4) clear; f(x)=<x,((a=<1)=((b=<2)=((c=<3)=((d=<4)+5)))),f(-1)*(a,b,c,d) -> (0,5,-1,-2,-3,-4) Ver.2.269.62以降、遅延評価に対応 clear; ($A)=(=<(1,2:3,4)); A -> (1,2:3,4) ・未解決の場合、error終了 clear; ($A)=((x)=<(1,2:3,4)); A -> [MyErr]Invalid args isFound(x) clear; ($A)=(=<(x,2:3,4)); A -> [MyErr]Invalid matching var(A) clear; ($A)=(=<f); A -> [MyErr]Invalid matching var(A) Ver.2.350.86以降、定義済み行列への代入に対応 clear; A=zeros(2); ($A[0][0],$A[1][1])=(1,4); A -> (1,0:0,4) clear; A=zeros(2); ($A[0],$A[1])=(=<(1,1),=<(2,2)); A -> (1,1:2,2) ・Ver.2.373.86以降、行列size指定のindexを厳格化([0] ⇒ 空行列[]) clear; A=(1,2:3,4); ($A[-1][-1][0][0])=(=<A); A -> clear; A=(1,2:3,4); ($A[-1][-1][][])=(=<A); A -> (4,3:2,1) 留意事項を列挙する ・遅延評価の場合、列挙順序に依存するため、非可換 clear; A=(1,2:3,4); ($A[0],$A[][0])=(=<(,),=<{1,1}); A -> (1,0:1,4) clear; A=(1,2:3,4); ($A[][0],$A[0])=(=<{1,1},=<(,)); A -> (0,0:1,4) ・遅延評価の場合、同時交換不可(matching参照) clear; A=(1,2:3,4); ($A[0],$A[1])=(=<A[1],=<A[0]); A // NG -> (3,4:3,4) clear; A=(1,2:3,4); B=A; ($A[0],$A[1])=(=<B[1],=<B[0]); A -> (3,4:1,2) |
|
目次
変数のscope 入力仕様 |
変数のscopeの入力仕様と付随する留意事項について記述する
scope内での変数||式変数の宣言はECMAScript6(以降、ES6と省略する)のlet宣言を想定 直列scope内の変数はreadonly(pollution disabled) scopeから直接、local storageにwriteする場合、最上位関数参照 ・test caseを列挙する clear; [a=2,[a=1,a],a] -> (0,0,1,2) clear; [a=2,=<[a=1,=<a]=>+a]=> -> 3 ・変数・式変数はES6のlet変数同様に宣言時の階層に依存する ・よって同一scope内の変数のみ、変数への代入可 clear; a=3,[a=1,a,a=2,a],a -> (0,0,1,0,2,3) clear; a=3; [a=1,a,a=2,a]; a -> 3 clear; [a=1,a],a -> [MyErr]Invalid REv(a) clear; [a=1,a]; a -> [MyErr]Invalid REv(a) ・行列要素pattern matchingによる変数への代入も同様 clear; a=3,[($a)=1,a,($a)=2,a],a -> (0,0,1,0,2,3) clear; a=3; [($a)=1,a,($a)=2,a]; a -> 3 clear; [($a)=1,a],a -> [MyErr]Invalid REv(a) clear; [($a)=1,a]; a -> [MyErr]Invalid REv(a) ・行列への代入も同様 clear; [A=(1,2),A[0][0]=-1,A] -> (0,0,-1,2) clear; A=(1,2); [A[0][0]=-1,A] -> [MyErr]Invalid SEv-scope(A) ・並列scopeの変数を参照不可 clear; [A=(1,2),],[A] -> [MyErr]Invalid REv(A) clear; ([A=(1,2),],[A]) -> [MyErr]Invalid REv(A) clear; [A=(1,2),],[B=-A,] -> [MyErr]Invalid binary operation clear; ([A=(1,2),],[B=-A,]) -> [MyErr]Invalid binary operation ・直列scope内の変数を参照可 clear; A=(1,2); [A] -> (1,2) clear; A=(1,2); [-A] -> (-1,-2) clear; A=(1,2); [B=-A,B] -> (0,-1,-2) clear; A=(1,2); [B=-A,[C=A+B,C]] -> (0,0,0,0) clear; A=(1,2); [B=-A,[C=A+B,C],C] -> [MyErr]Invalid REv(C) clear; a=3; [($a,{($b)=a})=2,a+b] -> (0,5) ・直列scope内の変数のsearch-precedence clear; A=(1,2); B=A; [B=-B,[C=A+B,C]] -> (0,0,0,0) clear; A=(1,2); B=A; [B=-B,[C=A+B,C]]; B -> (1,2) clear; A=(1,2); B=A; (B=-B,[C=A+B,C]) -> (0,0,0,0) clear; A=(1,2); B=A; (B=-B,[C=A+B,C]); B -> (-1,-2) ・式変数も同様 clear; A=<(1,2); B=<A; [B=<-B,[C=<A+B,C]] -> Maximum call stack size exceeded clear; A=<(1,2); B=<A; [D=-B,B=<D,[C=<A+B,C]] -> (0,0,0,0,0) clear; A=<(1,2); B=<A; [D=-B,B=<D,[C=<A+B,C]]; B -> (1,2) clear; A=<(1,2); B=<A; (D=-B,B=<D,[C=<A+B,C]) -> (0,0,0,0,0) clear; A=<(1,2); B=<A; (D=-B,B=<D,[C=<A+B,C]); B -> (-1,-2) clear; a=<[3+4,]; ([a=>]+[a=>])*trans([a=>]) -> 98 ・宣言時の階層に依存するため、次の場合、error終了 let a=()=>b; (function(){let b=1; return a();})(); // ES6 -> b is not defined clear; a=<b; [b=1,=<a=>]=> -> [MyErr]Invalid REv(b) ・式読出し時の階層を継承する場合、式変数のscope継承callを使用 ・式読出し記号==> clear; a=<b; [b=1,=<a=>]=> -> [MyErr]Invalid REv(b) clear; a=<b; [b=1,=<a==>]=> -> 1 clear; a=<b; [b=1,=<a==>]==> -> 1 ・同義 (function(){let a=()=>b; let b=1; return a();})(); // ES6 -> 1 clear; [a=<b,b=1,=<a=>]=> -> 1 ・let宣言の挙動を以下に比較して示す (function(){let a=()=>b; let c=a(); let b=1; return c;})(); // ES6 -> Cannot access 'b' before initialization clear; [a=<b,c=a=>,b=1,=<c]=> -> [MyErr]Invalid REv(b) let b=-1; (function(){let a=()=>b; let c=a(); let b=1; return c;})(); // ES6 -> Cannot access 'b' before initialization clear; b=-1; [a=<b,c=a=>,b=1,=<c]=> // not hoisted -> -1 let b=-1; (function(){let a=()=>b; let c=a(); return c;})(); // ES6 -> -1 clear; b=-1; [a=<b,c=a=>,=<c]=> -> -1 let b=-1; (function(){let a=()=>b; let b=1; let c=a(); return c;})(); // ES6 -> 1 clear; b=-1; [a=<b,b=1,c=a=>,=<c]=> -> 1 ・最上位関数を使用 clear; b=-1; a=<[b,b]; a=> -> (-1,-1) clear; b=-1; a=<[b,b]; b=1,a=> -> (0,1,1) clear; b=-1; a=<[b,b]; [b=1,a=>] -> (0,-1,-1) clear; a=<b; [b=1,a=>] -> [MyErr]Invalid REv(b) clear; a=<b+1; [b=1,a=>] -> [MyErr]Invalid binary operation clear; a=<[b,b]; [b=1,a=>] -> [MyErr]Invalid REv(b) clear; a=<[b,b]; [b=2,addVar(b),a=>] -> (0,1,2,2) clear; [a=<[b,b],b=1,a=>,b=2,a=>] -> (0,0,1,1,0,2,2) clear; [a=<[b,b],[b=1,],a=>] -> [MyErr]Invalid REv(b) clear; [a=<[b,b],[b=2,addVar(b)],a=>] -> (0,0,1,2,2) clear; b=-1; a=<[b,b]; [[b=1,],a=>] -> (0,0,-1,-1) clear; b=-1; a=<[b,[b,]]; [b=1,a=>] -> (0,-1,-1,0) clear; b=-1; [a=<[b,[b,]],b=1,a=>] -> (0,0,1,1,0) clear; b=-1; [a=<[b,[b,]],[b=1,b],[a=>,b]] -> (0,0,1,-1,-1,0,-1) clear; b=-1; [a=<[b,[b,]],[b=1,b],b=2,[a=>,b]] -> (0,0,1,0,2,2,0,2) clear; b=-1; [a=<(b,[b,[b,]]),b=1,a=>] -> (0,0,1,1,1,0) clear; b=-1; [a=<(b,[b=2,[b,]]),b=1,a=>] -> (0,0,1,0,2,0) clear; b=-1; [a=<(b,[b=2,[b,]]),b=1,=<a=>]=> -> (1,0,2,0) clear; b=-1; a=<(b,[b=2,[b,]]); ([b=1,a=>]) -> (0,-1,0,2,0) ・scopeのnesting clear; a=-1; [a=1,=<a+1]=> -> 2 clear; a=-1; [a=<1,=<a]=> -> -1 clear; a=-1; [a=<1,=<a=>]=> -> 1 clear; a=-1; [[a=<1],=<a=>]=> -> [MyErr]Invalid reference clear; a=-1; [[a=<1,a],=<a=>]=> -> [MyErr]Invalid REv(a) clear; a=<-1; [[a=<1,a],=<a=>]=> -> -1 clear; [a=<1,=<a=>+1]=> -> 2 clear; a=1; [a=2,=<(a,[[a=3,a],a])]=>,a -> (2,0,3,2,1) clear; a=1; [a=2,=<{a,[[a=3,a],a]}]=>,a -> (2,1:0,3,2) clear; a=1; {[a=2,=<{a,[[a=3,a],a]}]}=>,a -> (2,1:0,3,2) clear; a=1; {a=2,=<{a,[[a=3,a],a]}}=>,a -> (2,2:0,3,2) clear; [a=1,(a=2,[a,a=3,a],a=4),a,[a,a=5,a],a] -> (0,0,2,0,3,0,4,4,0,5,4) clear; [a=1,a[0][0]=2,(a,3)] -> (0,0,2,3) clear; a=1,[a=2,[a=3,=<a]=>,a,[a,a],[($a)=4,a]],a -> (0,0,3,2,2,2,0,4,1) clear; a=1,(a=2,[a=3,=<a]=>,a,[a,a],[($a)=4,a]),a -> (0,0,3,2,2,2,0,4,2) clear; a=-1; [a=1,(a=2,[a=3,=<a]=>,a,[a,a],[($a)=4,a]),a],a -> (0,0,3,2,2,2,0,4,2,-1) clear; a=-1; [a=1,(a=2,[a=<3,=<a]=>,a,[a,a],[($a)=4,a]),a],a -> (0,0,2,2,2,2,0,4,2,-1) clear; a=-1; [a=1,(a=2,[a=<3,=<a=>]=>,a,[a,a],[($a)=4,a]),a],a -> (0,0,3,2,2,2,0,4,2,-1) clear; a=-1; [a=1,(a=2,[a=<3,=<a=>]=>,a,[a,a],[($a)=4,a]),=<a]=>,a -> (2,-1) ・式渡しの直接式読出し ・(function(){return (function(){return (function(){var a=1; return 3;})()+a;})()*2;})(); clear; [=<[=<[a=1,=<3]=>+a]=>*2]=> -> [MyErr]Invalid binary operation ・(function(){return (function(){var a=1; return (function(){return 3;})()+a;})()*2;})(); clear; [=<[a=1,=<[=<3]=>+a]=>*2]=> -> 8 ・(function(){var a=1; return (function(){return (function(){return 3;})()+a;})()*2;})(); clear; [a=1,=<[=<[=<3]=>+a]=>*2]=> -> 8 ・var a=1; (function(){return (function(){return (function(){return 3;})()+a;})()*2;})(); clear; a=1; [=<[=<[=<3]=>+a]=>*2]=> -> 8 ・(function(){return (function(){return (function(){var a=1; return 3;})()+1;})()*a;})(); clear; [=<[=<[a=1,=<3]=>+1]=>*a]=> -> [MyErr]Invalid binary operation ・(function(){return (function(){var a=1; return (function(){return 3;})()+1;})()*a;})(); clear; [=<[a=1,=<[=<3]=>+1]=>*a]=> -> [MyErr]Invalid binary operation ・(function(){var a=1; return (function(){return (function(){return 3;})()+1;})()*a;})(); clear; [a=1,=<[=<[=<3]=>+1]=>*a]=> -> 4 ・var a=1; (function(){return (function(){return (function(){return 3;})()+1;})()*a;})(); clear; a=1; [=<[=<[=<3]=>+1]=>*a]=> -> 4 |
|
目次
単独scope 入力仕様 |
単独scopeの入力仕様と付随する留意事項について記述する
Ver.2.32.17以降、式変数のargumentsを追加 ・Ver.2.210.46以降、単独scopeの判定を厳格化(scope_NGのNG範囲を最小化) 式の長さ制限あり ⇒ 長さ制限なし(単独の括弧を探索) ・Ver.2.213.47以降、useScopeWithを追加 ・Ver.2.229.56以降、式変数のargumentsをscope変数から削除しない仕様に変更 ・Ver.2.290.71以降、式変数のargumentsのscope変数保持条件の仕様変更 ・Ver.2.291.71以降、scope変数のsearch-precedenceの仕様変更 単独scopeの場合、式変数のargumentsは角括弧[]のscope内に定義する ・定義の範囲 f(x)=<[,x] f(x)=<last[,x] f(x)=<[=<x]=> f(x)=<[=<x*2]=>x2 ・Ver.2.210.46以降、不都合が発生 fact_(n)=<n<=1|||last[,n*fact_(n-1)]; fact_(10) -> [MyErr]Invalid operation n<=number fact_(n)=<last[,n<=1|||n*fact_(n-1)]; fact_(10) -> 3628800 test caseを列挙する clear; com2vec(a)=<[{real(a),imag(a)}]; com2vec(2-3i) -> (2:-3) clear; minus(a)=<[,=<-a]=>; minus(2) -> -2 clear; add(a,b)=<last[,a+b]; add(1,3) -> 4 clear; f(a,b)=<[()=<[a,b]],(f(1,2))()=>,(a,b) -> [MyErr]Undef var(a) ・以下の場合、外側の括弧を判定するため、単独scopeではない clear; f(a,b)=<(()=<[a,b]),(f(1,2))()=>,(a,b) -> (0,1,2,1,2) clear; f(a,b)=<([()=<[a,b]]),(f(1,2))()=>,(a,b) -> (0,1,2,1,2) ・明示的な代入も同様 clear; f=(x)=<g=<[x,x]; f(3); g() -> [MyErr]Undef var(x) clear; f=(x)=<(g=<[x,x]); f(3); g() -> [MyErr]Undef var(x) f=(x)=<[g=<[x,x],=<g]=>; f(3)=>g; g() -> (3,3) f(5)=>g; g() -> (5,5) 留意事項を列挙する ・以下のような場合、定義元argumentsは角括弧[]のscope外に定義する clear; minus_k(a,k)=<[,=<-a]=>*k; minus_k(2,2) -> -4 clear; add_k(a,b,k)=<last[,a+b]*k; add_k(1,3,2) -> 8 ・Ver.2.210.46以降、定義不能 clear; com2vec_k(a,k)=<[{real(a),imag(a)}]*k; com2vec_k(2-3i,i) -> [MyErr]Invalid binary operation clear; minus_k(a,k)=<[,=<-a]=>*k; minus_k(2,2) -> [MyErr]Invalid binary operation clear; add_k(a,b,k)=<last[,a+b]*k; add_k(1,3,2) -> [MyErr]Invalid binary operation ・丸括弧()明示で引数を経由する場合、角括弧[]のscope外に定義 clear; f(x)=<[=<x]()=>; f(3) -> 3 clear; f(x)=<[(x)=<x](x)=>; f(3) -> 3 clear; iproduct(L,R)=<[(LR)=<LR](=<L*R.)=>; iproduct(=<(1,2),=<(3,4)) -> 11 ・複数列挙の場合、角括弧[]のscope外に定義 clear; iproduct(L,R)=<[L]*[trans(R)]; iproduct(=<(1,2),=<(3,4)) -> 11 clear; iproduct(L,R)=<[(L)][trans(R)]; iproduct(=<(1,2),=<(3,4)) -> 11 clear; iproduct(L,R)=<[(L)](trans(R)); iproduct(=<(1,2),=<(3,4)) -> 11 clear; iproduct(L,R)=<(L)[trans(R)]; iproduct(=<(1,2),=<(3,4)) -> 11 clear; iproduct(L,R)=<(L)(trans(R)); iproduct(=<(1,2),=<(3,4)) -> 11 |
|
目次
式変数 入力仕様 |
式変数の入力仕様と付随する留意事項について記述する
式変数への代入・再代入方法 式変数名=<方程式||関数式||展開式 ・式代入記号=<(式渡しに流用するため、一般的な記号:=で代替不可) ・式変数への代入を以降、式代入と呼ぶ test caseを列挙する y=<{a*x+b=0}; -> stored_eqn(y) y=<a*x+b=0; -> stored_eqn(y) y=<{a*x+b}; -> stored_eqn(y) y=<a*x+b; -> stored_eqn(y) ・null-rightの場合、error終了 =< -> [MyErr]Invalid =<null ・Ver.2.27.15以降、null代入不可 x=<; x -> [MyErr]Invalid =<null ・式変数は変数の命名規則に準拠 ・Ver.2.249.57以降、再代入と重複宣言を禁止するconst宣言を暫定追加($開始のbeta版) |
|
目次
式読出し 入力仕様 |
式読出しの入力仕様と付随する留意事項について記述する
式変数から値を読出す方法 式変数名=> ・式変数からの値読出しを以降、式読出しと呼ぶ y=<a*x+b; y=> -> [MyErr]Invalid binary operation ・Ver.2.27.15以降、null-leftの場合、error終了 => -> [MyErr]Invalid null=> Ver.2.31.17以降、式変数のscope継承callの式読出し記号==>を追加 clear; a=<1; a=> -> 1 clear; a=<1; a==> -> 1 clear; a=<1; a==>2 || 1(2) -> 2 ・Ver.2.119.34以降、left-operand不正の場合、error終了 clear; a=<1; a===> -> [MyErr]Invalid BRrl(==) clear; a=<1; a====> -> [MyErr]Invalid BRrl(==) 関数式の変数を定義して再度読出す y=<a*x+b; a=1; b=2; x=3; y=> || 1*3+2 -> 5 ・式読出しを括弧で括れば変数同様に扱える 2; y=<ans; max(3,4(y=>)2) || max(3,4*2*2) -> 16 式変数と同名の変数が未定義の場合、直接、式読出し可 clear; y=<a*x+b; a=1; b=2; x=3; 2y -> 10 clear; y=<a*x+b; a=1; b=2; x=3; y0=2y; y0 -> 10 ・ただし、式読出し記号=>を明示する方が間違いが少ない y=-1; y=<a*x+b; a=1; b=2; x=3; 2y -> -2 y=-1; y=<a*x+b; a=1; b=2; x=3; 2(y=>) -> 10 ・さらに、式変数名と変数名は区別する方が間違いが少ない y=3; y=<3y-1; 2y -> 6 ・Ver.2.203.46以降、変数への式読出しの仕様を廃止して式変数への式読出しを追加 y=3; y=<3y-1; y=>y; 2y -> 6 式変数名で明示して直接読出す方法もあり得る clear; eqn_x=<(a*x+b=0); a=1; b=2; x=3; 2eqn_x || 2*(-5) -> -10 以降、変数名と式変数名は被らない前提で式読出し記号=>を省略する |
|
目次
変数への 式読出し 入力仕様 |
変数への式読出しの入力仕様と付随する留意事項について記述する
・本仕様は以下の理由から廃止の可能性がある 変数への代入と冗長 多重代入不可のため、読出し値が残る唯一の仕様は無駄仕様 ・Ver.2.203.46以降、本仕様を廃止して式変数への式読出しを追加 式変数名=>変数名 y=<a*x+b; y=>y0 -> [MyErr]Invalid binary operation y=<a*x+b; a=1; b=2; x=3; y=>y0; y0 -> 5 y0=3; y=<3y0-1; y=>y1; 2y1 -> 16 clear; a=<1; a==>b; b -> 1 ・変数への代入と異なり、読出し値が残る 2; y=<ans; max(3,4(y=>y0)2); y=> -> 16 ・式渡しの直接式読出しで使用する場合、読出し値の次元が残らないように留意する clear; [v=<(1,2),v=v=>,=<v]=> // OK -> (1,2) clear; [v=<{1,2},v=v=>,=<v]=> // OK -> (1:2) clear; [v=<(1,2),v=>v,=<v]=> // NG -> (1,2) clear; [v=<{1,2},v=>v,=<v]=> // NG -> [MyErr]Invalid mat([object Object]) clear; [v=<{1,2},v=v=>v,=<v]=> -> (1:2) clear; [a=1,b=2,last{v=<{a,b},v=>v},a=-1,b=-2,=<v]=> -> (1:2) clear; [a=1,b=2,last{v=<{a,b},v=>v},a=-1,b=-2,=<v=>]=> -> (-1:-2) clear; [a=1,b=2,v=<{a,b},v=v=>v,a=-1,b=-2,=<v]=> -> (1:2) clear; [a=1,b=2,v=<{a,b},v=v=>v,a=-1,b=-2,=<v=>]=> -> (-1:-2) |
|
目次
式変数への 式読出し 入力仕様 |
式変数への式読出しの入力仕様と付随する留意事項について記述する
・Ver.2.203.46以降、変数への式読出しの仕様を廃止して追加 ・Ver.2.204.46以降、式読出しの仕様を仮fix 無名callはcall結果が解決済みの前提で非対応 symbol渡しの前提で参照透過性なし ・Ver.2.211.46以降、式読出しの仕様をfix 無名callの式読出しに対応 symbol渡しの参照透過性を確保 ・Ver.2.229.56以降、式変数のargumentsをscope変数から削除しない仕様に変更 ・Ver.2.290.71以降、式変数のargumentsのscope変数保持条件の仕様変更 ・Ver.2.291.71以降、scope変数のsearch-precedenceの仕様変更 ・Ver.2.229.56以降、変数の命名規則に準拠 ・Ver.2.232.56以降、symbol表記に統一 [=<$g]=>f; f=> -> [MyErr]Invalid ・Ver.2.253.59以降、式変数の新規複製の仕様廃止 式変数名=<式変数名による新規複製は後方互換性(f=<x等)のため、非対応(symbol渡しを除く) 式変数名=>式変数名 clear; g=<x; g=>f; x=1; f=> -> 1 clear; g=<x; g=>f; x=1; f=f=>; f,g=>,f=> -> (1,1,1) clear; g=<x; g=>f; x=1; f=f=>; x=2; f,g=>,f=> -> (1,2,2) clear; g(x)=<x; g=>f; f(3)=> -> 3 ・scopeはstatic scopes2d arrayを共有する clear; scope_NG(x)=<last[x=x,last[x=x,x]]; scope_NG(3),scope_NG=>f,f(4) -> (3,0,3) ・call結果の式読出し clear; g(x)=<x; g(3)=> -> 3 clear; [(x)=<x](3)=> -> 3 ・var g = function(x){return x;}; var f = g(3); f; clear; g(x)=<x; f=g(3)=>; f -> 3 ・var g = function(x){return x;}; var f = function(){return g(3);}; f(); clear; g(x)=<x; g(3)=>f; f=> -> 3 ・var f = (function(x){return x;})(3); f; clear; f=[(x)=<x](3)=>; f -> 3 ・var f = function(){return (function(x){return x;})(3);}; f(); clear; [(x)=<x](3)=>f; f=> -> 3 ・Ver.2.211.46以降、var f = function(){return (function(x){return x;});}; f(3); clear; [()=<(x)=<x]()=>f; f(3)=> -> 3 clear; [=<(x)=<x]=>f; f(3)=> -> 3 clear; [=<[((x))=<((x))]]=>f; f(3)=> -> 3 ・Ver.2.211.46以降、var f = (function(a){return (function(x){return a*x;});})(-1); f(3); clear; [a=-1,=<(x)=<a*x]=>f; f(3)=> -> -3 ・Ver.2.229.56以降、式変数のargumentsをscope変数から削除しない仕様に変更 ・Ver.2.290.71以降、式変数のargumentsのscope変数保持条件の仕様変更 ・Ver.2.291.71以降、scope変数のsearch-precedenceの仕様変更 clear; [(a)=<(x)=<a*x](-1)=>f; f(3)=> -> -3 ・Ver.2.213.47以降、useScopeWith選択の場合 clear; [(a)=<(x)=<a*x](-1)=>f; a=1; f(3)=>,f(3)==> -> (-3,3) ・式渡しの直接式読出し(Ver.2.195.45以降、無名callのarguments省略) clear; [f(x)=<x,=<f]=> -> [MyErr]Invalid null=> ・var f = (function(){var f = function(x){return x;}; return f;})(); f(3); clear; [f(x)=<x,=<f]=>f; f(3)=> -> 3 ・symbol渡し clear; (x=-1,g=<x,=<g)=> -> -1 clear; (x=-1,g=<x,=<g)=>f; x=1; f=> -> 1 clear; [x=-1,g=<x,=<g]=>f; x=1; f=> -> -1 clear; (a=-1,g(x)=<a*x,=<g)=> -> [MyErr]Invalid null=> clear; (a=-1,g(x)=<a*x,=<g)=>f; a=1; f(3)=> -> 3 ・var f = (function(){var a = -1; var g = function(x){return a*x;}; return g;})(); var a = 1; f(3); clear; [a=-1,g(x)=<a*x,=<g]=>f; a=1; f(3)=> -> -3 ・式変数のargumentsをscope内に残す場合、変数名を区別して代入を明示 clear; make_f(a)=<[g(x)=<a*x,=<g]=>f; make_f(-1); a=1; f(3)=>,f(3)==> -> (3,3) clear; make_f(a0)=<[a=a0,g(x)=<a*x,=<g]=>f; make_f(-1); a=1; f(3)=>,f(3)==> -> (-3,3) ・var f = (function(){var a = -1; return function(x){return a*x;};})(); var a = 1; f(3); clear; [a=-1,=<a*x]=>f; a=1; f=> -> [MyErr]Invalid binary operation clear; [a=-1,=<=<a*x]=>f; a=1; f=> -> [MyErr]Invalid BTe([object Object],[object Object],[object Object]) clear; [a=-1,=<(x)=<a*x]=>f; a=1; f(3)=> -> [MyErr]Invalid args.length=0(f) ・Ver.2.211.46以降、参照透過性を確保 clear; [a=-1,f(x)=<a*x,=<f]=>f; a=1; f(3)=> -> -3 clear; [a=-1,=<(x)=<a*x]=>f; a=1; f(3)=> -> -3 clear; [a=-1,=<{(x)=<(a*x)}]=>f; a=1; f(3)=> -> -3 clear; [a=-1,f(x)=<a*x,=<{f}]=>f; a=1; f(3)=> -> [MyErr]Invalid null=> ・scope継承call clear; [x=-1,g=<x,=<g]=>f; x=1; f==> -> 1 clear; [x=-1,g=<x,=<g]==>f; x=1; f=> -> 1 clear; [a=-1,g(x)=<a*x,=<g]=>f; a=1; f(3)==> -> 3 clear; [a=-1,g(x)=<a*x,=<g]==>f; a=1; f(3)=> -> 3 ・scope変数は演算実行確定1回毎に初期化のため、再利用不可 clear; [a=-1,=<(x)=<a*x]=>f; f(3)=> -> -3 f(3)=> -> [MyErr]Invalid binary operation ・scope-ids初期化のため、再利用の場合、変数を新規定義 a=1; f(3)=> -> 3 ・変数への代入||symbolic高階行列関数同様に、0を返す clear; a=<1; a=>b -> 0 clear; a=<1; a==>b -> 0 clear; [v=<{1,2},v=v=>v,=<v]=> -> 0 ・式代入の場合、括弧が必要 clear; make_f(hasMinus)=<[hasMinus&&&(f(x)=<-x)||||(f(x)=<x),=<f]=>f; make_f(false)=>,f(1)=>,make_f(true)=>,f(1)=> -> (0,0,1,0,-1) ・式読出しの場合、括弧が不要 clear; fm(x)=<-x,fp(x)=<x,make_f(hasMinus)=<[hasMinus&&&fm=>f||||fp=>f,=<f]=>f; make_f(false)=>,f(1)=>,make_f(true)=>,f(1)=> -> (0,0,1,0,-1) ・switch高階関数の場合、implicit Euler_method参照 clear; make_f(hasMinus)=<switch(hasMinus,=<f(x)=<-x:1,=<f(x)=<x); make_f(false)=>,f(1)=>,make_f(true)=>,f(1)=> -> (0,0,1,0,-1) test caseを列挙する ・Ver.2.253.59以降、式変数の新規複製の仕様廃止 clear; [v=<{1,2},v=>v,=<v]=> -> (1:2) clear; [a=1,b=2,last{v=<{a,b},v=>v},a=-1,b=-2,=<v]=> -> (-1:-2) clear; [a=1,b=2,last{v=<{a,b},v=>v},v=v=>,a=-1,b=-2,=<v]=> -> (1:2) clear; [a=1,b=2,last{v=<{a,b},v=>v},a=-1,b=-2,=<v=>]=> -> (-1:-2) clear; [a=1,b=2,last{v=<{a,b},v=>v0},a=-1,b=-2,=<v=>]=> -> (-1:-2) clear; [a=1,b=2,v=<{a,b},v=v=>v,a=-1,b=-2,=<v]=> -> 0 clear; [a=1,b=2,v=<{a,b},v=v=>v,a=-1,b=-2,=<v=>]=> -> (-1:-2) clear; g(x)=<a*x; a=1,[a=2,=<(x)=<[a=3,=<g(x)=>]=>]=>f; f(-1)=>,f(-1)==> -> (-1,-1) clear; g(x)=<a*x; a=1,[a=2,=<(x)=<[a=3,=<g(x)=>]==>]=>f; f(-1)=>,f(-1)==> -> (-1,-1) clear; g(x)=<a*x; a=1,[a=2,=<(x)=<[a=3,=<g(x)==>]=>]=>f; f(-1)=>,f(-1)==> -> (-3,-3) |
|
目次
式渡し 入力仕様 |
式渡しの入力仕様と付随する留意事項について記述する
関数の引数に式を渡す場合、値渡しに対して式渡しと定義する ・この場合の関数を高階関数と定義する 式渡しの方法(式代入記号=<を流用) =<式変数名symbol||展開式 ・Ver.2.32.17以降、式変数のargumentsを追加 (args)=<式変数名symbol||展開式 Ver.2.30.15以降、関数の引数に限定して、式代入同様に、式渡しの仕様を緩和 ・総和高階関数を使用 ・次の場合、式変数名symbolと判別する clear; _sn(=<n,0,2) -> [MyErr]Invalid =<eqn clear; n=1; _sn(=<n,0,2) -> [MyErr]Invalid =<eqn clear; n=<n; _sn(=<n,0,2) || 0+1+2 -> 3 ・次の場合、dummy変数と判別する clear; _sn(=<{n},0,2) || 0+1+2 -> 3 clear; n=2; _sn(=<{n},0,2) || 0+1+2 -> 3 ・次の場合、括弧省略と判別する clear; _sn(=<n+1,0,2) || _sn(=<{n+1},0,2) || 1+2+3 -> 6 clear; n=<n; _sn(=<n=>,0,2) || _sn(=<{n=>},0,2) || 0+1+2 -> 3 ・次の場合、括弧省略と判別する clear; _sn(=<1,0,2) || _sn(=<{1},0,2) || 1+1+1 -> 3 留意事項を列挙する ・式代入同等の演算のprecedence 実装の詳細は内部仕様参照 |
|
目次
直接式読出し 入力仕様 |
直接式読出しの入力仕様と付随する留意事項について記述する
Native無名関数を代替する式渡しの直接式読出し(Ver.2.195.45以降、無名callのarguments省略) ・記号の定義 pass記号:=< ⇔ 遅延評価のreturn call記号:=> ⇔ 関数callの丸括弧() ・(function(){return 3;})(); (=<3)=> || {=<3}=> -> 3 (=<{3})=> || {=<{3}}=> -> 3 =<3=> || =<(3)=> || =<{3}=> -> [MyErr]Invalid BTe([object Object],[object Object]) 3=> || (3)=> || {3}=> -> [MyErr]Invalid mat([object Object]) clear; a=3; a=> -> [MyErr]Invalid REv(a) clear; a=3; (a)=> || {a}=> -> [MyErr]Invalid mat([object Object]) clear; a=3; [a]=> -> [MyErr]Invalid reference ・(function(){1; 2; return 3;})(); (1,2,=<3)=> || {1,2,=<3}=> -> 3 ・最終要素が値の場合、error終了 (1,2,3)=> || {1,2,3}=> -> [MyErr]Invalid mat([object Object]) ((,:,),=<1)=> -> [MyErr]Invalid mat([object Object]) ((,:,):=<1)=> -> 1 ・(function(){var a=1; var b=2; var c=3; return [a,b,c];})(); (a=1,b=2,c=3,=<(a,b,c))=> -> (1,2,3) {a=1,b=2,c=3,=<(a,b,c)}=> -> (1,2,3) ・(function(){return 0; return 1;})(); (=<0,=<1)=> -> 1 (=<0,=<1,2)=> -> [MyErr]Invalid mat([object Object]) ・複数列挙の場合、末尾returnのみ取り出す(途中return不可) [a=1,=<a=2,=<a=3,=<a]=> || [a=1,=<a]=> -> 1 (=<(,:,),=<1)=> || (,=<1)=> -> 1 (=<(,:,):=<1)=> || (:=<1)=> -> 1 ・last行列関数は最終要素のみ取り出す clear; (x=(1,2),=<x)=> -> (1,2) clear; {x=(1,2:3,4),x=-x,=<x}=> -> (-1,-2:-3,-4) clear; last(x=(1,2),x) -> 2 clear; last{x=(1,2:3,4),x=-x,x} -> -4 ・式変数の場合も同様 clear; f=<{x}; x=(1,2); f=> -> (1,2) clear; (f=<{x},x=(1,2),=<f)=> -> (1,2) clear; (f=<{x},x=(1,2),f) -> (0,0,1,2) clear; (f=<{x},x=(1,2),f)=> -> [MyErr]Invalid mat([object Object]) clear; last(f=<{x},x=(1,2),f) -> 2 clear; last(f=<{x},x=(1,2),=<f) -> [MyErr]Invalid BTe([object Object]) clear; (f=<{x},x=(1,2),=<f) -> [MyErr]Invalid BTe([object Object]) clear; (f=<{x},x=(1,2),eqn_f=<f); eqn_f -> (1,2) ・strict-modeの場合、式変数の式読出し記号=>省略不可(式変数のreturn不可) clear; a=1; (=<a)=> -> 1 clear; a=<2; (=<a)=> -> [MyErr]Invalid REv(a) clear; a=1; a=<2; (=<a)=> -> 1 clear; a=1; a=<2; (=<a=>)=> -> 2 clear; (f=<{x},x=(1,2),=<f)=> -> [MyErr]Invalid REv(f) clear; (f=<{x},x=(1,2),=<f=>)=> -> (1,2) clear; (f=<x,x=(1,2),=<f=>)=> -> (1,2) clear; (f=<x,x=<(1,2),=<f=>)=> -> [MyErr]Invalid REv(x) clear; (f=<x=>,x=<(1,2),=<f=>)=> -> (1,2) clear; (f=<{x=>},x=<(1,2),=<{f=>})=> -> (1,2) clear; (f=<{(x=>)},x=<(1,2),=<{(f=>)})=> -> (1,2) Ver.2.27.15以降、式渡しの直接式読出しのnestingに対応 clear; (f=<{(x=>)},x=<(1,2),=<{=<{(f=>)}}=>)=> -> (1,2) ・debuggerなしで無名関数の最短表記を許容 ・(function(){return (function(){return (function(){return 3;})();})();})(); (=<(=<(=<3)=>)=>)=> -> 3 ・(function(){return (function(){return (function(){return 3;})()+1;})()+2;})(); (=<(=<(=<3)=>+1)=>+2)=> -> 6 ・var a=3; (function(){return (function(){return (function(){return a;})();})();})(); clear; a=3; (=<(=<(=<{a})=>)=>)=> -> 3 clear; a=<3; (=<(=<(=<{a=>})=>)=>)=> -> 3 ・var a=[1,2]; (function(){1; return (function(){1; return (function(){1; return a;})();})();})(); clear; a=(1,2); (1,=<(1,=<(1,=<{a})=>)=>)=> -> (1,2) clear; a=<(1,2); (1,=<(1,=<(1,=<{a=>})=>)=>)=> -> (1,2) ・(function(){return (function(){var a=1; return (function(){return 3;})()+a;})()*2;})(); clear; (=<(=<(a=1,=<3)=>+a)=>*2)=> -> 8 clear; (=<(a=1,=<(=<3)=>+a)=>*2)=> -> 8 clear; (a=1,=<(=<(=<3)=>+a)=>*2)=> -> 8 clear; a=1,(=<(=<(=<3)=>+a)=>*2)=> -> (0,8) ・(function(){var a=1; return (function(){return (function(){return 3;})()+1;})()*a;})(); clear; (=<(=<(a=1,=<3)=>+1)=>*a)=> -> 4 clear; (=<(a=1,=<(=<3)=>+1)=>*a)=> -> 4 clear; (a=1,=<(=<(=<3)=>+1)=>*a)=> -> 4 clear; a=1,(=<(=<(=<3)=>+1)=>*a)=> -> (0,4) |
|
目次
式変数への 式代入 入力仕様 |
式変数への式代入の入力仕様と付随する留意事項について記述する
・再帰高階関数で代替のrecursive call非対応(call stackの独自実装なし) clear; a=<a; a -> clear; a=<{a}; a -> clear; a=<a=>; a -> clear; a=<{a=>}; a -> ・strict-modeの場合 clear; a=<a=>; a=> -> clear; a=<{a=>}; a=> -> Ver.2.19.6以降、関数のre-nameの仕様を廃止(無駄仕様と判断) clear; tr=<trans; tr(1,2:3,4) || (tr=>)(1,2:3,4) -> (1,3:2,4) clear; htr=<htrans; htr((htr(i,2i:3i,4i))[1]) -> (2i:4i) clear; tr=<trans; tr[2] -> [MyErr]Invalid FNm(transpose) clear; trans=<trans -> [MyErr]Invalid FNm(transpose) ・高階関数の場合 clear; d=<_d -> [MyErr]Invalid FNh called clear; dx=<_dx; dx(=<{x^2},1,2) -> 3.999999999999929+3.5537737875913754e-14i+O(2e-11+1e-12i) 式代入を括弧で括った場合、0を返す (x=<3) -> 0 式代入をcomma,||colon:で区切った場合、0を返す clear; x=<2,3x -> (0,6) clear; x=<2:3x -> (0:6) 詳細は特殊仕様参照 式変数を式代入可 ・式読出し記号=>を明示する場合 clear; eqn_x=<3x; eqn_y=<(eqn_x=>); x=3; eqn_y=> -> 9 clear; a=<1; b=<a=>; b=> -> 1 clear; a=<1; b=<a=>; (b)=> -> [MyErr]Invalid mat([object Object]) clear; a=<1; b=<a=>; (=<{b=>})=> -> 1 clear; a=<1; b=<a=>; (=<b=>)=> -> 1 clear; a=<1; b=<a=>; =<b=> -> [MyErr]Invalid BTe([object Object],[object Object]) ・同名の変数未定義の前提で式読出し記号=>を省略する場合 clear; eqn_x=<3x; eqn_y=<eqn_x; x=3; eqn_y -> 9 clear; a=<1; b=<a; b -> 1 clear; a=<1; b=<a; (=<b)=> -> 1 式代入のnestingを一例に示す ・式変数aのみ定義される clear; (a=<(b=<{c=<2})); b -> [MyErr]Invalid REv(b) clear; (a=<(b={c=2})); b -> [MyErr]Invalid REv(b) ・式変数aとbを順番に実行することで式変数cが定義される clear; (a=<(b=<{c=<2})); a,c -> [MyErr]Invalid REv(c) clear; (a=<(b=<{c=<2})); a,b -> (0,0) clear; (a=<(b=<{c=<2})); a,b,c -> (0,0,2) ・式変数aを実行することで変数bとcが定義される clear; (a=<(b={c=2})); a,c -> (0,2) clear; (a=<(b={c=2})); a,b -> (0,0) clear; (a=<(b={c=2})); a,b,c -> (0,0,2) ・以下、同様 clear; {a=<((b=<1),{c=<2})}=(d=<3)+1; a,b,c,d -> (0,0,1,2,3) clear; ({a=<((b=<1),{c=<b+1})}=(d=<c+1)+d) -> [MyErr]Invalid binary operation clear; ({a=<((b=<1),{c=<b+1})}=(d=<c+1)); d -> [MyErr]Invalid binary operation clear; ({a=<((b=<1),{c=<b+1})}=(d=<c+1)); a,b,c,d -> (0,0,1,2,3) clear; d=<{a=<{(b=<1),{c=<2}}}; a -> [MyErr]Invalid REv(a) clear; d=<{a=<{(b=<1),{c=<2}}}; d,b -> [MyErr]Invalid REv(b) clear; d=<{a=<{(b=<1),{c=<2}}}; d,c -> [MyErr]Invalid REv(c) clear; d=<{a=<{(b=<1),{c=<2}}}; d,a,b,c -> (0,0,1,2:0,0) 応用例はplot2d-command参照 |
|
目次
scope 継承pass 入力仕様 |
式変数のscope継承passの入力仕様と付随する留意事項について記述する
Ver.2.219.50以降、式渡し記号==<を追加 |
|
目次
scope 継承call 入力仕様 |
式変数のscope継承callの入力仕様と付随する留意事項について記述する
直列scope内の式変数をcallする際、式読出し時の階層を継承する場合 ・式変数のscope継承callと定義する ・Nativeの.call(this)を想定するが、 ・thisの直列scope内のupper-scopeを含めて継承後、callする点で異なる ・Ver.2.830.140以降、無名callのscope継承の不具合を修正 clear; f=<a=1; [f==>,hass(a)],hass(a) -> (0,true,false) clear; arr_f=(()=<a=1); [(arr_f[0])==>,hass(a)],hass(a) -> clear; [g(x)=<x,=<g]=>f; f(2) -> 2 clear; [g(x)=<x,=<g]==>f -> Ver.2.31.17以降、追加の式読出し記号==>を使用 ・test caseを列挙する clear; a=<b; [b=1,=<a=>]=> -> [MyErr]Invalid REv(b) clear; a=<b; [b=1,=<a==>]=> -> 1 clear; a=<b; [b=1,=<a==>]==> -> 1 clear; a=<b; [b=1,=<[=<a==>]=>]=> -> 1 clear; a=<b; [=<[b=1,=<a==>]=>]=> -> 1 clear; a=<b; [b=2,=<[b=1,=<a==>]=>+a=>]=> -> [MyErr]Invalid BRsa operation clear; a=<b; [b=2,=<[b=1,=<a==>]=>+a==>]=> -> 3 clear; a=<b; [b=3,=<[b=2,=<[b=1,=<a==>]=>+a==>]=>+a==>]=> -> 6 clear; a=<b+c; [c=2,=<[b=1,=<a==>]=>]=> -> 3 clear; a=<b+c+d; d=3; [c=2,=<[b=1,=<a==>]=>]=> -> 6 clear; a=<b+c+d; [d=3, c=2,=<[b=1,=<a==>]=>]=> -> 6 clear; [a=<b+c+d, d=3, c=2,=<[b=1,=<a==>]=>]=> -> 6 clear; [d=3, c=2,=<[a=<b+c+d, b=1,=<a==>]=>]=> -> 6 ・Ver.2.90.32以降、sum関数を追加 clear; a=<sum(b,c,d); d=3; [c=2,=<[b=1,=<a=>]=>]=> -> [MyErr]Invalid BRsa operation clear; a=<sum(b,c,d); d=3; [c=2,=<[b=1,=<a==>]=>]=> -> 6 ・Ver.2.32.17以降、式変数のargumentsを追加 clear; a(b,c,d)=<sum(b,c,d); d=3; [c=2,=<[b=1,=<a(b,c,d)=>]=>]=> -> 6 clear; a(b,c,d)=<b+c+d; d=3; [c=2,=<[b=1,=<a(b,c,d)=>]=>]=> -> 6 clear; a(b,c,d)=<b+c+d; d=3; [c=2,=<[b=1,=<a=>]=>]=> -> [MyErr]Invalid binary operation clear; a(b,c,d)=<b+c+d; d=3; [c=2,=<[b=1,=<a==>]=>]=> -> 6 clear; a=<last[s=b+c+d,s]; d=3; [c=2,=<[b=1,=<a==>]=>]=> -> 6 clear; a=<last[s=b+c+d,last[,-s]]; d=3; [c=2,=<[b=1,=<a==>]=>]=> -> -6 clear; a=<last[s=b+c+d,last[,-s]]; d=3; [c=2,=<[b=1,=<a==>]=>]=> -> -6 clear; a=<last[s=b+c+d,last[,-s]]; d=3; [c=2,=<[c=-c,b=1,=<a==>]=>]=> -> -2 clear; a=<last[s=b+c+d,last[,-s]]; d=3; [c=-d,=<[b=1,=<a==>]=>]=> -> -1 clear; a=<last{s=b+c+d,last[,-s]}; d=3; [c=2,=<[b=1,=<a==>]=>]=> -> -6 clear; a=<last{d=-100,s=b+c+d,last[,-s]}; d=3; [c=2,=<[b=1,=<a==>]=>]=> -> 97 ・callする式変数の0階層に宣言される変数はcall先scopeに定義する clear; a=<last{d=-100,s=b+c+d,last[,-s]}; d=3; [c=2,=<[b=1,a==>,=<d]=>]=> -> -100 clear; a=<last{d=-100,s=b+c+d,last[,-s]}; [c=2,=<[d=3,b=1,a==>,=<d]=>]=> -> -100 clear; [a=<last{d=-100,s=b+c+d,last[,-s]},c=2,=<[d=3,b=1,a==>,=<d]=>]=> -> -100 ・callする式変数の1階層に宣言される場合、call先から参照不可 clear; a=<last[d=-100,s=b+c+d,last[,-s]]; [c=2,=<[d=3,b=1,a==>,=<d]=>]=> -> 3 clear; [a=<last[d=-100,s=b+c+d,last[,-s]],c=2,=<[d=3,b=1,a==>,=<d]=>]=> -> 3 ・scope継承callのnesting clear; a=<b; b=0; last[b=1,c=<a=>,[b=2,c=>]] -> 0 clear; a=<b; b=0; last[b=1,c=<a=>,[b=2,c==>]] -> 0 clear; a=<b; b=0; last[b=1,c=<a==>,[b=2,c=>]] -> 1 clear; a=<b; b=0; last[b=1,c=<a==>,[b=2,c==>]] -> 2 clear; a=<b==>; b=<0; last[b=<1,c=<a==>,[b=<2,c==>]] -> 2 実装logicのtest caseを以下に示す ・式変数s0のcall後、scopes2d arrayの各scopeに各変数が定義されることを確認する clear; s0=<[s1=1,[s1,s2=2,[s2,s3=3,[s3,s4=4,[s4,s5=5]]]]]; s0=> -> (0,1,0,2,0,3,0,4,0) clear; s0=<[s1=1,[s1,s2=2,[s2,s3=3,[s3,s4=4,[s4,s5=5]]]]]; [s0=>,] -> (0,1,0,2,0,3,0,4,0,0) ・式変数s2のcall後、scopes2d arrayの各scopeに各変数が定義されることを確認する clear; s0=0,[s1=1,[s2=<[s3=s1+2,[s4=s3+1,s4]],[s5=last[s2==>],s5]]] -> (0,0,0,0,4) ・式変数s0の通常call=>の場合、変数s0はlocal storageに定義される clear; s0=<s0=[s1=1,[s1,s2=2,[s2,s3=3]]]; [s0=>,s0,hasVar(s0),hasV(s0)] -> (0,0,1,0,2,0,1,1) ・式変数s0のscope継承call==>の場合、変数s0はscope内に定義される clear; s0=<s0=[s1=1,[s1,s2=2,[s2,s3=3]]]; [s0==>,s0,hasVar(s0),hasV(s0)] -> (0,0,1,0,2,0,0,1) 詳細は変数のscope内部仕様参照 |
|
目次
scope 継承call の補足 |
式変数のscope継承callの補足について記述する
式変数のscope継承callの仕様を列挙する ・変数・式変数は宣言時の階層に依存するため、次の場合、error終了 let a=()=>b; (function(){let b=1; return a();})(); // ES6 -> b is not defined clear; a=<b; [b=1,=<a=>]=> -> [MyErr]Invalid REv(b) ・式変数のscope継承callを使用して式読出し時の階層を継承する clear; a=<b; [b=1,=<a==>]=> -> 1 ・式変数のargumentsを使用して式変数のscope継承callを代替する clear; a(b)=<b; [b=1,=<a(b)=>]=> // better -> 1 ・式変数の定義元に対してcall先と区別する ・定義元argumentsの変数名symbolは独立する 詳細は未実装の参照渡し参照 clear; a(b)=<last(b=-1,b); (b=1,a(b)=>,b) -> (0,-1,1) clear; a(B)=<{B[0]=B[1],=<B}=>; B=(1,2:3,4); (B,a(=<B)=>,B) -> ( 1,2,3,4,1,2: 3,4,3,4,3,4 ) Ver.2.33.18以降、定義元argumentsの変数は宣言時の階層に依存する(Ver.2.70.28追記) ・定義元とcall先のscopeが同一の場合 ・symbol渡しの場合、定義元とcall先のAは同一 clear; add(A,B)=<A+B; A=(1,2:3,4); add(=<A,=<A) -> (2,4:6,8) clear; add(A,B)=<A+B; A=(1,2:3,4); add(=<A[0],=<A[1]) -> [MyErr]Invalid reference of array clear; add(A,B)=<A+B; A=<(1,2:3,4); add(=<A[0],=<A[1]) -> [MyErr]Invalid reference of array ・Ver.2.71.29以降、定義元argumentsの変数・式変数の初期化algorithmを修正 clear; add(A,B)=<A+B; A=(1,2:3,4); add(=<A[0],=<A[1]) -> (4,6) clear; add(A,B)=<A+B; A=<(1,2:3,4); add(=<A[0],=<A[1]) -> (4,6) ・定義元argumentsの変数名symbolを区別する場合 clear; add(A_,B_)=<A_+B_; A=(1,2:3,4); add(=<A[0],=<A[1]) -> (4,6) clear; add(A_,B_)=<A_+B_; A=<(1,2:3,4); add(=<A[0],=<A[1]) -> (4,6) ・変数と式変数の変数名symbolを区別する場合 clear; add(A,B)=<A+B; A=<(1,2:3,4); add(=<A[0]=>,=<A[1]=>) -> (4,6) clear; add(=<A,=<B)=<A=>+B=>; A=(1,2:3,4); add(=<A[0],=<A[1]) -> (4,6) ・定義元とcall先のscopeを区別する場合 clear; add(A,B)=<[A+B]; A=(1,2:3,4); add(=<A[0],=<A[1]) -> (4,6) clear; add(A,B)=<[A+B]; A=<(1,2:3,4); add(=<A[0],=<A[1]) -> (4,6) clear; add(=<A,=<B)=<[A=>+B=>]; A=(1,2:3,4); add(=<A[0],=<A[1]) -> (4,6) clear; add(=<A_,=<B_)=<[A_=>+B_=>]; A=<(1,2:3,4); add(=<A[0],=<A[1]) -> (4,6) Ver.2.33.18以降、定義元argumentsの式変数は宣言時の階層に依存する ・Ver.2.219.50以降、式渡し記号=<の仕様を変更(元scopeを維持) ・通常callの場合 clear; conv(=<a_)=<last(a_=>),[a=3,conv(=<a)=>] -> [MyErr]Undef eqn(a) clear; conv(=<a_)=<last(a_=>),[a=3,a=<a,conv(=<a)=>] -> clear; conv(=<a_)=<last(a_=>),[a=3,conv(=<(a))=>] -> clear; [conv(=<a_)=<last(a_=>),[a=3,conv(=<(a))=>]] -> ・定義元で宣言される変数・式変数は定義元scopeに定義する clear; conv(=<a_)=<last(a=-3,a_=>),[a=3,a=<a,conv(=<a)=>,a],a -> (0,0,0, clear; conv(=<a_)=<last(a=-3,a_=>),[a=3,conv(=<(a))=>,a],a -> (0,0, clear; [conv(=<a_)=<last(a=-3,a_=>),[a=3,conv(=<(a))=>,a],a] -> (0,0, clear; [conv(=<a_)=<last(a=-3,a_=>),[a=3,conv(=<(a))=>,a],a],a -> [MyErr]Invalid REv(a) ・式変数のscope継承callの場合 clear; conv(=<a_)=<last(a_=>),[a=3,a=<a,conv(=<a)==>,a] -> (0,0,0,3,3) clear; conv(=<a_)=<last(a_=>),[a=3,conv(=<(a))==>,a] -> (0,0,3,3) clear; [conv(=<a_)=<last(a_=>),[a=3,conv(=<(a))==>,a]] -> (0,0,3,3) ・定義元で宣言される変数・式変数はcall先scopeに定義する clear; conv(=<a_)=<last(a=-3,a_=>),[a=3,a=<a,conv(=<a)==>,a] -> (0,0,0,-3,-3) clear; conv(=<a_)=<last(a=-3,a_=>),[a=3,conv(=<(a))==>,a] -> (0,0,-3,-3) clear; [conv(=<a_)=<last(a=-3,a_=>),[a=3,conv(=<(a))==>,a]] -> (0,0,-3,-3) clear; [conv(=<a_)=<last(a=-3,a_=>),[a=3,conv(=<(a))==>,a],a] -> [MyErr]Invalid REv(a) clear; [conv(=<a_)=<last(b=4,a_=>),[a=3,conv(=<(a))==>,b],b] -> [MyErr]Invalid REv(b) clear; [conv(=<a_)=<last(b=4,a_=>),[a=3,conv(=<(a))==>,a,b]] -> (0,0,3,3,4) ・定義元とcall先のscopeを区別する場合 ・定義元で宣言される変数・式変数はcall先から参照不可 clear; [conv(=<a_)=<last[b=4,a_=>],[a=3,conv(=<(a))==>,b]] -> [MyErr]Invalid REv(b) clear; [conv(=<a_)=<last[b=<4,a_=>],[a=3,conv(=<(a))==>,b=>]] -> [MyErr]Invalid REv(b) clear; [conv(=<a_)=<last[b=4,a_=>+b],[a=3,conv(=<(a))==>]] -> (0,0,7) clear; [conv(=<a_)=<last[b=<4,a_=>+b=>],[a=3,conv(=<(a))==>]] -> (0,0,7) ・symbol渡しで定義元scopeを継承する場合 clear; conv(=<a_)=<(a=-1,=<a+a_=>)=>*2; a=<a; a=1; conv(=<a)=>,a -> (-4,-1) clear; conv(=<a_)=<[a=-1,=<a+a_=>]=>*2; a=<a; a=1; conv(=<a)=>,a -> (0,1) clear; conv(=<a_)=<[a=-1,=<a+a_==>]=>*2; a=<a; a=1; conv(=<a)=>,a -> (-4,1) ・symbol渡しを式変数のscope継承callで代替する場合、nestingが必要 clear; conv(=<a_)=<[=<a+a_=>]=>*2; a=<-a; a=1; conv(=<a)=>,a -> (0,1) clear; conv(=<a_)=<[=<a+a_=>]=>*2; a=<a; a=1; conv(=<(a=>))=>,a -> (4,1) clear; conv(=<a_)=<[a=-1,=<a+a_=>]=>*2; a=<a; a=1; conv(=<(a=>))=>,a -> (0,1) clear; conv(=<a_)=<[a=-1,=<a+a_=>]=>*2; a=<a; a=1; conv(=<(a==>))=>,a -> (0,1) clear; conv(=<a_)=<[a=-1,=<a+a_==>]=>*2; a=<a; a=1; conv(=<(a=>))=>,a -> (0,1) clear; conv(=<a_)=<[a=-1,=<a+a_==>]=>*2; a=<a; a=1; conv(=<(a==>))=>,a -> (-4,1) ・単独scopeの場合 clear; conv(=<a_)=<[a=-1,=<a+a_==>]=>; a=<a; a=1; conv(=<a)=>,a -> (-2,1) clear; conv(=<a_)=<[a=-1,=<a+a_==>]=>; a=<a; a=1; conv(=<(a))=>,a -> (-2,1) clear; conv(=<a_)=<[a=-1,=<a+a_==>]=>; a=<a; a=1; conv(=<(a==>))=>,a -> (-2,1) clear; conv(==<a_)=<[a=-1,=<a+a_=>]=>; a=<a; a=1; conv(=<a)=>,a -> (-2,1) clear; conv(==<a_)=<[a=-1,=<a+a_=>]=>; a=<a; a=1; conv(=<(a==>))=>,a -> (-2,1) clear; conv(==<a_)=<[a=-1,=<a+a_=>]=>; a=<a; a=1; conv(=<(a=>))=>,a -> (0,1) clear; conv(=<a_)=<[a=-1,=<a+a_=>]=>; a=<a; a=1; conv(=<(a==>))=>,a -> clear; conv(=<a_)=<[a=-1,=<a+a_==>]=>; a=<a; a=1; conv(=<(a=>))=>,a -> (0,1) clear; conv(=<a_)=<[a=-1,=<a+a_=>]=>; a=<a; a=1; conv(=<(a=>))=>,a -> (0,1) |
|
目次
arguments 入力仕様 |
式変数のargumentsの入力仕様と付随する留意事項について記述する
式変数のargumentsは次の関数定義と関数callを代替する let add=(a,b)=>a+b; add(1,2) // ES6 -> 3 clear; add(a,b)=<a+b; add(1,2)=> || add(1,2) -> 3 ・以降、式変数の定義元に対してcall先と区別する ・Ver.2.791.126以降、symbol渡し||name渡しの重複宣言を禁止 clear; f(x,x)=<1 -> [MyErr]Invalid duplicate-args.x(f) clear; f(x,=<x)=<1 -> [MyErr]Invalid duplicate-args.x(f) clear; f(x,==<x)=<1 -> [MyErr]Invalid duplicate-args.x(f) clear; f(x,?x)=<1 -> [MyErr]Invalid duplicate-args.x(f) clear; f(x,$x)=<1 -> [MyErr]Invalid duplicate-args.x(f) clear; ((1,2,3).map((x,j,j)=<j)) -> [MyErr]Invalid duplicate-args.j(null) ・Ver.2.823.135以降、式変数のargumentsの直列化に対応 m2x2=(1,2:3,4),ab=[1,###m2x2],f(a,b:c,d)=<(a,b,c,d),g(a,=<b:$c,?d)=<(a,b,c,d); g(1,=<2,$ab,?f) -> (1,eqn,1,4,eqn(a,b,c,d)) f(m2x2):f(reshape(m2x2:ab)):f(reshaper(m2x2:ab)):f(reshapec(m2x2:ab)) -> (1,2,3,4:1,2,3,4:1,2,3,4:1,3,2,4) 行列の値渡しの場合、式渡しを使用 clear; add(A,B)=<A+B; add((1,2:3,4),(5,6:7,8)) -> [MyErr]Invalid args.length=2(add) clear; add(A,B)=<A+B; add(=<(1,2:3,4),=<(5,6:7,8))=> -> (6,8:10,12) clear; add(A,B)=<A+B; add(=<(1,2:3,4),=<(5,6:7,8)) -> (6,8:10,12) 変数・式変数の式渡しの場合 clear; add(=<A_,=<B_)=<A_+B_; A=<(1,2:3,4); B=<(5,6:7,8); add(=<A=>,=<B=>)=> -> (6,8:10,12) clear; add(=<A_,=<B_)=<A_+B_; A=<(1,2:3,4); B=<(5,6:7,8); add(=<A=>+A=>,=<B=>+B=>)=> -> (12,16:20,24) clear; add(=<A_,=<B_)=<A_+B_; A=<(1,2:3,4); B=<(5,6:7,8); add(=<{A=>+A=>},=<(B=>+B=>))=> -> (12,16:20,24) clear; add(=<A_,=<B_)=<A_+B_; A=<(1,2:3,4); B=<(5,6:7,8); add(=<[A=>+A=>],=<[B=>+B=>])=> -> (12,16:20,24) 定義元argumentsの式変数名symbolをunderscoreでescapeする理由を列挙する ・symbol渡しで式変数Bの中身をcallする場合、問題なし clear; add(A,=<B)=<A+B=>; B=<(3,4); add(=<(1,2),=<B) -> (4,6) ・定義元から式変数Bをcallする場合、式変数名symbolの循環参照(B=>B=>)と判別される clear; add(A,=<B)=<A+B=>; B=<(3,4); add(=<(1,2),=<B=>) -> Maximum call stack size exceeded ・参照上の問題はないため、定義元argumentsの式変数名symbolをescapeする clear; add(A,=<B_)=<A+B_=>; B=<(3,4); add(=<(1,2),=<B=>) -> (4,6) clear; add(A,=<B_)=<A+B_=>; B=<(3,4); add(=<(1,2),=<B) -> (4,6) ・以降、escape文字は後置のunderscoreで統一する clear; add(A,=<B_)=<(A+B_=>); B=<(3,4); add(=<(1,2),=<B=>) -> (4,6) clear; add(A,=<B_)=<(A+B_=>); B=<(3,4); add(=<(1,2),=<B) -> (4,6) clear; add(A,=<B_)=<[A+B_=>]; B=<(3,4); add(=<(1,2),=<B=>) -> (4,6) clear; add(A,=<B_)=<[A+B_=>]; B=<(3,4); add(=<(1,2),=<B) -> (4,6) ・定義元argumentsが式渡しの場合、式変数名symbolのみ判別する clear; add(A,=<B_)=<[A+B_=>]; B=<(3,4); B=(,); add(=<(1,2),=<B) -> (4,6) ・定義元argumentsが値渡しの場合、変数名symbolを優先する clear; add(A,B)=<[A+B]; B=<(3,4); add(=<(1,2),=<B) -> (4,6) clear; add(A,B)=<[A+B]; B=<(3,4); B=(,); add(=<(1,2),=<B) -> (1,2) clear; add(A,B)=<[A+B]; B=<(3,4); B=(,); add(=<(1,2),=<B=>) -> (4,6) ・strict-modeの場合、変数名symbolを厳格に判別する clear; add(A,B)=<[A+B]; B=<(3,4); add(=<(1,2),=<B)=> -> [MyErr]Invalid BRsa operation clear; add(A,B)=<[A]; B=<(3,4); add(=<(1,2),=<B)=> -> (1,2) clear; add(A,B)=<[B]; B=<(3,4); add(=<(1,2),=<B)=> -> [MyErr]Invalid REv(B) clear; add(A,B)=<[A+B]; B=<(3,4); B=(,); add(=<(1,2),=<B)=> -> (1,2) clear; add(A,B)=<[A+B]; B=<(3,4); B=(,); add(=<(1,2),=<B=>)=> -> (4,6) clear; add(A,=<B_)=<(A+B_=>); B=<(3,4); add(=<(1,2),=<B=>)=> -> (4,6) clear; add(A,=<B_)=<(A+B_=>); B=<(3,4); add(=<(1,2),=<B)=> -> (4,6) clear; add(A,=<B_)=<[A+B_=>]; B=<(3,4); add(=<(1,2),=<B=>)=> -> (4,6) clear; add(A,=<B_)=<[A+B_=>]; B=<(3,4); add(=<(1,2),=<B)=> -> (4,6) 式渡しの場合、symbol渡しと異なり、定義元scopeに留意が必要 ・次の場合、B=>を定義元の式変数B_に継承する clear; add(A,=<B_)=<(a=-1,=<A+B_=>)=>; B=<(a,4); a=1; add(=<(1,2),=<B=>)=> -> (0,6) clear; add(A,=<B_)=<(a=-1,=<A+B_=>)=>; B=<(a,4); a=1; add(=<(1,2),=<[B=>])=> -> (0,6) ・以上の場合、定義元scopeとlocal storageが共通で式変数Bをcallする clear; add(A,=<B_)=<[a=-1,=<A+B_=>]=>; B=<(a,4); a=1; add(=<(1,2),=<B=>)=> -> (2,6) clear; add(A,=<B_)=<[a=-1,=<A+B_=>]=>; B=<(a,4); a=1; add(=<(1,2),=<[B=>])=> -> (2,6) ・以上の場合、定義元scopeから参照可能なlocal storageに定義された式変数Bをcallする ・よって定義元scopeを式変数Bに継承する場合、式変数のscope継承callをnestingする clear; add(A,=<B_)=<[a=-1,=<A+B_==>]=>; B=<(a,4); a=1; add(=<(1,2),=<(B==>))=> -> (0,6) ・独立scopeに式変数Bが定義された場合、定義元scopeから参照不可 clear; add(A,=<B_)=<[a=-1,=<A+B_=>]=>; [B=<(a,4),a=1,add(=<(1,2),=<B=>)=>] -> [MyErr]Invalid REv(B) 式変数のscope継承callを代替する一例を次に示す clear; a=<b+c+d; d=3; [c=2,=<[b=1,=<a==>]=>]=> -> 6 clear; a()=<b+c+d; d=3; [c=2,=<[b=1,=<a()==>]=>]=> -> 6 clear; a(b,c,d)=<b+c+d; d=3; [c=2,=<[b=1,=<a(b,c,d)]=>]=> // better -> 6 clear; a(b,c,d)=<b+c+d; d=3; [c=2,=<[b=1,=<a(b,c,d)=>]=>]=> // better -> 6 ・定義元argumentsの変数名symbolは独立としてstatic scopes2d arrayを共有する clear; a(b,c,d)=<last{b=-1,b+c+d}; d=3; [c=2,=<[b=1,=<[a(b,c,d),b]]=>]=> -> (4,1) clear; a(b,c,d)=<last{b=-1,b+c+d}; d=3; [c=2,=<[=<[a(b,c,d),b]]=>]=> -> [MyErr]Invalid REv(b) ・通常callの場合、定義元で宣言される変数・式変数は定義元scopeに定義する clear; a(b_,c,d)=<last{b=b_,b_+c+d}; d=3; [c=2,=<[=<[a(1,c,d),b]]=>]=>,b -> (6,1,1) clear; a(b_,c,d)=<last{b=<1,b_+c+d}; d=3; [c=2,=<[=<[a(1,c,d),b=>]]=>]=>,b=> -> (6,1,1) clear; a(b_,c,d)=<last{b=b_,b_+c+d}; d=3; [c=2,=<[=<[a(1,c,d),b_]]=>]=> -> [MyErr]Invalid REv(b_) test caseを列挙する clear; add(a,b)=<last{a=-1,a+b}; add(last{a=1,a},2)=>,a -> (1,1) clear; add(a_,b)=<last{a=-1,a_+b}; add(last{a=1,a},2)=>,a -> (3,-1) clear; add(a_,b)=<last{a=-1,a_+b}; add(last{a=1,a},2)=>,a_ -> [MyErr]Invalid REv(a_) Ver.2.32.17以降、scope付式変数の再利用に対応 clear; add(a_,b)=<last[a=-1,a_+b]; add(last{a=1,a},2)=>,a -> (3,1) clear; add(a_,b)=<last[a=-1,a_+b]; add(last[a=1,a],2)=>,a -> [MyErr]Invalid REv(a) clear; add(a_,b)=<last(a=-1,a_+b); add(last[a=1,a],2)=>,a -> (3,-1) clear; conv(=<a)=<last{a=<-1,a=>}; conv(=<last{a=<1,a=>})=> -> -1 clear; conv(=<a)=<last{a=<-1,a=>}; conv(=<last{a=<1,a=>})=>; a=> -> [MyErr]Invalid REv(a) clear; conv(=<a_)=<last{a=<-1,a_=>}; conv(=<last{a=<1,a=>})=>,a=> -> (1,1) clear; conv(=<a_)=<last{a=<-1,a_=>}; conv(=<last{a=>})=>,a=> -> (-1,-1) clear; conv(=<a_)=<last[a=<-1,a_=>]; conv(=<last{a=>})=> -> -1 clear; conv(=<a_)=<last[a=<-1,a_==>]; conv(=<last{a=>})=> -> -1 clear; conv(=<a_)=<last[a=<-1,a_=>]*2; conv(=<last{a=>})=> -> [MyErr]Invalid REv(a) clear; conv(=<a_)=<last[a=<-1,a_==>]*2; conv(=<last{a=>})=> -> -2 clear; conv(=<a_)=<last[a=<-1,a_==>]; conv(=<last[a=>])=> -> [MyErr]Invalid FNm(last) clear; conv(=<a_)=<last[a=<-1,a_==>]; conv(=<last[,a=>])=> -> -1 clear; conv(=<a_)=<last[a=<-1,a_=>]; conv(=<last[,a=>])=> -> -1 clear; conv(=<a_)=<last[a=<-1,a_=>]; conv(=<last[a=<1,a=>])=> -> 1 clear; conv(=<a_)=<last[a=<-1,a_=>]*2; conv(=<last[,a=>])=> -> [MyErr]Invalid REv(a) clear; conv(=<a_)=<last[a=<-1,a_==>]*2; conv(=<last[,a=>])=> -> -2 clear; conv(=<a_)=<last[a=<-1,a_=>]*2; conv(=<last[a=<1,a=>])=> -> 2 Ver.2.32.17以降、式読出し記号=>省略時同様に clear; add(A,B)=<A+B; add[0](=<(1,2:3,4),=<(5,6:7,8)) || (6,8:10,12)[0] -> (6,8) ・角括弧[]で式変数の返値の行列要素を参照可 clear; add(A,B)=<A+B; add[0](=<(1,2:3,4),=<(5,6:7,8))=> -> (6,8) clear; add(A,B)=<A+B; add[1](=<(1,2:3,4),=<(5,6:7,8))=> -> (10,12) clear; add(A,B)=<A+B; add[0][0](=<(1,2:3,4),=<(5,6:7,8))=> -> 6 clear; add(A,B)=<A+B; add[1][1](=<(1,2:3,4),=<(5,6:7,8))=> -> 12 Ver.2.174.42以降、Non-strict-modeのみ、call先argumentsを省略可 ・Ver.2.253.59以降、call先argumentsを省略不可 clear; f(x)=<2*x+1,x=0,f(x),f=>,f==>:[,x=1,f(x),f=>,f==>:[,x=2,f(x),f=>,f==>]] -> 0,0,1,1,1: 0,0,3,1,3: 0,0,5,1,5 ) clear; x(t)=<-t; f=<x+1; f -> [MyErr]Invalid null args(x) clear; x(t)=<-t; f=<x=>+1; f -> [MyErr]Invalid binary operation clear; x(t)=<-t; t=-999; f=<x=>+1; f -> 1000 clear; x(t)=<-t; t=-999; [t=1,f=<x=>+1,f] -> (0,0,1000) clear; x(t)=<-t; t=-999; [t=1,f=<x==>+1,f] -> (0,0,0) clear; x(t)=<-t; t=-999; [t=1,f=<x(t)==>+1,f] -> (0,0,0) clear; x(t)=<-t; t=-999; [t=1,f=<x(t)=>+1,f] -> (0,0,0) clear; x(t)=<-t; t=-999; [t=1,f=<x(t)+1,f] -> (0,0,0) clear; x=<-t; t=-999; [t=1,f=<x+1,f] -> (0,0,1000) clear; x=<-t; t=-999; [t=1,f=<x=>+1,f] -> (0,0,1000) clear; x=<-t; t=-999; [t=1,f=<x==>+1,f] -> (0,0,0) arguments不正の場合、error終了 ・定義元argumentsに関数を指定した場合、変数名symbolとは判別されない clear; a(max)=<max*2; a()=> || max*2 -> [MyErr]Invalid binary operation clear; a(max)=<2; a()=> || a()=<2; a()=> || a=<2; a=> -> 2 ・Ver.2.252.59以降、式変数のargumentsのerror処理を修正 clear; a(max)=<max*2; a(2)=> -> [MyErr]Invalid args isFound(a) clear; f(3,x)=<x; f(3,3)=> -> [MyErr]Invalid args.length=0(f) clear; f(3,x)=<x -> [MyErr]Invalid args isFound(f) ・argumentsの変数名symbolは変数の命名規則に準拠 ・Ver.2.249.57以降、再代入と重複宣言を禁止するconst宣言を暫定追加($開始のbeta版) |
|
目次
symbol渡し 入力仕様 |
式変数のsymbol渡しの入力仕様と付随する留意事項について記述する
変数名symbolを式渡しする場合、symbol渡しと定義する ・Ver.2.251.58以降、symbol渡しの判定を修正 clear; a=3,f(=<g)=<g(a)=>,f((x)=<x)=> -> clear; a=3,f(=<g)=<g(a)=>,f((x)=<x+1)=> -> (0,0,4) clear; a=3,f((args)=<g)=<g(a)=>,f((x)=<x+1)=> -> ・Ver.2.833.140以降、symbol渡しの自動展開:なし ⇒ あり clear; f(x)=<d=x:[($a)=(=<f/*Non-strict-mode*/),b=(=<f),c=[],c.push(=<f),[a,b,c]] -> clear; c=[],c.push(=<f) -> [MyErr]Undef eqn(f) ・変数を使用 clear; add(A,B)=<A+B; A=(1,2:3,4); B=(5,6:7,8); add(A,B)=> -> [MyErr]Invalid args.length=2(add) clear; add(A,B)=<A+B; A=(1,2:3,4); B=(5,6:7,8); add(=<A,=<B)=> || add(=<A,=<B) -> (6,8:10,12) ・式変数を使用 clear; add(A,B)=<A+B; A=<(1,2:3,4); B=<(5,6:7,8); add(=<A,=<B)=> -> (6,8:10,12) clear; add(=<A_,=<B_)=<A_=>+B_=>; A=<(1,2:3,4); B=<(5,6:7,8); add(=<A,=<B)=> -> (6,8:10,12) clear; add(=<A_,=<B_)=<A_+B_; A=<(1,2:3,4); B=<(5,6:7,8); add(=<A,=<B)=> -> (6,8:10,12) ・call先argumentsは最終行vectorの左から順に参照(高階関数同様に、拡張機能なし) add(1,2:3,4) || add(3,4) -> 7 add(=<A,=<A:=<B,=<B)=> || add(=<B,=<B) -> (10,12:14,16) ・引数の要素を指定する場合、引数の右側に行列indexを追加する add(1,2:3,4)[0] || add((1,2:3,4)[0]) || add(1,2) -> 3 add(=<A,=<A:=<B,=<B)[0]=> || add((=<A,=<A:=<B,=<B)[0])=> || add(=<A,=<A)=> -> (2,4:6,8) ・引数の要素数が異なる場合、error終了(関数の引数と異なり、厳格に判別する) add(1,2:3,4)[0][0] -> [MyErr]Invalid args.length=2(add) add(=<A,=<A:=<B,=<B)[0][0]=> -> [MyErr]Invalid args.length=2(add) add(=<A,=<A,=<A)=> -> [MyErr]Invalid args.length=2(add) ・返値の要素を指定する場合、式変数名の右側に行列indexを追加する add[0](1,2:3,4)[0] -> 3 add[1](=<A,=<A:=<B,=<B)[0]=> -> (6,8) add[1][1](=<A,=<A:=<B,=<B)[0]=> -> 8 symbol渡しの場合、定義元scopeに留意が不要(別scopeを参照するcaseを除く) ・次の場合、式変数Bの中身(a,4)を定義元の式変数B_に継承する clear; add(A,=<B_)=<(a=-1,=<A+B_=>)=>; B=<(a,4); a=1; add(=<(1,2),=<B)=> -> (0,6) clear; add(A,=<B_)=<(a=-1,=<A+B_=>)=>; a=1; add(=<(1,2),=<(a,4))=> -> (0,6) clear; add(A,=<B_)=<[a=-1,=<A+B_=>]=>; B=<(a,4); a=1; add(=<(1,2),=<B)=> -> (0,6) clear; add(A,=<B_)=<[a=-1,=<A+B_=>]=>; a=1; add(=<(1,2),=<(a,4))=> -> (0,6) clear; add(A,=<B_)=<[a=-1,=<A+B_=>]=>; a=1; add(=<(1,2),=<{=<(a,4)}=>)=> -> (0,6) clear; add(A,=<B_)=<[a=-1,=<A+B_=>]=>; a=1; add(=<(1,2),=<{=<(a,4)}=>)=> -> (0,6) ・変数名symbolを括弧で括った場合、式渡しと判別される clear; add(A,=<B_)=<[a=-1,=<A+B_=>]=>; B=<(a,4); a=1; add(=<(1,2),=<(B))=> -> (2,6) ・高階関数のsymbolのみを渡す引数と異なる |
|
目次
name渡し 入力仕様 |
name渡しの入力仕様と付随する留意事項について記述する
Ver.2.246.57以降、式変数のargumentsのname渡しに対応 ・Ver.2.791.125以降、予期せぬerror終了を修正 x=1; f(y)=<y; f($x) -> x=1; f($y)=<y; f($x) -> 1 |
|
目次
scope付 式変数の 再利用 入力仕様 |
scope付式変数の再利用の入力仕様と付随する留意事項について記述する
再利用の一例を以下に示す clear; add(a,b)=<last[,a+b]; add(1,3) -> 4 add(1,-3),add(1,i) -> (-2,1+i) ・値を返す場合、nesting可 add(1,add(1,add(1,add(1,i)))) -> 4+i add(1,add(2,add(3,add(4,i)))) -> 10+i add(1,add(1,add(1,add(1,i))add(1,i))add(1,i))add(1,i) -> -5+5i ・同義 (1+(1+(1+(1+i)))) -> 4+i (1+(2+(3+(4+i)))) -> 10+i (1+(1+(1+(1+i))(1+i))(1+i))(1+i) -> -5+5i last行列関数を代替する式変数last_ttを以下に示す ・last行列関数は単位tree構造の仕様上、行vectorの欠損要素を自動で埋めない ・行vectorの欠損要素を自動で埋める式変数last_ttを次に定義する clear; last_tt(A)=<(trans(trans(A)))[sizer(A)-1][sizec(A)-1]; A=(1,2:3,4); last_tt(=<A) -> 4 ・行列要素参照の角括弧[]も同様に、scopeを持つ A=(1,2:3,(,:,4),5); last(A) -> 4 A=(1,2:3,(,:,4),5); last(trans(trans(A))) -> 0 A=(1,2:3,last(,:,4),5); last(A) -> 5 A=(1,2:3,(,:,4),5); last_tt(=<A) -> 0 A=(1,2:3,last_tt(=<(,:,4)),5); last_tt(=<A) -> 5 A4=(,:,4); A=(1,2:3,last_tt(=<A4),5); last_tt(=<A) -> 5 ・Ver.2.156.38以降、irregular行列の行列結合の仕様変更 A4=(,:,4); A=(1,2:3,A4,5) -> ( 1,2: 3,0,0,5: ) ttA=trans(trans(A)) -> ( 1,2,0,0: 3,0,0,5: ) sizer(A)-sizer(ttA),sizer(A) -> (0,3) sizec(A)-sizec(ttA),sizec(A) -> (0,4) ・Ver.2.185.44以降、size行列関数の非正方行列の返値の仕様変更 size(A) -> (3:4) 留意事項を列挙する ・scope変数は演算実行確定1回毎に初期化のため、式変数への式読出しで再利用不可 ・static scopes2d arrayを共有するため、同じ変数名symbolの代入不可(前回callの未初期化dataが残存) scope_NG1(x)=<[x=x,x,last[x=x/*NG*/,x],x]; ・Ver.2.210.46以降、単独scopeの判定を厳格化(scope_NGのNG範囲を最小化) clear; scope_NG1(x)=<[x=x,x,last[x=x/*NG*/,x],x]; scope_NG2(x)=<2*[x=x,x,last[x=x/*NG*/,x],x]; scope_NG3(x)=<last[,3]*[x=x,x,last[x=x/*NG*/,x],x]; scope_NG4(x)=<last[x=4,x]*[x=x/*NG*/,x,last[x=x/*NG*/,x],x]; check_all(x)=<(scope_NG1(x)=>:scope_NG2(x)=>:scope_NG3(x)=>:scope_NG4(x)=>); store; scope_NG1(1)=>:scope_NG1(-1)=> -> (0,1,1,1:0,-1,1,-1) scope_NG2(1)=>:scope_NG2(-1)=> -> (0,2,2,2:0,-2,2,-2) scope_NG3(1)=>:scope_NG3(-1)=> -> (0,3,3,3:0,-3,3,-3) scope_NG4(1)=>:scope_NG4(-1)=> -> (0,4,4,4:0,4,4,4) ・命令文を使用 restore; check_all(1)=> -> (0,1,1,1:0,2,2,2:0,3,3,3:0,4,4,4) check_all(-1)=> -> (0,-1,1,-1:0,-2,2,-2:0,-3,3,-3:0,4,4,4) restore; check_all(1)=> -> (0,1,1,1:0,2,2,2:0,3,3,3:0,4,4,4) restore; check_all(-1)=> -> (0,-1,-1,-1:0,-2,-2,-2:0,-3,-3,-3:0,-4,-4,-4) |
|
目次
再帰call |
式変数のargumentsの再帰callの入力仕様と付随する留意事項について記述する
Ver.2.194.45以降、式変数のargumentsの再帰callに対応 ・Ver.2.195.46以降、訂正 test caseを列挙する ・Fibonacci数列 N=10; F0=0,F1=1,F2=<last{F2=F0+F1,F0=F1,F1=F2,F2}; ・再帰高階関数を使用 Fibonacci(n)=<_rn(=<F2,,n-1); Fibonacci(N) -> 55 ・指数時間の再帰call N=10; fibo_exp(n)=<(n<2&&&{n,}|||{fibo_exp(n-1)+fibo_exp(n-2),})[0]; fibo_exp(N) -> 55 ・線形時間の再帰call N=10; fibo_(n,a,b)=<(n<1&&&{a,}|||n<2&&&{b,}|||{fibo_(n-1,b,a+b),})[0]; fibo_(N,0,1) -> 55 ・対数時間の再帰call(単独scopeと短絡評価に留意) N=10; fibo_log(n)=<[=<n<2&&n||||last{q=n%%2,fq=fibo_log(q), fq**2+(n%2===0&&&2fibo_log(q-1)*fq||||fibo_log(q+1)**2)}]=>; fibo_log(N) -> 55 ・一般項(再帰なし) N=10; fibo(n)=<last{sqrt5=sqrt(5),round((((1+sqrt5)/2)**n-((1-sqrt5)/2)**n)/sqrt5)}; fibo(N) -> 55 ・行列演算 N=10; fibo(n)=<first(_p((n)=<(1,1:1,0),,n-2)); fibo(N) -> 55 ・Ver.2.196.46以降、条件演算子代替の論理演算子(literal)を追加 N=10; fibo_exp(n)=<n<2&&&&n||||fibo_exp(n-1)+fibo_exp(n-2); fibo_exp(N) -> 55 N=10; fibo_(n,a,b)=<n<1&&&&a||||n<2&&&&b||||fibo_(n-1,b,a+b); fibo_(N,0,1) -> 55 ・Ver.2.196.46以降、可読性の最適化 N=10; fibo_exp(n)=<n<2&&n||||fibo_exp(n-1)+fibo_exp(n-2); fibo_exp(N) -> 55 N=10; fibo_(n,a,b)=<n<1&&a||||n<2&&b||||fibo_(n-1,b,a+b); fibo_(N,0,1) -> 55 ・以上より、先行するk項の和で一般化 fibok(n,k)=<n<k-1&&0||||n<k&&1||||_sm(=<fibok(n-m,k)=>,1,k); fibok(n,k)=<n<k-1&&0||||n<k|||_sm(=<fibok(n-m,k)=>,1,k); fibok(10,2) -> 55 fibok(10,3) -> 81 fibok(10,4) -> 56 fibok(10,5) -> 31 ・単純な階乗 N=10; fact_(n)=<n<=1&&&1|||round(n)*fact_(n-1); fact_(N) -> 3628800 N=10; fact_(n)=<n<=1|||round(n)*fact_(n-1); fact_(N) -> 3628800 N=10; fact_(n)=<n<=1|||n*fact_(n-1); fact_(N) -> 3628800 ・厳密な階乗 N=10; fact_(n)=<(isNaN(n)&&&{NaN,}|||n<1&&&{false,}|||round(n)===1&&&{1,}|||{round(n)*fact_(n-1),})[0]; fact_(N) -> 3628800 ・総和 N=10; fn=<(n,n*(1+i)); sum_(n)=<n>0&&&fn+sum_(n-1); sum_(N) -> (55,55+55i) N=10; fn(n)=<(n,n*(1+i)); sum_(n)=<n>0&&&fn(n)+sum_(n-1); sum_(N) -> (55,55+55i) ・総積 N=10; prod_(n,A)=<n<1&&&1|||A*prod_(n-1,=<A); prod_(N,=<(1,2:3,4)) -> (4783807,6972050:10458075,15241882) N=10; prod_(n,A)=<n<1|||A*prod_(n-1,=<A); prod_(N,=<(1,2:3,4)) -> (4783807,6972050:10458075,15241882) ・Seki-AitkenのΔ2乗加速法 tn(=<sn,n)=<last[,sn(n)-(sn(n+1)-sn(n))**2/(sn(n+2)-2sn(n+1)+sn(n))]; sn(n)=<sin(pi/2**n)*2**n; n=0; sn(n) -> 1.2246467991473532e-16 n=8; sn(n) -> 3.141513801144301 n=17; sn(n) -> 3.141592653288993 n=27; sn(n) -> 3.1415926535897927 n=28; sn(n) -> 3.141592653589793 pi -> 3.141592653589793 n=0; tn(=<sn,n) -> infoLost[r ] 3.414213562373094 n=8; tn(=<sn,n) -> 3.141592653626903 n=15; tn(=<sn,n) -> 3.1415926535897936 ・指数時間の多重化 n=0; tn((n)=<tn(=<sn,n),n) -> infoLost[r ] 3.141796445191483 n=0; tn((n)=<tn((n)=<tn(=<sn,n),n),n) -> infoLost[r ] 3.1415926587564154 n=0; tn((n)=<tn((n)=<tn((n)=<tn(=<sn,n),n),n),n) -> infoLost[r ] 3.1415926535897927 留意事項を列挙する ・RA選択の場合、要修正 N=10; fact_(n)=<n<=1|||round(n)*fact_(n-1); fact_(N) -> Maximum call stack size exceeded ・無限loopの場合、error終了 N=10; fact_=<round(n)*fact_; fact_ -> Maximum call stack size exceeded N=10; fact_(n)=<round(n)*fact_(n-1); fact_(N) -> Maximum call stack size exceeded |
|
目次
無名call |
式変数のargumentsの無名callの入力仕様と付随する留意事項について記述する
Ver.2.195.45以降、式変数のargumentsの無名call(式渡しの直接式読出しのarguments)に対応 ・Ver.2.195.46以降、実行確定の都度、local storageから削除(closure外の0階層のみ、実行文毎に削除) ・Ver.2.204.46以降、call結果が解決済みの前提(Ver.2.211.46以降、式変数への式読出しを除く) test caseを列挙する ・式渡しの直接式読出し(Ver.2.195.45以降、無名callのarguments省略) [=<0]=> -> 0 [()=<1]()=> -> 1 ・式渡しの直接式読出しにargumentsを追加 [(x)=<x](2)=> -> 2 [(a,b)=<(a,b)](3,=<(i,2i))=> -> (3,i,2i) ・(function(x,y){var a=1; var b=2; return a*x+b*y;})(1,2); [(x,y)=<[a=1,b=2,=<a*x+b*y]=>](1,2)=> -> 5 [(x,y)=<[a=1,b=2,fxy=<a*x+b*y,=<fxy=>]=>](1,2)=> -> 5 [(x,y)=<[a=1,b=2,fxy(c,d)=<c*x+d*y,=<fxy(a,b)=>]=>](1,2)=> -> 5 ・(function(a){return (function(b){return (function(c){return a+b+c;})(3);})(2);})(1); [(a)=<[(b)=<[(c)=<a+b+c](3)=>](2)=>](1)=> -> 6 [(a)=<[(b)=<[(c)=<[d=a+b+c,=<d]=>](3)=>](2)=>](1)=> -> 6 ・scopeの挙動 [(a)=<[(b)=<[[a=4,b=5],(c)=<a+b+c=1+2+3](3)=>](2)=>](1)=> -> 0 [(a)=<[(b)=<[a=4,b=[a=5,=<a]=>,(c)=<a+b+c=4+5+3](3)=>](2)=>](1)=> -> 0 [(a)=<[(b)=<[(c)=<[[a=4,b=5],=<a+b+c=1+2+3]=>](3)=>](2)=>](1)=> -> 0 [(a)=<[(b)=<[(c)=<[a=4,b=[a=5,=<a]=>,=<a+b+c=4+5+3]=>](3)=>](2)=>](1)=> -> 0 ・式渡し clear; f(n)=<n<=1|||round(n)*f(n-1); [n=10,(=<fn)=<fn=>](=<f)=> -> 3628800 ・strict-mode clear; f(n)=<n<=1|||round(n)*f(n-1)=>; [n=10,(=<f)=<f(n)=>](=<f)=> -> 3628800 ・無名再帰(名前付きlambda式に相当) ([fact_=(n)=<n<=1|||n*fact_(n-1),=<fact_]=>)(10)=> -> 3628800 留意事項を列挙する ・複数列挙の場合、末尾returnのみ取り出す(途中return不可) [a=1,(b)=<a=2,(b)=<a=3,(b)=<a+b](10)=> || [a=1,(b)=<a+b](10)=> -> 11 clear; d=<-a*z+b*A+c; [a=1,(z,A)=<[b=2,(c)=<d==>](a*z)=>](i,=<(1,2:3,4))=> -> (2,4:6,8) ・call記号=>省略不可 [(x)=<x](2) -> [MyErr]Invalid FN operation [(x)=<x](2)=> -> 2 ・返値の要素を指定する場合、括弧を明示 clear; f(x)=<(1,2:3,x); f[1](5) -> (3,5) ([(x)=<(1,2:3,x)](5)=>)[1] -> (3,5) ・式渡しが不正の場合、error終了 [(a,b)](1,2)=> -> [MyErr]Invalid no-name equation ・引数の要素数が異なる場合、error終了(関数の引数と異なり、厳格に判別する) [(a,b,c)=<(a,b)](3,=<(i,2i))=> -> [MyErr]Invalid args.length=3(no-name) |
|
目次
末尾return 入力仕様 |
末尾returnの入力仕様と付随する留意事項について記述する
無名callの末尾returnの仕様を列挙する ・式渡し記号=<を複数列挙の場合、末尾returnのみ取り出す(途中return不可) [=<1,=<2,=<3]=> || [=<3]=> -> 3 [(a)=<1,(a)=<2,(a)=<a](3)=> || [(a)=<a](3)=> -> 3 ・式変数名symbolを式読出しの場合、末尾returnの式渡し記号{=<}を省略可 clear; f(x)=<x; [=<{=<f}]=>g || [=<f]=>g; g(3)=> -> 3 厳密表記 ⇔ 省略表記 =<{=<} ⇔ =< ==<{=<} ⇔ ==< =<{==<} ⇔ ==< Ver.2.260.61以降、対応 ・Ver.2.259.61以降、末尾returnのids未継承の実装不具合を修正 clear; f(x)=<x,[=<{=<f}]=>g; g(3)=> -> 3 clear; [f(x)=<x,=<{=<f}]=>g; g(3)=> -> 厳密表記:{}の中身を式読出し clear; f(x)=<x,[=<{=<f}]=>g; g(3)=> -> 3 clear; [f(x)=<x,=<{=<f}]=>g; g(3)=> -> clear; f(x)=<x,[(a)=<{=<f}](2)=>g; g(3)=> -> 3 clear; [f(x)=<x,(a)=<{=<f}](2)=>g; g(3)=> -> clear; f(x)=<x,[(a)=<{f(a)=>}/*resolved*/](2)=> -> 2 clear; [f(x)=<x,(a)=<{f(a)=>}/*resolved*/](2)=> -> 2 clear; f(x)=<x,[(a)=<{f(a)=>}](2)=>g; g=> -> 2 clear; [f(x)=<x,(a)=<{f(a)=>}](2)=>g; g=> -> 2 clear; f(x)=<x,[(a)=<=<{f(a)=>}/*not-resolved*/](2)=> -> [MyErr]Invalid BTe([object Object]) clear; [f(x)=<x,(a)=<=<{f(a)=>}/*not-resolved*/](2)=> -> [MyErr]Invalid BTe([object Object]) clear; f(x)=<x,[(a)=<=<{f(a)=>}](2)=>g; g=> -> 2 clear; [f(x)=<x,(a)=<=<{f(a)=>}](2)=>g; g=> -> 2 clear; [(a)=<{(a)=<a}](2)=>g; g(3)=> -> 3 clear; a=1, f(x)=<a*x,[(a)=<{=<f}](2)=>g; g(3)=> -> 3 clear; a=1, [f(x)=<a*x,(a)=<{=<f}](2)=>g; g(3)=> -> clear; a=1, [f(x)=<a*x,(a)=<{=<f}](2)=>g; g(3)=> -> 6 clear; a=1, f(x)=<a*x,[(a)==<{=<f}](2)=>g; g(3)=> -> 6 clear; a=1, [f(x)=<a*x,(a)==<{=<f}](2)=>g; g(3)=> -> clear; a=1, [f(x)=<a*x,(a)=<{=<f}](2)=>g; g(3)=> -> 6 clear; a=1, [f(x)=<a*x+b,(a,b)=<{=<f}](2,3)=>g; g(3)=> -> 9 省略表記:末尾returnの式渡し記号{=<}を省略 clear; f(x)=<x; [=<f]=>g; g(3)=> -> 3 clear; f(x)=<x; [(a)=<f](2)=>g; g(3)=> -> 3 clear; f(x)=<x; [(a)=<f(a)=>](2)=> -> 2 clear; f(x)=<x; [(a)=<f(a)=>](2)=>g; g=> -> 2 clear; [(a)=<(a)=<a](2)=>g; g(3)=> -> 3 clear; a=1, f(x)=<a*x; [(a)=<f](2)=>g; g(3)=> -> 3 clear; a=1, f(x)=<a*x; [(a)==<f](2)=>g; g(3)=> -> 6 留意事項を列挙する ・末尾returnの参照要素はlast行列関数の参照要素に一致 clear; (({=<(x)=<x,=<(x)=<-x},=<(x)=<x*x))=>f; f(3)=> -> -3 clear; (last({=<(x)=<x,=<(x)=<-x},=<(x)=<x*x))=>f; f(3)=> -> -3 clear; (first({=<(x)=<x,=<(x)=<-x},=<(x)=<x*x))=>f; f(3)=> -> 3 ・Ver.2.255.59以降、行列への参照の場合、遅延評価の式渡し記号=<を明示 clear; (=<(x)=<x:=<(x)=<-x:=<(x)=<x*x)[0]=>f || (=<(x)=<x)=>f; f(3)=> -> 3 clear; (=<(x)=<x:=<(x)=<-x:=<(x)=<x*x)[1]=>f || (=<(x)=<-x)=>f; f(3)=> -> -3 clear; (=<(x)=<x:=<(x)=<-x:=<(x)=<x*x)[2]=>f || (=<(x)=<x*x)=>f; f(3)=> -> 9 ・行列への参照省略の場合、末尾return clear; (=<(x)=<x:=<(x)=<-x:=<(x)=<x*x)=>f || (=<(x)=<x*x)=>f; f(3)=> -> 9 ・遅延評価の式渡し記号=<省略の場合、末尾return clear; (=<x:=<-x:=<x*x)=>f || (=<x*x)=>f; f=> -> [MyErr]Invalid binary operation clear; (x=3,=<x:=<-x:=<x*x)=>f || (x=3,=<x*x)=>f; f=> -> 9 clear; (=<=<x:=<=<-x:=<=<x*x)=>f || (=<=<x*x)=>f; f=> -> [MyErr]Invalid binary operation clear; (=<=<x:=<=<-x:=<=<x*x)=>f || (=<=<x*x)=>f; x=3; f=> -> 9 clear; ((x)=<x:(x)=<-x:(x)=<x*x)=>f || ((x)=<x*x)=>f; f(3)=> -> [MyErr]Invalid args.length=1(null) clear; ((x)=<x:(x)=<-x:(x)=<x*x)(3)=>f || ((x)=<x*x)(3)=>f; f=> -> 9 ・別途、末尾再帰call最適化は未対応(call stackに依存) |
|
目次
引数省略call |
引数省略callの入力仕様と付随する留意事項について記述する
Non-strict-modeの場合、式変数の明示的な引数省略のcallを許容する(error終了に変更の可能性あり) ・Ver.2.253.59以降、本仕様を廃止 clear; a=2; f(x)=<a; f=> -> 2 clear; a=2; [(x)=<a]()=> -> 2 strict-mode clear; a=2; f(x)=<a; f=> -> [MyErr]Invalid args.length=1(f) clear; a=2; [(x)=<a]()=> -> [MyErr]Invalid args.length=1(null) 留意事項を列挙する ・式読出し記号=>省略不可 |
|
目次
高階関数 入力仕様 |
高階関数を列挙する
・switch高階関数 ・総和高階関数 ・総乗・総積高階関数 ・再帰高階関数 ・微分高階関数 ・積分高階関数 |
|
目次
switch 高階関数 入力仕様 |
switch高階関数
・任意個数の条件分岐による処理を実行する ・条件文と成立時に実行する処理を対にしてcolon:区切りで引数を渡す ・引数の左から順に条件文を判定する ・条件文が成立の場合、対の処理を実行して終了する ・条件文が不成立の場合、対の処理は実行されない switch(第1引数,=<第2引数:第3引数,=<第4引数:...) switch((第1引数,=<第2引数):(第3引数,=<第4引数):...) switch({第1引数:=<第2引数}:{第3引数:=<第4引数}:...) ・引数 ・第奇数番引数: 0||not0の実数値を返す条件文を値渡し ・第偶数番引数: 条件文成立時の展開式を式渡し||symbol渡し ・返値 条件文成立時: 対の処理の演算結果を返す 全条件文不成立時: 値を返す場合 switch(第1引数,第2引数:第3引数,第4引数:...) ・引数 ・第奇数番引数: 0||not0の実数値を返す条件文を値渡し ・第偶数番引数: 条件文成立時の返値を値渡し ・返値 条件文成立時: 対の返値を返す 全条件文不成立時: Nativeのif文を一例に示す if(x >= 4) return 4; else if(x > 3) return 3; else if(x > 2) return 2; else return -x; ・対の処理を値渡しで記述する場合 x=2; switch(x>=4,4:x>3,3:x>2,2:1,-x) -> -2 x=2; switch(ge(x,4),4:gt(x,3),3:gt(x,2),2:1,-x) -> -2 ・値渡しの場合、行列要素の演算を実行後、次の実行文を実行する x=2; switch(0,4:0,3:0,2:1,-2) -> -2 ・対の処理を式渡しで記述する場合、条件文が成立のcaseのみ実行する x=2; switch(x>=4,=<4:x>3,=<3:x>2,=<2:1,=<{-x}) -> -2 x=2; switch(ge(x,4),=<4:gt(x,3),=<3:gt(x,2),=<2:1,=<{-x}) -> -2 論理演算子をbit演算子で代替する場合、括弧を明示するか関数を使用する ・if(1==1 || 1==-1) return 1; switch((1==1)|(1==-1),1) || switch(eq(1,1)|eq(1,-1),1) || switch(1|0,1) -> 1 ・if(1==1 && 1==-1) return 1; switch((1==1)&(1==-1),1) || switch(eq(1,1)&eq(1,-1),1) || switch(1&0,1) -> ・Ver.2.59.26以降、論理演算子を追加 switch(1==1||1==-1,1) || switch((1==1)||(1==-1),1) || switch(1||0,1) -> 1 switch(1==1&&1==-1,1) || switch((1==1)&&(1==-1),1) || switch(1&&0,1) -> test caseを列挙する switch(0) -> switch(1) -> switch(i) -> switch(1,0) -> 0 switch(1,1) -> 1 switch(1,i) -> i switch(i,1) -> switch(0,0:1,2:3,4) -> 2 switch(0,0:1i,2:3,4) -> 4 switch(0,0:real(1i),2:3,4) -> 4 switch(0,0:imag(1i),2:3,4) -> 2 switch(0,0:1(1-i),2:3,4) -> 2 switch(0,0:real(1(1-i)),2:3,4) -> 2 switch(0,0:imag(1(1-i)),2:3,4) -> 2 switch(1,=<{1}) -> 1 switch(0:1,=<{1}) -> 1 switch(0,0:1,=<{1}) || switch((0,0):(1,=<{1})) || switch({0:0}:{1:=<{1}}) -> 1 switch(0,0,1,=<{1}) // NG -> switch(0,0:0,0:0,0:1,=<{1}:1,=<{2}) -> 1 clear; b=1; a=<b=2; b=<b; switch(0,a:1,=<b) -> 2 clear; b=1; a=<b=2; b=<b; switch(1,=<b:0,a) -> 2 clear; b=1; a=<b=2; b=<b; switch(1,=<b:0,=<a) -> 1 clear; b=1; a=<b=2; b=<b; switch(0,=<a:1,=<b) -> 1 ・Ver.2.157.38以降、論理演算子(短絡評価)を追加 clear; b=0; a=<b=1; 0|||a,b -> (0,1) clear; b=0; a=<b=1; 1|||a,b -> (1,0) clear; b=0; a=<b=1; c=<b=-1; a|||c,b -> (0,-1) |
|
目次
総和 高階関数 入力仕様 |
総和高階関数
・展開式のdummy変数整数区間[a,b]の総和を演算して返す _s(=<第1引数,第2引数,第3引数[,第4引数]) ・第1引数: dummy変数の展開式を式渡し||symbol渡し ・第2引数: dummy変数の区間下端a(整数)を値渡し ・第3引数: dummy変数の区間上端b(整数)を値渡し option ・第4引数: dummy変数のstep(正の整数)を値渡し[省略時、1] test caseを列挙する ・dummy変数n=1~10のnの総和 _sn(=<{n},1,10) || 1+2+3+4+5+6+7+8+9+10 || (10+1)10/2 -> 55 eqn_n=<n; _sn(=<eqn_n,1,10) || _sn(=<eqn_n=>,1,10) -> 55 ・区間反転を単なる逆順の演算で定義する _Sn(=<{n},10,1) || 10+9+8+7+6+5+4+3+2+1 -> 55 ・dummy変数が負の場合も同様に定義する _sn(=<{n},-10,-1) || -10-9-8-7-6-5-4-3-2-1 -> -55 _Sn(=<{n},-1,-10) || -1-2-3-4-5-6-7-8-9-10 -> -55 _Sn(=<{n},1,-3) || 1+0-1-2-3 -> -5 ・以降、dummy変数に0を含めて記述する ・step=2の場合 _sn(=<{n},0,10,2) || 0+2+4+6+8+10 -> 30 _Sn(=<{n},10,0,2) || 10+8+6+4+2+0 -> 30 _Sn(=<{n},1,-3,2) || 1-1-3 -> -3 ・step<1の場合、暗黙で既定値に変換 _sn(=<{n},0,10,0) || _sn(=<{n},0,10,1) -> 55 ・step<0の場合、暗黙で絶対値に変換 _sn(=<{n},0,10,-2) || _sn(=<{n},0,10,2) -> 30 _Sn(=<{n},10,0,-2) || _Sn(=<{n},10,0,2) -> 30 ・n=0~10の行列の総和 _sn(=<{(n,2n:3n,4n)},N=2,5N) -> (55,110:165,220) _Sn(=<{(n,2n:3n,4n)},10,0) -> (55,110:165,220) ・2変数の多重総和 _sy(=<{_sx(=<{x+y},0,y)},0,2) || 0+1+2+2+3+4 -> 12 _Sy(=<{_Sx(=<{x+y},y,0)},2,0) || 4+3+2+2+1+0 -> 12 _sy(=<{_Sx(=<{x+y},y,0)},0,2) || 0+2+1+4+3+2 -> 12 _Sy(=<{_sx(=<{x+y},0,y)},2,0) || 0+2+3+4+1+2 -> 12 ・総和を取るdummy変数はscope変数から独立 x=-1; y=-2; _sy(=<{_sx(=<{x+y},0,y)},0,2); x+y -> -3 ・高階関数の引数は最終行vectorの左から順に参照 _sn(,is=0,:,ie=10,:=<{n},is,ie) -> 55 ・dummy変数は変数の命名規則に準拠 _smax(=<{0},1,2) -> [MyErr]Invalid max called _spi(=<{0},1,2) -> [MyErr]Invalid pi called _s3(=<{0},1,2) -> [MyErr]Invalid 3 called _s3n(=<{0},1,2) -> [MyErr]Invalid FNh called ・配列を使用 x={0,1,2,3,4,5,6,7,8,9}; _sn(=<x[n],0,9) -> 45 x={0,1,2,3,4,5,6,7,8,9:0,-1,-2}; _sn(=<x[n],0,9) -> (45,39) 応用例を示す ・1回試行で当たりの確率をPb[%]とする ・10回試行中、n回当たりの確率Pn[%]を式変数で定義する clear; Pb=3; Pn=<{100combin(10,n)(Pb/100)^n((100-Pb)/100)^(10-n)}; n=0; Pn -> 73.74241268949281 n=1; Pn -> 22.806931759636946 n=2; Pn -> 3.1741606057226677 n=3; Pn -> 0.2617864417090862 n=4; Pn -> 0.014168853803842281 n=5; Pn -> 0.0005258543679776511 n=6; Pn -> 0.000013552947628290013 n=7; Pn -> 2.3952190212e-7 n=8; Pn -> 2.7779602049999973e-9 n=9; Pn -> 1.909250999999996e-11 n=10; Pn -> 5.904899999999982e-14 ・10回試行中、N回以上当たりの確率[%] N=10; _sn(=<Pn,N,10) || 100(Pb/100)^N -> 5.904899999999982e-14 N=9; _sn(=<Pn,N,10) -> 1.9151558999999963e-11 N=8; _sn(=<Pn,N,10) -> 2.7971117639999973e-9 N=7; _sn(=<Pn,N,10) -> 2.42319013884e-7 N=6; _sn(=<Pn,N,10) -> 0.000013795266642174013 N=5; _sn(=<Pn,N,10) -> 0.0005396496346198251 N=4; _sn(=<Pn,N,10) -> 0.014708503438462106 N=3; _sn(=<Pn,N,10) -> 0.27649494514754835 N=2; _sn(=<Pn,N,10) -> 3.4506555508702164 N=1; _sn(=<Pn,N,10) -> 26.257587310507166 N=0; _sn(=<Pn,N,10) -> 99.99999999999999 |
|
目次
総乗・総積 高階関数 入力仕様 |
総乗・総積高階関数
・展開式のdummy変数整数区間[a,b]の総乗・総積を演算して返す _p(=<第1引数,第2引数,第3引数[,第4引数]) ・第1引数: dummy変数の展開式を式渡し||symbol渡し ・第2引数: dummy変数の区間下端a(整数)を値渡し ・第3引数: dummy変数の区間上端b(整数)を値渡し option ・第4引数: dummy変数のstep(正の整数)を値渡し[省略時、1] test caseを列挙する ・dummy変数n=1~10のnの総乗 _pn(=<{n},1,10) || 1*2*3*4*5*6*7*8*9*10 -> 3628800 eqn_n=<n; _pn(=<eqn_n,1,10) || _pn(=<eqn_n=>,1,10) -> 3628800 ・区間反転を単なる逆順の演算で定義する _Pn(=<{n},10,1) || 10*9*8*7*6*5*4*3*2*1 -> 3628800 ・dummy変数が負の場合も同様に定義する _pn(=<{n},-3,-1) || (-3)(-2)(-1) -> -6 _Pn(=<{n},-1,-3) || (-1)(-2)(-3) -> -6 _Pn(=<{n},1,-3) || (1)(0)(-1)(-2)(-3) -> 0 ・step=2の場合 _pn(=<{n},1,10,2) || 1*3*5*7*9 || 9!! -> 945 _Pn(=<{n},10,1,2) || 10*8*6*4*2 || 10!! -> 3840 _Pn(=<{n},1,-3,2) || (1)(-1)(-3) -> 3 ・step=3の場合 _pn(=<{n},1,2,3) || 1 -> 1 _Pn(=<{n},2,1,3) || 2 || 2!!! -> 2 ・n=1~2の行列の総積 An=<(n,2n:3n,4n); _pn(=<{An},1,2) || (1,2:3,4)(2,4:6,8) -> (14,20:30,44) An=<(n,2n:3n,4n); _Pn(=<{An},2,1) || (2,4:6,8)(1,2:3,4) -> (14,20:30,44) ・2変数の多重総乗 _py(=<{_px(=<{(x*y)},1,y)},1,3) || (1*1)(1*2)(2*2)(1*3)(2*3)(3*3) -> 1296 _Py(=<{_Px(=<{(x*y)},y,1)},3,1) || (3*3)(2*3)(1*3)(2*2)(1*2)(1*1) -> 1296 _py(=<{_Px(=<{(x*y)},y,1)},1,3) || (1*1)(2*2)(1*2)(3*3)(2*3)(1*3) -> 1296 _Py(=<{_px(=<{(x*y)},1,y)},3,1) || (1*3)(2*3)(3*3)(1*2)(2*2)(1*1) -> 1296 ・任意行列Aの累乗 A=(1,2:3,4); N=2; _pn(=<{A},1,N) -> (7,10:15,22) A=(1,2:3,4); N=5; _pn(=<{A},1,N) -> (1069,1558:2337,3406) A=(1,2:3,4); N=5; _pn(=<{trans(A)},1,N) -> (1069,2337:1558,3406) ・複素数の任意行列cAの累乗 cA=(e^{i(pi/4)},:,e^{i(-pi/4)}); N=4; _pn(=<{cA},1,N) -> (-1+2.7755575615628914e-16i,0:0,-1-2.7755575615628914e-16i) ・配列を使用 x={0,1,2,3,4,5,6,7,8,9}; _pn(=<x[n],0,9) -> 0 x={0,1,2,3,4,5,6,7,8,9}; _pn(=<x[n],1,9) -> 362880 |
|
目次
再帰 高階関数 入力仕様 |
再帰高階関数
・展開式の演算結果をdummy変数に代入する操作を再帰回数繰り返す ・最後の演算結果を返す ・Ver.2.242.56以降、再帰高階関数のみ、dummy変数名symbolを省略可(while文の代替) ・Ver.2.381.86以降、繰り返し回数=1~のdummy変数を一時的に保持する予約変数__n__を追加 clear; _r(=<arr.push(__n__),arr=[],10); arr -> (1,2,3,4,5,6,7,8,9,10) _r(=<第1引数,第2引数,第3引数[,=<第4引数]) ・第1引数: dummy変数の展開式を式渡し||symbol渡し ・第2引数: dummy変数の初期値を値渡し||Ver.2.271.62以降、式渡し||symbol渡し clear; A0=(1,2:3,4); _r((A)=<A+A0,=<A0,10) -> ・第3引数: 再帰回数(正の整数)を値渡し option Ver.2.30.15以降、第4引数追加 ・第4引数: 再帰処理の反復後break条件(not0でbreak)を式渡し||symbol渡し[省略時、break判定なし] static scopes2d arrayを共有するため、引数指定のbreak判定は反復後に実施 test caseを列挙する ・再帰回数<=0の場合、初期値を返す _rn(=<{n+1},3,-1) -> 3 ・加算の漸化式 _rn(=<{n+1},,0) -> 0 _rn(=<{n+1},,1) -> 1 _rn(=<{n+1},,2) -> 2 ・同義 eqn_n=<n+1; _rn(=<eqn_n,,2) -> 2 _rn(=<eqn_n=>,eqn_n=<n+1,2) -> 2 Pn=0; _rn(=<{Pn=Pn+1},0,2); Pn -> 2 _rn(=<{Pn=Pn+1},Pn=0,2); Pn -> 2 ・初期値未定義の場合、error終了 clear; _rn(=<{Pn=Pn+1},,2); Pn -> [MyErr]Invalid binary operation ・非同義(変数への代入は0が返る) clear; _rn(=<{n=n+1},,2) // NG -> 0 clear; _rn(=<{n=n+1},,2); n -> [MyErr]Invalid REv(n) clear; _rn(=<{n=n+1},n=0,2); n -> 0 ・乗算の漸化式 _rn(=<{n*2},1,0) -> 1 _rn(=<{n*2},1,1) || 2^1 -> 2 _rn(=<{n*2},1,2) || 2^2 -> 4 _rn(=<{n*2},1,3) || 2^3 -> 8 ・同義 Pn=1; _rn(=<{Pn=Pn*2},0,3); Pn -> 8 _rn(=<{Pn=Pn*2},Pn=1,3); Pn -> 8 ・任意行列Aの累乗 An=(1,:,1); A=(1,2:3,4); N=2; _rn(=<{An=An*A},,N); An -> (7,10:15,22) _rn(=<{An=An*(1,2:3,4)},An=(1,:,1),5); An -> (1069,1558:2337,3406) ・2変数の多重再帰 _ry(=<{_rx(=<{x+y},1,2)},1,2) || (1+(3))+3/*(x)+y*/ -> 7 _Ry(=<{_Rx(=<{x+y+1},1,2)},1,2) -> 13 Ver.2.30.15以降、第4引数追加 ・第4引数で再帰処理の反復後break条件を指定可 単なるfor-loopのため、call stackの制限はない(再帰回数||反復後break条件で終了) ・test caseを列挙する _rn(=<{n+1},,100,=<1) -> 1 _rn(=<{n+1},,100,=<{n>=50}) -> 51 _rn(=<{n+1},,1000000,=<{n>=500000}) -> 500001 _rn(=<{Pn=Pn+1},Pn=0,100,=<{Pn>=50}); Pn -> 50 _rn(=<{Pn=Pn+1},Pn=0,100,=<{n>=50}); Pn -> 100 _rn(=<{last{Pn=Pn+1,Pn}},Pn=0,100,=<{n>=50}); Pn -> 51 _rn(=<{Pn=Pn*2},Pn=1,10,=<{Pn>100}); Pn -> 128 _rn(=<{last{Pn=Pn*2,n+1}},Pn=1,10,=<{Pn>100}) -> 7 _ry(=<{_rx(=<{x+y},1,2,=<{y==1})},1,2) || (1+(2))+2/*(x)+y*/ -> 5 階乗の一例10!=3628800を示す ・n=10を初期値に設定 ・Pn=1を初期値とする漸化式last{Pn=Pn*n,n-1}を設定 ・一般的な再帰回数上限値1e6を設定 ・反復後break条件にn==1を設定 _rn(=<{last{Pn=Pn*n,n-1}},last(Pn=1,10),1e6,=<{n==1}),Pn -> (0,3628800) ・Pn=Pn*1の演算後、n-1して0が返る ・自明の演算Pn=Pn*1を除く場合、反復後break条件にn==2を設定 _rn(=<{last{Pn=Pn*n,n-1}},last(Pn=1,10),1e6,=<{n==2}),Pn -> (1,3628800) ・同様に、Pn=Pn*2の演算後、n-1して1が返る 応用例を示す ・非線形方程式の解法を使用 ・絶対誤差指定で収束判定条件を設定する場合 clear; run=<last{mdx=Newton(=<{x0+2*x1=5,3*x0+4*x1=6},=<{x0,x1})}; _rn(=<run,Nmax=10,Nmax,=<{normc(mdx)<1e-3}); normc(mdx) -> 2.0548659974995737e-10 clear; run=<last{mdx=Newton(=<{x0+2*x1=5,3*x0+4*x1=6},=<{x0,x1})}; _rn(=<run,Nmax=10,Nmax,=<{normc(mdx)<1e-12}); normc(mdx) -> infoLost[ri] 2.2204460494935903e-15 ・相対誤差指定で収束判定条件を設定する場合 clear; run=<last{mdx=Newton(=<{x0+2*x1=5,3*x0+4*x1=6},=<{x0,x1})}; _rn(=<run,Nmax=10,Nmax,=<{normc(mdx)/normc({x0,x1})<1e-3}); normc(mdx) -> 2.0548659974995737e-10 normc(mdx)/normc({x0,x1}) -> 3.4129466559497216e-11 clear; run=<last{mdx=Newton(=<{x0+2*x1=5,3*x0+4*x1=6},=<{x0,x1})}; _rn(=<run,Nmax=10,Nmax,=<{normc(mdx)/normc({x0,x1})<1e-12}); normc(mdx) -> infoLost[ri] 2.2204460494935903e-15 normc(mdx)/normc({x0,x1}) -> infoLost[ri] 3.6879601533907295e-16 |
|
目次
微分 高階関数 入力仕様 |
微分高階関数
・連続関数のdummy変数微分位置における微分係数を有限差分法で数値的に演算して返す ・精度優先で微分位置に応じた情報落ちを対策する ・数値誤差O(dx^4以上)を含み、演算結果に目安の解析誤差を表示する ・1階微分の差分刻み実数値dxD既定値dxD= ・微分位置xでの差分刻みdx既定値 Ver.2.321.78以降、dx=dxD((real(x)||1)+(imag(x)||1)i) _d(=<第1引数,第2引数[,第3引数[,第4引数]]) Ver.2.857.158以降、第2引数の省略不可 ・第1引数: dummy変数の展開式を式渡し||symbol渡し option ・第2引数: 微分位置aを値渡し Ver.2.857.158以降、第2と第3の引数順序の交換 ・第3引数: 微分階数Ndash(正の整数)を値渡し[省略時、1] Ver.2.857.158以降、厳密に判定 ・第4引数: 1階微分の差分刻みdx0を値渡し[0||省略時、dx既定値] 数値誤差に関する精度次数について記述する ・数値誤差は絶対誤差 ・微分階数が1階上がる毎に差分刻み2倍を仮定 stencilに応じたdx=dx0*2^(Ndash-1) ・微分階数が2階までは中心差分法による4次精度以下 ・微分階数が3階以降は中心差分法による2次精度以下 詳細は微分の数値解法参照 test caseを列挙する ・f(x)=(x+i)^5のx=1における微分を示す x=1; dxD=1e-3; dx=max(1,abs(x))dxD(1+i); f=<{(x+i)^5} -> stored_eqn(f) ・0階微分 _dx(=<f,) || _dx(=<f,0) -> -4.000000000000002-4.000000000000001i f -> -4.000000000000002-4.000000000000001i ・1階微分は4次精度 _dx(=<f,1) -> -19.999999999980833-1.6714783492484858e-13i+O(1e-12+1e-12i) _dx(=<f) -> -19.999999999980833-1.6714783492484858e-13i+O(1e-12+1e-12i) ・2階微分は4次精度以下 ・差分刻みが異なる多重化とは完全には一致しない _dx(=<f,2) -> -39.99999999980588+39.99999999944028i+O(3e-10+2e-11i) _dx(=<{_dx(=<f)}) -> -40.00000000012216+40.00000000037086i+O(7e-10+1e-12i) ・2階微分を4次精度1階微分で厳密に多重化する場合、4次精度以下 _dx(=<{_dx(=<f,1,x,1dx)},1,x,2dx) -> -39.99999999980588+39.99999999944028i+O(3e-10+2e-11i) ・3階微分以降は2次精度 ・多重化は1階上がる毎に精度悪化 _dx(=<f,3) -> 2.6203811256259035e-11+120.00084001140233i+O(2e-2+2e-2i) _dx(=<{_dx(=<{_dx(=<f)})}) -> 4.378068605950494e-8+120.00000084539053i+O(2e-7+2e-7i) ・3階微分を4次精度1階微分で厳密に多重化する場合、3次精度以下 _dx(=<{_dx(=<{_dx(=<f,1,x,1dx)},1,x,2dx)},1,x,4dx) -> -3.5859384520417787e-10+120.00000000321582i+O(3e-8+3e-8i) ・4階微分 _dx(=<f,4) -> 120.00000006268098+120.0000001718161i+O(1e+0+2e-2i) _dx(=<{_dx(=<{_dx(=<{_dx(=<f)})})}) -> 120.00001615650766+120.00019838028798i+O(1e-4+7e-7i) ・4階微分を4次精度1階微分で厳密に多重化する場合、2次精度以下 _dx(=<{_dx(=<{_dx(=<{_dx(=<f,1,x,1dx)},1,x,2dx)},1,x,4dx)},1,x,8dx) -> 119.99999887453464+120.00000028081901i+O(2e-6+1e-7i) ・5階微分 _dx(=<f,5) -> 120.00007406068326-0.0000085816675963221i+O(2e+1+2e+1i) _dx(=<{_dx(=<{_dx(=<{_dx(=<{_dx(=<f)})})})}) -> 119.18659727305976+0.3620753183716584i+O(5e-2+5e-2i) ・5階微分を4次精度1階微分で厳密に多重化する場合、2次精度以下 _dx(=<{_dx(=<{_dx(=<{_dx(=<{_dx(=<f,1,x,1dx)} ,1,x,2dx)},1,x,4dx)},1,x,8dx)},1,x,16dx) -> 120.00037113527502-0.000050238369357712915i+O(5e-5+5e-5i) ・6階微分 _dx(=<f,6) -> -0.0004498352662456228+0.0005560189878646384i+O(2e+2+4e+0i) _dx(=<{_dx(=<{_dx(=<{_dx(=<{_dx(=<{_dx(=<f)})})})})}) -> -322.002293591315+54.781879309774695i+O(3e+1+2e-1i) ・6階微分を4次精度1階微分で厳密に多重化する場合、2次精度以下 _dx(=<{_dx(=<{_dx(=<{_dx(=<{_dx(=<{_dx(=<f,1,x,1dx)} ,1,x,2dx)},1,x,4dx)},1,x,8dx)},1,x,16dx)},1,x,32dx) -> -0.004201126114795549+0.005541058257682469i+O(1e-3+5e-5i) ・7階微分 _dx(=<f,7) -> -0.0007280114418273857+0.0030141311391229672i+O(9e+2+9e+2i) _dx(=<{_dx(=<{_dx(=<{_dx(=<{_dx(=<{_dx(=<{_dx(=<f)})})})})})}) -> -177398.93670986558-669172.3211788241i+O(1e+4+1e+4i) ・7階微分を4次精度1階微分で厳密に多重化する場合、2次精度以下 _dx(=<{_dx(=<{_dx(=<{_dx(=<{_dx(=<{_dx(=<{_dx(=<f,1,x,1dx)} ,1,x,2dx)},1,x,4dx)},1,x,8dx)},1,x,16dx)},1,x,32dx)},1,x,64dx) -> -0.009902789205100404+0.05048924924402281i+O(5e-3+5e-3i) ・8階微分 _dx(=<f,8) -> 0.03950452954492218+0.04027593568552271i+O(4e+3+6e+1i) ・9階微分 _dx(=<f,9) -> -0.16566502311270223-0.015219989707358128i+O(4e+3+3e+3i) ・10階微分 _dx(=<f,10) -> 0.044163954487214524-0.06480605313760723i+O(3e+3+6e+1i) ・微分位置を大きくした場合 _dx(=<{x^2},1,1e10) -> 20000000000.027855-2.790277777777778e-12i+O(1e+28+1e-12i) _dx(=<{x^2},2,1e10) -> 1.9999999995176474+9.657789228690995e-20i+O(2e+29+3e+10i) _dx(=<{x^2},3,1e10) -> 1.894235601707095e-17-5.686908543633962e-27i+O(2e+15+5e-4i) ・微分位置を小さくした場合 _dx(=<{x^2},1,1e-10) -> 2.0000000041847774e-10+7.305374602696278e-19i+O(1e-12+1e-12i) _dx(=<{x^2},2,1e-10) -> 2.0000000000000013+9.411477191714447e-16i+O(3e-10+2e-11i) _dx(=<{x^2},3,1e-10) -> 1.5072697186506098e-13-7.131763305997033e-14i+O(2e-2+2e-2i) ・2変数の多重微分 _Dy(=<{_Dx(=<{x*y*y},1,0)},1,1) -> 1.9999999999998288+1.8785308474662037e-13i+O(7e-10+1e-12i) Ver.2.29.15以降、微分の差分刻みdx0=0の場合、省略に同義として扱う _dx(=<{x^2},1,1,0) || _dx(=<{x^2},1,1) -> 1.9999999999998392+1.6112448952215134e-13i+O(1e-12+1e-12i) 応用例を示す ・非線形方程式の解法を使用 ・微分方程式(x^3)"+x-7(1+i)=0の解析解x=1+iの求解 clear; f=<{_dx(=<{x^3},2)+x-7(1+i)=0}; run=<last(mdx=Newton(=<f,=<{x}),max(normc(f),normc(mdx))); _rn(=<run,,6) -> infoLost[ri] 2.3549912261033786e-10+O(8e+0) x -> infoLost[ri] 0.9999999999877383+1.0000000000273828i+O(1e-5+9e-6i) ・normがMachine epsilonまで収束困難のため、一定の反復回数で打切る ・次に数値解の一例を示す clear; f=<{2x*_dx(=<{x*exp(3x)})=i}; run=<last(mdx=Newton(=<f,=<{x}),max(normc(f),normc(mdx))); _rn(=<run,,12) -> 3.844899655887233e-14+O(8e+0) x -> -0.17989326929739397-0.5079280004968542i+O(2e-1+5e-1i) ・続けて厳密解同等の数値解を示す clear; f=<{2x*(1*exp(3x)+x*exp(3x)3)=i}; run=<last(mdx=Newton(=<f,=<{x}),max(normc(f),normc(mdx))); _rn(=<run,,12) -> infoLost[r ] 3.3306690738754696e-16 x -> infoLost[r ] -0.17989326929046887-0.5079280004963925i ・連立方程式の解析解{x0,x1}={1,1}の求解 clear; f0=<{1*x0^2+x1}; f1=<{i*x1^3+x0}; x=<{x0,x1}; f=<{x0+x1=2,_dx0(=<{f0})+_dx1(=<{f1},2)=2+6i}; run=<last(mdx=Newton(=<f,=<x),max(normc(f),normc(mdx))); _rn(=<run,,12) -> infoLost[ri] 3.236567392072123e-11+O(7e+0) x -> ( infoLost[ri] 1.000000000003112+3.106688703682062e-12i+O(6e-5+5e-5i): infoLost[ri] 0.9999999999968879-3.106688703682063e-12i+O(1e-5+2e-5i) ) ・同じく実数演算の場合 clear; f0=<{1*x0^2+x1}; f1=<{i*x1^3+x0}; x=<{x0,x1}; f=<{x0+x1=2,_dx0(=<{f0})+_dx1(=<{f1},2)=2+6i}; run=<last(mdx=Newton(=<f,=<x),max(normc(f),normc(mdx))); _rn(=<run,,12) -> 7.724854831493598e-14+O(7e+0) x -> (1.000000000000009+O(3e-5):0.9999999999999909+O(3e-5)) |
|
目次
積分 高階関数 入力仕様 |
積分高階関数
・連続関数のdummy変数積分区間[a,b]における定積分を有限差分法で数値的に演算して返す ・数値誤差O(dxI^4以上)を含み、演算結果に目安の解析誤差を表示する ・積分区間の分割数の既定値NI= ・積分の差分刻みdxI=(b-a)/NI ・Ver.2.858.159以降、NI=0の場合、初期値0を返す _i(=<第1引数,第2引数,第3引数[,第4引数]) ・第1引数: dummy変数の展開式を式渡し||symbol渡し ・第2引数: dummy変数の積分下端aを値渡し ・第3引数: dummy変数の積分上端bを値渡し option ・第4引数: 積分区間の分割数NI(正の偶数)を値渡し[省略時、NI既定値] 数値誤差に関する精度次数について記述する ・数値誤差は絶対誤差 ・既定で合成Simpson公式による4次精度 ・台形公式による2次精度を内部optionで選択可 詳細は積分の数値解法参照 test caseを列挙する ・f(x)=x^4の積分区間[0,1+i]における定積分を示す a=0; b=1+i; ab=[a,b]; f=<{x^4} -> stored_eqn(f) ・分割数100 _ix(=<f,ab) || _ix(=<f,a,b) -> -0.8000000053333336-0.8000000053333334i+O(1e-8+1e-8i) ・分割数10 _ix(=<f,ab,10) -> -0.8000533333333335-0.8000533333333333i+O(1e-4+1e-4i) ・分割数1000 _ix(=<f,ab,1000) -> -0.8000000000005332-0.800000000000533i+O(1e-12+1e-12i) ・積分区間を反転 _ix(=<f,[b,a]) || _ix(=<f,b,a) -> 0.8000000053333336+0.8000000053333334i+O(1e-8+1e-8i) ・分割数が奇数の場合、暗黙で+1して偶数に変換される _ix(=<f,ab,99) || _ix(=<f,ab,99+1) -> -0.8000000053333336-0.8000000053333334i+O(1e-8+1e-8i) ・分割数が負の場合、暗黙で絶対値に変換される _ix(=<f,ab,-100) -> -0.8000000053333336-0.8000000053333334i+O(1e-8+1e-8i) ・2次精度選択の場合(参考) _ix(=<f,ab) -> -0.8001333320000001-0.8001333319999999i+O(1e-4+1e-4i) ・2変数の多重積分 _iy(=<{_ix(=<{x^2*y},0,y)},0,2) -> 2.1333333475555563+O(2e-7) _iy(=<{y^4/3},0,2) -> 2.1333333475555563+O(2e-7) ・微分・積分 _ix(=<{_dx(=<{x^3})},1,2) -> 7.000000000000061-3.369899113923336e-14i+O(1e-8+1e-14i) _Ix(=<{_Dx(=<{sin(x)},1,0)},-pi,pi) -> 6.283185307180439+2.010557877134426e-14i+O(2e-5+8e-14i) ・積分・微分 _dx(=<{_ix(=<{x^3},0,x)},1,2) -> 7.999999999998895+5.517384388870678e-13i+O(4e-5+2e-5i) ・目安の解析誤差が当てにならないcase _it(=<sqrt(tan(t)),0,pi/4,1) -> 0.4678848567030397+O(2e-2) _it(=<sqrt(tan(t)),0,pi/4,10) -> 0.48570913091719253+O(4e-5) _it(=<sqrt(tan(t)),0,pi/4,100) -> 0.487438986531867+O(4e-9) _it(=<sqrt(tan(t)),0,pi/4,1000) -> 0.4874937074650109+O(4e-13) _it(=<sqrt(tan(t)),0,pi/4,10000) -> 0.48749543789153654+O(4e-17) _it(=<sqrt(tan(t)),0,pi/4,100000) -> 0.4874954926124276+O(4e-21) ・Ver.2.806.130以降、DE求積法 _i0((t)=<sqrt(tan(t)),0,pi/4) -> infoLost[r ] 0.48749549439936113+O(1e-100) 1/sqrt(2)*(log(sqrt(2)-1)+pi/2) -> 0.48749549439936113 ・広義積分 _i0((t)=<1/sqrt(t),0,1) -> infoLost[r ] 1.9999999768287098+O(1e-100) _i0((t)=<1/sqrt(-t),-1,0) -> 1.9999999768287098+O(1e-100) 応用例を示す ・非線形方程式の解法を使用 ・f(x)=x^2のx=[0,b]の定積分=3^3/3となる積分方程式の解析解b=3の求解 clear; f=<{_ix(=<{x^2},0,b)=3^3/3}; run=<last(mdx=Newton(=<f,=<{b},=<{1}),max(normc(f),normc(mdx))); _rn(=<run,,12) -> infoLost[ i] 1.3839478914652153e-28+O(8e-7) b -> infoLost[ri] 2.9999999999999996+4.613167602434132e-34i+O(1e-1+2e-1i) ・2次関数の積分の場合、補間多項式に一致するため、数値誤差が出ない _ix(=<{x^2},0,3,2) -> 9+O(5e+0) _ix(=<{x^2},0,3,10) -> 8.999999999999998+O(8e-3) _ix(=<{x^2},0,3,100) -> 8.999999999999998+O(8e-7) _ix(=<{x^2},0,3,1000) -> 8.999999999999998+O(8e-11) ・f(x)=x^4のx=[0,b]の定積分=3^5/5となる積分方程式の解析解b=3の求解 clear; f=<{_ix(=<{x^4},0,b)=3^5/5}; run=<last(mdx=Newton(=<f,=<{b},=<{1}),max(normc(f),normc(mdx))); _rn(=<run,,20) -> 1.4210854715508634e-14+O(8e-7) b -> infoLost[r ] 2.9999999959999992-1.15251646351758e-21i+O(2e-2+2e-2i) ・高次関数の積分の場合、収束までの反復回数が増える ・得られる近似解の精度は分割数に依存する _ix(=<{x^4},0,3,2) -> 50.62499999999998+O(5e+0) _ix(=<{x^4},0,3,10) -> 48.60323999999998+O(8e-3) _ix(=<{x^4},0,3,100) -> 48.60000032400001+O(8e-7) _ix(=<{x^4},0,3,1000) -> 48.60000000003241+O(8e-11) |
|
目次
高階行列関数 入力仕様 |
高階行列関数を列挙する
・Jacobi高階行列関数 ・Newton高階行列関数 ・ODE高階行列関数 ・Ver.2.238.56以降、ODEt高階行列関数 |
|
目次
Jacobi 高階行列関数 入力仕様 |
Jacobi高階行列関数
・Jacobi行列を有限差分法で数値的に演算して返す(Newton法参照) ・1次精度の数値誤差O(dx)を含む Ver.2.323.78以降、演算結果に目安の解析誤差を表示する ・1階偏微分の差分刻み実数値dxJ既定値dxJ= ・微分位置xでの差分刻みdx既定値 Ver.2.321.78以降、微分位置に応じて差分刻みを可変(情報落ちの対策とNewton高階行列関数の反復過程の改善) Ver.2.321.78以降、dx=dxJ((real(x)||1)+(imag(x)||1)i) Ver.2.840.146以降、訂正 Ver.2.404.86以降、false指定の場合、実数の相対値dx=dxJ(real(x)||1) Ver.2.840.146以降、訂正 Jacobi(=<第1引数,=<第2引数[,=<第3引数[,第4引数]]) ・第1引数: 方程式||関数式の列vectorを式渡し||symbol渡し option ・第3引数: 未知変数初期値の列vectorを式渡し||symbol渡し[0||省略時、zeros-vector] ・第4引数: 偏微分の差分刻みdxを値渡し[0||省略時、dx既定値] xの1次方程式の偏微分係数を求める場合 clear; Jacobi(=<{3x-3=0},=<{x},=<{0}) -> -3.0000000000098264+9.826647183188544e-12i clear; Jacobi(=<{3x-3=0},=<{x}) -> -3.0000000000098264+9.826647183188544e-12i ・右辺に移項した関数=-3x+3のx=0周辺の傾き-3を返す xの2次関数の偏微分係数を求める場合 clear; Jacobi(=<{2x^2},=<{x},=<{1}) -> 4.0000200000131025+0.000019999986898147652i ・1階偏微分の解析解=4xからx=1周辺の傾き4を返す 微分位置を大きくした場合 clear; Jacobi(=<{2x^2},=<{x},=<{1e10}) // NG -> 19999999999.999996+19999999999.999996i clear; a=1e10; h=max(1,abs(a))1e-5(1+i); Jacobi(=<{2x^2},=<{x},=<{a},h) // OK -> 40000200000.65538+199999.3446694911i ・情報落ちの対策が必要 ・1階偏微分の解析解=4xからx=1e10周辺の傾き4e10を返す test caseを列挙する clear; Jacobi(=<{y},=<{x},=<{1}) -> [MyErr]Invalid BRsa operation clear; Jacobi(=<{x},=<{x},=<{1}) -> 1.0000000000032756-3.2755706022246335e-12i clear; Jacobi(=<{x},=<{x*x},=<{1}) -> [MyErr]Invalid binary operation clear; Jacobi(=<{x},=<x,=<{1}) -> [MyErr]Invalid =<eqn clear; Jacobi(=<x,=<{x},=<{1}) -> [MyErr]Invalid =<eqn clear; Jacobi(=<{x},=<{x},=<{1,2}) -> [MyErr]Invalid J arguments clear; Jacobi(=<{x**2},=<{x},=<(1,2)) -> 4.000010000057512+0.000009999942489061227i clear; Jacobi(=<{x**2:x},=<{x},=<{1}) -> 1.0000000000032756-3.2755706022246335e-12i clear; Jacobi(=<{x},=<{(0,x)},=<{1}) -> 1.0000000000032756-3.2755706022246335e-12i clear; Jacobi(=<{x},=<{(x,0)},=<{1}) -> [MyErr]Invalid J arguments clear; Jacobi(=<{(x+i)**2},=<{x},=<{0}) -> 0.000009999976914767357+2.000009999990017i clear; Jacobi(=<{(x+i)**2},=<{x},1000) -> 0.000009999976914767357+2.000009999990017i clear; Jacobi(=<{(x+i)**2},1000,1000) -> [MyErr]Invalid jacobian arguments clear; x=<x; y=<x*x; Jacobi(=<{y},=<x,=<{1}) -> 2.0000100000065513+0.000009999993448815332i clear; x=<x*x; y=<x*x; Jacobi(=<{y},=<x,=<{1}) -> [MyErr]Invalid binary operation clear; x=<x*x; y=<x*x; Jacobi(=<{y},=<{x},=<{1}) -> 2.0000100000065513+0.000009999993448815332i clear; Jacobi(=<{x0**2+x1,x0+x1**2},=<{x0,x1},=<{1,2}) -> ( 2.0000100000065513+0.000009999993449073826i,1.0000000000032756-3.2755706022246335e-12i: 0.999999999981071+1.8928929719024988e-11i,4.000010000057512+0.000009999942489061227i ) ・実数演算の場合 clear; Jacobi(=<{x0**2+x1,x0+x1**2},=<{x0,x1},=<{1,2}) -> ( 2.00001000001393,1.0000000000065512: 0.9999999999621422,4.000010000027032 ) |
|
目次
Newton 高階行列関数 入力仕様 |
Newton高階行列関数
・Newton法による反復1回の演算結果を返す ・引数は第4引数までJacobi高階行列関数に同じ ・返値は符号付の解の修正vector(以降、残差と呼ぶ) ・絶対誤差の残差norm収束判定実数値epsN既定値epsN= Ver.2.309.77以降、判定対象の残差normがNaNの場合、無条件にbreak Newton(=<第1引数,=<第2引数[,=<第3引数[,第4引数[,第5引数[,第6引数[,第7引数[,第8引数]]]]]]) ・第1引数: 方程式||関数式の列vectorを式渡し||symbol渡し option ・第3引数: 未知変数初期値の列vectorを式渡し||symbol渡し[0||省略時、zeros-vector] ・第4引数: 偏微分の差分刻みdxを値渡し[0||省略時、dx既定値] Ver.2.29.15以降、第5~7引数追加 ・第5引数: 反復回数(正の整数)を値渡し[省略時、1] ・第6引数: 反復後判定の絶対誤差の残差norm収束判定実数値epsNを値渡し[省略時、epsN既定値] static scopes2d arrayを共有するため、引数指定のbreak判定は反復後に実施 ・第7引数: 第6引数epsNを相対誤差に変換する0||not0のflag[省略時、0] Ver.2.408.86以降、第8引数追加 ・第8引数: 収束計算のretry機能を使用する0||not0のflag[省略時、0] 最大retry回数<反復回数-1 retry時、初期値を乱数でresetして反復継続 Ver.2.410.86以降、最終反復回数の場合、retry無効で反復終了(NaN確定) Ver.2.834.140~2.836.141以降、連立方程式の列挙順序:昇順 ⇒ Fisher-Yates shuffle Ver.2.871.164以降、pivot選択の処理順を修正(retry機能の問題を解消) 応用例は連立方程式の解法参照 test caseを列挙する ・symbol渡し clear; x=<{x0,x1}; x_initial=<{0,0}; f=<{x0+2*x1=5,3*x0+4*x1=6}; run=<last(mdx=Newton(=<f,=<x,=<x_initial),max(normc(f=>),normc(mdx))); _rn(=<run,,3) -> infoLost[ri] 2.2204460494935903e-15 ・strict-modeで直接式渡しする場合 clear; run=<last(mdx=Newton(=<{x0+2*x1=5,3*x0+4*x1=6},=<{x0,x1},=<{0,0}),normc(mdx)); _rn(=<run,,3) -> infoLost[ri] 2.2204460494935903e-15 ・strict-modeの最短表記 clear; _rn(=<{ last(mdx=Newton(=<{x0+2*x1=5,3*x0+4*x1=6},=<{x0,x1},=<{0,0}),normc(mdx)) },,3) -> infoLost[ri] 2.2204460494935903e-15 Ver.2.29.15以降 ・第3引数0の場合、zeros-vector ・第4引数0の場合、偏微分の差分刻みdx=dx既定値 ・第5引数で反復回数を指定可 ・第6引数で絶対誤差の収束判定値を指定可 ・第7引数で第6引数を相対誤差に変換するflagを指定可 ・反復回数<=0の場合、初期値を返す clear; mdx=Newton(=<{x0+2*x1=5,3*x0+4*x1=6},=<{x0,x1},,,0); normc(mdx) -> 0 {x0,x1} -> (0:0) ・残差の最大値を演算する場合、転置行列関数を使用 ・残差を結合した列vectorを転置して行vectorに変換後、maxを取る max(trans({mdx,-mdx})) // real-part -> 0 max(i*trans({mdx,-mdx})) // imag-part -> 0 camax(trans(mdx)) // |both-part| -> 0 ・反復3回の場合 ・反復最後の残差を目安の解析誤差として表示する clear; mdx=Newton(=<{x0+2*x1=5,3*x0+4*x1=6},=<{x0,x1},,,3); normc(mdx) -> infoLost[ri] 2.2204460494935903e-15 max(trans({mdx,-mdx})) // real-part -> infoLost[ri] 1.7763568394338757e-15 max(i*trans({mdx,-mdx})) // imag-part -> infoLost[ri] 2.1963410797410362e-20 camax(trans(mdx)) // |both-part| -> infoLost[ri] 1.7763568395696568e-15 {x0,x1} -> ( infoLost[ri] -3.999999999999999-3.362471994400586e-26i+O(2e-15+2e-20i): infoLost[ri] 4.499999999999999+6.466216308756395e-26i+O(1e-15+2e-20i) ) ・反復10回以内に絶対誤差のnorm収束判定値1e-8を指定する場合 ・収束判定成立時の残差を目安の解析誤差として表示する clear; mdx=Newton(=<{x0+2*x1=5,3*x0+4*x1=6},=<{x0,x1},,,10,1e-8); normc(mdx) -> 2.0548659974995737e-10 max(trans({mdx,-mdx})) // real-part -> 1.0355938329098548e-10 max(i*trans({mdx,-mdx})) // imag-part -> 1.0355819825427455e-10 camax(trans(mdx)) // |both-part| -> 1.464542464160083e-10 {x0,x1} -> ( -4.000000000000001+2.1963377172690418e-20i+O(1e-10+1e-10i): 4.500000000000001-1.7499160954924154e-20i+O(1e-10+1e-10i) ) ・反復10回以内に相対誤差のnorm収束判定値1e-8を指定する場合 ・未知変数の初期化が必要 ・zeros-vectorで初期化の場合、反復2回以上が確定する clear; {$x0,$x1}={,}; mdx=Newton(=<{x0+2*x1=5,3*x0+4*x1=6},=<{x0,x1},,,10,1e-8*normc({x0,x1})); normc(mdx) -> infoLost[ri] 2.2204460494895584e-15 1e-8*normc({x0,x1}) -> infoLost[ri] 6.02079728939615e-8+O(2e-33i) normc(mdx)/normc({x0,x1}) -> infoLost[ri] 3.6879601533840316e-16+O(1e-41i) max(trans({mdx,-mdx})) // real-part -> infoLost[ri] 1.7763568395916467e-15 max(i*trans({mdx,-mdx})) // imag-part -> infoLost[ri] 2.250213020433239e-25 camax(trans(mdx)) // |both-part| -> infoLost[ri] 1.7763568395916467e-15 {x0,x1} -> ( infoLost[ri] -4.000000000000001+1.9139665347514104e-25i+O(2e-15+2e-25i): infoLost[ri] 4.500000000000001-1.4354751880569493e-25i+O(1e-15+2e-25i) ) ・反復10回以内に相対誤差のnorm収束判定値1e-8を指定する場合 ・第7引数で相対誤差のflag-ONを指定する場合、未知変数の初期化不要 clear; mdx=Newton(=<{x0+2*x1=5,3*x0+4*x1=6},=<{x0,x1},,,10,1e-8,1); normc(mdx) -> 2.0548659974995737e-10 normc(mdx)/normc({x0,x1}) -> 3.4129466559497216e-11+O(4e-22+4e-22i) max(trans({mdx,-mdx})) // real-part -> 1.0355938329098548e-10 max(i*trans({mdx,-mdx})) // imag-part -> 1.0355819825427455e-10 camax(trans(mdx)) // |both-part| -> 1.464542464160083e-10 {x0,x1} -> ( -4.000000000000001+2.1963377172690418e-20i+O(1e-10+1e-10i): 4.500000000000001-1.7499160954924154e-20i+O(1e-10+1e-10i) ) ・反復1回指定で3回繰り返した場合 ・反復1回目の最大残差が目安の解析誤差として残る clear; _rn(=<{ mdx=Newton(=<{x0+2*x1=5,3*x0+4*x1=6},=<{x0,x1},,,1) },,3); normc(mdx) -> infoLost[ri] 2.2204460494935903e-15+O(2e-5+5e-6i) max(trans({mdx,-mdx})) // real-part -> infoLost[ri] 1.7763568394338757e-15+O(2e-5) max(i*trans({mdx,-mdx})) // imag-part -> infoLost[ri] 2.1963410797410362e-20+O(1e-5) camax(trans(mdx)) // |both-part| -> infoLost[ri] 1.7763568395696568e-15+O(2e-5) {x0,x1} -> ( infoLost[ri] -3.999999999999999-3.362471994400586e-26i+O(4e+0+2e-10i): infoLost[ri] 4.499999999999999+6.466216308756395e-26i+O(4e+0+1e-5i) ) |
|
目次
ODE 高階行列関数 入力仕様 |
ODE高階行列関数
・dummy変数を媒介する常微分方程式の1step定積分を有限差分法で数値的に演算して返す ・数値誤差O(dt^4以上)を含み、演算結果に目安の解析誤差を表示する _o(=<第1引数,=<第2引数,=<第3引数,第4引数,第5引数[,第6引数[,第7引数[,第8引数]]]) Ver.2.858.159以降、更新 ・第1引数: 1階常微分方程式右辺の関数式を式渡し||symbol渡し option ・第3引数: 未知変数初期値の列vectorを式渡し||symbol渡し[0||省略時、zeros-vector] ・第4引数: dummy変数初期値t0を値渡し Ver.2.858.159以降、省略不可 ・第5引数: Ver.2.858.159以降、dummy変数終了値t1を値渡し Ver.2.858.159以降、dt=(t1-t0)/反復回数 Ver.2.821.134以降、dt=0の場合、初期値を返す(adaptive-stepの場合、無限loopの可能性を排除) Ver.2.29.15以降、第6引数追加 ・第6引数: 反復回数(正の整数)を値渡し[省略時、NI既定値] Ver.2.858.159以降、演算仕様変更 Ver.2.774.119以降、第7引数追加(adaptive-step solver用) ・第7引数: norm比較判定対象|dt|δのδを値渡し[0||省略時、1e-3] Ver.2.777.123以降、第8引数追加(_o0()指定で任意のButcher-tableを使用) ・第8引数: Butcher-tableの行列を式渡し 数値誤差に関する精度次数について記述する ・数値誤差は絶対誤差 ・既定で陽的Runge-Kutta法による4次精度 ・陽的improved Euler法による2次精度を内部optionで選択可 応用例は斜方投射参照 |
|
目次
ODEt 高階行列関数 入力仕様 |
ODEt高階行列関数
・Ver.2.238.56以降、追加 ・ODE高階行列関数と異なり、dummy変数を未知変数vectorに含めて返す _t変数名symbol(=<第1引数,=<第2引数[,=<第3引数[,第4引数[,第5引数[,第6引数[,第7引数]]]]]) ・ODE高階行列関数の第4引数を削除 |
|
目次
symbolic 高階行列関数 入力仕様 |
symbolic高階行列関数
・未知変数名symbol連番0~のij参照の行列を式変数に式代入して0を返す _e(=<第1引数,第2引数,第3引数) ・Ver.2.736.107~2.739.107以降、廃止予定 ・Ver.2.813.131以降、本仕様を廃止 ・f=<(x0,x1:x2,x3) clear; _ef(=<x,2,2) -> 0 ・Ver.2.231.56以降、第1引数のarguments優先 clear; _e((f)=<x,2,2) -> 0 ・Ver.2.268.62以降、同義 clear; _e((=<f)=<x,2,2) -> 0 ・x=<(x0,x1,x2,x3) clear; _ex(=<{x},1,4) -> 0 clear; _ex(=<{x},1,4); x -> [MyErr]Invalid REv(x0) clear; _ex(=<{x},1,4); ($x0,$x1:$x2,$x3)=identity2; x -> (1,0,0,1) clear; x=<(x0,x1,x2,x3); ($x0,$x1:$x2,$x3)=identity2; x -> (1,0,0,1) ・x=<(x0:x1:x2:x3) clear; _ex(=<{x},4,1); ($x0,$x1:$x2,$x3)=identity2; x -> (1:0:0:1) clear; x=<(x0:x1:x2:x3); ($x0,$x1:$x2,$x3)=identity2; x -> (1:0:0:1) ・x=<(x0,x1:x2,x3) clear; _ex(=<{x},2,2); ($x0,$x1,$x2,$x3)=(1,2,3,4); x -> (1,2:3,4) clear; x=<(x0,x1:x2,x3); ($x0,$x1,$x2,$x3)=(1,2,3,4); x -> (1,2:3,4) ・symbol名は最終要素を参照 clear; _ex(=<{test,test:x},2,2); x -> [MyErr]Invalid REv(test0) clear; _ex(=<{test,test:test,x},2,2); x -> [MyErr]Invalid REv(x0) clear; _ex(=<{test,test:test,x},2,2); ($x0,$x1,$x2,$x3)=(1,2,3,4); x -> (1,2:3,4) ・引数不正の場合、error終了 clear; _ex(=<{x},2,0) -> [MyErr]Invalid matrix size clear; _ex(=<{x},2) -> [MyErr]Invalid EX arguments Ver.2.29.15以降、変数の命名規則に準拠 ・Ver.2.232.56以降、symbol表記に統一 ・Ver.2.248.57以降、dummy ⇒ symbol _ex(=<{$x},2,2) -> [MyErr]Invalid Ver.2.32.17以降、第1引数の括弧省略可 clear; _ex(=<x,1,4); ($x0,$x1:$x2,$x3)=identity2; x -> (1,0,0,1) 応用例は逆行列の解法参照 |
|
目次
Euclid実空間 |
3次元Euclid実空間について記述する
前提を列挙する ・右手系をRHS(Right Handed System)と省略する ・左手系をLHS(Left Handed System)と省略する 代数学に準ずる右手系 ・紙面x-y平面に対して鉛直上向きをz軸の正とする(左手系はその逆) ・x軸を親指、y軸を人差し指、z軸を中指とする ・回転方向は、x⇒y⇒z⇒x軸の正循環で各軸に向ける方向を正とする computer graphicsで主流の左手系 ・HTML5描画canvasではbrowser左上originのclient座標系に対して手前方向をCSS/z-indexの正とする 右手系の座標系を列挙する ・複素数平面 ・直交座標 ・平面極座標 ・球面座標 |
|
目次
複素数平面 |
2次元の複素平面(複素数平面||Gauss平面)について記述する
直交座標表示 ・vectorの成分(x,y)を複素数の成分z=x+y*iで表示 ($x,$y)=(1,-1); vec=(x,y); vec -> (1,-1) z=complex(vec); z -> 1-i x=real(z); x -> 1 y=imag(z); y -> -1 ・vector空間の標準内積 vec0=(1,1); vec1=(1,-1); dot_(vec0,vec1)=<vec0*trans(vec1); dot_(=<vec0,=<vec1) || (1,1){1,-1} -> 0 z0=complex(vec0); z0 -> 1+i z1=complex(vec1); z1 -> 1-i cdot_(z0,z1)=<(real(z0),imag(z0))*{real(z1),imag(z1)}; cdot_(z0,z1) || cdot(z0,z1) -> 0 極座標表示 ・vectorの長さrと偏角tの成分(r,t)を複素数の極形式r*e^(i(t))で表示 ($x,$y)=(1,-1); vec=(x,y); vec -> (1,-1) r=normc(trans(vec)); r -> 1.4142135623730951 t=atan2(y,x); t -> -0.7853981633974483 z=pcomplex(r,t); z -> 1.0000000000000002-i r=abs(z); r -> 1.4142135623730951 t=arg(z); t -> -0.7853981633974482 |
|
目次
直交座標 |
右手系の直交座標について記述する
直交座標(x,y,z)の関係式を示す ・定義 e_0:={0,0,0} e_x:={1,0,0} e_y:={0,1,0} e_z:={0,0,1} I:=(e_x,e_y,e_z) ・基底vector(不変) e_x={1,0,0} e_y={0,1,0} e_z={0,0,1} ・標準内積 e_x・e_x=1 e_x・e_y=0 e_x・e_z=0 e_y・e_x=0 e_y・e_y=1 e_y・e_z=0 e_z・e_x=0 e_z・e_y=0 e_z・e_z=1 ・右手系のvector積(外積) e_x×e_x=e_0 e_x×e_y=e_z e_x×e_z=-e_y e_y×e_x=-e_z e_y×e_y=e_0 e_y×e_z=e_x e_z×e_x=e_y e_z×e_y=-e_x e_z×e_z=e_0 ・運動 位置 (vec_x):={x,y,z} 速度 (vec_x)'={x',y',z'} 加速度 (vec_x)"={x",y",z"} 面積速度vec_vA*2=(vec_x)×(vec_x)'={y*z'-z*y',z*x'-x*z',x*y'-y*x'} |
|
目次
平面極座標 |
右手系の平面極座標について記述する
平面極座標(r,p)の関係式を示す ・平面に直交するz軸周りの回転行列 rotz=(cos(p),-sin(p),0:sin(p),cos(p),0:0,0,1) ・定義 e_0:={0,0,0} e_x:={1,0,0} e_y:={0,1,0} e_z:={0,0,1} I:=(e_x,e_y,e_z) rotz:=(e_r,e_p,e_z)=I*rotz ・基底vector(2軸可変) e_r={cos(p),sin(p),0} e_p={-sin(p),cos(p),0} e_z={0,0,1} ・基底vectorの時間微分 (e_r)'=p'*e_p (e_p)'=-p'*e_r (e_z)'=e_0 (e_r)"=p"*e_p-(p')^2*e_r (e_p)"=-p"*e_r-(p')^2*e_p (e_z)"=e_0 ・回転行列の時間微分 (rotz)':=((e_r)',(e_p)',(e_z)')=p'*(e_p,-e_r,e_0) (rotz)":=((e_r)",(e_p)",(e_z)")=p"*(e_p,-e_r,e_0)+p'*(-p'*e_r,-p'*e_p,e_0) ・標準内積 e_r・e_r=1 e_r・e_p=0 e_r・e_z=0 e_p・e_r=0 e_p・e_p=1 e_p・e_z=0 e_z・e_r=0 e_z・e_p=0 e_z・e_z=1 ・右手系のvector積(外積) e_r×e_r=e_0 e_r×e_p=e_z e_r×e_z=-e_p e_p×e_r=-e_z e_p×e_p=e_0 e_p×e_z=e_r e_z×e_r=e_p e_z×e_p=-e_r e_z×e_z=e_0 ・運動 位置 (vec_r):=rotz*{r,0,0} 速度 (vec_r)'=(rotz)'*{r,0,0}+rotz*{r',0,0}=rotz*{r',r*p',0} 加速度 (vec_r)"=(rotz)'*{r',r*p',0}+rotz*{r",r'*p'+r*p",0}=rotz*{r"-r*(p')^2,2*r'*p'+r*p",0} 面積速度vec_vA*2=(vec_r)×(vec_r)'=(e_r*r)×(e_r*r'+e_p*r*p')=rotz*{0,0,r^2*p'} ・速度成分 v_r=r' v_p=r*p' v_z=0 ・加速度成分 a_r=r"-r*(p')^2 a_p=r*p"+2*r'*p' a_z=0 |
|
目次
球面座標 |
右手系の球面座標について記述する
球面座標(r,t,p)の関係式を示す ・一般化した回転行列 rot_=(sin(t)*cos(p),cos(t)*cos(p),-sin(p):sin(t)*sin(p),cos(t)*sin(p),cos(p):cos(t),-sin(t),0) ・定義 e_0:={0,0,0} e_x:={1,0,0} e_y:={0,1,0} e_z:={0,0,1} I:=(e_x,e_y,e_z) rot_:=(e_r,e_t,e_p)=I*rot_ ・基底vector(3軸可変) e_r={sin(t)*cos(p),sin(t)*sin(p),cos(t)} e_t={cos(t)*cos(p),cos(t)*sin(p),-sin(t)} e_p={-sin(p),cos(p),0} ・標準内積 e_r・e_r=1 e_r・e_t=0 e_r・e_p=0 e_t・e_r=0 e_t・e_t=1 e_t・e_p=0 e_p・e_r=0 e_p・e_t=0 e_p・e_p=1 |
|
目次
行列積 の解法 |
通常の行列積LR=L*Rのalgorithmについて記述する
通常の行列積LR=L*Rの定義を次に示す ・Lの列sizeとRの行sizeが一致するcaseのみ、積を定義する ・内積 (1,2){3,4} -> 11 ・直積 {1,2}(3,4) -> (3,4:6,8) ・正方行列の累乗 (1,2:0,0)(1,2:0,0) -> (1,2:0,0) (3,4:0,0)(3,4:0,0) -> (9,12:0,0) 行列sizeの異なる次のLとRを一例に示す L=(1,2:3:4,5:6); R=(1,2:3,4,5); ・演算子による行列積L*R L*R -> (7,10,10:3,6,0:19,28,25:6,12,0) ・行列size sizer(L) -> 4 sizec(L) -> 2 sizer(R) -> 2 sizec(R) -> 3 sizer(L*R) -> 4 sizec(L*R) -> 3 ・行列sizeについて次の関係が成立する sizer(L*R)=sizer(L) -> 0 sizec(L*R)=sizec(R) -> 0 以上より、行列積のalgorithmを以下に示す ・L指定行とR指定列の内積を取る式変数productを定義する ・さらに、行列積LRを返す式変数LpRを定義する LpR=<{product=<last{LR[ir][ic]=ttL[ir]trans((trans(ttR))[ic])}, ttL=trans(trans(L)), ttR=trans(trans(R)), LR=zeros(sizer(ttL),sizec(ttR)), _sir(=<{_sic(=<product,0,sizec(ttR)-1)},0,sizer(ttL)-1), =<LR}=>; ・Ver.2.192.44以降、dot演算子を追加 LpR=<{product=<LR[ir][ic]=ttL[ir](ttR.)[ic]., ttL=L.., ttR=R.., LR=zeros(sizer(ttL),sizec(ttR)), _sir(=<{_sic(=<product,0,sizec(ttR)-1)},0,sizer(ttL)-1), =<LR}=>; ・演算子による行列積L*Rでは1回の転置trans(R)に最適化される ・また、この転置時にRの欠損要素を埋める trans(R) -> (1,3:2,4:0,5) ・さらに、Lの欠損要素の部分はRと内積を取らない(自明の演算は行わない) 行列積L*Rの演算量を多少減らすため、欠損要素を許容する ・N次下三角行列Lの場合、最高効率で演算量が半減する ・行列積の乗算回数を以下に比較して示す ・欠損要素を許容しない場合 N=4; N*N*N -> 64 N=10; N*N*N -> 1000 ・欠損要素を許容する場合 N=4; _sn(=<{n*n},1,N) -> 30 N=10; _sn(=<{n*n},1,N) -> 385 ・4次下三角行列Lの行列積 L=(1:2,3:4,5,6:7,8,9,10); R=identity4; LpR -> (1,0,0,0:2,3,0,0:4,5,6,0:7,8,9,10) L*R -> (1,0,0,0:2,3,0,0:4,5,6,0:7,8,9,10) test caseを列挙する ・上記例 L=(1,2:3:4,5:6); R=(1,2:3,4,5); LpR -> (7,10,10:3,6,0:19,28,25:6,12,0) L*R -> (7,10,10:3,6,0:19,28,25:6,12,0) ・定義できない行列積 ・Ver.2.88.32以降、定義できない乗算||減算||加算を拡張行列演算に追加 L=(1,2); R=(1,2); L*R -> [MyErr]Invalid matrix operation LpR -> (2,4) L*R -> (1,4) ・内積 L=(1+i,1); R={1-i,1}; LpR -> 3 L*R -> 3 ・直積 L={1-i,1}; R=(1+i,1); LpR -> (2,1-i:1+i,1) L*R -> (2,1-i:1+i,1) ・積の演算順序の交換関係 rand_M(m,n)=<zeros(m,n).map((x)=<complex(rand(),rand())*10); L=rand_M(3,2),R=rand_M(2,2); L*R=(R.*L.). -> (0,0:0,0:0,0) L*R=(R'*L')' -> (0,0:0,0:0,0) |
|
目次
補間法 |
補間法を列挙する
・線形近似 ・線形補間 ・Lagrange補間 ・spline補間 |
|
目次
線形近似 |
線形近似について記述する
1次関数 y=f(x)=a*x+b ・傾き:a ・切片:b ・独立変数:x ・従属変数:y 回帰直線 ・通常回帰:y方向の残差の二乗和を最小化する直線 ・主成分回帰:垂線の残差の二乗和を最小化する直線 相関 ・相関係数の区間:[-1,1] ・強い:|相関係数|>0.7 ・弱い:|相関係数|<0.4 ・正:相関係数>0(x増でy増) ・負:相関係数<0(x増でy減) 非線形な系で線形近似の条件(|相関係数|≒1の許容誤差範囲内) ・線形応答(xとyの関係が線形領域):平衡状態に対する変動量が相対的に小さい(変動の振幅が微小) |
|
目次
線形補間 |
線形補間について記述する
1次のLagrange補間 ・1次の補間多項式P1(x)を定義する P1(x)=(1,x)(l:m) ・独立する2点の制御点(xi,f[i])から P1(x0)=(1,x0)(l:m)=f[0] P1(x1)=(1,x1)(l:m)=f[1] ・次の連立線形方程式V1*y1=r1を解くことで V1=(1,x0:1,x1) y1=(l:m) r1=(f[0]:f[1]) ・P1(x)の係数vector y1が求まる ・VはVandermonde行列 ・制御点がすべて独立であればVの逆行列が一意に存在する ・予め逆行列を解いた方が丸め誤差の影響を受けにくい ・その形式に変形したLagrange基底の補間多項式を導出する m=(f[0]-f[1])/(x0-x1) l=f[0]-(f[0]-f[1])/(x0-x1)*x0 (l:m)=(-x1/(x0-x1),x0/(x0-x1):1/(x0-x1),-1/(x0-x1))(f[0]:f[1]) ・y1=inverse(V1)*r1から ・V1の逆行列inverse(V1) inverse(V1)=(-x1/(x0-x1),x0/(x0-x1):1/(x0-x1),-1/(x0-x1)) ・P1(x)=(1,x)(l:m)=(1,x)*inverse(V1)*(f[0]:f[1])から ・1次のLagrange基底多項式のvector L1=(1,x)*inverse(V1) L1=(1,x)(-x1/(x0-x1),x0/(x0-x1):1/(x0-x1),-1/(x0-x1)) =((x-x1)/(x0-x1),(x-x0)/(x1-x0)) ・1次のLagrange型の補間多項式 P1(x)=L1*(f[0]:f[1]) L1=((x-x1)/(x0-x1),(x-x0)/(x1-x0)) ・以上より、制御点の基底vectorが得られる Lj(xi)=(Kdelta(i,0),Kdelta(i,1),...,Kdelta(i,j)) |
|
目次
Lagrange 補間 |
Lagrange補間について記述する
主な用途 ・計算||実験で得られる標本点の補間(制御点の取り方でRunge現象の数値誤差が発生しやすい) 2次のLagrange補間 ・2次の補間多項式P2(x)を定義する P2(x)=(1,x,x^2)(l:m:n) ・独立する3点の制御点(xi,f[i])から P2(x0)=(1,x0,x0^2)(l:m:n)=f[0] P2(x1)=(1,x1,x1^2)(l:m:n)=f[1] P2(x2)=(1,x2,x2^2)(l:m:n)=f[2] ・次の連立線形方程式V2*y2=r2を解くことで V2=(1,x0,x0^2:1,x1,x1^2:1,x2,x2^2) y2=(l:m:n) r2=(f[0]:f[1]:f[2]) ・P2(x)の係数vector y2が求まる ・以下、1次のcaseを拡張して ・2次のLagrange型の補間多項式 P2(x)=L2*(f[0]:f[1]:f[2]) L2=( (x-x1)(x-x2)/(x0-x1)(x0-x2), (x-x0)(x-x2)/(x1-x0)(x1-x2), (x-x0)(x-x1)/(x2-x0)(x2-x1)) test caseを示す xi={0,1,2}; fi={3,5,2}; k=min(sizer(xi),sizer(fi))-1; ・Ver.2.157.38以降、switch高階関数代替の論理演算子(短絡評価)を追加 ljx(j,x)=<_pm(=<{switch(m==j,1:1,=<(x-xi[m])/(xi[j]-xi[m]))},0,k); lji(j,i_)=<_pm(=<m==j&&&1|||(xi[i_]-xi[m])/(xi[j]-xi[m]),0,k); ljx(j,x)=<_pm(=<m==j&&&1|||(x-xi[m])/(xi[j]-xi[m]),0,k); Lkx(x)=<_sj(=<fi[j]*ljx(j,x),0,k); ・Lagrange基底の単位行列 (lji(0,0),lji(0,1),lji(0,2):lji(1,0),lji(1,1),lji(1,2):lji(2,0),lji(2,1),lji(2,2)) -> ( 1,0,0: 0,1,0: 0,0,1 ) ・Lagrange基底多項式 ljx(0,0) -> 1 ljx(0,0.5) -> 0.375 ljx(0,1) -> 0 ljx(0,1.5) -> -0.125 ljx(0,2) -> 0 ljx(0,10) -> 36 ・Lagrange型の補間多項式(fiと基底多項式ljxの線形結合) Lkx(0) -> 3 Lkx(0.5) -> 4.625 Lkx(1) -> 5 Lkx(1.5) -> 4.125 Lkx(2) -> 2 Lkx(10) -> -202 |
|
目次
spline 補間 |
spline補間について記述する
主な用途 ・roboticsの場合、3次の自然spline補間(加速度の連続性を重視) ・数値計算の場合、3次の自然spline補間(演算量=Order(N)で低cost) ・computer graphicsの場合、B-spline補間(必ずしも制御点を通らない) 3次の自然spline補間 ・N+1個の制御点(xi,yi) (xi,yi):=(x[i],y[i]), i=0~N dxi:=dx[i]=(x[i+1]-x[i]), i=0~N-1 dyi:=dy[i]=(y[i+1]-y[i]), i=0~N-1 ・区間iの3次多項式と導関数(次数の昇順に列挙) f(x)=y[i]+b[i](x-x[i])+c[i](x-x[i])^2+d[i](x-x[i])^3, f'(x)=b[i]+2c[i](x-x[i])+3d[i](x-x[i])^2, f"(x)=2c[i]+6d[i](x-x[i]), i=0~N-1 3N個の未知変数に対する連立方程式(full-rank) ・3次多項式(N個) b[i]dx[i]+c[i](dx[i])^2+d[i](dx[i])^3=dy[i], i=0~N-1 ・第1次導関数の連続条件(N-1個) b[i]-b[i+1]+2c[i]dx[i]+3d[i](dx[i])^2=0, i=0~N-2 ・第2次導関数の連続条件(N-1個) c[i]-c[i+1]+3d[i]dx[i]=0, i=0~N-2 ・全区間の境界条件(2個) f"(x[0])=0 -> c0=0 f"(x[N])=0 -> c[N-1]+3d[N-1]dx[N-1]=0 ・以上の解析より、b[i]を未知変数とするN元1次の連立方程式Au=rに帰結する 3重帯行列:=A 未知変数vector:=u={b0,b1,... ,b[N-1]} 右辺vector:=r 解析前の連立方程式を座標形式で示す(test case用) ・3N個の未知変数 u={b0,...,b[N-1],c0,...,c[N-1],d0,...,d[N-1]} ・3次多項式(N個) mA0=(1,1,1,...,N,N,N) nA0=(1,N+1,2N+1,...,N,2N,3N) aA0=(dx0,dx0^2,dx0^3,...,dx[N-1],(dx[N-1])^2,(dx[N-1])^3) r0={dy0,...,dy[N-1]} ・第1次導関数の連続条件(N-1個) mA1=(N+1,N+1,N+1,N+1,...,2N-1,2N-1,2N-1,2N-1) nA1=(1,2,N+1,2N+1,...,N-1,N,2N-1,3N-1) aA1=(1,-1,2dx0,3dx0^2,...,1,-1,2dx[N-2],3(dx[N-2])^2) r1={0,...,0} ・第2次導関数の連続条件(N-1個) mA2=(2N,2N,2N,...,3N-2,3N-2,3N-2) nA2=(N+1,N+2,2N+1,...,2N-1,2N,3N-1) aA2=(1,-1,3dx0,...,1,-1,3dx[N-2]) r2={0,...,0} ・全区間の境界条件(2個) mA3=(3N-1,3N,3N) nA3=(N+1,2N,3N) aA3=(1,1,3dx[N-1]) r3={0,0} ・以上をまとめる mA=(mA0,mA1,mA2,mA3) nA=(nA0,nA1,nA2,nA3) aA=(aA0,aA1,aA2,aA3) r={r0,r1,r2,r3} ・test caseを示す x={0,1,2}; y={1,3,2}; aA=(1,1,1,1,1,1,1,-1,2,3,1,-1,3,1,1,3); mA=(1,1,1,2,2,2,3,3,3,3,4,4,4,5,6,6); nA=(1,3,5,2,4,6,1,2,3,5,3,4,5,3,4,6); r={2,-1,0,0,0,0}; coo=(aA:mA:nA); A=coo2mat(coo); A -> ( 1,0,1,0,1,0: 0,1,0,1,0,1: 1,-1,2,0,3,0: 0,0,1,-1,3,0: 0,0,1,0,0,0:/* Ver.2.128.35以降、pivot=0 allowed in pivotting */ 0,0,0,1,0,3 ) u=Gauss_coo(coo:trans(r)); u -> ( infoLost[r ] 2.75: 0.4999999999999999: -1.1102230246251565e-16: -2.25: -0.75: 0.7500000000000001 ) ・COO行列と右辺vectorの一般化 x={0,1,2}; y={1,3,2}; N=min(sizer(x),sizer(y))-1; dx=x[1][0][N][1]-x; dy=y[1][0][N][1]-y; r=vectorc(3*N); coo=zeros(3,10*N-4); _sj(=<last{ n=j+1,j0=3*j,dxi=dx[j],dyi=dy[j], coo[0][j0][1][3]=(dxi,dxi**2,dxi**3), coo[1][j0][1][3]=(n,n,n), coo[2][j0][1][3]=(n,N+n,2*N+n), r[j]=dyi },0,N-1); _sj(=<last{ n=j+1,j0=3*N+4*j,dxi=dx[j], coo[0][j0][1][4]=(1,-1,2*dxi,3*dxi**2), coo[1][j0][1][4]=(N+n,N+n,N+n,N+n), coo[2][j0][1][4]=(n,n+1,N+n,2*N+n) },0,N-2); _sj(=<last{ n=j+1,j0=7*N+3*j-4,dxi=dx[j], coo[0][j0][1][3]=(1,-1,3*dxi), coo[1][j0][1][3]=(2*N+n-1,2*N+n-1,2*N+n-1), coo[2][j0][1][3]=(N+n,N+n+1,2*N+n) },0,N-2); j0=10*N-4-3; coo[0][j0][1][3]=(1,1,3*dx[N-1]); coo[1][j0][1][3]=(3*N-1,3*N,3*N); coo[2][j0][1][3]=(N+1,2*N,3*N); coo -> ( 1,1,1,1,1,1,1,-1,2,3,1,-1,3,1,1,3: 1,1,1,2,2,2,3,3,3,3,4,4,4,5,6,6: 1,3,5,2,4,6,1,2,3,5,3,4,5,3,4,6 ) r -> (2:-1:0:0:0:0) B-spline曲線 ・i=[1,N-1]の区間で一様knotの2次曲線 Si(i_,t)=<0.5*(t^2,t,1)*(1,-2,1:-2,2,0:1,1,0)*{(x[i_-1],y[i_-1]),(x[i_],y[i_]),(x[i_+1],y[i_+1])}; ・N+1個の制御点 x={0,0,1,2,2}; y={1,1,3,2,2}; N=min(sizer(x),sizer(y))-1; N -> 4 ・各区間の媒介変数t=[0,1] Si(1,0) -> (0,1) Si(1,0.5) -> (0.125,1.25) Si(1,1) -> (0.5,2) Si(2,0) -> (0.5,2) Si(2,0.5) -> (1,2.625) Si(2,1) -> (1.5,2.5) Si(3,0) -> (1.5,2.5) Si(3,0.5) -> (1.875,2.125) Si(3,1) -> (2,2) ・重複する制御点のi=1||N-1の区間は線形 |
|
目次
有限差分法 |
有限差分法Finite Difference Methodの解法を列挙する
・微分の数値解法 ・積分の数値解法 |
|
目次
微分 の数値解法 |
有限差分による微分の数値解法について記述する
差分刻みをhとして連続関数f(x)のx周辺の2次打切りTaylor級数から f(x-h)=f(x)+f'(x)(-h)+f"(x)(-h)^2/2!+O(h^3) f(x+h)=f(x)+f'(x)(h)+f"(x)(h)^2/2!+O(h^3) ・1階微分の2次精度中心差分 f'(x)=(f(x+h)-f(x-h))/(2h)+O(h^2) ・2階微分の2次精度中心差分 f"(x)=(f(x+h)-2f(x)+f(x-h))/(h^2)+O(h^2) 2次精度の1階微分を多重化して2階微分を導出 f"(x)=(f'(x+h)-f'(x-h))/(2h)=(f(x+2h)-f(x)-f(x)+f(x-2h))/(2h)^2+O(h) ・本来、2階微分の精度次数が落ちるが、H=2hとすれば精度次数が落ちない f"(x)=(f(x+H)-2f(x)+f(x-H))/(H^2)+O(H^2) ・よって微分階数が1階上がる毎に差分刻み2倍の関係が成立すると仮定して ・3階微分以降も同様に、再帰的に多重化する f'(x)=(f(x+h)-f(x-h))/(2h)+O((h)^2) f"(x)=(f'(x+2h)-f'(x-2h))/(4h)+O((2h)^2) f"'(x)=(f"(x+4h)-f"(x-4h))/(8h)+O((4h)^2) f""(x)=(f"'(x+8h)-f"'(x-8h))/(16h)+O((8h)^2) ... 続いて4次打切りTaylor級数から f(x-2h)=f(x)+f'(x)(-2h)+f"(x)(-2h)^2/2!+f"'(x)(-2h)^3/3!+f""(x)(-2h)^4/4!+O(h^5) f(x-h)=f(x)+f'(x)(-h)+f"(x)(-h)^2/2!+f"'(x)(-h)^3/3!+f""(x)(-h)^4/4!+O(h^5) f(x+h)=f(x)+f'(x)(h)+f"(x)(h)^2/2!+f"'(x)(h)^3/3!+f""(x)(h)^4/4!+O(h^5) f(x+2h)=f(x)+f'(x)(2h)+f"(x)(2h)^2/2!+f"'(x)(2h)^3/3!+f""(x)(2h)^4/4!+O(h^5) ・次の3階微分を消去して f(x+2h)-f(x-2h)=f'(x)(4h)-f"'(x)(2h)^3/3+O(h^5) f(x+h)-f(x-h)=f'(x)(2h)-f"'(x)(h)^3/3+O(h^5) ・1階微分の4次精度中心差分 f'(x)=(8(f(x+h)-f(x-h))-(f(x+2h)-f(x-2h)))/(12h)+O(h^4) さらに、5次打切りTaylor級数から ・次の4階微分を消去して f(x+2h)+f(x-2h)=2f(x)+f"(x)(2h)^2+f""(x)(2h)^4/12+O(h^6) f(x+h)+f(x-h)=2f(x)+f"(x)(h)^2+f""(x)(h)^4/12+O(h^6) ・2階微分の4次精度中心差分 f"(x)=(16(f(x+h)+f(x-h))-(f(x+2h)+f(x-2h))-30f(x))/(12h^2)+O(h^4) 4次精度の1階微分を多重化して2階微分を導出 f"(x)=(8(f'(x+h)-f'(x-h))-(f'(x+2h)-f'(x-2h)))/(12h)+O(h^3) ・2次精度の場合と異なり、必要な離散点数が増えるが、 f'(x+h)=(8(f(x+2h)-f(x))-(f(x+3h)-f(x-h)))/(12h) f'(x-h)=(8(f(x)-f(x-2h))-(f(x+h)-f(x-3h)))/(12h) f'(x+2h)=(8(f(x+3h)-f(x+h))-(f(x+4h)-f(x)))/(12h) f'(x-2h)=(8(f(x-h)-f(x-3h))-(f(x)-f(x-4h)))/(12h) ・stencilが2倍に広がる点は変わらない f'(x+h)-f'(x-h)=(8(f(x+2h)-2f(x)+f(x-2h))-(f(x+3h)-f(x-h)+f(x+h)-f(x-3h)))/(12h) f'(x+2h)-f'(x-2h)=(8(f(x+3h)-f(x+h)-f(x-h)+f(x-3h))-(f(x+4h)-2f(x)+f(x-4h)))/(12h) ・よって再帰的に多重化した場合、微分階数が上がる毎に精度が悪化する f'(x)=(8(f(x+h)-f(x-h))-(f(x+2h)-f(x-2h)))/(12h)+O(h^4) f"(x)=(8(f'(x+h)-f'(x-h))-(f'(x+2h)-f'(x-2h)))/(12h)+O(h^3) f"'(x)=(8(f"(x+h)-f"(x-h))-(f"(x+2h)-f"(x-2h)))/(12h)+O(h^2) f""(x)=(8(f"'(x+h)-f"'(x-h))-(f"'(x+2h)-f"'(x-2h)))/(12h)+O(h) ... 1階微分を多重化の拡張 ・拡張なし:差分刻み一定 ・拡張あり:1階上がる毎に差分刻み2倍の関係を仮定 2階微分の演算結果 _dx(=<{(x+i)^5},2,1) ・上から順に、2次精度、2次精度拡張、4次精度、4次精度拡張 -> -40.000079995027676+40.000100045239535i+O(5e-4+1e-6i) -> -40.000199999917704+40.00019999969536i+O(2e-4+4e-6i) -> -40.00000000012216+40.00000000037086i+O(7e-10+1e-12i) -> -39.99999999980588+39.99999999944028i+O(3e-10+2e-11i) ・2階微分までは拡張の有無で大差なし 5階微分の演算結果 _dx(=<{(x+i)^5},5,1) ・上から順に、2次精度、2次精度拡張、4次精度、4次精度拡張 -> -2376.9807493302333+2495.6629047556085i+O(2e+4+2e+4i) -> 120.00007406068326-0.0000085816675963221i+O(2e+1+2e+1i) -> 119.18659727305976+0.3620753183716584i+O(5e-2+5e-2i) -> 120.00037113527502-0.000050238369357712915i+O(5e-5+5e-5i) ・3階微分以降は拡張必須 以上より、微分階数の場合分け ・微分階数≤2:4次精度拡張 ・微分階数≥3:2次精度拡張(精度より演算速度を優先) 留意事項を列挙する ・Ver.2.369.86以降、微分高階関数の精度次数を指定可 ・非線形性が強い関数・級数・極限の演算結果は当てにならない f'(x)=(8(f(x+h)-f(x-h))-(f(x+2h)-f(x-2h)))/(12h)+O(h^4) f"(x)=(8(f'(x+2h)-f'(x-2h))-(f'(x+4h)-f'(x-4h)))/(24h)+O(h^3) f"'(x)=(f"(x+4h)-f"(x-4h))/(8h)+O((4h)^2) f""(x)=(f"'(x+4h)-f"'(x-8h))/(16h)+O((8h)^2) ... |
|
目次
積分 の数値解法 |
有限差分による積分の数値解法について記述する
前提を列挙する ・総和をΣ<変数=開始値,終了値>で記述する ・線形結合をvectorの内積で記述する 公式を導出する ・連続関数f(x)の積分区間[a,b]をN等分割して差分刻みをhとする h=(b-a)/N ・分割した離散点xiに対する関数の離散点f[i]を定義する xi:=x[i]=a+i*h, i=0~N f[i]=f(xi) ・分割した微小区間の面積dS[i]と全区間の面積Sを定義する dS[i], i=0~N-1 S=Σ<i=0,N-1>dS[i] ・各変数は列vectorとして添字iで各要素の離散点を参照する 微小区間の関数fを線形補間する場合、2次精度の台形公式 ・微小区間の台形の面積の総和を取ることで dS[0]=(f[0]+f[1])h/2+O(h^3) dS[i]=(f[i]+f[i+1])h/2+O(h^3) S=Σ<i=0,N-1>dS[i]=Σ<i=0,N-1>(f[i]+f[i+1])h/2+O(h^2) ・次の台形公式が導出される S=(f[0]+2Σ<i=1,N-1>f[i]+f[N])h/2+O(h^2) ・両端を除く離散点f[i]は2回足されて2倍 ・全区間の離散化誤差のOrderは微小区間の正方形面積h*h ・総和によって微小区間の離散化誤差が積算されて精度次数が1次落ちる 微小区間の関数fを1次多項式で補間する場合も同様 ・1次のLagrange型の補間多項式 P1(x)=L1*(f[0]:f[1]) L1=((x-x1)/(x0-x1),(x-x0)/(x1-x0)) ・P1(x)の不定積分integral(P1(x)) h=x1-x0 L1=(1/h)(-(x-x1),(x-x0)) integral(P1(x))=(1/2h)(-(x-x1)^2+C[0],(x-x0)^2+C[1])(f[0]:f[1]) ・C[i]は積分定数 ・P1(x)の微小区間[x0,x1]における定積分 dS[0]=(1/2h)(h^2,h^2)(f[0]:f[1])=(h/2)(1,1)(f[0]:f[1])=(f[0]+f[1])h/2 ・以上より、次の台形公式が導出される S=(f[0]+2Σ<i=1,N-1>f[i]+f[N])h/2+O(h^2) 微小区間の関数fを2次多項式で補間する場合、4次精度の合成Simpson公式 ・2次のLagrange型の補間多項式 P2(x)=L2*(f[0]:f[1]:f[2]) L2=( (x-x1)(x-x2)/(x0-x1)(x0-x2), (x-x0)(x-x2)/(x1-x0)(x1-x2), (x-x0)(x-x1)/(x2-x0)(x2-x1)) ・P2(x)の不定積分integral(P2(x)) h=x1-x0=x2-x1 L2=(1/(2h^2))((x-x1)(x-x2),-2(x-x0)(x-x2),(x-x0)(x-x1)) integral(P2(x))=(1/(2h^2))( x^3/3-(x1+x2)x^2/2+x1*x2*x+C[0], -2(x^3/3-(x0+x2)x^2/2+x0*x2*x+C[1]), x^3/3-(x0+x1)x^2/2+x0*x1*x+C[2])(f[0]:f[1]:f[2]) ・C[i]は積分定数 ・P2(x)の微小2区間[x0,x2]における定積分 ・1列目のみ示す x0=x1-h x2=x1+h (x2^3-x0^3)/3-(x1+x2)(x2+x0)(x2-x0)/2+x1*x2(x2-x0) =((x1+h)^3-(x1-h)^3)/3-(2x1+h)(2x1)h+x1(x1+h)2h =(3x1^2+h^2)2h/3-(2x1+h)(x1)2h+x1(x1+h)2h =(3x1^2+h^2-(2x1+h)(x1)3+x1(x1+h)3)2h/3 =(h^2)2h/3 ・2列目以降も同様 ・以上より、次のSimpson公式が導出される dS[0]+dS[1]=(h/3)(1,4,1)(f[0]:f[1]:f[2])+O(h^5) ・さらに、分割数Nは正の偶数を前提として総和を取ることで S=Σ<k=0,N/2-1>(dS[2k]+dS[2k+1])+O(h^4) =(h/3)(Σ<k=0,N/2-1>((1,4,1)(f[2k]:f[2k+1]:f[2k+2])))+O(h^4) ・次の合成Simpson公式が導出される S=(f[0]+4Σ<k=0,N/2-1>f[2k+1]+2Σ<k=1,N/2-1>f[2k]+f[N])h/3+O(h^4) ・両端を除く偶数の離散点f[2k]は2回足されて2倍 ・全区間の離散化誤差のOrderは微小区間の正方形面積h*hの2乗 留意事項を列挙する ・Ver.2.369.86以降、積分高階関数の精度次数を指定可 |
|
目次
有限体積法 |
有限体積法Finite Volume Methodの解法を列挙する
・有限体積法の概要 |
|
目次
有限体積法 の概要 |
有限体積法の概要について記述する
有限体積法は状態量(物理量)のfluxを基準にcontrol volume内の保存則を離散化する ・fluxは離散化した基準面を通過する単位面積当たりの状態量(Fick's first law) ・1次元の場合、x方向の左右の面を通過するfluxを考慮する ・2次元の場合、左右に加えてy方向の上下の面を通過するfluxを考慮する ・3次元の場合、上下左右に加えてz方向の前後の面を通過するfluxを考慮する ・よって単位体積当たりの状態量の時間微分は fluxのdivergence項とsource||sink項の和で表される(Fick's second law) |
|
目次
modelling |
modellingの実施例を列挙する
・0D-RC並列回路simplified modelling ・0D-diffusion simplified modelling ・0D-sea-level simplified modelling ・0D-cell simplified modelling ・0D-heat simplified modelling |
|
目次
0D-RC 並列回路 simplified modelling |
RC並列回路を漸化式で記述する0D-RC並列回路のsimplified modellingについて記述する
1次遅れ系のRC並列回路要素(以降、RC-1次遅れ要素と省略する)のmodellingを一例に示す ・保存則はKirchhoff's laws ・時間を有限差分法で離散化 前提を列挙する ・電流Iと電圧Vは正の相関を前提とする ・Laplace領域における合成impedanceの伝達関数Z(s)は電流I(s)に対する電圧V(s)の比で表す Z(s)=V(s)/I(s) ・RLC直列回路要素のZ(s)を一例に示す Z(s)=R+L*s+1/(C*s) ・各回路要素の電流の変数名をI_要素とする ・各回路要素の電圧の変数名をV_要素とする RC-1次遅れ要素のZ(s)を導出する ・Kirchhoff's Current Law(KCL) I=I_R+I_C ・Kirchhoff's Voltage Law(KVL) V_R-V_C=0 V=V_R=R*I_R V=V_C=I_C/(C*s) ・KVLからI_RとI_Cの関係を得る R*I_R-I_C/(C*s)=0 I_R=I_C/(R*C*s) ・得られたI_RとKCLからI_CとIの関係を得る I=I_C*(1+R*C*s)/(R*C*s) I_C=I*(R*C*s)/(1+R*C*s) ・得られたI_CとKVLからVとIの関係を得る V=I*R/(1+R*C*s) ・以上より、RC-1次遅れ要素のZ(s)が得られる V=I*R/(1+R*C*s) -> Z(s)=R/(1+R*C*s) RC-1次遅れ要素の時間発展方程式を導出する ・得られたVとIの関係から V+V*R*C*s=I*R V*s=-V/(R*C)+I/C ・次の定数を定義する a=1/(R*C) b=1/C ・定数aの物理的な定義を示す 時定数1/a=R*C -> 周期=2pi*R*C cut-off角周波数a=1/(R*C) -> cut-off周波数=1/周期=1/(2pi*R*C) ・以上より、RC-1次遅れ要素の時間発展方程式が得られる V*s=-V/(R*C)+I/C -> V*s=-a*V+b*I 時間微分V*sを離散化して以下の漸化式を得る ・陽解法 newV=(1-a*dt)*oldV+b*dt*I ・陰解法 newV=(oldV+b*dt*I)/(1+a*dt) 各parameterのOrder推定方法を示す ・交流impedance実測結果のs→+∞に漸近する高周波数のZ(s)=R+1/(C*s)からRを推定 ・推定Rとcut-off周波数=1/(2pi*R*C)からCを推定 実施例は0D-cell EIS simulation参照 |
|
目次
0D-diffusion simplified modelling |
1次元拡散方程式を漸化式で記述する0D-diffusionのsimplified modellingについて記述する
porous電極活物質内ionの拡散方程式のmodellingを一例に示す ・物質量||濃度の保存則はFick's laws ・反応物質量の保存則はFaraday's laws ・反応ionの価数を追加考慮 ・活物質の体積分率を追加考慮 ・Ver.2.51.25以降、活物質の形状因子を追加考慮(参考論文[1]) ・時間を有限差分法で離散化 ・空間を有限体積法で離散化 前提を列挙する ・電流Iと電圧Vは正の相関を前提とする ・Faraday定数をF[C/mol]とする ・拡散の代表長さをdxとする ・拡散係数をDsとする ・活物質の体積分率をesとする ・有効拡散係数をDs_effとする(tortuosityによって例えば、Ds_eff=Ds*es^1.5) ・反応ionの価数をnとする ・反応面積(反応界面の総表面積)をSとする ・活物質の形状因子をasとする ・有効反応面積をS*asとする ・ion濃度変化量Δc=代表濃度-平均濃度を定義する ・限界ion濃度をcmaxとする ・比例係数をkとするion濃度変化量Δcと電圧Vの関係式V=Δc/(cmax*k)を仮定する ⇒ θ=c/cmaxにおける微分係数V/Δθの逆数をkとする 1次元拡散方程式の右辺を示す ・活物質内を想定して左右の面のfluxをaboutに仮定する 電解質側の右面flux=I/(n*F*S*as) 活物質側の左面flux=Ds_eff*Δc/dx ・fluxのdivergence項=(右面flux-左面flux)/dx 右辺=-Ds_eff*Δc/dx^2+I/(n*F*S*as*dx) 拡散方程式の時間発展方程式を示す ・Fick's second law es*Δc'=-Ds_eff*Δc/dx^2+I/(n*F*S*as*dx) ・ion濃度変化に伴う電圧に変換する es*cmax*k*V'=-Ds_eff*cmax*k*V/dx^2+I/(n*F*S*as*dx) V'=-Ds_eff*V/(dx^2*es)+I/(n*F*S*as*dx*es*cmax*k) ・次の定数を定義する a=Ds_eff/(dx^2*es) b=1/(n*F*S*as*dx*es*cmax*k) ・RC並列回路のanalogyから定数aの物理的な定義を示す 有効拡散の時定数1/a=(dx^2*es)/Ds_eff 有効拡散のcut-off角周波数a=Ds_eff/(dx^2*es) ・以上より、電圧に変換した拡散方程式の時間発展方程式が得られる V'=-Ds_eff*V/(dx^2*es)+I/(n*F*S*as*dx*es*cmax*k) -> V'=-a*V+b*I 時間微分V'を離散化して以下の漸化式を得る ・陽解法 newV=(1-a*dt)*oldV+b*dt*I ・陰解法 newV=(oldV+b*dt*I)/(1+a*dt) 各parameterのOrder推定方法を示す ・低周波数側の交流impedance実測結果からRC並列回路同様に推定 ・または、充放電後の緩和過程の電圧変化からaを推定 ・推定aと充放電中の電圧変化からbを推定 実施例は0D-cell EIS simulation参照 |
|
目次
0D-sea-level simplified modelling |
海面上昇を漸化式で記述する0D-sea-levelのsimplified modellingについて記述する
・Ver.2.614.96以降、基準年の線膨張量係数k1に対する無次元の重み係数bを適合 simplifiedの仮定 ・時間刻み:1年 ・代表温度:地表の平均気温(海水温を反映可) ・年平均の代表温度上昇量:dT(基準温度に対する相対量) ・dTの積算温度:sum_dT ・海面上昇量:level=level0+level1 海水の熱膨張量:level0 雪氷の融解量:level1 ・熱膨張:遅延なしの線形応答(詳細化の優先度低) ・analogy:雪氷の融解量level1∝年平均の代表温度上昇量dTの積算温度(n次変化の場合、n+1次関数) ・dTの積算温度sum_dTの漸化式(feedback項を含む) 陽解法:sum_dT=(1-1/Tc)*sum_dT+b*dT 陰解法:sum_dT=(sum_dT+b*dT)/(1+1/Tc) ・無次元の重み係数b:総spotの形状因子 定数の場合、漸化式から外出可:k1*b ・時定数 通常mode:Tc=Order(100年) 暴走mode:Tc→+∞(緩和なし) ・海面上昇level:level0+level1 level0:k0*dT(線形項) level1:k1*sum_dT(非線形項) ・残存量の制限:level1≤level1max level:level0+min(level1max,level1) ・回帰直線の線膨張量係数k0/k1:基準年の実測値に適合(rate||寄与度換算) 実施例 ・西暦2000年の海面上昇の適合結果(寄与度換算) level0の線膨張量係数[cm/℃]:k0=11.46953405017921 level1の線膨張量係数[cm/℃]:k1=0.18059344991172854 時定数[年]:Tc=500(仮) 重み係数:b=1(基準年) ・最終氷期⇒間氷期の海面上昇の適合結果 温度peakの推定時刻[年]:tpeak=-7700 温度上昇rate[℃/年]:rateT=7/(1.8e4-7700) 時定数[年]:Tc=900 重み係数:b=10.5 ・氷期の形状因子bが10.5倍の結論 b=1の未来予測:単なる適合で定量性はないが、未来のlevelを過小評価の可能性あり b安全率の検討:step応答の2桁差の内1桁の幾分かを説明する候補 ・modelling詳細化の検討候補 氷期と現在で異なる状況:駆動力とrate||日射と氷床分布 Tc:熱輸送の時間遅れの実質寄与度と現在の経過時間(正味予測) k0:海水温と熱膨張率の整合性||水深方向の熱容量と時間遅れの考慮(非線形化) k1:analogyの見直し||形状因子bの時間変化(Tcとk1に従属) ・補足 全海洋平均の水深[km]:0.97*1.4e9/0.36e9=3.772222222222222 水深0~2kmの平均温度[℃]:20~2 20℃の熱膨張率[1/℃]:0.025e-2 水深2kmまで+[1,2]℃の熱膨張量[cm]:2e5*0.025e-2*[1,2]=[50,100](熱膨張率と海洋面積一定を仮定) |
|
目次
0D-cell simplified modelling |
電気化学cellを漸化式で記述する0D-cellのsimplified modellingについて記述する
simplifiedの仮定を列挙する ・負極||電解質||正極の影響は合成して区別しない ・電解質/活物質界面の被膜抵抗は反応抵抗に合成して区別しない ・電荷移動律速過程におけるButler-Volmer式の非線形性は考慮しない ・拡散律速過程における拡散抵抗の非線形性は考慮しない ・限界電流密度は考慮しない plot2d_EIS||plot2d_EIS_DFT||plot2d_IVに示す0D-cellの等価回路要素(直列接続)を列挙する ・構造由来のinductance: L ・導電path上の電子伝導とion伝導を合成する直流抵抗: R0 ・RC並列回路で表すion挿入/脱離||還元/酸化の反応抵抗: R1,C1 -> a1,b1 ・ion濃度分布緩和過程の電位変化に伴う拡散抵抗(Warburg's Zの代替): a2,b2 実施例は0D-cell EIS simulation参照 |
|
目次
0D-heat simplified modelling |
熱収支を漸化式で記述する0D-heatのsimplified modellingについて記述する
地球の対流圏と成層圏の熱収支のmodellingを一例に示す ※最も単純化した参考程度(前提から正しいとは限らない) ・energy保存則はthermodynamics laws ・地球表面と擬似的な対流圏界面における熱流束はNewton's law of cooling ・地球表面の黒体放射温度はStefan-Boltzmann's law ・Ver.2.95.32以降、albedoと独立に定義する対流圏の吸収率=1-成層圏への透過率を追加考慮 ・Ver.2.96.32以降、 ・Ver.2.96.32以降、擬似的な熱伝達係数の定義文を訂正 ・Ver.2.97.32以降、地球表面の熱伝達係数alpha0を追加考慮(最悪想定の場合、alpha0=0) ・Ver.2.97.32以降、対流圏の吸収率基準値を黒体放射温度から一意に決定 ・Ver.2.99.32以降、energy保存則の省略項を訂正 ・Ver.2.507.90以降、太陽定数の補足を追記 ・Ver.2.523.90以降、放射強制力の厳密な定義を追記 ・Ver.2.530.91以降、大気の吸収率の定義文を訂正(半値幅 ⇒ 半分値) ・Ver.2.597.93以降、陰解法の導出式の説明文を簡略化 ・Ver.2.614.95以降、時定数の表記を修正:O(年) ⇒ Order(1年) ・Ver.2.621.97以降、時定数を修正:Order(1年) ⇒ Order(0.1~1年) 前提を列挙する ・放射強制力(気候変動の統一指標):対流圏界面の熱流束fluxの変化量(系内部の増加が正) ・対流圏を系内部、成層圏と地球内部を系外部と想定する ・系外部の状態は変化しないと仮定する ・系内部の状態分布は一定を仮定する(温度・密度・圧力・吸収率等の分布は考慮しない) ・系内部の物性値は一定を仮定する(圧力・温度依存性等は考慮しない) ・系内部は準静的な定圧状態を仮定する ・系内外相互の非状態量の仕事=0(対流圏は十分に発達済み)を仮定する ・太陽活動||公転軌道等、系外部の大局的な変化は定常状態を仮定する ・大気・海洋循環||火山活動等、系内部と地球内部で循環する因子は系全体で定常状態を仮定する ・粘性による散逸||相変化による潜熱等、系内部で循環する局所的な因子は系全体で定常状態を仮定する ・地球内部と対流圏、成層圏の各温度を一意な代表値で表す ・対流圏の正味熱収支を次の一意な代表値で表す 放射強制力による放熱電力 対流圏の正味発熱電力=直接反射と成層圏への透過を除く太陽放射の放射電力 地球表面から対流圏への熱伝達電力 ・放射強制力を対流圏と成層圏の代表温度差の比例係数(擬似的な熱伝達係数)に換算する ※擬似的な熱伝達係数は対流圏の吸収率基準値に従属する透過による放射を含まない 主要なparameterを列挙する ・透過による放射を含まない擬似的な熱伝達係数alpha1 ・地球表面の熱伝達係数alpha0 ・太陽放射の直接反射率albedo ・albedoと独立に定義する対流圏の吸収率absorb ※対流圏の吸収率absorb=1-成層圏への透過率 ※対流圏の正味吸収率absorbe=(1-albedo)*absorb ※その他の全因子は定常状態(系内部のenergy変化に寄与しない)を想定する 代表的な状態量||物性値を示す 太陽定数(太陽放射の強度)I0=1367[W/m^2] Stefan-Boltzmann定数sigma=5.670374419184429e-8[W/m^2K^-4] Kelvin温度TK=273.15[K] 成層圏---------------系外部を想定 成層圏代表温度T1=-56.5[℃] 対流圏界面-----------放射強制力の熱流束flux1=alpha1*(T1-T)[W/m^2] 放射強制力から換算する擬似的な熱伝達係数alpha1[W/m^2K] 対流圏平均高度H1=11000[m] 対流圏界面半径R1=R0+H1=6389136.6[m] 太陽に対する地球表面の投影面積S0=pi*R0^2=127801957318946.73[m^2] 太陽に対する対流圏界面の投影面積S1=pi*R1^2=128243162607552.88[m^2] 対流圏界面面積A1=S1*4=512972650430211.5[m^2] 放射強制力による放熱電力W1=flux1*A1=alpha1*A1*(T1-T)[W] 対流圏---------------系内部を想定 対流圏代表温度T[℃] 対流圏代表温度変化量dT=T-T0[℃] 太陽放射の直接反射率基準値albedo0=0.3 大気の吸収率半分値absorbh=0.3859311811416972 対流圏の吸収率基準値absorb0=0.6284819702443666 対流圏の正味吸収率absorbe=(1-albedo)*absorb ※各基準値は温度変化の時定数に影響するが、熱平衡状態前後の温度変化量に影響しない 太陽放射の放射電力W0=S1*I0=175308403284524770[W] 太陽放射の直接反射による放射電力W0a=W0*albedo[W] 対流圏から成層圏への透過による放射電力W0t=W0*(1-albedo)*(1-absorb)[W] 対流圏の正味発熱電力W0e=W0*(1-albedo)*absorb[W] 大気の熱伝導率l=0.0241[W/(m*K)] 大気の密度rho=1.29[kg/m^3] 大気の定圧比熱cp=1007[J/(kg*K)] 対流圏の体積V=_ir(=<4*pi*r^2,R0,R0+H1)=5632989850743111000+O(1e+8)[m^3] 対流圏の熱容量C=rho*cp*V=7.317422805810823e+21+O(2e+11)[J/K] 地球表面-------------対流圏への熱流束flux0=alpha0*(T0-T)[W/m^2] 地球表面の熱伝達係数alpha0 地球表面温度T0=T1+6.5*H1/1e3=15[℃] 赤道半径R0=6378136.6[m] 地球表面積A0=S0*4=511207829275786.94[m^2] 対流圏への熱伝達電力W2=flux0*A0=alpha0*A0*(T0-T)[W] 黒体放射温度Te=(I0*(1-albedo0)/(4*e0*sigma))**0.25-TK=-18.291744141682386[℃] 対流圏のenergy保存則 ・総電力の保存 W0=W0a+W0t+W0e ・直接反射W0aと透過W0tを除く対流圏の正味熱収支 Q'=W1+W0e+W2 ・系内部の対流圏が系外部に与える仕事は十分に小さい(-V*p'/Q'=0)と仮定する C*T'-V*p'=Q' -> C*T'=W1+W0e+W2 ・T'=0の熱平衡状態における正味熱収支に熱容量Cは寄与しない C*T'=alpha1*A1*(T1-T)+W0*(1-albedo)*absorb+alpha0*A0*(T0-T) ・非平衡状態の時間発展方程式を得る T'=-a*T+b a=(alpha1*A1+alpha0*A0)/C b=(alpha1*A1*T1+W0*(1-albedo)*absorb+alpha0*A0*T0)/C ・時間微分T'を陰解法で離散化して次の漸化式を得る newT=(oldT+b*dt)/(1+a*dt) dT=newT-T0 test caseを示す kalpha0=0; kalpha1=1; kalbedo=1; kabsorb=1; I0=1367; sigma=5.670374419184429e-8; TK=273.15; T0=15; T1=-56.5; T0K=T0+TK; T1K=T1+TK; H1=11000; R0=6378136.6; R1=R0+H1; S0=pi*R0^2; S1=pi*R1^2; A0=S0*4; A1=S1*4; albedo0=0.3; e0=1; TeK=(I0*(1-albedo0)/(4*e0*sigma))**0.25; Te=TeK-TK; W0=S1*I0; Wee=A0*(e0*sigma*TeK**4); We0=A0*(e0*sigma*T0K**4); absorbh=1-W0*(1-albedo0)/We0; absorbhmax=0.5; absorb0=We0*absorbh/(W0*(1-albedo0)); absorb0max=We0*absorbhmax/(W0*(1-albedo0)); kh0=(absorbhmax-absorbh)/(absorb0max-absorb0); Te_th(a)=<(I0*(1-albedo0)/(2*(2-a)*e0*sigma))**0.25-TK; Te_th0=Te_th(absorbh*2)=>; Wea=We0*absorbh; Wet=We0*(1-absorbh); l=0.0241; rho=1.29; cp=1007; V=_ir(=<4*pi*r^2,R0,R0+H1); C=rho*cp*V; alpha10=-W0*(1-albedo0)*absorb0/(A1*(T1-T0)); alpha0=alpha10*kalpha0; alpha1=alpha10*kalpha1; albedo=albedo0*kalbedo; absorb=absorb0*kabsorb; absorbe=(1-albedo)*absorb; T=T0; flux0=alpha0*(T0-T); flux1=alpha1*(T1-T); W2=flux0*A0; W1=flux1*A1; W0a=W0*albedo; W0t=W0*(1-albedo)*(1-absorb); W0e=W0*(1-albedo)*absorb; (Wee-Wet); (Wea-W0e); (W0t+W0e-Wet); (W0a+W0t+W0e-W0); (W1+W0e+W2); ・地球表面の黒体放射温度(輻射率e0=1) A0*(e0*sigma*TeK**4)=S0*I0*(1-albedo0) -> TeK=(I0*(1-albedo0)/(4*e0*sigma))**0.25; Te=TeK-TK; Te -> -18.291744141682386 ・総電力 We0=A0*(e0*sigma*T0K**4); We0 -> 199840601786823800 W0=S1*I0; W0 -> 175308403284524770 ・大気の吸収率半分値 We0*(1-absorbh)=W0*(1-albedo0) -> absorbh=1-W0*(1-albedo0)/We0; absorbh -> 0.3859311811416972 ・対流圏の吸収率に換算 We0*absorbh=W0*(1-albedo0)*absorb0 -> absorb0=We0*absorbh/(W0*(1-albedo0)); absorb0 -> 0.6284819702443666 ・absorbh=absorbhmax=0.5の場合、対流圏の吸収率上限値 absorb0max=We0*absorbhmax/(W0*(1-albedo0)); absorb0max -> 0.8142409851221832 ・大気の吸収率半分値への換算係数 kh0 -> 0.6140688188583029 ・大気の熱拡散係数D_l=O(1e-5) D_l=l/(rho*cp); D_l -> 0.000018552304411753384 ・大気の熱拡散の時定数Tc_l=Order(1万年) Tc_l=H1^2/D_l; Tc_l -> 6522100829875.518 ・よって熱拡散は対流圏で支配しない s_1year=60*60*24*365; s_1year -> 31536000 year_l=Tc_l/s_1year; year_l -> 206814.46061249104 ・T'=0の熱平衡状態における放射強制力を擬似的な熱伝達係数基準値alpha10に換算する alpha10=-W0*(1-albedo0)*absorb0/(A1*(T1-T0)); alpha10 -> 2.1027776130308893 ・放射強制力の時定数Tc_a=Order(0.1~1年) Tc_a=C/(alpha10*A1); Tc_a -> 6783761.861191721+O(2e-4) ・よって対流||放射による熱輸送が対流圏で支配する(対流圏は十分に発達済みの一例) year_a=Tc_a/s_1year; year_a -> 0.21511167748578514+O(6e-12) ・以上より、T'=0の熱平衡状態における漸化式の各係数を求める a=alpha10*A1/C; a -> 1.4741083494112034e-7+O(4e-18) b=(alpha10*A1*T1+W0*(1-albedo0)*absorb0)/C; b -> 0.0000022111625241168055+O(6e-17) ・熱平衡状態(放熱電力W1+正味発熱電力W0e+熱伝達電力W2=0)のdouble-checkを示す flux1=alpha10*(T1-T0); flux1 -> -150.34859933170858 W1=flux1*A1; W1 -> -77124719487656480 W0e -> 77124719487656480 W2 -> 0 W1+W0e+W2 -> 0 ・absorb0=absorb0max=0.8142409851221832の場合、alpha10は増加する alpha10 -> 2.724290904417542 Tc_a -> 5236130.455347437+O(1e-4) year_a -> 0.16603660753892177+O(4e-12) a -> 1.9098072680346273e-7+O(5e-18) b -> 0.00000286471090205194+O(7e-17) flux1 -> -194.78679966585426 ・同時に、放射強制力による放熱電力W1の増加分、透過による放射電力W0tが減少する W1 -> -99920300893411890 W0e -> 99920300893411890 W2 -> 0 W1+W0e+W2 -> 0 ・absorb0=0.5の場合、alpha10は減少する alpha10 -> 1.6729020979020977 Tc_a -> 8526944.040380726+O(2e-4) year_a -> 0.27038762177767395+O(7e-12) a -> 1.1727530933290258e-7+O(3e-18) b -> 0.0000017591296399935375+O(5e-17) flux1 -> -119.61249999999998 ・同時に、放射強制力による放熱電力W1の減少分、透過による放射電力W0tが増加する W1 -> -61357941149583660 W0e -> 61357941149583660 W2 -> 0 W1+W0e+W2 -> 0 実施例は0D-heat simulation参照 |
|
目次
simulation |
simulationの実施例を列挙する
・EIS simulation ・0D-cell EIS simulation ・0D-heat simulation |
|
目次
EIS simulation |
EIS simulationの実施例について記述する
Electrochemical Impedance Spectroscopy(以降、EISと省略する) のsimulationの背景と目的を列挙する ・等価回路fittingによる電気化学cellのsimulationは交流impedance実測結果の再現性が低い ・測定機の後処理同等(noise処理を除く)のalgorithmを実装することで再現性を改善する ・定性的な理解とともにparameter推定の定量性改善に繋がる可能性が考えられる plot2d_EISに示すZ変換(impedance演算部)の想定algorithmを列挙する ・電流Iと電圧Vは正の相関を前提とする ・各実測波形の角周波数をomegaとして時間tに対する基準波形exp(-i*omega*t)を作る ・得られた複素数の基準波形を各実測波形に時間領域で乗算する ・さらに、得られた複素数の各波形を合成Simpson公式で時間積分する(式変数FT_IV) ・最後に、得られた各複素数の比からZ=zV/zIに変換する(式変数calc_Z) ・仮に、RC並列回路のcut-off周波数で Zが複素数平面の第4象限(半円の頂点で位相が負)に位置しない場合、基準波形を見直す Ver.2.64.27以降、想定algorithmの補足を列挙する ・基準波形を含む時間積分は周期関数の連続Fourier変換||Laplace変換に同義 ・Laplace領域||波数領域の変数s=i*omegaを定義して各実測波形を連続Fourier変換する I(s)=FT(I(t)) V(s)=FT(V(t)) Z(s)=V(s)/I(s) ・以上より、時間領域から波数領域のZ(s)に変換する Ver.2.64.27以降、plot2d_EIS_DFTに示す hard/softの制約を考慮する場合、plot2d_EISの変化点を列挙する ・時間tに対する電流波形I(t)と電圧波形V(t)のsampling時刻/sampling間隔が同一を前提とする ・各実測波形の連続Fourier変換を離散Fourier変換で代替する I(s)=DFT(I(t)) V(s)=DFT(V(t)) Z(s)=V(s)/I(s) ・以上より、時間領域から波数領域のZ(s)に変換する(高精度の時間積分は不要) Ver.2.64.27以降、想定algorithmの数値誤差について補足を列挙する ・時間積分に換算してZ変換の数値誤差を示す 連続Fourier変換の場合、合成Simpson公式のOrder(dt^4) 離散Fourier変換の場合、台形公式より低次のOrder(dt) ・I(t)||V(t)のmodelling誤差がOrder(dt)の場合、Z変換の数値誤差は同等以下で支配しない ・実測結果も同様に、影響は小さいと考えられるが、より厳密には Z変換のalgorithmを統一する||Z変換前の波形を比較する 電気化学cellの交流impedance測定における留意事項を列挙する(参考) ・Open Circuit Voltage測定中に測定対象は測定機の影響(主に暗電流)を受けて変化しない ・測定電流||電圧の入力と測定対象の応答がButler-Volmer式の線形領域の範囲内に収まる ・測定機と測定対象の接続線impedance(主にinductance)を分離できる |
|
目次
0D-cell EIS simulation |
0D-cell EIS simulationの実施例について記述する
0D-cellのEIS simulationの実施例を示す ・plot2d_EIS測定条件 電流振幅dI=1e-3 sweep開始周波数f0=1e3 sweep終了周波数f1=0.01 sweep周波数分割数Nf=10 積分1周期分割数Nt=100 積分周回数Nint=1 ・各parameterの設定値 L=1e-4, R0=1, R1=2,C1=0.1, -> 1/(2pi*R1*C1)=0.7957747154594768(cut-off周波数≒1) a1=1/(R1*C1),b1=1/C1, -> 1/a1=0.2(時定数=0.2) a2=0.01,b2=0.12, -> 1/a2=100(有効拡散の時定数=100) ・時間発展の解法の設定値(陰解法選択) isImplicit=1, ・logarithmic-scale等分割の周波数に対するZのsimulation結果 ( 999.9999999999998,infoLost[ri] 1.000054390110971+0.626708495177503i: 316.22776601683796,infoLost[ri] 1.000197769963539+0.1936010152622332i: 100.00000000000004,infoLost[ri] 1.0008791279248923+0.046741593442684845i: 31.62277660168379,infoLost[ri] 1.0051946423727691-0.030877367568292336i: 10.00000000000001,infoLost[ri] 1.0370746940376958-0.15139417727049678i: 3.162277660168381,infoLost[ri] 1.2428463848394768-0.4426585101482536i: 1,infoLost[ri] 1.9692074050771464-0.8189304441759584i: 0.3162277660168378,infoLost[ri] 2.7478680202043564-0.6543142174993192i: 0.10000000000000024,infoLost[ri] 2.978079231896037-0.42406164035890753i: 0.031622776601683854,infoLost[ri] 3.0951852485694045-0.675153482065019i: 0.010000000000000012,infoLost[ri] 3.711459875093761-1.811702692783572i ) ・Nyquist-plot(real(Z),-imag(Z)) ( infoLost[ri] 1.000054390110971,infoLost[ri] -0.626708495177503: infoLost[ri] 1.000197769963539,infoLost[ri] -0.1936010152622332: infoLost[ri] 1.0008791279248923,infoLost[ri] -0.046741593442684845: infoLost[ri] 1.0051946423727691,infoLost[ri] 0.030877367568292336: infoLost[ri] 1.0370746940376958,infoLost[ri] 0.15139417727049678: infoLost[ri] 1.2428463848394768,infoLost[ri] 0.4426585101482536: infoLost[ri] 1.9692074050771464,infoLost[ri] 0.8189304441759584: infoLost[ri] 2.7478680202043564,infoLost[ri] 0.6543142174993192: infoLost[ri] 2.978079231896037,infoLost[ri] 0.42406164035890753: infoLost[ri] 3.0951852485694045,infoLost[ri] 0.675153482065019: infoLost[ri] 3.711459875093761,infoLost[ri] 1.811702692783572 ) ・Bode-plot(log10(f),|Z|) ( 3,infoLost[ri] 1.1802001190933158: 2.5,infoLost[ri] 1.018762451286169: 2,infoLost[ri] 1.0019699622609723: 1.5,infoLost[ri] 1.005668772948065: 1.0000000000000004,infoLost[ri] 1.0480668480229642: 0.5000000000000002,infoLost[ri] 1.3193231950190327: 0,infoLost[ri] 2.13270365419317: -0.5000000000000002,infoLost[ri] 2.8246956918725874: -0.9999999999999989,infoLost[ri] 3.008119709432186: -1.4999999999999991,infoLost[ri] 3.1679652692708244: -1.9999999999999993,infoLost[ri] 4.130036446748411 ) ・Bode-plot(log10(f),deg_phi) ( 3,infoLost[ri] 32.07431944473854: 2.5,infoLost[ri] 10.954854996909933: 2,infoLost[ri] 2.6738010400823766: 1.5,infoLost[ri] -1.7594470164364941: 1.0000000000000004,infoLost[ri] -8.305482098595858: 0.5000000000000002,infoLost[ri] -19.604124709935633: 0,infoLost[ri] -22.58086538727024: -0.5000000000000002,infoLost[ri] -13.393680249677557: -0.9999999999999989,infoLost[ri] -8.104114612346955: -1.4999999999999991,infoLost[ri] -12.305194523809629: -1.9999999999999993,infoLost[ri] -26.018737805525532 ) 電流振幅のみ変更dI=1の影響 ・線形modelを前提とするため、Zのsimulation結果はほぼ一致 ( 999.9999999999998,infoLost[ri] 1.0000543901109709+0.626708495177503i: 316.22776601683796,infoLost[ri] 1.0001977699635385+0.19360101526223303i: 100.00000000000004,infoLost[ri] 1.000879127924892+0.04674159344268477i: 31.62277660168379,infoLost[ri] 1.005194642372769-0.030877367568292353i: 10.00000000000001,infoLost[ri] 1.0370746940376954-0.15139417727049667i: 3.162277660168381,infoLost[ri] 1.2428463848394775-0.44265851014825364i: 1,infoLost[ri] 1.9692074050771455-0.818930444175958i: 0.3162277660168378,infoLost[ri] 2.7478680202043564-0.6543142174993192i: 0.10000000000000024,infoLost[ri] 2.978079231896035-0.42406164035890764i: 0.031622776601683854,infoLost[ri] 3.095185248569406-0.6751534820650186i: 0.010000000000000012,infoLost[ri] 3.71145987509376-1.8117026927835727i ) 1周期分割数のみ変更Nt=300の影響 ・Zのsimulation結果はmodelling誤差のOrder(dt)で定量的に大差なし ( 999.9999999999998,infoLost[ri] 1.000020659557588+0.6267079711134935i: 316.22776601683796,infoLost[ri] 1.0000911276222495+0.19359899557421248i: 100.00000000000004,infoLost[ri] 1.0005422375176036+0.04673158634642843i: 31.62277660168379,infoLost[ri] 1.0041360205082939-0.03094497386189218i: 10.00000000000001,infoLost[ri] 1.0338770846371845-0.15195130473296967i: 3.162277660168381,infoLost[ri] 1.2354229873663194-0.44693493528151573i: 1,infoLost[ri] 1.9658931475663823-0.834774843093126i: 0.3162277660168378,infoLost[ri] 2.754521803915976-0.6657796106753855i: 0.10000000000000024,infoLost[ri] 2.9786451872376074-0.42699666778887413i: 0.031622776601683854,infoLost[ri] 3.0844475430285048-0.6771795132687214i: 0.010000000000000012,infoLost[ri] 3.678381237481611-1.8236767191289074i ) 積分周回数のみ変更Nint=3の影響 ・Zのsimulation結果は定性的に大差なし ( 999.9999999999998,infoLost[ri] 1.0000543775353226+0.6267084951674945i: 316.22776601683796,infoLost[ri] 1.0001973780496354+0.1936010142760755i: 100.00000000000004,infoLost[ri] 1.000867290892417+0.04674149927015193i: 31.62277660168379,infoLost[ri] 1.004870193211877-0.03088552575238536i: 10.00000000000001,infoLost[ri] 1.0304047344117009-0.1519236330216015i: 3.162277660168381,infoLost[ri] 1.1783944036609526-0.4587506996017625i: 1,infoLost[ri] 1.845520769797103-0.9149750525109858i: 0.3162277660168378,infoLost[ri] 2.725785909977971-0.7058617623925021i: 0.10000000000000024,infoLost[ri] 2.976327232225026-0.4319501793746518i: 0.031622776601683854,infoLost[ri] 3.0824015886720364-0.6769040880523296i: 0.010000000000000012,infoLost[ri] 3.5317647358815623-1.8403531943834652i ) 時間発展の解法のみ変更isImplicit=0(陽解法選択)の影響 ・陽解法の安定条件 dt≤min(0.2,100)*2 1/(f*Nt)≤0.4 f≥0.025 ・Zのsimulation結果は陽解法の安定条件の範囲内で定性的に大差なし ( 999.9999999999998,infoLost[ri] 1.0000543929898555+0.626708415628734i: 316.22776601683796,infoLost[ri] 1.0001978068781259+0.19360021990102563i: 100.00000000000004,infoLost[ri] 1.0008797482133391+0.04673364653178407i: 31.62277660168379,infoLost[ri] 1.0052082296658387-0.03095637279042429i: 10.00000000000001,infoLost[ri] 1.0373952733381435-0.15214941818882316i: 3.162277660168381,infoLost[ri] 1.2486473969330358-0.4481778175693221i: 1,infoLost[ri] 2.012036843642123-0.8250361448914947i: 0.3162277660168378,infoLost[ri] 2.8088203160184415-0.5898729668672302i: 0.10000000000000024,infoLost[ri] 3.003399673907799-0.3117472516446023i: 0.031622776601683854,infoLost[ri] 3.1017196891639354-0.5529342786020476i: 0.010000000000000012,infoLost[ri] -6.24810011909696e+55-7.398061071461481e+55i ) 連続Fourier変換を離散Fourier変換で代替の影響(Ver.2.64.27追記) ・plot2d_EIS_DFTに示すZのsimulation結果は定性的に大差なし ( 999.9999999999998,infoLost[ri] 1.0000543892797595+0.6392747864438679i: 316.22776601683796,infoLost[ri] 1.0001977616975484+0.19757406150509768i: 100.00000000000004,infoLost[ri] 1.0008790467041697+0.04799047769435572i: 31.62277660168379,infoLost[ri] 1.0051938738253914-0.030553331468587727i: 10.00000000000001,infoLost[ri] 1.0370682220140526-0.15188583273656356i: 3.162277660168381,infoLost[ri] 1.2428077197277516-0.4463003704640858i: 1,infoLost[ri] 1.9691091944331642-0.8282224753004641i: 0.3162277660168378,infoLost[ri] 2.747797860771646-0.6608797016283408i: 0.10000000000000024,infoLost[ri] 2.9780526592821848-0.42653152705817254i: 0.031622776601683854,infoLost[ri] 3.095161552636316-0.6774520967840967i: 0.010000000000000012,infoLost[ri] 3.71133683621205-1.8234973547405815i ) |
|
目次
0D-heat simulation |
0D-heat simulationの実施例について記述する
heat0d_evolutionよりParis協定努力目標(温度上昇量<1.5℃)を満たす必要条件を示す ※系内部の対流圏を最も単純化した参考程度(前提から正しいとは限らない) ※擬似的な熱伝達係数の変化率kalpha1=(100-放射強制力の増加割合)/100 ・Ver.2.95.32以降、albedoと独立に定義する対流圏の吸収率=1-成層圏への透過率を追加考慮 ・Ver.2.96.32以降、対流圏の吸収率基準値absorb0=0.5~1の前提で必要条件を範囲に修正 ※対流圏の吸収率absorb=1-成層圏への透過率 ※対流圏の正味吸収率absorbe=(1-albedo)*absorb ・Ver.2.97.32以降、地球表面の熱伝達係数alpha0を追加考慮(最悪想定の場合、alpha0=0) ・Ver.2.97.32以降、対流圏の吸収率基準値を黒体放射温度から一意に決定して範囲を修正 ・Ver.2.102.32以降、大気の吸収率について補足を追記 ・Ver.2.614.95以降、時定数の表記を修正:感度O(年) ⇒ 1次感度Order(1年) ・Ver.2.621.97以降、時定数を修正:Order(1年) ⇒ Order(0.1~1年) 放射強制力の増加量<基準値の約2%=3.007~3.896[W/m^2] ・基準値flux1=alpha10*(T1-T0)=2.1027776130308893*(-56.5-15)=-150.3[W/m^2] ・基準値absorb0=0.6284819702443666 heat0d_evolution[1](s_1day*365*2,s_1day,0,0.98,1,1)=> -> 1.4590132585988513+O(4e-15) heat0d_evolution[1](s_1day*365*2,s_1day,0,0.97,1,1)=> -> 2.211057108488781+O(4e-15) ・基準値flux1=alpha10*(T1-T0)=2.724290904417542*(-56.5-15)=-194.8[W/m^2] ・基準値absorb0=absorb0max=0.8142409851221832 heat0d_evolution[1](s_1day*365*2,s_1day,0,0.98,1,1)=> -> 1.4591716940508412+O(4e-15) heat0d_evolution[1](s_1day*365*2,s_1day,0,0.97,1,1)=> -> 2.2113197668795657 ・基準値flux1=alpha10*(T1-T0)=1.6729020979020977*(-56.5-15)=-119.6[W/m^2] ・基準値absorb0=0.5(温度変化の時定数がabsorb0=1の2倍) heat0d_evolution[1](s_1day*365*2,s_1day,0,0.98,1,1)=> -> 1.4581084444178032+O(4e-15) heat0d_evolution[1](s_1day*365*2,s_1day,0,0.97,1,1)=> -> 2.2095869064056366 ・基準値flux1=alpha10*(T1-T0)=3.3458041958041953*(-56.5-15)=-239.2[W/m^2] ・基準値absorb0=1 heat0d_evolution[1](s_1day*365,s_1day,0,0.98,1,1)=> -> 1.45806982458949+O(4e-15) heat0d_evolution[1](s_1day*365,s_1day,0,0.97,1,1)=> -> 2.2095252201233+O(4e-15) albedoの低下量<基準値の約5%=0.015 ・基準値albedo0=0.3 ・基準値absorb0=0.5(温度変化の時定数がabsorb0=1の2倍) heat0d_evolution[1](s_1day*365*2,s_1day,0,1,0.96,1)=> -> 1.2249341490778392 heat0d_evolution[1](s_1day*365*2,s_1day,0,1,0.95,1)=> -> 1.531167686347434+O(4e-15) ・基準値albedo0=0.3 ・基準値absorb0=1 heat0d_evolution[1](s_1day*365,s_1day,0,1,0.96,1)=> -> 1.224904963446054+O(4e-15) heat0d_evolution[1](s_1day*365,s_1day,0,1,0.95,1)=> -> 1.5311312043076661+O(4e-15) 対流圏の吸収率の増加量<基準値の約2%=0.01257~0.01628 ・基準値absorb0=0.6284819702443666 heat0d_evolution[1](s_1day*365*2,s_1day,0,1,1,1.02)=> -> 1.4298610104595788 heat0d_evolution[1](s_1day*365*2,s_1day,0,1,1,1.03)=> -> 2.1447915156892385 ・基準値absorb0=absorb0max=0.8142409851221832 heat0d_evolution[1](s_1day*365*2,s_1day,0,1,1,1.02)=> -> 1.4299907377329752+O(4e-15) heat0d_evolution[1](s_1day*365*2,s_1day,0,1,1,1.03)=> -> 2.144986106599564+O(4e-15) ・基準値absorb0=0.5(温度変化の時定数がabsorb0=1の2倍) heat0d_evolution[1](s_1day*365*2,s_1day,0,1,1,1.02)=> -> 1.4290898405909296 heat0d_evolution[1](s_1day*365*2,s_1day,0,1,1,1.03)=> -> 2.1436347608863073 ・基準値absorb0=1 heat0d_evolution[1](s_1day*365,s_1day,0,1,1,1.02)=> -> 1.42905579068713+O(4e-15) heat0d_evolution[1](s_1day*365,s_1day,0,1,1,1.03)=> -> 2.1435836860307056 Ver.2.102.32以降、大気の吸収率について補足を列挙する ・大気の吸収率基準値a0 a0=absorbh*2; a0 -> 0.7718623622833944 ・大気の吸収率上限値amax amax=absorbhmax*2; amax -> 1 ・対流圏の吸収率から次の必要条件が得られる 大気の吸収率の増加量<基準値の約2.5%=0.01896~0.02456 (kh0*2)*2 -> 2.4562752754332116[%] ・大気の吸収率aを考慮して地球表面の黒体放射温度の理論値を式変数Te_thで定義する Te_th(a)=<(I0*(1-albedo0)/(2*(2-a)*e0*sigma))**0.25-TK; ・大気の吸収率基準値における黒体放射温度の理論値Te_th0を示す Te_th0=Te_th(a0)=>; Te_th0 -> 14.751843195026424[℃] ・理論値から次の必要条件(上記の緩和側)が得られる 大気の吸収率の増加量理論値<基準値の約3.3%=0.02526 Te_th(a0+0.01)=>-Te_th0 -> 0.5890544664107438 Te_th(a0+0.02)=>-Te_th0 -> 1.1841847856840104 Te_th(a0+0.03)=>-Te_th0 -> 1.7855047027240971 Te_th(a0+0.025264986)=>-Te_th0 -> 1.500000016245508 ・百分率に換算 (0.025264986/a0)*100 -> 3.2732501589090033[%] ※以上の条件はほぼ等価で基準値に応じて右辺の絶対量は変化する 放射強制力の増加割合=2%が即座に反映された場合、年間30日毎の温度変化を示す ※放射強制力のtotal増加割合=2% ・実行文 heat0d_evolution[1](s_1day*30,s_1day,0,0.98,1,1)=> ・年間30日毎の温度変化量dT[℃] 0 0.4534194999132346+O(3e-13) 0.7659456725233014+O(2e-13) 0.9813590117929607+O(2e-13) 1.1298358780591116+O(1e-13) 1.2321757790650807+O(7e-14) 1.3027150866440742+O(5e-14) 1.3513353595270061+O(4e-14) 1.3848476098785376+O(2e-14) 1.4079464297129753+O(2e-14) 1.4238676367983416+O(1e-14) 1.434841566932981+O(1e-14) 1.442405512427431+O(7e-15) ・対策効果の1次感度に相当する放射強制力の時定数Tc_a=Order(0.1~1年) 以降、記述がない限り、対流圏の吸収率基準値absorb0=1とする 放射強制力の増加割合=2%が即座に反映された場合、年間30日毎の温度変化を示す ※放射強制力のtotal増加割合=2% ・実行文 heat0d_evolution[1](s_1day*30,s_1day,0,0.98,1,1)=> ・年間30日毎の温度変化量dT[℃] 0 0.6502836201909368+O(4e-13) 1.0107690509029403+O(2e-13) 1.2106045407119588+O(1e-13) 1.3213835614017384+O(7e-14) 1.3827940317677054+O(4e-14) 1.4168369926739004+O(2e-14) 1.4357087450046429+O(7e-15) 1.4461703213937902+O(7e-15) 1.4519697076207692+O(4e-15) 1.4551846036707268 1.4569667847856707 1.4579547388212255 ・放射強制力の時定数はabsorbe0=(1-albedo0)*absorb0に反比例 さらに、対流圏の吸収率基準値absorb0=0.5の場合、2年間30日毎の温度変化を示す ※放射強制力のtotal増加割合=2% ・実行文 heat0d_evolution[1](s_1day*30,s_1day,0,0.98,1,1)=> ・2年間30日毎の温度変化量dT[℃] 0 0.3743263957803489+O(3e-13) 0.6526263261296812+O(2e-13) 0.8595335923698304+O(2e-13) 1.013362652870235+O(1e-13) 1.127729732791785+O(9e-14) 1.2127580683171963+O(7e-14) 1.2759739679202902+O(5e-14) 1.322973005804954+O(4e-14) 1.357915315824318+O(2e-14) 1.3838938269692704+O(2e-14) 1.4032080349004232+O(1e-14) 1.4175675424921579+O(1e-14) ・時定数が2倍 1.4282433858408403+O(1e-14) 1.4361805404039458+O(7e-15) 1.4420815657844344+O(7e-15) 1.4464687930034827+O(7e-15) 1.4497305587866585+O(4e-15) 1.4521555793048506+O(4e-15) 1.4539585059723876+O(4e-15) 1.4552989253808235+O(4e-15) 1.4562954851538166+O(4e-15) 1.4570363960768553+O(4e-15) 1.4575872401012226+O(4e-15) 1.4579967753499865+O(4e-15) ・基準値の違いは熱平衡状態前後の温度変化量に影響しない さらに、対流圏の吸収率基準値absorb0=0.5、 太陽放射の直接反射率基準値albedo0=0.65の場合、4年間30日毎の温度変化を示す ※放射強制力のtotal増加割合=2% ・実行文 heat0d_evolution[1](s_1day*30,s_1day,0,0.98,1,1)=> ・4年間30日毎の温度変化量dT[℃] 0 0.20146856235891342+O(2e-13) 0.3751204883635637+O(1e-13) 0.5247964033155164+O(1e-13) 0.6538066598219956+O(1e-13) 0.7650045522097688+O(9e-14) 0.8608494222714018+O(8e-14) 0.9434610520413074+O(7e-14) 1.014666546595727+O(5e-14) 1.0760407437742643+O(5e-14) 1.1289410445569423+O(4e-14) 1.1745374344332582+O(4e-14) 1.2138383597397961+O(3e-14) ・時定数が4倍 1.2477130312683826+O(3e-14) 1.2769106484292898+O(2e-14) 1.3020769691463947+O(2e-14) 1.3237685919574531+O(2e-14) 1.3424652661938836+O(1e-14) 1.358580502501848+O(1e-14) 1.3724707183753857+O(1e-14) 1.3844431209716959+O(1e-14) 1.3947625015510319+O(7e-15) 1.40365709181264+O(4e-15) 1.4113236116500936+O(7e-15) 1.4179316199663248+O(4e-15) 1.4236272647742751+O(4e-15) 1.4285365155236889 1.4327679491423773+O(7e-15) 1.4364151514107881+O(4e-15) 1.439558786780104+O(4e-15) 1.44226838241201 1.4446038658972107 1.446616890662014+O(4e-15) 1.44835197837698 1.449847503633947 1.4511365426692109 1.4522476049041835 1.4532052634825448+O(4e-15) 1.454030698749662+O(4e-15) 1.4547421666940785 1.4553554027116178+O(4e-15) 1.4558839696219863 1.4563395576349976 1.4567322429006033+O(4e-15) 1.4570707103611866+O(4e-15) 1.4573624458345975 1.4576139015766358+O(4e-15) 1.4578306389841842 1.4580174515956088+O(4e-15) ・基準値の違いは熱平衡状態前後の温度変化量に影響しない 対流圏の吸収率の増加割合=2%が即座に反映された場合、年間30日毎の温度変化を示す ※対流圏の吸収率のtotal増加割合=2% ・実行文 heat0d_evolution[1](s_1day*30,s_1day,0,1,1,1.02)=> ・年間30日毎の温度変化量dT[℃] 0 0.6466710687354009+O(4e-13) 1.0009061436670095+O(2e-13) 1.1949499077667447+O(1e-13) 1.3012436800400486+O(7e-14) 1.359469545099433+O(4e-14) 1.391364653245546+O(2e-14) 1.4088362343481045+O(1e-14) 1.4184068601890552+O(7e-15) 1.4236494812460734+O(7e-15) 1.426521297154899+O(4e-15) 1.4280944275651244+O(4e-15) 1.4289561608259724 さらに、対流圏の吸収率基準値absorb0=0.5の場合、2年間30日毎の温度変化を示す ※対流圏の吸収率のtotal増加割合=2% ・実行文 heat0d_evolution[1](s_1day*30,s_1day,0,1,1,1.02)=> ・2年間30日毎の温度変化量dT[℃] 0 0.3732199909517959+O(3e-13) 0.6490321765566822+O(2e-13) 0.8528593122203958+O(1e-13) 1.003488992130137+O(1e-13) 1.114805379890953+O(9e-14) 1.197068969586823+O(6e-14) 1.257862338162436+O(5e-14) 1.30278906305292+O(4e-14) 1.3359902272041566+O(2e-14) 1.3605261198979832+O(2e-14) 1.378658316333631+O(1e-14) 1.3920581364128815+O(1e-14) ・時定数が2倍 1.401960697241261+O(7e-15) 1.4092787590047742+O(4e-15) 1.414686857869583+O(4e-15) 1.418683480783745+O(4e-15) 1.421637013091022+O(4e-15) 1.4238196941388601 1.4254327107105276+O(7e-15) 1.426624741247032 1.4275056601569354+O(4e-15) 1.4281566653972035 1.4286377628263551+O(4e-15) 1.4289932971938697 ・基準値の違いは熱平衡状態前後の温度変化量に影響しない 放射強制力の年率増加割合=0.1%で徐々に変化した場合、20年間1年毎の温度変化を示す ※放射強制力のtotal増加割合=2% ・実行文 heat0d_evolution[1](s_1day*30*365*year,s_1day*30,0,1-0.001*year,1,1)=> ※本来、式変数内部のalpha1に変化量を反映するが、式変数のargumentsのkalpha1に反映 ・20年間1年毎の温度変化量dT[℃] 0 0.07157157157156036 0.14328657314629112 0.2151454363089229 0.28714859437751983 0.3592964824120557 0.4315895372233367 0.5040281973816736 0.5766129032258007 0.6493440968718538 0.7222222222222161 0.7952477249747183 0.8684210526315841 0.9417426545086087 1.0152129817444226 1.088832487309638 1.162601626016265 1.2365208545269724 1.3105906313645548 1.384811416921508 1.4591836734693757 さらに、alpha0=alpha10*0.1を想定する場合、20年間1年毎の温度変化を示す ※放射強制力のtotal増加割合=2% ・実行文 heat0d_evolution[1](s_1day*30*365*year,s_1day*30,0.1,1-0.001*year,1,1)=> ※本来、式変数内部のalpha1に変化量を反映するが、式変数のargumentsのkalpha1に反映 ・20年間1年毎の温度変化量dT[℃] 0 0.0650795175895933 0.13027761426015694 0.19559461439532555 0.261030843562958 0.32658662852060516 0.3922622972209435 0.4580581788171827 0.5239746036685791 0.5900119033460562 0.6561704106376478 0.7224504595541656 0.7888523853347547 0.855376524452593 0.9220232146205767 0.9887927947970176 1.0556856051914068 1.1227019872701511 1.1898422837623954 1.2571068386659334 1.3244959972530026 ・地球内部への放熱による温度の減少分、放射強制力の増加量に余裕が発生する さらに、alpha0=alpha10*1を想定する場合、20年間1年毎の温度変化を示す ※放射強制力のtotal増加割合=2% ・実行文 heat0d_evolution[1](s_1day*30*365*year,s_1day*30,1,1-0.001*year,1,1)=> ※本来、式変数内部のalpha1に変化量を反映するが、式変数のargumentsのkalpha1に反映 ・20年間1年毎の温度変化量dT[℃] 0 0.03582954841582797 0.07169502410910589 0.1075964811448511 0.14353397369660392 0.1795075560467243 0.2155172825866476 0.25156320781717767 0.2876453863487072 0.3237638729015764 0.359918722306265 0.39610998950376697 0.4323377295457771 0.4686019975949911 0.5049028489254237 0.5412403389226643 0.5776145230841614 0.6140254570195136 0.6504731964507151 0.6869577972124947 0.723479315252554 ・放射強制力同等の場合、地球内部の温度変化は想定しないため、温度上昇量は半減する さらに、放射強制力の年率増加割合を2倍に変更の場合、20年間1年毎の温度変化を示す ※放射強制力のtotal増加割合=4% ・実行文 heat0d_evolution[1](s_1day*30*365*year,s_1day*30,1,1-0.002*year,1,1)=> ※本来、式変数内部のalpha1に変化量を反映するが、式変数のargumentsのkalpha1に反映 ・20年間1年毎の温度変化量dT[℃] 0 0.07169502410910589 0.14353397369660392 0.2155172825866476 0.2876453863487072 0.359918722306265 0.4323377295457771 0.5049028489254237 0.5776145230841614 0.6504731964507151 0.723479315252554 0.7966333275250914 0.8699356831207989 0.9433868337184332 1.0169872328323528 1.0907373358217747 1.1646375999002494 1.2386884841450758 1.3128904495067601 1.3872439588186403 1.4617494768065278 ・放射強制力の増加量は最悪想定に対して倍増するが、alpha0の定量的な寄与度に依存する 放射強制力の年率増加割合=4%で徐々に変化した場合、20年間1年毎の温度変化を示す ※放射強制力のtotal増加割合=80%(非現実的な仮想実験) ・実行文 heat0d_evolution[1](s_1day*30*365*year,s_1day*30,0,1-0.04*year,1,1)=> ※本来、式変数内部のalpha1に変化量を反映するが、式変数のargumentsのkalpha1に反映 ・20年間1年毎の温度変化量dT[℃] 0 2.979166666666657 6.217391304347817 9.750000000000004 13.619047619047603 17.87499999999998 22.578947368421034 27.805555555555557 33.647058823529385 40.21874999999996 47.666666666666636 56.17857142857139 65.99999999999991 77.45833333333327 90.99999999999997 107.24999999999994 127.111111111111 151.9375 183.85714285714275 226.41666666666623 285.99999999999943 albedoの低下割合=5%が即座に反映された場合、年間30日毎の温度変化を示す ※albedoのtotal低下割合=5% ・実行文 heat0d_evolution[1](s_1day*30,s_1day,0,1,0.95,1)=> ・年間30日毎の温度変化量dT[℃] 0 0.6928618593593683+O(4e-13) 1.0723994396432488+O(2e-13) 1.2803034726072653+O(1e-13) 1.3941896571858017+O(7e-14) 1.4565745126065757+O(4e-14) 1.4907478427631133+O(2e-14) 1.5094673939444228+O(1e-14) 1.5197216359168664+O(1e-14) 1.5253387299065366+O(7e-15) 1.5284156755231315+O(4e-15) 1.530101172391248 1.5310244580278578 albedoの年率低下割合=0.25%で徐々に変化した場合、20年間1年毎の温度変化を示す ※albedoのtotal低下割合=5% ・実行文 heat0d_evolution[1](s_1day*30*365*year,s_1day*30,0,1,1-0.0025*year,1)=> ※本来、式変数内部のalbedoに変化量を反映するが、式変数のargumentsのkalbedoに反映 ・20年間1年毎の温度変化量dT[℃] 0 0.07660714285713155 0.1532142857142773 0.22982142857142307 0.3064285714285706 0.38303571428570216 0.4596428571428479 0.5362499999999901 0.6128571428571234 0.6894642857142692 0.7660714285714203 0.8426785714285607 0.9192857142857171 0.9958928571428505 1.0724999999999874 1.149107142857126 1.2257142857142718 1.302321428571414 1.3789285714285633 1.455535714285709 1.5321428571428548 放射強制力||代表温度とalbedoの各変化量に有意な相関を想定する一例を以下に示す 放射強制力の年率増加割合=0.1%、 albedoの年率低下割合=0.25%で徐々に変化した場合、20年間1年毎の温度変化を示す ※放射強制力のtotal増加割合=2% ※albedoのtotal低下割合=5% ・実行文 heat0d_evolution[1](s_1day*30*365*year,s_1day*30,0,1-0.001*year,1-0.0025*year,1)=> ※本来、式変数内部に相関を反映するが、式変数のargumentsに反映 ・20年間1年毎の温度変化量dT[℃] 0 0.1482553982553938 0.29680790151732417 0.445658403782776 0.5948078026391475 0.7442569992821273 0.8940068985340623 1.0440584088620426 1.194412442396306 1.34506991494883 1.496031746031747 1.6472988588762156 1.798872180451145 1.9507526414821221 2.1029411764706047 2.255438723712821 2.408246225319406 2.5613646272344255 2.7147948792551766 2.868537935051709 3.022594752186585 放射強制力の年率増加割合=0.05%、 albedoの年率低下割合=0.125%で徐々に変化した場合、20年間1年毎の温度変化を示す ※放射強制力のtotal増加割合=1% ※albedoのtotal低下割合=2.5% ・実行文 heat0d_evolution[1](s_1day*30*365*year,s_1day*30,0,1-0.0005*year,1-0.00125*year,1)=> ※本来、式変数内部に相関を反映するが、式変数のargumentsに反映 ・20年間1年毎の温度変化量dT[℃] 0 0.0740906167369264 0.1482553982553938 0.22249445596967554 0.29680790151732417 0.37119584675976114 0.445658403782776 0.5201956848971445 0.5948078026391475 0.6694948697711229 0.7442569992821273 0.8190943043884058 0.8940068985340623 0.9689948953914733 1.0440584088620426 1.1191975530766385 1.194412442396306 1.2697031914127201 1.34506991494883 1.4205127280594212 1.496031746031747 ※有効桁数4桁程度 |
|
目次
時間発展 の解法 |
時間発展(時間積分)の解法について記述する
時間発展の解法を列挙する ・線形system論 ・陰||陽解法 |
|
目次
線形 system論 |
線形system論について記述する
線形systemの制御理論(平衡状態に対する外乱の応答を線形近似で記述) ・状態方程式:1階線形定数係数常微分方程式の連立線形微分方程式 |
|
目次
陰||陽解法 |
陰||陽解法について記述する
1次遅れ系の時間発展方程式 ・1階線形常微分方程式 V'=-a*V+b*I ・時定数:1/a ・係数:b ・独立変数:I ・従属変数:V 時間微分:V' 右辺の関数 ・陽解法:既知(oldを付与) ・陰解法:未知(newを付与) 1次精度の有限差分 ・陽解法:Euler前進差分(explicit Euler method) ・陰解法:Euler後退差分(implicit Euler method) ・離散化誤差:Order(dt) 漸化式の導出 ・時間刻み:dt ・Euler前進差分:(newV-oldV)/dt=-a*oldV+b*I ⇒ newV=(1-a*dt)*oldV+b*dt*I ・Euler後退差分:(newV-oldV)/dt=-a*newV+b*I ⇒ newV=(oldV+b*dt*I)/(1+a*dt) ・時定数:Tc=1/a 漸化式の数値的安定性の要件(安定条件) ・前提:a>0 ・Euler前進差分:|1-a*dt|≤1 ⇒ 0≤dt≤2/a(0≦時間刻み≦時定数*2) Ver.2.51.25以降、Von Neumannの安定性解析結果から時定数の係数倍*2を追記して訂正 ・Euler後退差分:|1/(1+a*dt)|≤1 ⇒ dt≤-2/a || 0≤dt(0≦時間刻みの範囲で無条件安定) 留意事項を列挙する ・制御実装の場合、安定条件を検討する |
|
目次
常微分方程式 |
常微分方程式を列挙する
・斜方投射 ・spin ・logistic方程式 ・Lorenz方程式 ・公転軌道 |
|
目次
斜方投射 |
球の空気抵抗係数kCdA_sphereを考慮する2次元の斜方投射を一例に示す
・Ver.2.104.33以降、風速を追加考慮 ・Ver.2.655.98以降、仮定を整理 仮定を列挙する ・変形なしの剛体球 ・層流の空気抵抗を考慮 層流:抗力∝速度 乱流:抗力∝速度**2 ・進行方向に対する物体の姿勢は不変 ・進行方向に対して垂直方向の揚力は未考慮 ・浮力は未考慮 vector演算を直交座標表示の複素数演算で代替する ・t=0の複素数zの初期値 位置:z_x0=0 速度:z_v0=20+20i 加速度:z_a=0-9.8i 風速:z_u=0 ・時間刻みdtの微小区間を積分する式変数stepを定義 ・時間tの区間を積分する式変数evolutionを定義 ・step毎に位置z_xと速度z_vの連立方程式fの近似解を反復法で求解 ・陽解法 f=<{(z_x-z_x0)/dt=z_v0,m*((z_v-z_v0)/dt)=m*z_a+kCdA_sphere*(z_u-z_v0)}; ・陰解法 f=<{(z_x-z_x0)/dt=z_v,m*((z_v-z_v0)/dt)=m*z_a+kCdA_sphere*(z_u-z_v)}; ・速度の時間微分が0(抗力と重力が平衡)となる終端速度terminal velocity 0=m*z_a+kCdA_sphere*(z_u-z_v_terminal) z_v_terminal=z_u+(m/kCdA_sphere)*z_a ・抗力の大きさ=|抵抗成分の合力| Fd=kCdA_sphere*abs(z_u-z_v0)=kCdA_sphere*sqrt(real(z_u-z_v0)**2+imag(z_u-z_v0)**2) 斜方投射の解析解を示す(風速なし) clear; g=-9.8; z_a=0+g*i; z_v0=20+20i; z_x0=0; m=1; kCdA_sphere=1; k=kCdA_sphere; vt(v,a,t)=<(v-m*a/k)*exp(-k*t/m)+m*a/k; xt(x,v,a,t)=<x+((v-m*a/k)*(1-exp(-k*t/m))+a*t)*m/k; z_v(t)=<vt(real(z_v0),real(z_a),t)+vt(imag(z_v0),imag(z_a),t)i; z_x(t)=<xt(real(z_x0),real(z_v0),real(z_a),t)+xt(imag(z_x0),imag(z_v0),imag(z_a),t)i; ・時刻tの位置z_x(t) z_x(0) -> 0 z_x(1) -> 12.642411176571153+9.037192653091019i z_x(2) -> 17.293294335267746+6.16700855954894i z_x(3) -> 19.00425863264272-1.083654637362347i z_x(4) -> 19.633687222225316-9.945806038884282i z_x(5) -> 19.865241060018292-19.400790820572748i z_x(6) -> 19.950424956466673-29.07386681486466i z_x(7) -> 19.98176236068891-38.827174082573535i z_x(8) -> 19.99329074744195-48.6099967863115i z_x(9) -> 19.997531803918267-58.403677612161786i z_x(10) -> 19.99909200140475-68.20135291790692i ・時刻tの速度z_v(t) z_v(0) -> 20+20i z_v(1) -> 7.357588823428847+1.1628073469089806i z_v(2) -> 2.706705664732254-5.767008559548942i z_v(3) -> 0.9957413673572789-8.316345362637655i z_v(4) -> 0.3663127777746836-9.254193961115723i z_v(5) -> 0.13475893998170935-9.599209179427254i z_v(6) -> 0.04957504353332717-9.726133185135343i z_v(7) -> 0.018237639311090324-9.772825917426475i z_v(8) -> 0.006709252558050237-9.790003213688506i z_v(9) -> 0.002468196081733591-9.796322387838218i z_v(10) -> 0.0009079985952496969-9.798647082093078i implicit Euler methodによる1次精度の数値誤差O(dt)を含む近似解を示す clear; g=-9.8; z_a=0+g*i; z_v0=20+20i; z_x0=0; z_u=0; dt=0.5; m=1; kCdA_sphere=1; x=<{z_x,z_v}; x_initial=<{z_x0,z_v0}; f=<{(z_x-z_x0)/dt=z_v,m*((z_v-z_v0)/dt)=m*z_a+kCdA_sphere*(z_u-z_v)}; run=<last(mdx=Newton(=<f,=<x,=<x_initial),max(normc(f),normc(mdx))); /*step=<last{_rn(=<run,,3),z_x0=z_x,z_v0=z_v};*/ step=<last{_rn(=<run,,3),{$z_x0,$z_v0}=x}; evolution=<_rn(=<step,N=round(t/dt),N); ・t=0の位置z_x0, 速度z_v0 t=0; evolution; z_x0 -> 0 z_v0 -> 20+20i ・t=1の位置z_x0, 速度z_v0 t=1; evolution; z_x0 -> infoLost[ri] 11.111111111111112+6.7555555555555555i z_v0 -> infoLost[r ] 8.88888888888889+3.444444444444444i ・t=1の位置の真値(斜方投射の解析解) z_x(1) -> 12.642411176571153+9.037192653091019i z_v(1) -> 7.357588823428847+1.1628073469089806i ・t=2の位置z_x0, 速度z_v0 t=1; evolution; z_x0 -> infoLost[ri] 16.049382716049386+4.31358024691358i z_v0 -> infoLost[ri] 3.9506172839506175-3.9135802469135803i ・t=3の位置z_x0, 速度z_v0 t=1; evolution; z_x0 -> infoLost[ri] 18.244170096021953-2.216186556927298i z_v0 -> infoLost[ri] 1.755829903978052-7.183813443072703i ・t=4の位置z_x0, 速度z_v0 t=1; evolution; z_x0 -> infoLost[ri] 19.21963115378754-10.562749580856577i z_v0 -> infoLost[ri] 0.7803688462124675-8.637250419143424i ・t=5の位置z_x0, 速度z_v0 t=1; evolution; z_x0 -> infoLost[ri] 19.653169401683353-19.716777591491812i z_v0 -> infoLost[ri] 0.3468305983166522-9.28322240850819i ・t=6の位置z_x0, 速度z_v0 t=1; evolution; z_x0 -> infoLost[ri] 19.845853067414826-29.22967892955192i z_v0 -> infoLost[ri] 0.15414693258517875-9.570321070448085i ・t=7の位置z_x0, 速度z_v0 t=1; evolution; z_x0 -> infoLost[ri] 19.931490252184368-38.902079524245295i z_v0 -> infoLost[ri] 0.068509747815635-9.697920475754705i ・t=10の位置z_x0, 速度z_v0 t=3; evolution; z_x0 -> infoLost[ri] 19.99398542680357-68.20896171406268i z_v0 -> infoLost[ri] 0.006014573196434349-9.791038285937313i ・terminal velocityに収束 z_v_terminal=z_u+(m/kCdA_sphere)*z_a; z_v_terminal -> -9.8i 近似解の収束判定条件を設定する場合、stepの一例を示す ・上記の線形方程式の場合、反復3回で十分収束するため、固定値を設定 orderT=1; Nmax=10; epsf=max(eps*1e3,pow(dt,orderT)); step_pre=<{normf=max_value}; step_iteration=<_rn(=<{switch(normf>epsf,=<{normf=run})},,Nmax); step_post=<{$z_x0,$z_v0}=x; step=<last{step_pre,step_iteration,step_post}; ・t=10 t=10; evolution; x -> ( 19.993985426803565-68.20896171406268i: 0.006014573196434349-9.791038285937313i ) ・t=20 t=10; evolution; x -> ( infoLost[ i] 19.99999819124547-166.20000269504428i: infoLost[ i] 0.0000018087545367633257-9.79999730495574i ) Ver.2.29.15以降、Newton高階行列関数で収束判定条件を設定する場合 clear; g=-9.8; z_a=0+g*i; z_v0=20+20i; z_x0=0; z_u=0; dt=0.5; m=1; kCdA_sphere=1; x=<{z_x,z_v}; x_initial=<{z_x0,z_v0}; f=<{(z_x-z_x0)/dt=z_v,m*((z_v-z_v0)/dt)=m*z_a+kCdA_sphere*(z_u-z_v)}; orderT=1; Nmax=10; epsN=max(eps*1e3,pow(dt,orderT)); step_post=<{$z_x0,$z_v0}=x; step=<last{step_iteration,step_post}; evolution=<_rn(=<step,N=round(t/dt),N); ・絶対誤差指定の場合 step_iteration=<mdx=Newton(=<f,=<x,=<x_initial,,Nmax,epsN); ・t=10 t=10; evolution; x -> ( 19.993985426803565-68.20896171406268i+O(1e+1+1e+1i): 0.006014573196434349-9.791038285937313i+O(5e+0+6e+0i) ) ・t=20 t=10; evolution; x -> ( infoLost[ i] 19.99999819124547-166.20000269504428i+O(1e+1+1e+1i): infoLost[ i] 0.0000018087545367633257-9.79999730495574i+O(5e+0+6e+0i) ) ・相対誤差指定の場合 {$z_x,$z_v}=x_initial; step_iteration=<mdx=Newton(=<f,=<x,=<x_initial,,Nmax,epsN*normc(x)); ・t=10 t=10; evolution; x -> ( 19.99398542072955-68.2089617113703i+O(9e+0+8e+0i): 0.006014573196568362-9.791038285939853i+O(4e+0+7e+0i) ) ・t=20 t=10; evolution; x -> ( 19.999998167764087-166.20000267865885i+O(9e+0+8e+0i): 0.000001808754536971318-9.799997304955744i+O(4e+0+7e+0i) ) ・第7引数で相対誤差指定の場合 step_iteration=<mdx=Newton(=<f,=<x,=<x_initial,,Nmax,epsN,1); ・t=10 t=10; evolution; x -> ( 19.993985420600577-68.20896171053013i+O(1e+1+1e+1i): 0.006014573196594959-9.79103828593924i+O(5e+0+6e+0i) ) ・t=20 t=10; evolution; x -> ( 19.999998167635148-166.20000267781805i+O(1e+1+1e+1i): 0.0000018087545369793175-9.799997304955744i+O(5e+0+6e+0i) ) Ver.2.29.15以降、行列要素pattern matchingのnestingに対応 ・次のstepを許容するが、別々に記述した方が間違いが少ない clear; step=<last{mdx=Newton(=<f,=<x,=<x_initial,,Nmax,epsN),{$z_x0,$z_v0}=x}; g=-9.8; z_a=0+g*i; z_v0=20+20i; z_x0=0; z_u=0; dt=0.5; m=1; kCdA_sphere=1; x=<{z_x,z_v}; x_initial=<{z_x0,z_v0}; f=<{(z_x-z_x0)/dt=z_v,m*((z_v-z_v0)/dt)=m*z_a+kCdA_sphere*(z_u-z_v)}; orderT=1; Nmax=10; epsN=max(eps*1e3,pow(dt,orderT)); evolution=<_rn(=<step,N=round(t/dt),N); ・t=10 t=10; evolution; x -> ( 19.993985426803565-68.20896171406268i+O(1e+1+1e+1i): 0.006014573196434349-9.791038285937313i+O(5e+0+6e+0i) ) ・t=20 t=10; evolution; x -> ( infoLost[ i] 19.99999819124547-166.20000269504428i+O(1e+1+1e+1i): infoLost[ i] 0.0000018087545367633257-9.79999730495574i+O(5e+0+6e+0i) ) ODE高階行列関数を使用する場合、stepを陽的に解くため、収束演算不要 ・実軸の時間積分の場合、目安の解析誤差は実数のみ表示される(仕様) clear; g=-9.8; z_a=0+g*i; z_v0=20+20i; z_x0=0; z_u=0; dt=0.5; m=1; kCdA_sphere=1; x=<{z_x,z_v}; x_initial=<{z_x0,z_v0}; f=<{z_v,z_a+(kCdA_sphere/m)*(z_u-z_v)}; step=<{x_next=_otdummy(=<f,=<x,=<x_initial,0,dt)}; evolution=<_rn(=<step,N=round(t/dt),N); {$z_x,$z_v}=x_initial; ・t=0 t=0; evolution; x -> ( 0: 20+20i ) ・t=1 t=1; evolution; x -> ( 12.636583116319443+9.028508843315972i+O(6e-2): 7.363416883680557+1.171491156684028i+O(6e-2) ) ・t=1の位置の真値(斜方投射の解析解) z_x(1) -> 12.642411176571153+9.037192653091019i z_v(1) -> 7.357588823428847+1.1628073469089806i ・t=2 t=1; evolution; x -> ( 17.289004589856408+6.160616838886046i+O(6e-2): 2.710995410143594-5.760616838886047i+O(6e-2) ) ・t=3 t=1; evolution; x -> ( 19.001890531268412-1.0871831084100707i+O(6e-2): 0.9981094687315916-8.312816891589929i+O(6e-2) ) ・t=4 t=1; evolution; x -> ( 19.63252519430902-9.947537460479563i+O(6e-2): 0.36747480569098157-9.252462539520439i+O(6e-2) ) ・t=5 t=1; evolution; x -> ( 19.86470649057239-19.40158732904714i+O(6e-2): 0.1352935094276103-9.598412670952861i+O(6e-2) ) ・t=6 t=1; evolution; x -> ( 19.950188874421418-29.074218577112084i+O(6e-2): 0.049811125578583-9.725781422887913i+O(6e-2) ) ・t=7 t=1; evolution; x -> ( 19.981660995845978-38.827325116189485i+O(6e-2): 0.018339004154023522-9.772674883810506i+O(6e-2) ) ・t=10 t=3; evolution; x -> ( 19.999084783315336-68.20136367286014i+O(6e-2): 0.0009152166846619435-9.798636327139855i+O(6e-2) ) ・2次精度選択の場合(参考) ・t=10 t=10; evolution; x -> ( 19.998345638774897-68.20246499822541i+O(3e-1): 0.0016543612251060553-9.797535001774593i+O(3e-1) ) Ver.2.29.15以降、ODE高階行列関数第6引数で反復回数を指定する場合 clear; g=-9.8; z_a=0+g*i; z_v0=20+20i; z_x0=0; z_u=0; dt=0.5; m=1; kCdA_sphere=1; x=<{z_x,z_v}; x_initial=<{z_x0,z_v0}; f=<{z_v,z_a+(kCdA_sphere/m)*(z_u-z_v)}; stepN=<last{N=round(t/dt),x_next=_otdummy(=<f,=<x,=<x_initial,0,dt,N)}; evolution=<stepN; ・t=0 t=0; evolution; x -> ( 0: 20+20i ) ・t=5 t=5; evolution; x -> ( 19.86470649057239-19.40158732904714i+O(6e-2): 0.1352935094276103-9.598412670952861i+O(6e-2) ) ・t=10 t=5; evolution; x -> ( 19.999084783315336-68.20136367286014i+O(6e-2): 0.0009152166846619435-9.798636327139855i+O(6e-2) ) 球体周りが真空の場合、空気抵抗なし ・空気抵抗小で風速の影響を受けにくい clear; g=-9.8; z_a=0+g*i; z_v0=20+20i; z_x0=0; z_u=0; dt=0.5; m=1; kCdA_sphere=0; x=<{z_x,z_v}; x_initial=<{z_x0,z_v0}; /*f=<{z_v,z_a+(kCdA_sphere/m)*(z_u-z_v)};*/ f=<{z_v,z_a}; stepN=<last{N=round(t/dt),x_next=_otdummy(=<f,=<x,=<x_initial,0,dt,N)}; evolution=<stepN; ・t=0 t=0; evolution; x -> ( 0: 20+20i ) ・t=1 t=1; evolution; x -> ( 19.999999999999996+15.1i+O(6e-2): 20+10.2i+O(6e-2) ) ・t=2 t=1; evolution; x -> ( 39.99999999999999+20.4i+O(6e-2): 20+0.3999999999999986i+O(6e-2) ) ・解析解 clear; g=-9.8; z_x(t)=<(comp(20*t,20*t+g*t^2/2)); z_v(t)=<(comp(20,20+g*t)); t=1; (z_x(t):z_v(t)) -> (20+15.1i:20+10.2i) t=2; (z_x(t):z_v(t)) -> (40+20.4i:20+0.3999999999999986i) |
|
目次
spin |
無風状態でspin運動を追加考慮する場合、野球の解釈を参照 |
|
目次
logistic 方程式 |
古典的なlogistic方程式について記述する
解法を列挙する ・1次精度のimplicit Euler method delVar(N); N0=1; dt=1e-2; r=2; K(t)=<1e4; c(t)=<t*0; Nd(N,tdummy)=<r*N*(1-N/K(tdummy)=>)-c(tdummy)=>*N; f=<(N-oldN)/dt=Nd(N,t0)=>; evolution=<_rn(=<last{mdx=Newton(=<f,=<{N},=<{oldN},,3),t0=t0+dt,oldN=N},Nt=round(t/dt),Nt); switch(~~hasVar(t0),=<t0=0); switch(~~hasVar(oldN),=<oldN=N0); t=0.5; evolution=>; N_o1=N; Nd_o1=Nd(N_o1,t0)=>; ・4次精度のODE高階行列関数 delVar(N); N0=1; dt=1e-2; r=2; K(t)=<1e4; c(t)=<t*0; Nd(N,tdummy)=<r*N*(1-N/K(tdummy)=>)-c(tdummy)=>*N; switch(~~hasVar(t0),=<t0=0); t=0.5; N_o4=_otdummy(=<Nd,=<{N},=<{N0},Nt=round(t/dt),dt,Nt); t0=t0+Nt*dt; Nd_o4=Nd(N_o4,t0)=>; test caseを示す ・index t,N_o1,N_o4,Nd_o1,Nd_o4, ・Nが対象の総数、Ndが総数の時間変化率を表す 0,1,1,1.9998,1.9998, 0.5,2.7454835660788866,2.7178148277154164,5.489459596155451,5.434152351943283, 1,7.535337152455474,7.384338184505727,15.059318043710713,14.757770678926823, 1.5,20.66408939370309,20.047275542822188,41.24277786931199,40.01417243430641, 2,56.534907309312615,54.30707388083179,112.43057546973071,108.02429610696396, 2.5,153.69558207368877,146.25713551868418,302.66669775758356,288.23604109934223, 3,410.80167027777674,387.8217275470406,787.8517380949512,745.562316622567, 3.5,1051.229018701946,988.3466173639846,1881.4415474516807,1781.3274275170031, 4,2432.69608201103,2296.58521933111,3681.7901185356964,3538.3097047321953, 4.5,4670.8986413623725,4476.326547927924,4978.338459148573,4945.153223118983, 5,7039.913937363045,6877.797147717635,4167.7502256304,4294.775574404702, 5.5,8653.627085889626,8568.978030895896,2330.2018234507364,2452.4791629964902, 6,9454.442955734134,9421.199383322248,1031.587590822111,1090.5992025821959, 6.5,9790.254671395429,9778.984831271717,410.6920366348549,432.26079649496876, 7,9921.053211573017,9917.541043635658,156.6470577733799,163.55801683174664, 7.5,9970.525679870507,9969.506098757523,58.774893149567546,60.801826882355876, 8,9989.02954450271,9988.76025510466,21.91684081581646,22.454223417616358, 8.5,9995.921412967771,9995.862189060947,8.153847090022257,8.272197582235348, 9,9998.48431030025,9998.47738616784,3.0309199364497452,3.04476399374143, 9.5,9999.436826421514,9999.439807756415,1.1262837240763395,1.1203217240999352, 10,9999.790758052437,9999.793909492353,0.4184751386874744,0.4121725206351419, |
|
目次
Lorenz 方程式 |
chaosを記述するLorenz方程式について記述する
解法を列挙する ・1次精度のimplicit Euler method x0=1; y0=1; z0=1; dt=1e-2; sigma=10; rho=28; beta=8/3; oldX={x0,y0,z0}; x=<{x,y,z}; f=<{(x=>-oldX)/dt={sigma*(y-x),x*(rho-z)-y,x*y-beta*z}}; evolution=<_rn(=<last{mdx=Newton(=<f,=<x,=<{oldX},,3),oldX=x=>},N=round(t/dt),N); t=0.5; evolution=>; x_o1=x=>; ・4次精度のODE高階行列関数 x0=1; y0=1; z0=1; dt=1e-2; sigma=10; rho=28; beta=8/3; t=0.5; x1=_otdummy(=<{sigma*(y-x),x*(rho-z)-y,x*y-beta*z},=<{x,y,z},=<{x0,y0,z0},N=round(t/dt),dt,N); x_o4=x1; test caseを示す ・index t,x_o1[0],x_o1[1],x_o4[0],x_o4[1], ・dt=1e-2の場合、精度不足で非線形性を再現できない(局所解に収束する)問題が生じる 0,1,1,1,1, 0.5,3.17226169537662,-4.256695788682715,1.1985649578564037,-8.867139000908747, 1,-12.593886034890854,-12.566332541538133,-9.378615807236292,-8.357059955292334, 1.5,-7.969019258310487,-11.31490088661472,-9.672344085493663,-10.43202539469619, 2,-5.494882221001438,-6.150075249562857,-8.17344249034626,-9.561995763765363, 2.5,-6.918422768097526,-5.051034065354747,-6.9595105515652,-7.272367096863916, 3,-9.799081256658823,-8.120947564464892,-7.456678927032095,-6.190930885532192, 3.5,-9.877085779613125,-10.874997665172218,-9.440140717611673,-7.908072783200122, 4,-8.139992152005245,-9.432369431846958,-10.090694528965873,-10.930593746741103, 4.5,-7.3870744310535414,-7.570822540188955,-8.160304033711654,-9.95637917564153, 5,-7.984501338275579,-7.235749139770024,-6.512011104065696,-6.973829714945723, 5.5,-8.920492826915343,-8.318139793906798,-7.062966879708615,-5.494413072210336, 6,-9.038027186303783,-9.248356246040178,-9.74236661556773,-7.707169464228651, 6.5,-8.49305006616133,-8.976234963391228,-10.464396660745086,-11.832478447991546, 7,-8.130804720845779,-8.28239729731554,-7.664176375307848,-9.841271349824467, 7.5,-8.259705679353072,-8.039739814958851,-5.764002076296161,-6.010244144594397, 8,-8.58280219213773,-8.344656625443,-7.012807499828442,-4.58586813222329, 8.5,-8.688994731402035,-8.700446853708815,-10.897712384454998,-8.936331299714656, 9,-8.53705846661493,-8.69771111037465,-9.98129478780655,-12.930613559534246, 9.5,-8.38266878209243,-8.468750160768215,-5.875523774590598,-7.717394289287349, 10,-8.389870588016631,-8.337134834882676,-4.902819483748834,-3.743407675271704, ・4次精度の場合、2個の局所解の周辺軌道を不規則に周回する 10.5,-8.495685199019016,-8.407065481138382,-9.369506554182164,-5.010958534812629, 11,-8.553889675164031,-8.536838303263686,-11.662532595710633,-14.81547566296874, 11.5,-8.518326078119987,-8.566390748672115,-5.159309948252431,-7.585562008100757, 12,-8.459785890514121,-8.49893468356178,-3.343568426347868,-1.981261293883908, 12.5,-8.448581390548986,-8.44040444050926,-11.898976041789902,-6.3712542924118445, 13,-8.480263581411933,-8.449722477379298,-5.733524002666311,-9.826784960075946, 13.5,-8.506362651808852,-8.493758526098969,-0.3802259177270047,0.6660876610219357, 14,-8.500914879165052,-8.51353704745702,8.74913755997124,16.24710906182236, 14.5,-8.480664452700042,-8.496293816310711,-4.275750718936878,-6.475025393880294, 15,-8.472332385769134,-8.473289725359022,-4.385295763938703,-2.064285615514298, 15.5,-8.480669993019669,-8.47100068916237,-12.621236499143057,-9.01894997684598, 16,-8.491044281197345,-8.484724178151444,-6.579354658092149,-10.806497343325686, 16.5,-8.491685120893191,-8.494304255831391,-1.3541368707518615,-0.861479586035053, 17,-8.485273037728508,-8.490945179480132,-15.37505265390411,-12.037916661021102, 17.5,-8.481085762467366,-8.482709343044847,4.446642477408391,7.609243521330697, 18,-8.48281709988944,-8.480060745027655,0.8353916008229954,-0.8464235152808502, 18.5,-8.486577544441795,-8.48389235255966,-6.809029480225468,-12.918873053525699, 19,-8.487656376907653,-8.487881913737274,3.592870892275928,5.582259866891, 19.5,-8.485829504763153,-8.487719232205539,5.189810855800015,1.8557333971653025, 20,-8.48404945484628,-8.485013299511959,13.472905743504375,12.691475056130807, 20.5,-8.48419785398612,-8.48352824576874,5.008483778052009,8.211340043414769, 21,-8.485450226986057,-8.484425380266224,1.5015702673757763,0.20812959396276343, 21.5,-8.48608982998104,-8.485925342322853,14.401370086245281,20.658564549794743, 22,-8.485646326915106,-8.486220315736853,-3.806256312326124,-6.211498088214414, 22.5,-8.484966923511978,-8.485412158330154,-2.3354311831168686,0.07190386522249949, 23,-8.484857552599165,-8.484743812358335,-12.209487160940686,-19.601380033191635, 23.5,-8.48523786836849,-8.4848795569143,2.7993938471698048,4.574587624158835, 24,-8.485533165665105,-8.485396850853348,3.4482351977325516,-0.6854593741996927, 24.5,-8.485457942939185,-8.485612274035551,5.02452981820134,9.465219719283413, 25,-8.485220438665973,-8.485400423783547,-2.3073578344925263,-4.189639088627373, 25.5,-8.485129972575944,-8.485134837038022,-7.247375872344094,-1.7600541085053956, 26,-8.485232199001693,-8.485117264300568,-11.732669460801114,-17.16226971887629, 26.5,-8.485351537934092,-8.485280749590473,-1.433846374145607,-2.050391844767691, 27,-8.485354827395978,-8.485388412748176,-7.792998035684965,1.243449129681648, 27.5,-8.48527865837135,-8.485344741437403,9.030593020023082,14.998609771176515, 28,-8.485231703764377,-8.485248593015273,0.009487723492419137,-0.4280251283303371, 28.5,-8.485253935528434,-8.485220620258763,-10.922695871555433,-19.685895742160522, 29,-8.48529774285777,-8.485267093274015,5.418273580329954,8.019543065901978, 29.5,-8.485308960017305,-8.485312736156105,4.155173942366574,3.0328376377692177, 30,-8.48528688716803,-8.485309167527985,9.866856999805194,4.649624477361923, 30.5,-8.485266562792274,-8.485277196596934,10.599275723617525,15.513123005714233, 31,-8.485269054140165,-8.485260727038607,2.819872641839744,3.972613974971094, 31.5,-8.485283821293933,-8.485271963782196,4.419437977786595,-0.4438293434975797, 32,-8.485290876746973,-8.485289352091629,6.630942216231427,12.111942524616314, 32.5,-8.485285362023996,-8.485292225643086,-2.0057820792846255,-3.5378845440162534, 33,-8.485277500703758,-8.48528253568819,-7.046099221729282,-0.6580015299230573, 33.5,-8.485276485949097,-8.485274955455953,-7.203466930850314,-12.692315663749156, 34,-8.485281034092166,-8.48527683860395,0.995678432365439,2.0958489939235863, 34.5,-8.485284373416704,-8.485282907318853,11.215000312655096,2.7343773034648136, 35,-8.48528336095452,-8.485285244435245,-3.739160222899354,-6.731326586869997, 35.5,-8.485280579934958,-8.485282647307939,0.3065513361083291,2.5422078966809663, 36,-8.48527960678275,-8.485279590114972,13.58829662387021,8.764145152786396, 36.5,-8.485280854479951,-8.485279491637526,0.9639221116027187,1.6891302902255667, 37,-8.485282225270273,-8.485281434562172,6.803463917158995,-3.6259293367169434, 37.5,-8.485282214978417,-8.485282641830935,-12.635586600601137,-14.94102981764714, 38,-8.485281311780499,-8.48528208034935,-5.028693841288827,-7.762652378103106, 38.5,-8.485280787260102,-8.485280959965065,-2.5959502775517938,-1.2565930246417043, 39,-8.485281069858013,-8.485280668435113,-13.855447688722043,-9.595402777994904, 39.5,-8.485281579364718,-8.48528123021927,-0.8552233742457771,-1.4872041441677788, 40,-8.485281694101317,-8.485281751456034,-8.204088513176726,2.971896470484188, 40.5,-8.485281428130728,-8.485281690372483,12.30113519381589,15.112064169246912, 41,-8.485281196596342,-8.485281313308466,4.941766939450534,7.512328766658172, 41.5,-8.48528123447943,-8.485281131498912,2.830640134963891,1.3757448822441196, 42,-8.485281408294911,-8.485281271337463,13.540754286837664,9.112933983634957, 42.5,-8.485281485738815,-8.485281472579084,1.9255517778563045,3.376910384682569, 43,-8.485281417533477,-8.485281499427858,2.027623330485493,-3.426815186275571, 43.5,-8.485281326730567,-8.48528138351308,-13.994404485457153,-14.457830777576898, 44,-8.485281317959297,-8.485281297760862,-2.997574418412171,-4.985503100124961, 44.5,-8.485281372228071,-8.485281323184875,-1.734332465373308,1.648909612702126, 45,-8.485281409889234,-8.485281394261605,10.912351558935278,18.351057979919684, 45.5,-8.485281396523915,-8.485281419429246,-2.5985424770556107,-4.241652829020272, 46,-8.485281364014313,-8.485281387714952,-4.125932852203712,0.5787713043516732, 46.5,-8.485281353639579,-8.48528135258926,-5.657770524690035,-10.510383035401476, 47,-8.48528136881385,-8.485281352684646,2.120269736613679,3.8274800845271506, 47.5,-8.48528138452925,-8.485281375729544,7.266636590609533,1.2741164340714035, 48,-8.485281383841825,-8.485281389222006,9.892365266534018,16.067979563412507, 48.5,-8.485281373152189,-8.485281382075945,0.04917319797390527,-0.2788585959341874, 49,-8.485281367314501,-8.48528136904223,-7.113774784122735,-13.877250849565106, 49.5,-8.485281370876883,-8.48528136605278,4.915037380671982,7.144347716592804, 50,-8.485281376792848,-8.485281372824582,5.220407960904293,3.407556829118244, 50.5,-8.485281377941114,-8.48528137876424,10.52690922410113,6.5181811522742175, 51,-8.485281374744686,-8.485281377825963,10.65055098668909,14.636296491495415, 51.5,-8.485281372113047,-8.485281373386725,4.402541930945902,6.206654869158568, 52,-8.485281372657107,-8.485281371389663,3.8125459872364202,1.4776073716073355, 52.5,-8.485281374699461,-8.485281373120367,13.648774132656863,10.987960253004305, 53,-8.48528137554469,-8.485281375445382,3.7435020489424766,6.389538561909723, 53.5,-8.485281374705183,-8.485281375680245,0.8698171874372583,-1.4286371678428293, 54,-8.485281373658209,-8.485281374296731,-12.89165079047701,-20.22815651871761, 54.5,-8.48528137359182,-8.48528137332924,3.2321161489793213,5.251652861636881, 55,-8.485281374237987,-8.485281373665638,2.9674179947150368,-0.3362507323658391, 55.5,-8.485281374661513,-8.485281374496711,9.4413393746746,16.5411839612538, 56,-8.485281374487728,-8.48528137476538,-2.520246590198456,-4.116293588931646, 56.5,-8.485281374108316,-8.485281374379491,-4.804880501581975,0.2330160206531241, 57,-8.485281373998893,-8.48528137397668,-7.863372311800565,-13.981444909642125, 57.5,-8.48528137418284,-8.485281373992304,1.7436584968150188,3.0671010343042724, 58,-8.485281374362652,-8.485281374265119,7.229422505535066,0.03987829269415222, 58.5,-8.485281374348029,-8.48528137441536,1.5631123613527964,2.925582469651283, 59,-8.485281374221744,-8.485281374325186,1.2145147117244712,-4.835323974328813, 59.5,-8.485281374157037,-8.485281374173812,-12.12357764900539,-9.208819929792327, 60,-8.48528137420162,-8.485281374143788,-8.35535702135332,-12.78856598394072, 60.5,-8.485281374270201,-8.485281374225204,-2.8193222160385707,-3.358298556407861, 61,-8.485281374281358,-8.485281374292743,-6.409036998156865,-0.5100831005913947, 61.5,-8.485281374243032,-8.485281374279175,-8.702695081277174,-14.888753153809706, 62,-8.485281374213196,-8.485281374227002,0.8694012848614923,1.7500370844583035, 62.5,-8.485281374220731,-8.485281374205199,11.927236014273815,2.9926611975532866, 63,-8.485281374244678,-8.485281374226513,-6.433279521071849,-11.058343035346425, 63.5,-8.485281374253836,-8.485281374253312,-0.1945686430280429,0.657452773229513, 64,-8.485281374243556,-8.485281374255132,11.064697253901878,19.51445824215947, 64.5,-8.48528137423151,-8.485281374238667,-4.763770339918941,-7.247196079841023, 65,-8.485281374231148,-8.48528137422778,-3.7524336250868964,-2.090436251238726, 65.5,-8.485281374238827,-8.48528137423216,-11.972740287007628,-6.992918533876928, 66,-8.485281374243574,-8.48528137424186,-6.673978384860627,-11.151921454407349, 66.5,-8.485281374241344,-8.485281374244693,-0.8834124396847836,-0.30243385842138293, 67,-8.485281374236932,-8.485281374240024,-14.98911908041907,-21.37882101859409, 67.5,-8.48528137423579,-8.485281374235422,5.13161494004057,8.14985336407378, 68,-8.48528137423801,-8.485281374235765,2.5573143746420555,1.3794701581657898, 68.5,-8.48528137424006,-8.485281374238983,13.414225004473133,8.345175272489065, 69,-8.48528137423981,-8.485281374240644,1.1921993682630823,2.099260564479773, 69.5,-8.485281374238328,-8.485281374239522,4.827645626791041,-4.0221928043110635, 70,-8.485281374237612,-8.485281374237768,-13.101666561681263,-14.633906343724416, 70.5,-8.485281374238165,-8.485281374237474,-4.872219355915312,-7.71272847935955, 71,-8.485281374238957,-8.48528137423845,-2.1653833332340966,-0.7438238426403552, 71.5,-8.48528137423906,-8.48528137423921,-15.204024707302196,-14.63043131908489, 72,-8.485281374238612,-8.48528137423903,1.7975268141620369,3.1455696671801285, 72.5,-8.485281374238268,-8.48528137423842,3.0153550146952126,-3.1014834469110224, 73,-8.485281374238367,-8.485281374238177,-13.7282565109969,-17.116902242160016, 73.5,-8.485281374238651,-8.485281374238445,-1.489025066097232,-2.365996643630202, 74,-8.485281374238747,-8.48528137423875,-5.6331972944620805,2.5691308714425447, 74.5,-8.48528137423862,-8.485281374238756,11.796061315007085,17.493862052365486, 75,-8.485281374238482,-8.485281374238555,0.8826834247272499,1.187173843603535, 75.5,-8.485281374238493,-8.485281374238445,12.885473543264979,3.3206833869114876, 76,-8.48528137423858,-8.485281374238507,-9.124515539388067,-14.285340874716285, 76.5,-8.485281374238625,-8.485281374238616,-1.951071216638205,-2.4041477887189995, 77,-8.485281374238602,-8.48528137423864,-7.7900769938714545,0.09504956422547406, 77.5,-8.485281374238552,-8.485281374238586,2.058089752981872,3.839027119270948, 78,-8.48528137423854,-8.48528137423854,0.1914164597509504,-4.281599119512394, 78.5,-8.485281374238573,-8.485281374238546,-11.955293412139545,-7.890279902848384, 79,-8.485281374238586,-8.485281374238586,-8.010063905586513,-12.715658508594974, 79.5,-8.485281374238575,-8.485281374238584,-1.9644535716511302,-2.1302416924982674, 80,-8.485281374238575,-8.485281374238584,-9.259937328836994,-1.1479943729401354, 80.5,-8.485281374238575,-8.485281374238584,0.9224828383264055,1.716019126125542, 81,-8.485281374238575,-8.485281374238584,5.439250814741619,-4.7740078423318595, 81.5,-8.485281374238575,-8.485281374238584,-12.473249232276745,-12.716617996056636, 82,-8.485281374238575,-8.485281374238584,-7.04621429967117,-10.611460577747751, 82.5,-8.485281374238575,-8.485281374238584,-3.2455994211194317,-3.285194408231794, 83,-8.485281374238575,-8.485281374238584,-7.617993626335245,-1.7980328385564948, 83.5,-8.485281374238575,-8.485281374238584,-10.83763848272238,-16.704591991598893, 84,-8.485281374238575,-8.485281374238584,-0.9038557384560206,-1.1232976680235789, 84.5,-8.485281374238575,-8.485281374238584,-13.616876132303181,-4.907109779522588, 85,-8.485281374238575,-8.485281374238584,8.375880249689722,13.404983862615476, 85.5,-8.485281374238575,-8.485281374238584,1.6724997896490716,1.8393457405000158, 86,-8.485281374238575,-8.485281374238584,10.17661658191445,1.5413857465803245, 86.5,-8.485281374238575,-8.485281374238584,-3.7171164521760556,-6.741612648752846, 87,-8.485281374238575,-8.485281374238584,0.5109315454990305,2.765987073343893, 87.5,-8.485281374238575,-8.485281374238584,12.754453918387487,7.077823084672719, 88,-8.485281374238575,-8.485281374238584,2.379502374400508,4.219324154193406, 88.5,-8.485281374238575,-8.485281374238584,0.9726930126341234,-3.1513732544147244, 89,-8.485281374238575,-8.485281374238584,-14.101460932573618,-12.796325106546512, 89.5,-8.485281374238575,-8.485281374238584,-2.662042387422041,-4.525493684718707, 90,-8.485281374238575,-8.485281374238584,-1.5832230408193584,2.2640062717003593, 90.5,-8.485281374238575,-8.485281374238584,14.055963676220127,18.85628561568353, 91,-8.485281374238575,-8.485281374238584,-1.103227563518522,-1.93389960675635, 91.5,-8.485281374238575,-8.485281374238584,-7.739740817677188,2.0043108944443504, 92,-8.485281374238575,-8.485281374238584,11.338202783621735,16.72385353830341, 92.5,-8.485281374238575,-8.485281374238584,1.7526147189102084,2.497503922991857, 93,-8.485281374238575,-8.485281374238584,6.444142727074921,-1.4086050396384013, 93.5,-8.485281374238575,-8.485281374238584,-7.243434835338782,-12.786299691351037, 94,-8.485281374238575,-8.485281374238584,1.0642357241355014,2.1843861788415273, 94.5,-8.485281374238575,-8.485281374238584,10.747687952180504,2.235709574223687, 95,-8.485281374238575,-8.485281374238584,-3.3830321213009897,-6.131458259894062, 95.5,-8.485281374238575,-8.485281374238584,0.31691862028692325,2.8571001945419865, 96,-8.485281374238575,-8.485281374238584,13.065327355962134,8.030918760284983, 96.5,-8.485281374238575,-8.485281374238584,2.694907719649491,4.74230777743698, 97,-8.485281374238575,-8.485281374238584,0.8017555363215676,-2.7565303334961193, 97.5,-8.485281374238575,-8.485281374238584,-14.519581857486784,-13.9341653534679, 98,-8.485281374238575,-8.485281374238584,-1.109323287567829,-1.8645313362139673, 98.5,-8.485281374238575,-8.485281374238584,-6.681147405835485,3.110341873902442, 99,-8.485281374238575,-8.485281374238584,12.566399664438359,16.21728929382193, 99.5,-8.485281374238575,-8.485281374238584,3.4726030958641747,5.377321968870701, 100,-8.485281374238575,-8.485281374238584,2.690822604312346,-0.36347536026915495, 100.5,-8.485281374238575,-8.485281374238584,9.129990791825188,16.190917967986504, 101,-8.485281374238575,-8.485281374238584,-2.712051392028709,-4.38960428675254, 101.5,-8.485281374238575,-8.485281374238584,-4.707153543160363,-0.0624252945859471, 102,-8.485281374238575,-8.485281374238584,-10.519992200138974,-17.342044829062676, 102.5,-8.485281374238575,-8.485281374238584,1.2482669398645023,2.213816171403173, 103,-8.485281374238575,-8.485281374238584,8.409525938132676,-0.5744300757713541, 103.5,-8.485281374238575,-8.485281374238584,-7.411868226149255,-12.825959845831905, 104,-8.485281374238575,-8.485281374238584,0.436137494080987,1.2894320737131153, 104.5,-8.485281374238575,-8.485281374238584,15.58532196492229,11.615271399347568, 105,-8.485281374238575,-8.485281374238584,-5.915346993228955,-9.860381207389619, 105.5,-8.485281374238575,-8.485281374238584,-1.2181631139997258,-0.4263482462662149, 106,-8.485281374238575,-8.485281374238584,-15.663930860898642,-19.33937255552515, 106.5,-8.485281374238575,-8.485281374238584,4.521561593727568,7.4326480506935715, 107,-8.485281374238575,-8.485281374238584,1.85291826931102,0.2161149426988998, 107.5,-8.485281374238575,-8.485281374238584,14.42804764968092,20.17160748079123, 108,-8.485281374238575,-8.485281374238584,-3.1991918425499453,-5.298266966954755, 108.5,-8.485281374238575,-8.485281374238584,-2.370380765599638,0.8177781451543822, 109,-8.485281374238575,-8.485281374238584,-2.184555200459103,-4.245710333289834, 109.5,-8.485281374238575,-8.485281374238584,1.3408379642226849,5.1956407713584545, 110,-8.485281374238575,-8.485281374238584,9.637088360556053,5.254857248067809, 110.5,-8.485281374238575,-8.485281374238584,11.44479313901552,14.934045964834992, 111,-8.485281374238575,-8.485281374238584,4.849657160898645,7.08275548033174, 111.5,-8.485281374238575,-8.485281374238584,3.3949455366195216,1.7117047396435543, 112,-8.485281374238575,-8.485281374238584,12.798538699303482,8.147308153915688, 112.5,-8.485281374238575,-8.485281374238584,4.501204000321512,7.768890986434246, 113,-8.485281374238575,-8.485281374238584,0.4313529081167843,-1.2438125807876403, 113.5,-8.485281374238575,-8.485281374238584,-14.011328552200109,-20.82356065365446, 114,-8.485281374238575,-8.485281374238584,3.8602587804259874,6.255891828916169, 114.5,-8.485281374238575,-8.485281374238584,2.498002598696069,0.12067888046271247, 115,-8.485281374238575,-8.485281374238584,13.633821106730984,19.88958278458403, 115.5,-8.485281374238575,-8.485281374238584,-2.381792503597005,-3.9832960613508086, 116,-8.485281374238575,-8.485281374238584,-3.3164981824151503,1.5568035956093136, 116.5,-8.485281374238575,-8.485281374238584,6.097852316468226,11.295735062464985, 117,-8.485281374238575,-8.485281374238584,-2.230815916474438,-3.898774950574807, 117.5,-8.485281374238575,-8.485281374238584,-6.822869886437022,-1.0113620407830788, 118,-8.485281374238575,-8.485281374238584,-10.148965209364832,-16.426478743019562, 118.5,-8.485281374238575,-8.485281374238584,0.08618466303046382,0.46165572908901864, 119,-8.485281374238575,-8.485281374238584,13.447002495566332,22.28296738788286, 119.5,-8.485281374238575,-8.485281374238584,-6.079488391552779,-9.065677171169286, 120,-8.485281374238575,-8.485281374238584,-3.826642222965666,-3.289750553058409, 120.5,-8.485281374238575,-8.485281374238584,-8.68196802847738,-3.24658977979292, 121,-8.485281374238575,-8.485281374238584,-11.43757717336926,-16.297820532529098, 121.5,-8.485281374238575,-8.485281374238584,-2.664871949390741,-3.9104450021129296, 122,-8.485281374238575,-8.485281374238584,-4.037895097255778,0.8869858747612515, 122.5,-8.485281374238575,-8.485281374238584,-2.061900522854889,-3.947178772303834, 123,-8.485281374238575,-8.485281374238584,0.6694855167786125,4.894178580531529, 123.5,-8.485281374238575,-8.485281374238584,10.51162534190327,6.075633801086092, 124,-8.485281374238575,-8.485281374238584,10.472694199091322,14.901552160284407, 124.5,-8.485281374238575,-8.485281374238584,3.6919227591623676,5.18245713901584, 125,-8.485281374238575,-8.485281374238584,3.943653390259663,0.6372579228212448, 125.5,-8.485281374238575,-8.485281374238584,14.166577288157871,17.589193640565423, 126,-8.485281374238575,-8.485281374238584,0.27261787162322987,0.36217868776741036, 126.5,-8.485281374238575,-8.485281374238584,16.36054986477835,22.904192442279463, 127,-8.485281374238575,-8.485281374238584,-7.660340651616426,-11.09869077894772, ・dt=1.5e-2の場合 0,1,1,1,1, 0.5,4.259440073750432,-2.5422528544767817,1.716327431040365,-8.87664912115545, 1,-12.0884496431265,-17.189432027928923,-9.326501713302648,-8.251909113757243, 1.5,-4.936964411309114,-6.941998855453551,-9.672577878994444,-10.432651307781377, 2,-5.6565380639518095,-4.228040591612055,-8.104213207812785,-9.470757660369454, 2.5,-9.098885692720897,-6.697769952414515,-6.976215521684386,-7.351324317471985, 3,-10.130283760557962,-10.594052417158737,-7.456653999063002,-6.190342589063736, 3.5,-8.470564576268435,-9.71062658558134,-9.515961578414334,-8.043295860202447, 4,-7.7078809453369175,-8.101702302091462,-10.130458222070452,-10.874127376035716, 4.5,-8.022020459009896,-7.5997829691697065,-8.159431122315882,-9.955754377419897, 5,-8.679277322471625,-8.26611245440508,-6.490049196618602,-6.876143681805971, 5.5,-8.800734858681437,-8.81370204931446,-6.986659429415132,-5.490094778899708, 6,-8.54356961421768,-8.767245285410315,-9.743889752863609,-7.7089653668223495, 6.5,-8.349272580370922,-8.436775134268553,-10.39260003785368,-11.876351717495224, 7,-8.386816856578445,-8.32685433338917,-7.772192813202849,-9.996736366912055, 7.5,-8.504097887947003,-8.42307532205577,-5.762969356060709,-6.007693795407455, 8,-8.543548213304565,-8.540302848877742,-7.138142836095743,-4.626091180549186, 8.5,-8.50565558023525,-8.542532046982556,-10.79836913917521,-8.669558912625227, 9,-8.46510690111595,-8.486888158485604,-9.977814753220104,-12.929550835409694, 9.5,-8.466250910993233,-8.456769814682035,-5.782133739789961,-7.53191078205841, 10,-8.485182998714278,-8.469957964316489,-4.848193620800469,-3.804360224606302, ・dt=2e-2の場合、別の局所解に収束する 0,1,1,1,1, 0.5,4.609560287868656,-1.1598359230291724,1.2037115346927614,-8.864627279249813, 1,0.6791070531707077,1.287644827905354,-9.380072097163998,-8.35720377438337, 1.5,7.82965716020545,1.1901109306698194,-9.673597042084705,-10.43508485198912, 2,10.003531745807148,15.350382624653745,-8.171968022207809,-9.562054344092918, 2.5,5.384529232520461,6.8173925970264095,-6.957096007098234,-7.269340551950377, 3,6.690133256550868,5.432849246652645,-7.4563074119789405,-6.187943808083866, 3.5,9.076409185262547,7.715548750146841,-9.443195007212195,-7.910145722770152, 4,9.36339001689963,9.597868219982363,-10.09157879362887,-10.935720605138682, 4.5,8.523958071479683,9.1051519969965,-8.156398509948643,-9.953855904768098, 5,8.156375943911566,8.30093275236233,-6.508248278510195,-6.96758959112482, 5.5,8.329059685395057,8.162703091357479,-7.064244495700321,-5.490536575142012, 6,8.551735541731087,8.42395265134481,-9.749305554038418,-7.714931887852475, 6.5,8.573248534336193,8.589798794243883,-10.462791383678454,-11.840496844640382, 7,8.49373408277786,8.550442101496914,-7.6548110385705455,-9.83101488497078, 7.5,8.453930292941367,8.470213685143923,-5.758895020213391,-5.998280672057063, 8,8.469254466331492,8.453447318778185,-7.020684060061325,-4.58312605529452, 8.5,8.491225553407192,8.478397052477131,-10.911214722690017,-8.964188351637576, 9,8.494002020714802,8.495117187256911,-9.965206194133534,-12.92613609199428, 9.5,8.486428684029079,8.491944650943209,-5.858059307937853,-7.689346038427618, 10,8.48229483900468,8.484070027063778,-4.904942438971408,-3.7262179876698824, ・dt=1e-1の場合 0,1,1,1,1, 0.5,7.052448116495055,3.3451344690621716,0.9517378983696467,-7.3998783669487365, 1,9.208909501591917,9.462443595514857,-10.184761919410535,-8.879316933775975, 1.5,8.374194357920478,8.439139686020075,-9.837027973304629,-11.632276786730488, 2,8.489276659789128,8.46702441296707,-7.226475577082166,-8.861625926441459, 2.5,8.487677790123978,8.490745880413645,-6.229907941575721,-5.909553643903918, 3,8.484622016317676,8.484590566354681,-8.047634683014023,-5.7442419010750845, 3.5,8.48535897288969,8.485274987807683,-10.62099501442393,-9.901425701440763, 4,8.485283446082292,8.4853033255893,-9.33647110676739,-11.569977894464648, 4.5,8.485278602877734,8.485276611884489,-6.64728402698247,-7.981867945528143, 5,8.485281937908452,8.48528179681158,-6.229770298845975,-5.33401779375, 5.5,8.485281329365826,8.485281420309946,-8.81636478679008,-6.210251468023328, 6,8.485281367625436,8.485281351298857,-10.890131918033996,-11.250823695116432, 6.5,8.485281377062725,8.485281378045585,-8.472288843025853,-10.91911384236453, 7,8.485281373797825,8.485281374060856,-6.044464322815054,-6.839106698131189, 7.5,8.485281374254145,8.485281374165625,-6.561675225100206,-4.844985154136384, 8,8.485281374248144,8.485281374260301,-9.939950823417254,-7.496878050831595, 8.5,8.48528137423595,8.485281374235834,-10.612692408264826,-12.418012796399863, 9,8.485281374238877,8.485281374238541,-7.261579601865494,-9.460068328198169, 9.5,8.485281374238578,8.485281374238657,-5.609690960477009,-5.547003194570313, 10,8.485281374238559,8.485281374238552,-7.564023040689936,-4.8184170397861195, ・dt=1e-3の場合、再現性が改善する 0,1,1,1,1, 0.5,1.424065299319062,-8.31093036476876,1.1982729919017479,-8.867197733337045, 1,-9.657031732204748,-8.349898928788475,-9.378570010918958,-8.357033792281806, 1.5,-9.899109831324854,-10.981836017099024,-9.672324278664984,-10.4319446298588, 2,-7.936611132655565,-9.562716397681724,-8.173499930210461,-9.56202368140192, 2.5,-6.623601079261224,-6.851281230459478,-6.959573599588022,-7.272469238587608, 3,-7.428423138226191,-5.8427878888642715,-7.456658266568281,-6.190996132824, 3.5,-9.780708645600205,-8.19962260010638,-9.440029006089206,-7.907954146669173, 4,-10.097871845892818,-11.360669556779794,-10.09069843044153,-10.930443911886044, 4.5,-7.7943760001249185,-9.619436494278556,-8.16045155213845,-9.956511240539381, 5,-6.3244974834629,-6.530279163772791,-6.512113702205631,-6.974042785103014, 5.5,-7.326268249826981,-5.4548631457194805,-7.062875222266096,-5.494495987755652, 6,-10.11165543413261,-8.40431517952932,-9.742121126780857,-7.706838552789133, 6.5,-10.150309659371128,-11.882555512309164,-10.464495656102148,-11.832252734547433, 7,-7.344746781343069,-9.2666415336227,-7.664493513190766,-9.841657380399884, 7.5,-5.932754897154663,-5.865106678257319,-5.7641286925570565,-6.010621413146083, 8,-7.534023075768873,-5.097187645426048,-7.012491606627554,-4.585886053449459, 8.5,-10.800316776867799,-9.456021549738772,-10.897293146993633,-8.935379986258638, 9,-9.711940724811386,-12.261944306401968,-9.981836816121655,-12.930829355294506, 9.5,-6.394634950585179,-8.072858428304484,-5.876031587809749,-7.71825674582792, 10,-5.5873779487212065,-4.734288502051793,-4.902687553795511,-3.7438729353865527, ・dt=1e-4の場合 0,1,1,1,1, 0.5,1.221151023207788,-8.810415963782997,1.1982729680518367,-8.867197729737649, 1,-9.405922103750052,-8.353560928731477,-9.378570010924973,-8.357033788427023, 1.5,-9.69914846586722,-10.488834732998349,-9.672324282181464,-10.431944632611662, 2,-8.15288430836313,-9.570016283145065,-8.173499932242123,-9.562023686798257, 2.5,-6.922521479260946,-7.230683555730671,-6.959573597294451,-7.27246923992412, 3,-7.446978291850581,-6.148275520785307,-7.456658260660321,-6.190996127653822, 3.5,-9.473921184162828,-7.927047084053216,-9.44002900312554,-7.907954136794917, 4,-10.1008045563268,-10.984178280080702,-10.090698436258997,-10.930443913833617, 4.5,-8.123277763605877,-9.931141795263137,-8.160451556821451,-9.95651125035683, 5,-6.48345119797466,-6.921902346045805,-6.5121136994200075,-6.97404278841702, 5.5,-7.081279834410035,-5.475054525286805,-7.062875212682948,-5.494495980662688, 6,-9.789784479401302,-7.775519667363902,-9.742121121485903,-7.706838536376619, 6.5,-10.4395147428828,-11.862578070722492,-10.464495665237356,-11.832252739274068, 7,-7.61624789132691,-9.77239548904484,-7.664493517737282,-9.841657392634252, 7.5,-5.765530745751043,-5.971969347245796,-5.764128686374217,-6.010621413751659, 8,-7.072926511613961,-4.622026044702504,-7.012491593513374,-4.585886040703437, 8.5,-10.915313145584335,-9.03579341104503,-10.89729314764603,-8.935379970921547, 9,-9.931757116419167,-12.86292491511394,-9.981836823753804,-12.930829370175513, 9.5,-5.900778896603505,-7.715560359560663,-5.87603158063658,-7.718256743244244, 10,-4.970644316069031,-3.816535259108012,-4.902687541135751,-3.74387292180464, |
|
目次
公転軌道 |
地球の公転軌道について記述する
前提を列挙する ・太陽を焦点位置の極とする平面極座標(距離r,真近点角θ)の楕円軌道を示す r(θ)=p/(1+er*cos(θ)) ・parameter 近日点距離rmin=p/(1+er)=147098074000[m] 遠日点距離rmax=p/(1-er)=152097701000[m] 楕円の離心率er=(rmax-rmin)/(rmax+rmin)=0.016710219253597416 円錐曲線の半直弦p=rmax*(1-er)=149556115068.3219[m] 楕円の長半径a=p/(1-er^2)=149597887500[m] 楕円の短半径b=p/sqrt(1-er^2)=149576999825.9354[m] 楕円の焦点距離c=a*er=2499813500[m] 楕円の扁平率f=1-b/a=0.0001396254613862391 楕円面積A=pi*a*b=7.029754388347137e+22[m^2] 太陽質量M=1.9884e30[kg] 地球質量m=5.9724e24[kg] 重力定数G=6.67430e-11[N*m^2/kg^2] m3_s2=G*(M+m)/(4*pi^2)=3361638785675266600[m^3/s^2] 恒星年の公転周期T=sqrt(a^3/m3_s2)=31558232.27154487[s] 地球の公転周期Te=60*60*24*365.25=31557600[s] 平均角速度n=2*pi/T=1.9909813873969582e-7[rad/s] 面積速度vA=n*a*b/2=A/T=2227550113662627.2[m^2/s] ・各天体の影響を記述する定数(太陽のみを想定) 定数alpha=G*M 定数beta=(n*a*b)^2 ・Kepler's laws(角運動量の保存則) r*(r*θ')/2=vA ・地球の力学的energy保存則 力学E0=K+P 運動K={(r')^2+(r*θ')^2}*m/2 位置P=-G*(M*m/r)※無限遠で最大値0に漸近 ・運動方程式 m*(r"-r*(θ')^2)=-G*M*m/r^2 r*θ"+2*r'*θ'=0 ・厳密構成の運動方程式 r'=v θ'=w ・Ver.2.358.86以降、遠心力項のwを残して記述(小数点以下の演算結果に影響あり) v'=-alpha/r^2+r*w^2 w'=-2*v*w/r ・w消去可能(非多体問題)の場合、最小構成の時間発展方程式 r'=v θ'=2*vA/r^2 v'=-alpha/r^2+beta/r^3 ・初期値 r=rmin θ=0 v=0 w=2*vA/rmin^2 ・時間tの従属変数 kT=t/T ・平均近点角 Mt=n*t ・Kepler方程式 Mt-(Et-er*sin(Et))=0 ・初期値 Et0=Mt ・楕円中心の離心近点角Etに対する(r,θ)の導出 y^2+(x-a*er)^2=r^2 x=a*cos(Et) y=b*sin(Et) b^2=a^2*(1-er^2) r=a*(1-er*cos(Et)) θ=2*atan(sqrt((1+er)/(1-er))*tan(Et/2)) ・基準値に対する変化率 θ方向の初速||面積速度kw r方向の重力kalpha r方向の遠心力kbeta ・月parameter 近地点距離rmmin=pm/(1+erm)=363304000[m] 遠地点距離rmmax=pm/(1-erm)=405495000[m] 楕円の離心率erm=(rmmax-rmmin)/(rmmax+rmmin)=0.05487910364087363 円錐曲線の半直弦pm=rmmax*(1-erm)=383241797.8691439[m] 楕円の長半径am=pm/(1-erm^2)=384399500[m] 質量mm=7.347673e22[kg] m3_s2m=G*(m+mm)/(4*pi^2)=10221279754278.992[m^3/s^2] 公転周期Tm=sqrt(am^3/m3_s2m)=2357336.516077939[s] 軌道傾斜角im=5.1454[deg] 解法を列挙する ・4次精度のODE高階行列関数 kT=1; kw=1; kalpha=1; kbeta=1; rmin=147098074000; rmax=152097701000; er=(rmax-rmin)/(rmax+rmin); p=rmax*(1-er); a=p/(1-er^2); b=p/sqrt(1-er^2); c=a*er; f=1-b/a; A=pi*a*b; M=1.9884e30; m=5.9724e24; G=6.67430e-11; m3_s2=G*(M+m)/(4*pi^2); T=sqrt(a^3/m3_s2); Te=60*60*24*365.25; n=2*pi/T; vA=n*a*b/2; alpha0=G*M; beta0=(n*a*b)^2; alpha=alpha0*kalpha; beta=beta0*kbeta; r0=rmin; theta0=0; v0=0; w0=2*vA/r0^2; w0=w0*kw; dt=T/1e4; t=T*kT; ・Ver.2.358.86以降、遠心力項のwを残して記述(小数点以下の演算結果に影響あり) x1=_otdummy(=<{v,w,-alpha/r^2+r*w^2,-2*v*w/r},=<{r,theta,v,w},=<{r0,theta0,v0,w0},N=round(t/dt),dt,N); r1=x1[0]; t1=x1[1]; zt1=r1*e^(i(t1)); ・最小構成の時間発展方程式 x1=_otdummy(=<{v,2*vA/r^2,-alpha/r^2+beta/r^3},=<{r,theta,v},=<{r0,theta0,v0},N=round(t/dt),dt,N); ・円錐曲線の方程式 zt2=(p/(1+er*cos(t1)))*e^(i(t1)); ・Kepler方程式 Mt=n*t; Et0=Mt; Newton(=<Mt-(Et-er*sin(Et))=0,=<{Et},=<{Et0},,20,1e-10,1); r3=a*(1-er*cos(Et)); t3=2*atan(sqrt((1+er)/(1-er))*tan(Et/2)); zt3=r3*e^(i(t3)); ・座標系の変換 x_o4=real(zt1); y_o4=imag(zt1); x_eq=real(zt2); y_eq=imag(zt2); x_Keq=real(zt3); y_Keq=imag(zt3); test caseを示す(厳密構成の運動方程式) ・index kT,0,x_Keq,y_Keq,x_o4,y_o4, ・平面直交座標(x,y)が地球の公転軌道を表す 0,0,147098074000,0,147098074000,0, 0.1,0,117645979454.41016,89119571482.18962,117646073297.56575,89119593954.0389, 0.2,0,41450127214.54836,142976295065.944,41450492075.00406,142976518853.716, 0.3,0,-50971439067.87596,141507725745.10355,-50970826324.21445,141508578479.43475, 0.4,0,-124373455351.08269,86742387417.0788,-124373124876.82574,86744300802.14795, 0.5,0,-152097701000,0.000018626596268732117,-152098630190.86963,2847237.163415004, 0.6,0,-124373455351.08261,-86742387417.07892,-124376437732.5601,-86739647462.52522, 0.7,0,-50971439067.87596,-141507725745.10355,-50976274874.828735,-141506712606.37128, 0.8,0,41450127214.548416,-142976295065.94394,41444929811.39818,-142978228089.31668, 0.9,0,117645979454.4102,-89119571482.18958,117642576260.75374,-89124306965.08633, 1,0,147098074000,-0.0000366357988125792,147098073884.09283,-5888056.317206092, ・rmaxのみ変更rmax=252097701000(er=0.26302790153528055) 0,0,147098074000,0,147098074000,0, 0.1,0,83557972868.06361,140897388150.65994,83558183078.02698,140897479453.7757, 0.2,0,-42229087824.4498,192314576944.42972,-42228485945.3599,192315282374.82703, 0.3,0,-155084162929.37552,165189573903.43307,-155083587063.4741,165191479182.0332, 0.4,0,-227490834971.59644,92627001386.56705,-227491097087.5838,92630308738.87328, 0.5,0,-252097701000,0.00003087306426020565,-252099755868.8234,4417821.374398763, 0.6,0,-227490834971.59644,-92627001386.56705,-227495618215.9173,-92622358230.52377, 0.7,0,-155084162929.37567,-165189573903.43295,-155092327715.35623,-165186426537.96497, 0.8,0,-42229087824.4498,-192314576944.42972,-42240196066.38786,-192315864253.44543, 0.9,0,83557972868.06361,-140897388150.65994,83547870672.60117,-140906748102.49075, 1,0,147098074000,-0.00004716597138408846,147098073382.89954,-15142709.324563585, ・rmaxのみ変更rmax=552097701000(er=0.5792363762495562) 0,0,147098074000,0,147098074000,0, 0.1,0,-62626443439.11277,261174554166.06073,-62625796112.305145,261175346811.72348, 0.2,0,-288122823089.16315,276298693685.8214,-288122226663.3176,276301799167.0267, 0.3,0,-438583213031.365,210183676429.1171,-438584031544.3952,210189493827.63293, 0.4,0,-524255815053.5066,111446835784.8594,-524259422245.3567,111455230501.72232, 0.5,0,-552097701000,0.00006761246823462625,-552105583152.8054,10437879.703500373, 0.6,0,-524255815053.5066,-111446835784.8594,-524269738526.3361,-111435439117.1665, 0.7,0,-438583213031.3652,-210183676429.11697,-438605472773.4481,-210173490276.0452, 0.8,0,-288122823089.16296,-276298693685.8215,-288156565897.7836,-276294727061.0847, 0.9,0,-62626443439.11253,-261174554166.06073,-62674042096.824776,-261192512879.90536, 1,0,147098074000,-0.00006979949972966329,147098060786.14868,-78353321.71765932, ・rmaxのみ変更rmax=952097701000(er=0.7323532761941338) 0,0,147098074000.00003,0,147098074000,0, 0.1,0,-277582752682.8333,364440230900.0082,-277581891691.2515,364442871797.7403, 0.2,0,-600689109629.1072,349055425649.00574,-600689989513.7448,349062938394.4549, 0.3,0,-802814360557.1411,256416905855.70325,-802819509259.686,256429424097.47037, 0.4,0,-915669937800.7218,133978368871.92062,-915681811193.4048,133995478709.32758, 0.5,0,-952097701000.0001,0.0001165983402005204,-952119070078.7697,20810323.929560415, 0.6,0,-915669937800.7218,-133978368871.92062,-915704324079.7625,-133955496277.04993, 0.7,0,-802814360557.141,-256416905855.70364,-802866821303.7648,-256395175295.65317, 0.8,0,-600689109629.1061,-349055425649.00574,-600768116573.6425,-349042367819.66956, 0.9,0,-277582752682.83374,-364440230900.00806,-277705594000.67816,-364462522337.94775, 1,0,147098074000.00003,-0.00009166110718503652,147097931599.78604,-269396950.9766738, test caseを示す(厳密構成の運動方程式) ・index kT,x_eq,y_eq,x_o4,y_o4, ・平面直交座標(x,y)が地球の公転軌道を表す 0,147098073999.99997,0,147098074000,0, 0.1,117646002546.9667,89119540358.84032,117646073297.56575,89119593954.0389, 0.2,41450402656.69341,142976210420.25388,41450492075.00406,142976518853.716, 0.3,-50970620178.47929,141508006164.01346,-50970826324.21445,141508578479.43475, 0.4,-124372435453.38469,86743819962.30083,-124373124876.82574,86744300802.14795, 0.5,-152097700972.89758,2847219.768755107,-152098630190.86963,2847237.163415004, 0.6,-124375748282.34204,-86739166642.60507,-124376437732.5601,-86739647462.52522, 0.7,-50976068701.38623,-141506140282.75314,-50976274874.828735,-141506712606.37128, 0.8,41444840400.379585,-142977919635.9288,41444929811.39818,-142978228089.31668, 0.9,117642505503.85724,-89124253360.68932,117642576260.75374,-89124306965.08633, 1,147098073884.093,-5888056.317206098,147098073884.09283,-5888056.317206092, ・kwのみ変更kw=2 0,147098073999.99997,0,147098074000,0, 0.1,40313864704.12989,143320548665.74713,39963981393.632774,142076672188.0772, 0.2,-128175044230.06297,81138311004.42026,-125780362967.34627,79622412225.38794, 0.3,-116707901382.4842,-96609697705.47668,-115862188780.14392,-95909624806.47014, 0.4,51374601374.660934,-139540806772.84842,52389537822.20742,-142297520147.24472, 0.5,147098073898.60037,-5507256.735869929,152098630110.9206,-5694474.325832261, 0.6,51385053462.16438,139536772070.5741,52400277078.75906,142293624829.2025, 0.7,-116700407079.7279,96618553997.54425,-115854914689.94438,95918554278.93999, 0.8,-128181477110.87065,-81128349023.08505,-125786665081.72433,-79612629665.4651, 0.9,40302518612.32475,-143323936611.14822,39952698717.83794,-142079906061.46906, 1,147098073536.37192,-11776112.625443231,147098073530.56128,-11776112.624978054, ・kwのみ変更kw=0.5 0,147098073999.99997,0,147098074000,0, 0.1,139556959168.63452,46891226700.466225,139904112535.889,47007870451.81143, 0.2,117995800207.00056,88646151463.3724,119018707817.5935,89414626466.91138, 0.3,85167892487.04904,121201478012.45401,86476180976.15123,123063288771.36153, 0.4,44616807517.52976,141964512424.33505,45463713511.03606,144659250195.30017, 0.5,1399820.832204594,149556091670.45782,1423618.581769861,152098630210.8569, 0.6,-45063414182.83178,143394995192.56958,-45461005553.438515,144660159266.58865, 0.7,-86817865319.67094,123554563734.21631,-86473877545.88696,123065018648.49815, 0.8,-121189550817.62807,91049210520.317,-119017034772.77872,89417008161.35355, 0.9,-144048300037.90366,48403507201.33528,-139903233358.63858,47010670459.72132, 1,-152097700969.02,3044090.942244757,-147098073972.4757,2944028.1591926794, ・rmaxのみ変更rmax=252097701000(er=0.26302790153528055) 0,147098074000,0,147098074000,0, 0.1,83558074667.10547,140897296649.11166,83558183078.02698,140897479453.7757, 0.2,-42228322695.23485,192314538907.6343,-42228485945.3599,192315282374.82703, 0.3,-155082630157.18475,165190459907.40613,-155083587063.4741,165191479182.0332, 0.4,-227489357066.74847,92629600233.48889,-227491097087.5838,92630308738.87328, 0.5,-252097700947.47586,4417785.36375123,-252099755868.8234,4417821.374398763, 0.6,-227493878139.49948,-92621649777.4002,-227495618215.9173,-92622358230.52377, 0.7,-155091370727.45456,-165185407265.03223,-155092327715.35623,-165186426537.96497, 0.8,-42240032760.892845,-192315120738.01846,-42240196066.38786,-192315864253.44543, 0.9,83547762257.46626,-140906565256.12994,83547870672.60117,-140906748102.49075, 1,147098073382.89758,-15142709.324563384,147098073382.89954,-15142709.324563585, ・kalphaのみ変更1.5 0,147098073999.99997,0,147098074000,0, 0.025,145176982934.70328,23894189094.511765,144235140747.86908,23739174471.294758, 0.05,139263871802.59872,47769740467.03764,135651613121.42142,46530677833.87866, 0.075,128886639964.42787,71524114308.42549,121373408022.10658,67354735229.130585, 0.1,113181883376.86172,94840711884.6251,101482636303.83882,85037332688.10573, 0.125,90783204642.07315,116935825123.62224,76197627042.21265,98148467282.8321, 0.15,59717053231.46555,136027281303.16985,46041966660.76375,104877304083.29753, 0.175,17566782854.625797,148225244224.15234,12196741600.835241,102913835588.66182, 0.2,-37070127531.2521,145528368286.1656,-22798368169.277584,89500887647.74635, 0.225,-98996388311.39369,114299125171.0699,-53905204138.261475,62237802613.47277, 0.25,-145630307313.1074,43504724424.13959,-72997576096.23523,21806857997.415226, 0.275,-144102351122.4538,-48245198341.11205,-72420216639.6979,-24246153435.203117, 0.3,-95726872652.54117,-116980430835.63377,-52442245232.9137,-64085624771.2314, 0.325,-33816872641.402935,-146262758562.02115,-20940003121.376114,-90568476077.23497, 0.35,20174187856.673615,-147848950267.38904,14093806977.11165,-103288151257.49194, 0.375,61664639096.547874,-135119767307.35834,47787466770.44303,-104712060020.66525, 0.4,92200128556.5684,-115791640548.52454,77701002717.44228,-97582581692.36623, 0.425,114190715631.84859,-93597016473.47838,102702962444.57387,-84181019574.22856, 0.45,129576505487.87877,-70242407387.37112,122293107111.4408,-66294134249.45932, 0.475,139693366266.97638,-46476061118.57711,136263735886.55664,-45335021172.056786, 0.5,145380925151.96027,-22598062850.369175,144537304894.2855,-22466930216.670135, 0.525,147092456197.26797,1296272329.7016587,147089647482.11853,1296247577.5163705, 0.55,144961369596.75638,25190279639.631405,143916136767.1362,25008647061.65634, 0.575,138821333690.91516,49063111912.69887,135022718665.62317,47720581415.80769, 0.6,128181218128.33159,72804638816.00638,120437160649.14456,68406152704.116425, 0.625,112153505116.51373,96081038771.13014,100246365955.43747,85880284918.63054, 0.65,89340912916.4048,118071652342.42268,74679767533.97752,98695695638.74084, 0.675,57736721313.13496,136915491910.70355,44285293958.49709,105017096032.40569, 0.7,14921295956.333057,148559309932.41623,10295681990.533932,102505802195.29466, 0.725,-40349380399.99002,144710363092.91074,-24646177915.674988,88391874166.93732, 0.75,-102225813183.76715,111493411901.06221,-55332946036.8206,60349326183.32185, 0.775,-147005756694.44843,38692921316.92716,-73514743740.60791,19349583711.21276, 0.8,-142426707392.91986,-52907565282.22129,-71783576450.16469,-26665604553.72296, 0.825,-92422782285.26747,-119538263607.411,-50945606515.22678,-65892296149.0132, 0.85,-30591257887.345062,-146916200532.29977,-19072129051.359436,-91594949988.85127, 0.875,22743580602.92643,-147432112734.7784,15986337271.084253,-103629218279.87894, 0.9,63579888062.0425,-134193782232.84093,49521539814.12235,-104521774608.45015, 0.925,93592049434.77249,-114639483071.23749,79189780161.76295,-96998361688.79286, 0.95,115180262833.29309,-92350124393.89162,103907295542.1198,-83311597253.7434, 0.975,130250985370.46527,-68959590404.01472,123196238845.70583,-65224552013.57295, 1,140109918335.2375,-45182099795.28346,136859080593.3514,-44133782324.133865, ・kbetaのみ変更0.5 0,147098073999.99997,0,147098074000,0, 0.025,145176692438.46588,23895983920.933964,144218049674.7055,23738191980.06544, 0.05,139258479835.59644,47785734467.19015,135569318604.78456,46519820325.44201, 0.075,128852167956.39511,71587383804.7661,121134152954.42064,67299427219.16744, 0.1,113034164613.86891,95020555603.28502,100916433687.81165,84833958222.05579, 0.125,90264126710.55682,117347914772.5622,75018243307.48097,97527497831.58354, 0.15,58087827756.67877,136760526556.432,43828025533.123436,103187605412.7285, 0.175,12834299402.78972,148789144481.37424,8508158436.889433,98635817601.51228, 0.2,-49559651179.5788,141983340390.0874,-27643966912.8862,79197142645.38521, 0.225,-123765630009.42245,87589878596.65831,-55240644467.67176,39094224641.81833, 0.25,-141992712923.55493,-54041125520.88986,-50370027016.06038,-19170370763.54061, 0.275,20871153418.535454,-147740411868.2874,7110124828.906045,-50330365054.219734, 0.3,141883521377.29578,-39147828775.35926,59172789729.10452,-16326675698.40852, 0.325,131080205329.23872,67339735271.17512,68745763705.6266,35316709470.541534, 0.35,84710966222.84447,121530582707.16083,53205891593.48722,76331829243.93053, 0.375,37847508957.784485,144034117520.99426,27197287040.66858,103503172222.96748, 0.4,-2771650151.9831977,149576752880.9085,-2201700369.122022,118818456144.01561, 0.425,-36868177960.560555,145576180143.11697,-31546974624.227966,124565094206.16684, 0.45,-65330710057.85347,135744832839.3807,-59006817558.36976,122604982844.2338, 0.475,-89051312795.93001,122000854974.14311,-83496183822.5516,114390293568.98016, 0.5,-108697288176.08583,105349534381.88113,-104288364182.73656,101076400271.37773, 0.525,-124688592110.31223,86298031328.17513,-120825395516.27727,83624280225.07515, 0.55,-137205267982.67914,65059866430.970024,-132615810818.0463,62883641898.83788, 0.575,-146177579340.6412,41662245957.31706,-139172506808.04114,39665721893.10382, 0.6,-151238145846.0743,16011396886.577208,-139969529908.25003,14818402347.180075, 0.625,-151611761043.80762,-12046348505.054657,-134408922046.6908,-10679492844.195105, 0.65,-145897306123.6044,-42616660798.40887,-121798515453.47934,-35577394516.33991, 0.675,-131652673451.84377,-75481622612.32213,-101360039050.75269,-58113671488.77295, 0.7,-104630445770.37271,-109295587279.4147,-72344463727.73492,-75570075147.05667, 0.725,-57599248484.543304,-139061780778.65967,-34544468579.50608,-83400659611.16959, 0.75,19384930663.300655,-147967802529.80942,9651019545.650417,-73667539964.20953, 0.775,119200792148.38875,-86984924951.76099,47491876428.2738,-34656458505.65385, 0.8,121351933503.94661,83894617486.07384,41320763867.55731,28566414879.48242, 0.825,-50565966786.61371,141645927964.43512,-18797010850.66397,52654388200.18173, 0.85,-143884192531.85468,48880650069.62996,-66870386270.35764,22717352711.130413, 0.875,-147468203262.18307,-36923070403.53064,-84179628613.9133,-21076884949.4191, 0.9,-121329749997.66507,-90866209182.98355,-81291794669.57784,-60881005849.33341, 0.925,-88510879248.88019,-122382356460.4201,-66967785096.490166,-92595118437.34348, 0.95,-55882404887.5177,-139729644455.91727,-46346449562.843666,-115885723462.42686, 0.975,-25318372613.952385,-147826714869.01382,-22489482960.008232,-131309639674.41568, 1,2828700579.245502,-149482085023.15744,2641047530.765584,-139565599286.3702, ・kbetaのみ変更0.1 0,147098073999.99997,0,147098074000,0, 0.025,0,145162954533.47018,23980705942.470203,143432957443.8769,23694912975.385746, 0.05,0,139022886568.21747,48478829170.45809,132320713174.81544,46141706650.34631, 0.075,0,127504774866.8692,74005440507.67946,113398449393.53851,65817944535.95176, 0.1,0,107903650444.294,100934422061.62721,86031165615.4201,80474626622.23354, 0.125,0,73800911790.94273,128658866102.25687,49366758205.581856,86062231207.47318, 0.15,0,6833484264.867963,149285607992.6484,3350208520.668752,73189297951.77475, 0.175,0,-145854685261.69608,42759770788.28867,-32330787929.01624,9478317948.916527, 0.2,0,-3722932477.4566607,-149572000302.96667,-949881249.589849,-38162292604.48337, 0.225,0,132693715791.84297,-64039769740.546776,68405004000.10013,-33013173827.610023, 0.25,0,147098050340.3405,84124270.89598542,101111008414.15446,57824626.78953615, 0.275,0,141064993575.19897,42049735368.0845,114206282706.57396,34043484804.215767, 0.3,0,128530120001.87202,72174992096.25555,115160543603.5822,64667420556.89343, 0.325,0,112958331674.04399,95112659029.68936,107662215714.95146,90653247634.94218, 0.35,0,95346338482.22711,113146289132.4068,93867864422.57188,111391802740.04579, 0.375,0,75835970112.49373,127430362884.99501,75220111963.7641,126395510594.42781, 0.4,0,54132640212.70215,138444716851.75223,52824007502.22701,135097876861.07762, 0.425,0,29579273189.862072,146097564737.21176,27680983436.06633,136721556462.26155, 0.45,0,1058670147.505807,149534676937.86502,921210430.5483837,130118814106.91095, 0.475,0,-33273314669.91725,146378054834.64105,-25799217402.8165,113497536904.38956, 0.5,0,-76381686118.59444,130062569437.67195,-49254998085.55424,83871303897.48306, 0.525,0,-130394109527.00873,77594428250.02861,-60568367977.7387,36042792886.25769, 0.55,0,-74656204904.56468,-131027431812.35657,-14303033295.088774,-25102933134.329777, 0.575,0,136530788007.73053,-55219273152.42157,39294929966.69632,-15892660571.28024, 0.6,0,119916184899.08337,85975500491.53827,63840941655.98622,45771610523.99745, 0.625,0,73797926918.63635,128660635730.07281,51223965241.77903,89304784128.80902, 0.65,0,35387261715.92298,144700550191.80008,28625812295.210163,117052594293.8467, 0.675,0,3263955201.0484405,149465939677.38678,2903736759.069016,132970496387.51431, 0.7,0,-24525659460.434933,147946870370.4161,-23112667188.362995,139423234753.28357, 0.725,0,-49298449335.635544,142069624160.26816,-47840564082.83314,137868250430.95865, 0.75,0,-71901084941.78963,132506933130.1091,-70130152268.42126,129243270870.79932, 0.775,0,-92848096415.70398,119217221762.72206,-88917958868.4715,114170913894.12941, 0.8,0,-112348257222.52686,101538011035.83133,-102995166368.32846,93084882648.69772, 0.825,0,-130159384216.98589,77979891679.59708,-110741552792.2073,66346459328.43736, 0.85,0,-144989837482.10648,45558108957.77031,-109655304514.85268,34455437688.87712, 0.875,0,-152083917218.0378,-2030445227.7360249,-95247488838.9627,-1271632219.267789, 0.9,0,-129503013830.11284,-79044101193.68102,-57695893967.49226,-35215551718.42579, 0.925,0,120339057124.75626,-85370394001.38515,19345509152.965008,-13724004309.206694, 0.95,0,103709614569.67398,105337486775.28682,32530498346.535286,33041111507.26093, 0.975,0,-17881225692.77743,148784263612.26624,-9673390588.676538,80489353475.9983, 1,0,-75941275553.55077,130311690206.56801,-52738337906.89914,90496530394.55447, test caseを示す(最小構成の時間発展方程式) ・index kT,x_eq,y_eq,x_o4,y_o4, ・平面直交座標(x,y)が地球の公転軌道を表す 0,147098073999.99997,0,147098074000,0, 0.1,117646002546.96661,89119540358.84045,117646073297.56566,89119593954.03902, 0.2,41450402656.69291,142976210420.25403,41450492075.003555,142976518853.71616, 0.3,-50970620178.48008,141508006164.01318,-50970826324.21523,141508578479.43448, 0.4,-124372435453.38525,86743819962.29999,-124373124876.82632,86744300802.14711, 0.5,-152097700972.89758,2847219.7676068433,-152098630190.86963,2847237.1622667327, 0.6,-124375748282.34135,-86739166642.60599,-124376437732.55945,-86739647462.52614, 0.7,-50976068701.38534,-141506140282.7534,-50976274874.82786,-141506712606.37158, 0.8,41444840400.38047,-142977919635.92853,41444929811.39907,-142978228089.31644, 0.9,117642505503.85786,-89124253360.68848,117642576260.75436,-89124306965.0855, 1,147098073884.093,-5888056.316422202,147098073884.09283,-5888056.316422196, ・rmaxのみ変更rmax=252097701000(er=0.26302790153528055) 0,147098074000,0,147098074000,0, 0.1,83558074667.10545,140897296649.1117,83558183078.02693,140897479453.77573, 0.2,-42228322695.23472,192314538907.63434,-42228485945.35978,192315282374.82703, 0.3,-155082630157.18417,165190459907.4064,-155083587063.47363,165191479182.03363, 0.4,-227489357066.74765,92629600233.49033,-227491097087.58316,92630308738.8748, 0.5,-252097700947.47586,4417785.365990307,-252099755868.8234,4417821.376637858, 0.6,-227493878139.50116,-92621649777.39735,-227495618215.91855,-92622358230.52074, 0.7,-155091370727.45825,-165185407265.03,-155092327715.35928,-165186426537.96207, 0.8,-42240032760.89792,-192315120738.01874,-42240196066.392654,-192315864253.44437, 0.9,83547762257.4613,-140906565256.13443,83547870672.59554,-140906748102.49408, 1,147098073382.89758,-15142709.332271695,147098073382.89954,-15142709.332271896, ・kalphaのみ変更1.5 0,147098073999.99997,0,147098074000,0, 0.025,145176982934.70328,23894189094.51183,144235140747.86908,23739174471.294823, 0.05,139263871802.59866,47769740467.03783,135651613121.42136,46530677833.87884, 0.075,128886639964.42763,71524114308.4259,121373408022.10637,67354735229.13097, 0.1,113181883376.86122,94840711884.62572,101482636303.83836,85037332688.10628, 0.125,90783204642.07219,116935825123.62297,76197627042.21185,98148467282.8327, 0.15,59717053231.46406,136027281303.17053,46041966660.76259,104877304083.29803, 0.175,17566782854.624187,148225244224.15256,12196741600.83412,102913835588.66194, 0.2,-37070127531.25197,145528368286.16562,-22798368169.277504,89500887647.74637, 0.225,-98996388311.38782,114299125171.07483,-53905204138.25832,62237802613.4755, 0.25,-145630307313.10352,43504724424.15245,-72997576096.23329,21806857997.421677, 0.275,-144102351122.4571,-48245198341.1024,-72420216639.69954,-24246153435.198257, 0.3,-95726872652.55399,-116980430835.62357,-52442245232.92065,-64085624771.225716, 0.325,-33816872641.424587,-146262758562.0165,-20940003121.38947,-90568476077.23189, 0.35,20174187856.649506,-147848950267.3927,14093806977.094774,-103288151257.49425, 0.375,61664639096.5257,-135119767307.36887,47787466770.425735,-104712060020.67314, 0.4,92200128556.54959,-115791640548.53993,77701002717.42625,-97582581692.379, 0.425,114190715631.83386,-93597016473.49666,102702962444.56049,-84181019574.24487, 0.45,129576505487.86786,-70242407387.39171,122293107111.43033,-66294134249.47865, 0.475,139693366266.96915,-46476061118.59911,136263735886.54951,-45335021172.07821, 0.5,145380925151.95682,-22598062850.391777,144537304894.282,-22466930216.6926, 0.525,147092456197.26816,1296272329.6791878,147089647482.1187,1296247577.4939003, 0.55,144961369596.7601,25190279639.609375,143916136767.14,25008647061.634483, 0.575,138821333690.92233,49063111912.67824,135022718665.63023,47720581415.78766, 0.6,128181218128.342,72804638815.98761,120437160649.15453,68406152704.09889, 0.625,112153505116.52739,96081038771.11383,100246365955.44984,85880284918.6161, 0.65,89340912916.42151,118071652342.4097,74679767533.99164,98695695638.73016, 0.675,57736721313.15416,136915491910.69508,44285293958.511925,105017096032.39944, 0.7,14921295956.354265,148559309932.41373,10295681990.54859,102505802195.29318, 0.725,-40349380399.96756,144710363092.9166,-24646177915.661324,88391874166.94112, 0.75,-102225813183.74614,111493411901.08102,-55332946036.80935,60349326183.33217, 0.775,-147005756694.43964,38692921316.96002,-73514743740.60359,19349583711.229214, 0.8,-142426707392.93112,-52907565282.19151,-71783576450.17027,-26665604553.707916, 0.825,-92422782285.29857,-119538263607.3876,-50945606515.24375,-65892296149.00008, 0.85,-30591257887.390358,-146916200532.29108,-19072129051.38758,-91594949988.84541, 0.875,22743580602.881233,-147432112734.78613,15986337271.052408,-103629218279.88385, 0.9,63579888062.001564,-134193782232.86108,49521539814.09023,-104521774608.46536, 0.925,93592049434.73784,-114639483071.26656,79189780161.7333,-96998361688.81705, 0.95,115180262833.26544,-92350124393.92691,103907295542.0945,-83311597253.77496, 0.975,130250985370.44466,-68959590404.05446,123196238845.68602,-65224552013.610374, 1,140109918335.22397,-45182099795.32609,136859080593.33798,-44133782324.17544, ・kbetaのみ変更0.5 0,147098073999.99997,0,147098074000,0, 0.025,145176692438.46588,23895983920.933994,144218049674.7055,23738191980.06547, 0.05,139258479835.59644,47785734467.190155,135569318604.78455,46519820325.44202, 0.075,128852167956.39511,71587383804.76608,121134152954.42064,67299427219.16743, 0.1,113034164613.8689,95020555603.28506,100916433687.81163,84833958222.05583, 0.125,90264126710.5567,117347914772.56232,75018243307.48087,97527497831.58363, 0.15,58087827756.67797,136760526556.43239,43828025533.12282,103187605412.72876, 0.175,12834299402.787115,148789144481.37448,8508158436.887703,98635817601.51244, 0.2,-49559651179.58439,141983340390.0856,-27643966912.889297,79197142645.38414, 0.225,-123765630009.41975,87589878596.66208,-55240644467.67056,39094224641.82002, 0.25,-141992712923.60995,-54041125520.7478,-50370027016.0796,-19170370763.4901, 0.275,20871153418.371944,-147740411868.3133,7110124828.850212,-50330365054.22763, 0.3,141883521377.21005,-39147828775.6753,59172789729.0682,-16326675698.540173, 0.325,131080205329.40662,67339735270.842155,68745763705.71596,35316709470.36758, 0.35,84710966223.14685,121530582706.94392,53205891593.67895,76331829243.79689, 0.375,37847508958.14244,144034117520.894,27197287040.9269,103503172222.89961, 0.4,-2771650151.6103024,149576752880.90918,-2201700368.8258996,118818456144.0211, 0.425,-36868177960.19652,145576180143.20288,-31546974623.917744,124565094206.2454, 0.45,-65330710057.512924,135744832839.53827,-59006817558.064415,122604982844.38075, 0.475,-89051312795.62317,122000854974.36076,-83496183822.26674,114390293569.18811, 0.5,-108697288175.82028,105349534382.14876,-104288364182.48483,101076400271.63747, 0.525,-124688592110.0943,86298031328.48357,-120825395516.069,83624280225.37607, 0.55,-137205267982.51463,65059866431.31055,-132615810817.8897,62883641899.16815, 0.575,-146177579340.5355,41662245957.68139,-139172506807.94214,39665721893.451164, 0.6,-151238145846.03363,16011396886.954594,-139969529908.21304,14818402347.52941, 0.625,-151611761043.8382,-12046348504.676308,-134408922046.71744,-10679492843.859648, 0.65,-145897306123.7125,-42616660798.04524,-121798515453.56813,-35577394516.035934, 0.675,-131652673452.03476,-75481622611.99536,-101360039050.89763,-58113671488.52015, 0.7,-104630445770.64828,-109295587279.15727,-72344463727.92325,-75570075146.87637, 0.725,-57599248484.89062,-139061780778.5221,-34544468579.71304,-83400659611.08386, 0.75,19384930662.934517,-147967802529.86353,9651019545.467737,-73667539964.23346, 0.775,119200792148.136,-86984924952.11458,47491876428.17173,-34656458505.793724, 0.8,121351933504.26471,83894617485.60432,41320763867.66713,28566414879.323586, 0.825,-50565966786.0039,141645927964.64203,-18797010850.438553,52654388200.2622, 0.85,-143884192531.60495,48880650070.352196,-66870386270.2434,22717352711.466694, 0.875,-147468203262.37308,-36923070402.784836,-84179628614.02,-21076884948.99293, 0.9,-121329749998.13031,-90866209182.37524,-81291794669.8854,-60881005848.92273, 0.925,-88510879249.50414,-122382356459.98172,-66967785096.95762,-92595118437.0054, 0.95,-55882404888.2275,-139729644455.64615,-46346449563.4287,-115885723462.1929, 0.975,-25318372614.70132,-147826714868.89825,-22489482960.671604,-131309639674.30205, 1,2828700578.4905634,-149482085023.18433,2641047530.0605044,-139565599286.38354, ・kbetaのみ変更0.1 0,147098073999.99997,0,147098074000,0, 0.025,145162954533.47015,23980705942.47039,143432957443.87686,23694912975.38593, 0.05,139022886568.2173,48478829170.45858,132320713174.81526,46141706650.34678, 0.075,127504774866.86862,74005440507.68042,113398449393.538,65817944535.95262, 0.1,107903650444.29156,100934422061.62985,86031165615.41814,80474626622.23563, 0.125,73800911790.92825,128658866102.26541,49366758205.572105,86062231207.47876, 0.15,6833484264.686319,149285607992.65982,3350208520.5796294,73189297951.77884, 0.175,-145854685272.05933,42759770753.554955,-32330787931.27656,9478317941.2065, 0.2,-3723061256.8467317,-149571999250.11707,-949914093.1249884,-38162291786.974884, 0.225,132693660277.7089,-64039886902.861206,68404974951.29937,-33013234018.160297, 0.25,147098050413.71948,83993716.55452698,101111008465.43588,57734887.4556947, 0.275,141065030509.93604,42049609301.740654,114206313087.8074,34043382883.586555, 0.3,128530183754.84512,72174876388.25569,115160601557.30424,64667317352.07901, 0.325,112958416135.50589,95112556529.66833,107662297245.39177,90653150807.12749, 0.35,95346439481.50429,113146201815.00438,93867964926.4119,111391718047.1938, 0.375,75836084462.40714,127430292609.76704,75220226354.3189,126395442518.59857, 0.4,54132765132.34455,138444665766.09354,52824130143.77331,135097828907.49919, 0.425,29579405804.81425,146097535626.61105,27681107951.79574,136721531252.44093, 0.45,1058806803.9091433,149534673686.6919,921329357.297437,130118813264.88335, 0.475,-33273179811.727013,146378083178.30472,-25799113224.768166,113497560585.13615, 0.5,-76381565034.26578,130062638200.1861,-49254920664.63166,83871349364.32553, 0.525,-130394036186.62662,77594549098.74965,-60568334400.15863,36042849311.881424, 0.55,-74656331461.52693,-131027362137.2198,-14303057340.966644,-25102919433.565292, 0.575,136530675782.83673,-55219555631.53874,39294897166.890015,-15892741669.23481, 0.6,119916362844.65125,85975247194.38351,63841037677.132996,45771476596.13394, 0.625,73798196450.05496,128660475938.03633,51224153882.00385,89304675927.17055, 0.65,35387567531.64235,144700470141.8086,28626060660.69309,117052533554.51472, 0.675,3264273328.958136,149465927412.6905,2904019880.8304763,132970490204.55502, 0.7,-24525342653.101795,147946917522.13858,-23112369449.077484,139423284110.2181, 0.725,-49298143453.18094,142069724891.38983,-47840268872.20482,137868352869.29465, 0.75,-71900798194.02844,132507083273.57314,-70129874812.27246,129243421424.0313, 0.775,-92847837157.33405,119217418185.30872,-88917713133.44252,114171105275.69891, 0.8,-112348035328.18967,101538251023.672,-102994965468.75789,93085104936.56252, 0.825,-130159212947.4345,77980171983.1191,-110741409162.31299,66346699066.30179, 0.85,-144989736889.15472,45558423488.71889,-109655229649.5749,34455675948.6177, 0.875,-152083921726.61295,-2030113143.9160638,-95247491615.42476,-1271424240.3684185, 0.9,-129503190375.91267,-79043817609.24973,-57695971499.915276,-35215424691.776695, 0.925,120338866226.0798,-85370668606.81783,19345478046.154053,-13724048157.608175, 0.95,103709990230.37575,105337108109.43132,32530617561.10511,33040994134.594463, 0.975,-17880681009.149597,148784319905.27673,-9673096513.089552,80489388818.11534, 1,-75940792684.72919,130311962266.09206,-52738005394.1805,90496724170.9786, |
|
目次
Newton法 |
Newton法について記述する
連立方程式{f[i]}=0の解法を一般化する ・近似解の列vector{x}の各要素を表す添字をjとする ・方程式の列vector{f}の各要素を表す添字をiとする ・方程式の全微分dfを次のtensorで表記する {df[i]}=(df[i]/dx[j]){dx[j]} ・左辺の全微分を単純に仮定すると {df[i]}={0-f[i]} ・連立線形方程式A*x=bに一般化されたNewton-Raphson法が導出される ・ここで、前置単項の符号はscalar倍||zeros行列との差||和で定義される (df[i]/dx[j]){dx[j]}={-f[i]} A=(df[i]/dx[j]) x={dx[j]} b={-f[i]} ・Jacobi行列Aがfull-rankであれば求解の必要十分条件を満たす ・求解して得られたdx(解の修正vector)から近似解を修正する ・f||dxのnormが許容誤差範囲内に収束するまで近似解の修正を反復する ・fが線形の場合、反復1回で厳密解が得られる Newton((x,y)=<(2x+y+2=0,2x-3y=2)) -> (-0.5,-1) Newton((x,y)=<(2x+y+1=0,y)) -> (-0.5,0) Newton((x)=<2x+1=0) -> -0.5 上記の反復1回の処理をまとめたNewton高階行列関数について記述する ・scalar倍の符号位置を変えて次の連立線形方程式をGaussの消去法で解く A=(df[i]/dx[j]) x={-dx[j]} b={f[i]} ・ここで、Jacobi行列Aは解析的に陰の前提でJacobi高階行列関数から得る(Euler前進差分のsecant法) ・最後に、符号付の解の修正vectorをmdxとして近似解のvectorを一度に修正する x=x-mdx 留意事項を列挙する ・Newton高階行列関数の反復過程でJacobi行列の対角要素=0の場合、 ・Ver.2.408.86以降、収束計算のretry機能を追加 近似解の列vector{x}の各要素初期値の係数倍:区間[-1,1)の乱数*retry回数 Ver.2.834.140~2.836.141以降、機能を強化 連立方程式の列挙順序:昇順 ⇒ Fisher-Yates shuffle(Ver.2.840.146以降、次の暫定対策) 電気回路計算:switching回路 CFD解析:多少複雑な迷路 |
|
目次
Gauss の消去法 |
Gaussの消去法について記述する
実装 ・前処理(scalingを含む):なし Ver.2.840.146以降、修正 ・pivot選択:部分選択法 処理順:前進消去の直前 ⇒ 前進消去の各step Ver.2.871.164以降、修正 ・前進消去 ・後退代入 ・Ver.2.124.34以降、座標形式に対応 full-rank2元1次の連立線形方程式A*x=bを一例に示す A=(1,2:3,4); b={5,6}; x=Gauss(A,b); x -> (-3.9999999999999982:4.499999999999999) x=Gauss((1,2:3,4),{5,6}); x -> (-3.9999999999999982:4.499999999999999) ・解のdouble-check A*x -> (5:6.000000000000002) ・Ver.2.224.51以降、欠損要素||変数名symbol要素残存時のerror処理を追加 clear; x=Gauss((1,2:3,a),{5,6}); x -> [MyErr]Invalid irregular matrix clear; x=Gauss((1,2:3,4),a); x -> [MyErr]Invalid irregular matrix ・行列操作を駆使して演算内容を以下に示す ・pivot選択 A=(1,2:3,4); A=(A[1]:A[0]); A -> (3,4:1,2) b={5,6}; b=(b[1]:b[0]); b -> (6:5) ・前進消去 k=A[1][0]/A[0][0]; k -> 0.3333333333333333 ・行vectorの左から無次元係数kを積 A[1]=A[1]-k(A[0]); A -> (3,4:0,0.6666666666666667) b[1]=b[1]-k(b[0]); b -> (6:3) ・後退代入 x={,}; x -> (0:0) x[1]=b[1]/A[1][1]; x -> (0:4.499999999999999) x[0]=(b[0]-A[0]x)/A[0][0]; x -> (-3.9999999999999982:4.499999999999999) |
|
目次
連立 線形方程式 の解法 |
連立線形方程式の解法について記述する
連立方程式の解法には直接法と反復法の2種類が存在し、特徴を列挙する ・直接法は解を厳密に解くため、線形方程式のみ適用可 ・反復法は解の修正を繰り返して近似的に解くため、非線形方程式に拡張可 full-rank2元1次の連立線形方程式A*x=bを一例に示す A=(1,2:3,4); b={5,6}; 直接法 ・式変数を使用してGaussの消去法のalgorithmを一般化する clear; A=(1,2:3,4); b={5,6}; sizeA=size(A); x=zeros(sizeA,1), compare=<switch(abs(A[ir][ir])<abs(A[ir_comp][ir]),=<{ir_pivot=ir_comp}); proc=<{w=A[ir],A[ir]=A[ir_pivot],A[ir_pivot]=w,w=b[ir],b[ir]=b[ir_pivot],b[ir_pivot]=w}; pivotting=<{ir_comp=ir+1,ir_pivot=ir,compare,switch(ir<>ir_pivot,=<proc),ir=ir+1,=<A}=>; ir=0; pivotting -> (3,4:1,2) pivotting -> [MyErr]Invalid reference of array forward=<{ir=ir+1,k=A[ir][ic]/A[ic][ic],A[ir]=A[ir]-k(A[ic]),b[ir]=b[ir]-k(b[ic]),=<A}=>; ic=0; ir=ic; forward -> (3,4:0,0.6666666666666667) forward -> [MyErr]Invalid reference of array ic=ic+1; ir=ic; forward -> [MyErr]Invalid reference of array backward=<{x[ir]=(b[ir]-A[ir]x)/A[ir][ir],ir=ir-1,=<x}=>; ir -> 1 backward -> (0:4.499999999999999) backward -> (-3.9999999999999982:4.499999999999999) backward -> [MyErr]Invalid reference of array ・実際には重複する演算や自明の演算は行わないが、ここでは簡潔に記述する 厳密な記述はstrict-mode式変数list-solvex_Gauss参照 ・さらに、総和高階関数を使用して反復処理を記述する ・dummy変数を使用するだけで総和は無次元の0を返す clear; A=(1,2:3,4); b={5,6}; sizeA=size(A); x=zeros(sizeA,1), compare=<switch(abs(A[ir][ir])<abs(A[ir_comp][ir]),=<{ir_pivot=ir_comp}); proc=<{w=A[ir],A[ir]=A[ir_pivot],A[ir_pivot]=w,w=b[ir],b[ir]=b[ir_pivot],b[ir_pivot]=w}; pivotting=<last{ir_pivot=ir,compare,switch(ir<>ir_pivot,=<proc)}; _sir(=<{_sir_comp(=<pivotting,ir+1,sizeA-1)},0,sizeA-2); A -> (3,4:1,2) forward=<last{k=A[ir][ic]/A[ic][ic],A[ir]=A[ir]-k(A[ic]),b[ir]=b[ir]-k(b[ic])}; _sic(=<{_sir(=<forward,ic+1,sizeA-1)},0,sizeA-2); A -> (3,4:0,0.6666666666666667) backward=<{x[ir]=(b[ir]-A[ir]x)/A[ir][ir]}; _sir(=<backward,sizeA-1,0); x -> (-3.9999999999999982:4.499999999999999) ・最後に、一連のalgorithmを一般化した式変数solvexを定義する ・pivot選択ありの場合 clear; solvex_pivotting=<{ compare=<switch(abs(A[ir][ir])<abs(A[ir_comp][ir]),=<{ir_pivot=ir_comp}), proc=<{w=A[ir],A[ir]=A[ir_pivot],A[ir_pivot]=w,w=b[ir],b[ir]=b[ir_pivot],b[ir_pivot]=w}, pivotting=<last{ir_pivot=ir,compare,switch(ir<>ir_pivot,=<proc)}, forward=<last{k=A[ir][ic]/A[ic][ic],A[ir]=A[ir]-k(A[ic]),b[ir]=b[ir]-k(b[ic])}, backward=<{x[ir]=(b[ir]-A[ir]x)/A[ir][ir]}, sizeA=size(A), x=zeros(sizeA,1), _sir(=<{_sir_comp(=<pivotting,ir+1,sizeA-1)},0,sizeA-2), _sic(=<{_sir(=<forward,ic+1,sizeA-1)},0,sizeA-2), _sir(=<backward,sizeA-1,0), =<x}=>; ・pivot選択なしの場合 clear; solvex_no_pivotting=<{ forward=<last{k=A[ir][ic]/A[ic][ic],A[ir]=A[ir]-k(A[ic]),b[ir]=b[ir]-k(b[ic])}, backward=<{x[ir]=(b[ir]-A[ir]x)/A[ir][ir]}, sizeA=size(A), x=zeros(sizeA,1), _sic(=<{_sir(=<forward,ic+1,sizeA-1)},0,sizeA-2), _sir(=<backward,sizeA-1,0), =<x}=>; test caseを示す ・pivot選択ありの場合 A=(1,2:3,4); b={5,6}; solvex_pivotting -> (-3.9999999999999982:4.499999999999999) ・pivot選択なしの場合(参考) A=(1,2:3,4); b={5,6}; solvex_no_pivotting -> (-4:4.5) 反復法 ・連立方程式と未知変数初期値(以降、初期値と省略する)を定義する clear; A=(1,2:3,4); b={5,6}; x0=0; x1=0; x=<{x0,x1}; x_initial=<{x0,x1}; ・連立方程式を展開しない場合 f=<{A*x=b}; || f=<{=b-A*x}; || f=<{b-A*x}; ・連立方程式を展開する場合 f=<{x0+2x1=5,3x0+4x1=6}; ・いずれの結果も以下に同じ ・続けて以降の処理を反復する J=Jacobi(=<f,=<x,=<x_initial); dx=Gauss(J,-f); x_next=x+dx; x0=x_next[0]; x1=x_next[1]; normf=max(normc(f),normc(-dx)); ・反復3回目のnormと近似解を示す normf -> infoLost[ri] 2.2204460494935903e-15 x0 -> infoLost[ri] -3.999999999999999-3.362471994400586e-26i x1 -> infoLost[ri] 4.499999999999999+6.466216308756395e-26i ・normがMachine epsilonに収束すれば収束判定条件を満たす ・その場合、近似解は厳密解にほぼ一致する Newton高階行列関数を使用して反復1回の処理を簡潔にまとめる clear; x=<{x0,x1}; x_initial=<{0,0}; f=<{x0+2x1=5,3x0+4x1=6}; run=<last(mdx=Newton(=<f,=<x,=<x_initial),max(normc(f),normc(mdx))); ・実行用の式変数runを定義してnormのみ表示する 反復を実行 run -> 6.020797289251035 run -> 2.0548659974995737e-10 ・反復3回目のnormと近似解は先述の通り一致する run -> infoLost[ri] 2.2204460494935903e-15 x -> ( infoLost[ri] -3.999999999999999-3.362471994400586e-26i: infoLost[ri] 4.499999999999999+6.466216308756395e-26i ) 再帰高階関数を使用して反復を実行 clear; x=<{x0,x1}; x_initial=<{0,0}; f=<{x0+2x1=5,3x0+4x1=6}; run=<last(mdx=Newton(=<f,=<x,=<x_initial),max(normc(f),normc(mdx))); _rn(=<run,,3) -> infoLost[ri] 2.2204460494935903e-15 x -> ( infoLost[ri] -3.999999999999999-3.362471994400586e-26i: infoLost[ri] 4.499999999999999+6.466216308756395e-26i ) rank落ち3元⇒実質2元1次の連立線形方程式A*x=bを一例に示す A=(i,2i,3i:4i,5i,6i:7i,8i,9i); b={10i,11i,12i}; ・Aの2行目を2倍して3行目を引くと1行目になる ・この場合、3階から2階へのrank落ちと呼ぶ ・本例では右辺bも成立するため、不定の解が得られる 直接法 ・解はalgorithmに従って一意に求まる A=(i,2i,3i:4i,5i,6i:7i,8i,9i); b={10i,11i,12i}; x=Gauss(A,b); x -> (-25.333333333333332:41.666666666666664:-16) A*x -> (10i:10.999999999999986i:12i) ・algorithmを以下に示す ・pivot選択は行列操作で示す clear; A=(i,2i,3i:4i,5i,6i:7i,8i,9i); A=(A[2]:A[1]:A[0]); b={10i,11i,12i}; b=(b[2]:b[1]:b[0]); sizeA=size(A); x=zeros(sizeA,1); forward=<last{k=A[ir][ic]/A[ic][ic],A[ir]=A[ir]-k(A[ic]),b[ir]=b[ir]-k(b[ic])}; _sic(=<{_sir(=<forward,ic+1,sizeA-1)},0,sizeA-2); A -> ( 7i,8i,9i: 0,0.4285714285714288i,0.8571428571428577i: 0,-1.1102230246251565e-16i,-2.220446049250313e-16i ) ・前進消去後、rank落ちの対角要素は限りなく0に近づく ・よって多くの場合、次の後退代入で解が発散する backward=<{x[ir]=(b[ir]-A[ir]x)/A[ir][ir]}; _sir(=<backward,sizeA-1,0); x -> (-25.333333333333332:41.666666666666664:-16) ・先述の式変数solvexを使用 ・pivot選択ありの場合 A=(i,2i,3i:4i,5i,6i:7i,8i,9i); b={10i,11i,12i}; solvex_pivotting -> (-25.333333333333332:41.666666666666664:-16) ・pivot選択なしの場合(参考) A=(i,2i,3i:4i,5i,6i:7i,8i,9i); b={10i,11i,12i}; solvex_no_pivotting -> (NaN:NaN:NaN) ・前進消去後、rank落ちの対角要素が0になる A=(i,2i,3i:4i,5i,6i:7i,8i,9i); b={10i,11i,12i}; sizeA=size(A); x=zeros(sizeA,1); forward=<last{k=A[ir][ic]/A[ic][ic],A[ir]=A[ir]-k(A[ic]),b[ir]=b[ir]-k(b[ic])}; _sic(=<{_sir(=<forward,ic+1,sizeA-1)},0,sizeA-2); A -> (i,2i,3i:0,-3i,-6i:0,0,0) ・よって次の後退代入で解が発散する backward=<{x[ir]=(b[ir]-A[ir]x)/A[ir][ir]}; ir=sizeA-1; A[ir][ir] -> 0 backward; x[ir] -> NaN 反復法 ・解が不定の場合、得られる近似解は初期値によって大きく異なる ・初期値がzeros-vectorの場合 clear; A=(i,2i,3i:4i,5i,6i:7i,8i,9i); b={10i,11i,12i}; x=<{x0,x1,x2}; x_initial=<{0,0,0}; f=<{A*x=b}; run=<last(mdx=Newton(=<f,=<x,=<x_initial),max(normc(f),normc(mdx))); _rn(=<run,,3) -> 0.000002904400992198821 x -> ( 338886.6528089325-469606.73307464283i: -677782.3056178652+939213.4661492857i: 338895.986142266-469606.7330746428i ) A*x -> (-2.3283064365386963e-10+10.000000000116415i:11i:12i) ・初期値が虚数単位vectorの場合 clear; A=(i,2i,3i:4i,5i,6i:7i,8i,9i); b={10i,11i,12i}; x=<{x0,x1,x2}; x_initial=<{i,i,i}; f=<{A*x=b}; run=<last(mdx=Newton(=<f,=<x,=<x_initial),max(normc(f),normc(mdx))); _rn(=<run,,3) -> 0.000011389894276669376 x -> ( -6.91661370055543-4.416691871261055i: 4.833227401110859+8.83338374252211i: 2.4167196327779044-4.416691871261055i ) A*x -> (10.000000000000002i:11.000000000000005i:12.000000000000007i) ・初期値が直接法による厳密解の場合 ・rank落ちの場合、近似解が厳密解に近づくとは限らない ・Jacobi行列の数値誤差が初期値の厳密解に上乗せして残る clear; A=(i,2i,3i:4i,5i,6i:7i,8i,9i); b={10i,11i,12i}; x=<{x0,x1,x2}; x_initial=<(-25.333333333333332:41.666666666666664:-16); f=<{A*x=b}; run=<last(mdx=Newton(=<f,=<x,=<x_initial),max(normc(f),normc(mdx))); _rn(=<run,,3) -> 0.00013856472352298855 x -> ( -25.33341533331434-0.00008200052251608464i: 41.66683066662869+0.0001640010450321693i: -16.000081999981045-0.00008200052251608478i ) A*x -> ( 3.2526065174565133e-19+9.999999999999915i: 6.505213034913027e-19+10.999999999999844i: 9.75781955236954e-19+11.999999999999773i ) rank落ち3元⇒実質2元1次の連立線形方程式A*x=bを一例に示す A=(i,2i,3i:4i,5i,6i:7i,8i,9i); b={10i,11i,12}; ・本例では右辺bが成立しないため、解が不能で発散する 直接法 ・解が17桁を超えて発散する A=(i,2i,3i:4i,5i,6i:7i,8i,9i); b={10i,11i,12}; x=Gauss(A,b); x -> ( infoLost[r ] 54043195528445890+54043195528445910i: -108086391056891790-108086391056891840i: 54043195528445900+54043195528445930i ) A*x -> (infoLost[r ] -32+32i:infoLost[r ] 64i:infoLost[r ] -64) 反復法 ・初期値に依らず、解が発散する clear; A=(i,2i,3i:4i,5i,6i:7i,8i,9i); b={10i,11i,12}; x=<{x0,x1,x2}; f=<{A*x=b}; run=<last(mdx=Newton(=<f,=<x),max(normc(f),normc(mdx))); run -> 234013055737.99323 run -> NaN |
|
目次
逆行列 の解法 |
逆行列の反復解法について記述する
任意の正方行列Aの逆行列Ainvを次の関係式から反復法で求解する Ainv*A=単位行列identity(size(A)) full-rank2階の場合 clear; A=(1,2:3,4); Ainv=<(x0,x1:x2,x3); x=<{x0,x1,x2,x3}; ・連立方程式を展開しない場合 f=<{Ainv*A=identity2}; || f=<{=identity2-Ainv*A}; || f=<{identity2-Ainv*A}; ・連立方程式を展開する場合 f=<{x0+3x1=1,2x0+4x1=0,x2+3x3=0,2x2+4x3=1}; ・いずれの結果も以下に同じ run=<last(mdx=Newton(=<f,=<x),max(normc(f),normc(mdx))); _rn(=<run,,3) -> infoLost[ri] 4.965068306494841e-16 Ainv -> ( infoLost[ri] -2-1.405479820560668e-34i, infoLost[ri] 1+7.02739910280334e-35i: infoLost[ i] 1.5000000000000002+2.2201233082568935e-28i, infoLost[ i] -0.5000000000000001+5.05296129055519e-28i ) Ainv*A -> ( infoLost[ri] 1+7.02739910280334e-35i, infoLost[ri] 0: infoLost[ i] -2.220446049250313e-16+1.7379007179922464e-27i, infoLost[ i] 1+2.4652091778734548e-27i ) symbolic高階行列関数を使用 ・逆行列Ainvと未知変数vectorを一般化して記述する Ainv=<(x0,x1,x2:x3,x4,x5:x6,x7,x8) || _eAinv(=<{x},3,3) -> 0 x=<{x0,x1,x2,x3,x4,x5,x6,x7,x8} || _ex(=<{x},3*3,1) -> 0 ・逆行列を解く式変数solveAinvを定義する solveAinv=<{ sizeA=size(A), _eAinv(=<{x},sizeA,sizeA), _ex(=<{x},sizeA*sizeA,1), f=<{Ainv*A=identity(sizeA)}, run=<last(mdx=Newton(=<f,=<x),max(normc(f),normc(mdx))), _rn(=<run,,3), =<Ainv}=>; full-rank3階の場合 clear; A=(i,2,3i:4,5i,6:7i,8,9i); Ainv=<(x0,x1,x2:x3,x4,x5:x6,x7,x8); x=<{x0,x1,x2,x3,x4,x5,x6,x7,x8}; f=<{Ainv*A=identity3}; run=<last(mdx=Newton(=<f,=<x),max(normc(f),normc(mdx))); _rn(=<run,,3) -> infoLost[ri] 3.4546432349907805e-16 Ainv -> ・式変数solveAinvを使用 A=(i,2,3i:4,5i,6:7i,8,9i); solveAinv -> ( infoLost[ri] -1.8979941071411976e-27+0.7750000000000002i, infoLost[ri] 0.05-4.672139890674269e-28i, infoLost[ri] 4.304317789445746e-28-0.22500000000000006i: infoLost[ri] 0.05000000000000003+8.567561244782949e-29i, infoLost[ri] 3.393936952792186e-29-0.1i, infoLost[ri] 0.05+8.5354798231355e-30i: infoLost[ri] 2.8820733759262382e-36-0.5583333333333333i, infoLost[ri] 0.05+4.64802404929633e-38i, infoLost[ri] -9.847979430502188e-37+0.10833333333333334i ) Ainv*A -> ( infoLost[ri] 1.0000000000000002-7.538276107988833e-28i, infoLost[ri] 1.983535962611336e-27, infoLost[ri] -4.623380245326983e-27i: infoLost[ri] -9.666493098090539e-30+5.551115123125783e-17i, infoLost[ri] 1+4.093319111203523e-28i, infoLost[ri] -1.302099385841768e-28: infoLost[ri] -3.82559126345344e-36i, infoLost[ri] -2.3466379950140902e-36, infoLost[ri] 1+6.192008328452557e-38i ) full-rank4階の場合 clear; A=(i+1,2-i,3i,4:5i,6-i,7,8i:9-5i,10i,-11+3i,12-5i:-13,14i,-15,16i); Ainv=<(x0,x1,x2,x3:x4,x5,x6,x7:x8,x9,x10,x11:x12,x13,x14,x15); x=<{x0,x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15}; f=<{Ainv*A=identity4}; run=<last(mdx=Newton(=<f,=<x),max(normc(f),normc(mdx))); _rn(=<run,,3) -> infoLost[ri] 2.9893669801409083e-16 Ainv -> ・式変数solveAinvを使用 A=(i+1,2-i,3i,4:5i,6-i,7,8i:9-5i,10i,-11+3i,12-5i:-13,14i,-15,16i); solveAinv -> ( 0.06841552622694629+0.2755281676127789i, infoLost[r ] 0.017370056945596502+0.04070708231511685i, 0.03704852337184109+0.014871122300002907i, infoLost[r ] -0.0771427485472948+0.029183958646809872i: infoLost[r ] -0.2463189713572816+0.22391026429285282i, 0.03674146878053252-0.07376715131162677i, infoLost[ i] 0.011750959713282166-0.06258676545881785i, infoLost[r ] -0.023736051458965405-0.035441311604425964i: 0.042729078026869684-0.37565683291263197i, infoLost[ri] 0.10071161649924316+0.02655781643708819i, 0.018188177584406696+0.012939541975857932i, 0.039537548991770054+0.015088101343933952i: infoLost[ i] 0.08721745526741176-0.29156760696583045i, infoLost[ i] 0.025823672107836676-0.04398405433866421i, 0.013931517721997284+0.007610078051463436i, infoLost[ri] 0.05862610643706584-0.005876821331234674i ) Ainv*A -> ( infoLost[r ] 1+5.551115123125783e-17i, infoLost[r ] 5.551115123125783e-17-2.220446049250313e-16i, infoLost[r ] 2.220446049250313e-16+5.551115123125783e-17i, infoLost[r ] 1.1102230246251565e-16+2.220446049250313e-16i: infoLost[ri] -5.551115123125783e-17-5.551115123125783e-17i, infoLost[ri] 1+1.1102230246251565e-16i, infoLost[ri] -1.1102230246251565e-16+1.1102230246251565e-16i, infoLost[ri] -1.1102230246251565e-16+5.551115123125783e-17i: infoLost[ri] -1.1102230246251565e-16+5.551115123125783e-17i, infoLost[ri] -2.7755575615628914e-17+1.1102230246251565e-16i, infoLost[ri] 0.9999999999999998, infoLost[ri] 0: infoLost[ri] -4.163336342344337e-17i, infoLost[ri] -1.1102230246251565e-16i, infoLost[ri] 2.220446049250313e-16-1.3877787807814457e-17i, infoLost[ri] 1-1.1102230246251565e-16i ) rank落ち3階⇒実質2階の場合 A=(i,2i,3i:4i,5i,6i:7i,8i,9i); ・rank落ちの場合、逆行列が一意に定まらず、不能となる ・行列式が0に漸近するため、逆行列を解く過程で発散する ・初期値がzeros-vectorの場合 clear; A=(i,2i,3i:4i,5i,6i:7i,8i,9i); Ainv=<(x0,x1,x2:x3,x4,x5:x6,x7,x8); x=<{x0,x1,x2,x3,x4,x5,x6,x7,x8}; f=<{ x0(i)+x1(4i)+x2(7i)=1,x0(2i)+x1(5i)+x2(8i)=0,x0(3i)+x1(6i)+x2(9i)=0, x3(i)+x4(4i)+x5(7i)=0,x3(2i)+x4(5i)+x5(8i)=1,x3(3i)+x4(6i)+x5(9i)=0, x6(i)+x7(4i)+x8(7i)=0,x6(2i)+x7(5i)+x8(8i)=0,x6(3i)+x7(6i)+x8(9i)=1 }; f=<{Ainv*A=identity3}; run=<last(mdx=Newton(=<f,=<x),max(normc(f),normc(mdx))); run -> infoLost[ i] 2787964185176708 run -> infoLost[ i] NaN ・初期値を変えてもnormは収束しない clear; A=(i,2i,3i:4i,5i,6i:7i,8i,9i); Ainv=<(x0,x1,x2:x3,x4,x5:x6,x7,x8); x=<{x0,x1,x2,x3,x4,x5,x6,x7,x8}; h=(-i); x_initial=<{h,h,h,h,h,h,h,h,h}; f=<{Ainv*A=identity3}; run=<last(mdx=Newton(=<f,=<x,=<x_initial),max(normc(f),normc(mdx))); run -> infoLost[ i] 23884062379.765785 run -> infoLost[ i] 3.9299189118519258 run -> infoLost[ i] 3.5355470563991256 Ainv*A -> ( infoLost[ i] 1.00262451171875-0.20006942749023438i, infoLost[ i] 0.22774887084960938-0.0094451904296875i, infoLost[ i] -0.547119140625+0.18117904663085938i: infoLost[ i] -0.042938232421875-0.18405914306640625i, infoLost[ i] 0.2579803466796875+0.04792022705078125i, infoLost[ i] 0.55889892578125+0.2799072265625i: infoLost[ i] 0.149261474609375+0.017391204833984375i, infoLost[ i] 0.5675315856933594+0.01317596435546875i, infoLost[ i] 0.9858055114746094+0.008953094482421875i ) |
|
目次
連立 非線形方程式 の解法 |
連立非線形方程式の反復解法について記述する
虚数単位を求めるfull-rank1元2次の方程式を一例に示す x0^2+1=0 ・解を2個示す x0=i; x0^2+1=0 -> -1.2246467991473532e-16i x0=-i; x0^2+1=0 -> 1.2246467991473532e-16i ・非線形方程式を定義する clear; x=<{x0}; f=<{x0^2+1=0}; 初期値を1+2iとした反復6回目の近似解を示す run=<last(mdx=Newton(=<f,=<x,=<{1+2i}),max(normc(f),normc(mdx))); _rn(=<run,,6) -> 4.848187063331881e-11 x -> 6.918085522901255e-17+0.9999999999999997i 初期値を1-2iとした反復6回目の近似解を示す ・上記演算に続けてClear実行しない場合、初期値を直接更新して実行 x0=1-2i; _rn(=<run,,6) -> 4.2544881989018353e-11 x -> -5.067058578678027e-17-1.0000000000000002i ・方程式||関数の次数に応じて収束までの反復回数が増える 実数演算の場合、解が存在しないため、収束しない ・2次の方程式の場合、右辺に移項した関数の極値周辺を右往左往する clear; x=<{x0}; f=<{real(x0)^2+1=0}; || f=<{-(real(x0)^2+1)}; run=<last(mdx=Newton(=<f,=<x,=<{1}),max(normc(f),normc(mdx))); run -> 1.414206491330789 run -> 2500010689.1876636 run -> 625005364.923743 run -> 156251267.10125032 run -> 39062798.523787886 run -> 9765710.483364047 run -> 2441427.7048029117 run -> 610357.137491086 run -> 152589.53659088546 run -> 38147.63324071567 以上の結果をまとめる ・解が複数存在する場合、得られる近似解は初期値に依存する ・解が存在しない場合、解が収束しないか解が無限大に発散する ・高次の方程式||関数の場合、解が存在しても初期値によっては発散する 次に関数を使用したfull-rank2元の連立非線形方程式を一例に示す ・連立非線形方程式と初期値を定義する ・反復6回目の近似解を示す clear; x=<{x0,x1}; x_initial=<{1+i,1-i}; f=<{x0^i-2x1=3i,3x0+exp(x1)=5i}; run=<last(mdx=Newton(=<f,=<x,=<x_initial),max(normc(f),normc(mdx))); _rn(=<run,,6) -> infoLost[ i] 2.2368035825474494e-16 x -> ( infoLost[ i] -0.04901921620544653+2.023423045158351i: 0.07726186556052178-1.434248862158042i ) 同じく引数の列vectorに丸括弧()を使用する場合 ・連立非線形方程式と初期値を定義する ・反復6回目の近似解を示す clear; x=<(x0:x1); x_initial=<(1+i:1-i); f=<(x0^i-2x1=3i:3x0+exp(x1)=5i); run=<last(mdx=Newton(=<f,=<x,=<x_initial),max(normc(f),normc(mdx))); _rn(=<run,,6) -> infoLost[ i] 2.2368035825474494e-16 x -> ( infoLost[ i] -0.04901921620544653+2.023423045158351i: 0.07726186556052178-1.434248862158042i ) 同じく引数の列vectorを直接式渡しする場合 ・mdxのnormを返す式変数runを定義して反復6回目の近似解を示す clear; run=<last( mdx=Newton(=<(x0^i-2x1=3i:3x0+exp(x1)=5i),=<(x0:x1),=<(1+i:1-i)), normc(mdx)); _rn(=<run,,6) -> 2.2368035825474494e-16 {x0,x1} -> ( infoLost[ i] -0.04901921620544653+2.023423045158351i: 0.07726186556052178-1.434248862158042i ) test caseを示す ・strict-modeのsolvex_non_linearを使用 clear; solvex_non_linear(==<f_,=<x_initial_)=<[ out=<x_solved,
init=<last{_ex(=<x,sizer(x_initial_=>),1)},
run=<last{
init=>,run=>,return=out=>,
x_solved=Newton(=<f_,=<x,=<x_initial_,Nmax=20,Nmax,1e-10,1) }, =<return]=>; [f=<{exp(x0)=i},=<solvex_non_linear(=<f,=<{1+i})=>]=>; -> 3.813245622601571e-17+1.5707963267948966i+O(9e-16+1e-15i) exp(ans) -> 6.123233995736766e-17+i+O(1e-15+9e-16i) ・無次元の場合、x=<x0から行列indexを省略可 [f=<{exp(x=>)=i},=<solvex_non_linear(=<f,=<{1+i})=>]=>; -> 3.813245622601571e-17+1.5707963267948966i+O(9e-16+1e-15i) ・Non-strict-modeの場合、式読出し記号=>を省略可 [f=<{exp(x)=i},=<solvex_non_linear(=<f,=<{1+i})=>]=>; -> 3.813245622601571e-17+1.5707963267948966i+O(9e-16+1e-15i) |
|
目次
電気回路 |
電気回路計算について記述する
連立する方程式の列挙基準を示す ・Kirchhoff's Current Law(KCL):接続線を分岐する明示的なnodeのみ(1本線のnodeは解かない) ・Kirchhoff's Voltage Law(KVL):電源優先で独立の閉loop ・状態数(node||loop数)を動的に変更しない 例:SW要素のon/off状態を抵抗値で代替 留意事項を列挙する ・状態を独立可能な場合、各状態の連立方程式を定義して切替える |
|
目次
信号変換 の解法 |
信号変換の解法を列挙する
・高速Fourier変換の解法 ・離散Fourier変換の解法 ・離散Wavelet変換の解法 ・離散Wavelet変換の解法(列代入) |
|
目次
高速 Fourier変換 の解法 |
高速Fourier変換Fast Fourier Transform(FFT)の解法について記述する
前提を列挙する ・信号変換前の領域を実空間と記述する ・信号変換後の領域を波数領域と記述する 実空間 ⇔ 波数領域 ・長さ ⇔ ・波数 ・時間 ⇔ ・周波数 ・信号変換前後のsampling離散点を標本点と記述する ・複素共役をoverlineで記述する Split-Radix-2 FFTを一例に示す(LaTeX形式) ・MathJax表示Checker※CDN通信あり 1次元FFT@Split-Radix-2 実空間 \(x=0,1,...,N_p-1\) における偏角 \(\theta_{x,p}=x2\pi/N_p\) とする標本点 \(f(x)\) に対する1次元FFT@Split-Radix-2 \(N_p=2^p\) \(p=0\) \(F^{N_p=1}_x(u)=f(0)\) \(p\gt0\) \(F_x^{N_p=2^p}(u)\) \(=\sum_{x=0}^{N_p-1}f(x)\mathrm{e}^{-\mathrm{i}u\theta_{x,p}}\) \(=\sum_{x=0}^{N_{p-1}-1}\{f(x)\mathrm{e}^{-\mathrm{i}u\theta_{x,p}}\) \(+f(x+N_{p-1})\mathrm{e}^{-\mathrm{i}u\theta_{x,p}}\mathrm{e}^{-\mathrm{i}u\pi}\}\) \(=\sum_{x=0}^{N_{p-1}-1}\{f(x)\mathrm{e}^{-\mathrm{i}u\theta_{x,p-1}/2}\) \(+f(x+N_{p-1})\mathrm{e}^{-\mathrm{i}u\theta_{x,p-1}/2}\mathrm{e}^{-\mathrm{i}u\pi}\}\) \(=F_x^{N_{p-1}}(u/2)+F_{x+N_{p-1}}^{N_{p-1}}(u/2)\mathrm{e}^{-\mathrm{i}u\pi}\) |
|
目次
離散 Fourier変換 の解法 |
離散Fourier変換Discrete Fourier Transform(DFT)の解法について記述する
前提を列挙する ・1次元の標本点数をNとして順変換DFTと逆変換IDFTの正規化係数(Nf,Ni)の制約条件を示す Nf*Ni=1/N (Nf,Ni)=(1,1/N)のDFT/IDFTを一例に示す(LaTeX形式) ・MathJax表示Checker※CDN通信あり 1次元DFT 実空間 \(x=0,1,...,N-1\) における偏角 \(\theta_x=x2\pi/N\) とする標本点 \(f(x)\) に対する1次元DFT \(F(u)\) \(=\sum_{x=0}^{N-1}f(x)\mathrm{e}^{-\mathrm{i}u\theta_x}\) \(=F_x^N(u)\) 1次元IDFT 波数領域 \(u=0,1,...,N-1\) における偏角 \(\theta_u=u2\pi/N\) とする標本点 \(F(u)\) に対する1次元IDFT \(f(x)\) \(=\frac{1}{N}\sum_{u=0}^{N-1}F(u)\mathrm{e}^{\mathrm{i}x\theta_u}\) \(=\frac{1}{N}\overline{\sum_{u=0}^{N-1}\overline{F(u)}\mathrm{e}^{-\mathrm{i}x\theta_u}}\) \(=f_u^N(x)\) 2次元DFT 実空間 \(x=0,1,...,N-1\) \(y=0,1,...,M-1\) における偏角 \(\theta_x=x2\pi/N\) \(\theta_y=y2\pi/M\) とする標本点 \(f(x,y)\) に対する2次元DFT \(F(u,v)\) \(=\sum_{y=0}^{M-1}\sum_{x=0}^{N-1} f(x,y)\mathrm{e}^{-\mathrm{i}(u\theta_x+v\theta_y)}\) \(=\sum_{y=0}^{M-1}\sum_{x=0}^{N-1} f(x,y)\mathrm{e}^{-\mathrm{i}u\theta_x}\mathrm{e}^{-\mathrm{i}v\theta_y}\) \(=\sum_{y=0}^{M-1}F_x^N(u,y)\mathrm{e}^{-\mathrm{i}v\theta_y}\) \(=F_{xy}^{NM}(u,v)\) 2次元IDFT 波数領域 \(u=0,1,...,N-1\) \(v=0,1,...,M-1\) における偏角 \(\theta_u=u2\pi/N\) \(\theta_v=v2\pi/M\) とする標本点 \(F(u,v)\) に対する2次元IDFT ・Ver.2.69.27以降、一部訂正 \(f(x,y)\) \(=\frac{1}{NM}\sum_{v=0}^{M-1}\sum_{u=0}^{N-1} F(u,v)\mathrm{e}^{\mathrm{i}(x\theta_u+y\theta_v)}\) \(=\frac{1}{NM}\sum_{v=0}^{M-1}\sum_{u=0}^{N-1} F(u,v)\mathrm{e}^{\mathrm{i}x\theta_u}\mathrm{e}^{\mathrm{i}y\theta_v}\) \(=\frac{1}{NM}\sum_{v=0}^{M-1}\sum_{u=0}^{N-1} \overline{F(u,v)}\mathrm{e}^{-\mathrm{i}x\theta_u}\mathrm{e}^{\mathrm{i}y\theta_v}\) \(=\frac{1}{M}\sum_{v=0}^{M-1} \overline{f_u^N(x,v)}\mathrm{e}^{\mathrm{i}y\theta_v}\) \(=\frac{1}{M}\overline{\sum_{v=0}^{M-1} \overline{f_u^N(x,v)}\mathrm{e}^{-\mathrm{i}y\theta_v}}\) \(=f_{uv}^{NM}(x,y)\) test caseを示す(Ver.2.69.27追記) ・1次元の標本点 f={1,2,3,4}; f-> ( 1: 2: 3: 4 ) ・1次元DFT(x)->(u) f={1,2,3,4}; N=sizer(f); Nf=1; Ni=1/N; F=zeros(N,1); F(u)=<{_sx(=<f[x]*e^(-i*u*x*2*pi/N),0,N-1)*Nf}; _su(=<F[u]=F(u)=>,0,N-1); F -> ( 10: -2.0000000000000004+1.9999999999999996i: -2-9.797174393178826e-16i: -1.9999999999999982-2.000000000000001i ) ・1次元IDFT(u)->(x) f(x)=<{_su(=<F[u]*e^(i*x*u*2*pi/N),0,N-1)*Ni}; _sx(=<f[x]=f(x)=>,0,N-1); f -> ( 1.0000000000000004-5.551115123125783e-16i: 2-2.7755575615628914e-16i: 2.9999999999999996-1.1102230246251565e-16i: 4+2.7755575615628914e-16i ) ・2次元の標本点 f={ 1,2,3,4: 5,6,7,8: 9,10,11,12: 13,14,15,16 }; f -> ( 1,5,9,13: 2,6,10,14: 3,7,11,15: 4,8,12,16 ) ・2次元DFT(x,y)->(u,y)->(u,v) f={ 1,2,3,4: 5,6,7,8: 9,10,11,12: 13,14,15,16 }; N=sizer(f); M=sizec(f); Nf=1; Ni=1/N; Mf=1; Mi=1/M; F=zeros(N,M); F(u,v)=<{_sy(=<{_sx(=<f[x][y]*e^(-i*u*x*2*pi/N),0,N-1)*Nf}*e^(-i*v*y*2*pi/M),0,M-1)*Mf}; _sv(=<_su(=<F[u][v]=F(u,v)=>,0,N-1),0,M-1); F -> ( 136, -32.00000000000001+31.999999999999996i, -32-1.4205902870109296e-14i, -31.999999999999975-32.000000000000014i: infoLost[r ] -8.000000000000007+7.999999999999995i, infoLost[r ] 3.1086244689504383e-15-8.881784197001252e-16i, infoLost[r ] 2.6645352591003757e-15+8.881784197001252e-16i, infoLost[r ] 1.1102230246251565e-15+4.218847493575595e-15i: -8-9.797174393178824e-15i, 2.0658177477654226e-15+2.220446049250313e-15i, 2.4492935982947053e-15i, -2.8006058272538343e-15+2.886579864025407e-15i: -7.999999999999982-8.000000000000012i, -4.440892098500626e-16+6.8833827526759706e-15i, -4.440892098500626e-15+4.440892098500626e-15i, -6.8833827526759706e-15-6.661338147750939e-16i ) ・2次元IDFT(x,y)->(u,y)->(u,v)->(x,v)->(x,y) f(x,y)=<{_sv(=<{_su(=<F[u][v]*e^(i*x*u*2*pi/N),0,N-1)*Ni}*e^(i*y*v*2*pi/M),0,M-1)*Mi}; _sy(=<_sx(=<f[x][y]=f(x,y)=>,0,N-1),0,M-1); f -> ( infoLost[ri] 1.0000000000000009-2.220446049250313e-15i, infoLost[ri] 5-2.6645352591003757e-15i, infoLost[ri] 9-2.886579864025407e-15i, infoLost[ri] 13.000000000000002-2.220446049250313e-15i: infoLost[ri] 2.000000000000001-2.220446049250313e-15i, infoLost[ri] 5.999999999999999-1.5543122344752192e-15i, infoLost[ri] 9.999999999999996-1.1102230246251565e-15i, infoLost[ri] 14-1.1102230246251565e-15i: infoLost[ri] 3-2.4424906541753444e-15i, infoLost[ri] 6.999999999999997-4.440892098500626e-16i, infoLost[ri] 10.999999999999996+4.440892098500626e-16i, infoLost[ri] 14.999999999999998+1.5543122344752192e-15i: infoLost[ri] 4-1.9984014443252818e-15i, infoLost[ri] 7.999999999999999+4.440892098500626e-16i, infoLost[ri] 11.999999999999998+1.5543122344752192e-15i, infoLost[ri] 16+3.9968028886505635e-15i ) ・2次元DFT(x,y)->(x,v)->(u,v) F(v,u)=<{_sx(=<{_sy(=<f[x][y]*e^(-i*v*y*2*pi/M),0,M-1)*Mf}*e^(-i*u*x*2*pi/N),0,N-1)*Nf}; _su(=<_sv(=<F[u][v]=F(v,u)=>,0,M-1),0,N-1); F -> ( 136, -32.00000000000001+31.999999999999993i, -32-1.4205902870109296e-14i, -31.99999999999997-32.000000000000014i: infoLost[r ] -8.000000000000004+7.999999999999993i, 5.329070518200751e-15, 1.8357322374478535e-15+1.7763568394002505e-15i, 1.7763568394002505e-15+3.552713678800501e-15i: -8-9.797174393178824e-15i, 1.7763568394002505e-15+1.7763568394002505e-15i, 2.449293598294707e-15i, -1.7763568394002505e-15+3.552713678800501e-15i: -7.999999999999985-8.000000000000014i, 8.881784197001252e-16+5.329070518200751e-15i, -2.9985277160012513e-15+2.6645352591003757e-15i, -3.552713678800501e-15-8.881784197001252e-16i ) ・2次元IDFT(x,y)->(x,v)->(u,v)->(u,y)->(x,y) f(y,x)=<{_su(=<{_sv(=<F[u][v]*e^(i*y*v*2*pi/M),0,M-1)*Mi}*e^(i*x*u*2*pi/N),0,N-1)*Ni}; _sx(=<_sy(=<f[x][y]=f(y,x)=>,0,M-1),0,N-1); f -> ( infoLost[ri] 1.0000000000000029-2.886579864025407e-15i, infoLost[ri] 5.000000000000001-2.7755575615628914e-15i, infoLost[ri] 9-2.3314683517128287e-15i, infoLost[ri] 13.000000000000002-2.55351295663786e-15i: infoLost[ri] 2.0000000000000013-2.1649348980190553e-15i, infoLost[ri] 5.999999999999999-1.3877787807814457e-15i, infoLost[ri] 9.999999999999996-6.661338147750939e-16i, infoLost[ri] 13.999999999999998-3.3306690738754696e-16i: infoLost[ri] 3.000000000000001-1.9984014443252818e-15i, infoLost[ri] 6.999999999999999-7.771561172376096e-16i, infoLost[ri] 10.999999999999998+5.551115123125783e-16i, infoLost[ri] 14.999999999999998+1.7208456881689926e-15i: infoLost[ri] 4.000000000000002-2.3869795029440866e-15i, infoLost[ri] 8-3.3306690738754696e-16i, infoLost[ri] 11.999999999999998+1.6653345369377348e-15i, infoLost[ri] 16+3.1086244689504383e-15i ) |
|
目次
離散 Wavelet変換 の解法 |
離散Wavelet変換Discrete Wavelet Transform(DWT)の解法について記述する
前提を列挙する ・1次元の標本点数をNとして順変換DWTと逆変換IDWTの制約条件を示す N=2^p ・量子化bit数=p ・信号変換の解像度を可逆的にscalingするtwo-scale関係が成立する 多重解像度解析の最も単純なHaar's DWT/IDWTを一例に示す 1次元DWT(x)->(u) ・標本点 1,2,3,4,5,6,7,8 ・two-scale関係式 scaling(t)=scaling(2t)+scaling(2t+1) wavelet(t)=scaling(2t)-scaling(2t+1) ・左右にscaling情報とwavelet情報を分離して再帰的にscaling情報を左側に寄せる 1+2,3+4,5+6,7+8,1-2,3-4,5-6,7-8 1+2+3+4,5+6+7+8,1+2-(3+4),5+6-(7+8),1-2,3-4,5-6,7-8 1+2+3+4+5+6+7+8,1+2+3+4-(5+6+7+8),1+2-(3+4),5+6-(7+8),1-2,3-4,5-6,7-8 ・整理して示す(scaling情報の解像度の降順) 1,2,3,4,5,6,7,8 3,7,11,15,-1,-1,-1,-1 10,26,-4,-4,-1,-1,-1,-1 36,-16,-4,-4,-1,-1,-1,-1 1次元IDWT(u)->(x) ・標本点 36,-16,-4,-4,-1,-1,-1,-1 ・two-scale関係式 scaling(2t)=(scaling(t)+wavelet(t))/2 scaling(2t+1)=(scaling(t)-wavelet(t))/2 ・行vectorの場合 scaling(2t)=0.5*(scaling(t)+wavelet(t)) scaling(2t+1)=0.5*(scaling(t)-wavelet(t)) ・列vectorの場合 scaling(2t)=(scaling(t)+wavelet(t))*0.5 scaling(2t+1)=(scaling(t)-wavelet(t))*0.5 ・scaling情報とwavelet情報から再帰的に元のscaling情報を復元する (36+(-16))/2,(36-(-16))/2,-4,-4,-1,-1,-1,-1 (10+(-4))/2,(10-(-4))/2,(26+(-4))/2,(26-(-4))/2,-1,-1,-1,-1 (3+(-1))/2,(3-(-1))/2,(7+(-1))/2,(7-(-1))/2,(11+(-1))/2,(11-(-1))/2,(15+(-1))/2,(15-(-1))/2 ・整理して示す(scaling情報の解像度の昇順) 36,-16,-4,-4,-1,-1,-1,-1 10,26,-4,-4,-1,-1,-1,-1 3,7,11,15,-1,-1,-1,-1 1,2,3,4,5,6,7,8 2次元DWT/IDWT(x,y)⇔(u,y)⇔(u,v) 1,2,3,4: 5,6,7,8: 9,10,11,12: 13,14,15,16 ⇔ 10,-4,-1,-1: 26,-4,-1,-1: 42,-4,-1,-1: 58,-4,-1,-1 ⇔ 136,-16,-4,-4: -64,0,0,0: -16,0,0,0: -16,0,0,0 2次元DWT/IDWT(x,y)⇔(x,v)⇔(u,v) 1,2,3,4: 5,6,7,8: 9,10,11,12: 13,14,15,16 ⇔ 28,32,36,40: -16,-16,-16,-16: -4,-4,-4,-4: -4,-4,-4,-4 ⇔ 136,-16,-4,-4: -64,0,0,0: -16,0,0,0: -16,0,0,0 test caseを示す ・1次元の標本点 w={1,2,3,4,5,6,7,8}; w-> ( 1: 2: 3: 4: 5: 6: 7: 8 ) ・1次元DWT(x)->(u) w={1,2,3,4,5,6,7,8}; N=sizer(w); W=zeros(N,1); p=round(log2(N)); W(w,N)=<_st(=<last{ a=w[2*t],b=w[2*t+1],W[t]=a+b,W[t+N2]=a-b },N2=N>>1,N2-1); _rn(=<last{W(=<w,first{Np,Np=Np>>1})=>,w=W},Np=1<<p,p); W -> ( 36: -16: -4: -4: -1: -1: -1: -1 ) ・1次元IDWT(u)->(x) w(W,N2)=<_st(=<last{ a=W[t],b=W[t+N2],w[2*t]=0.5*(a+b),w[2*t+1]=0.5*(a-b) },0,N2-1); _rn(=<last{w(=<W,first{Np,Np=Np<<1})=>,W=w},Np=1,p); w -> ( 1: 2: 3: 4: 5: 6: 7: 8 ) ・2次元の標本点 w={ 1,2,3,4: 5,6,7,8: 9,10,11,12: 13,14,15,16 }; w -> ( 1,5,9,13: 2,6,10,14: 3,7,11,15: 4,8,12,16 ) ・2次元DWT(x,y)->(u,y)->(u,v)※N>1 w={ 1,2,3,4: 5,6,7,8: 9,10,11,12: 13,14,15,16 }; N=sizer(w); M=sizec(w); W=zeros(N,M); p=round(log2(N)); q=round(log2(M)); W(w,N)=<_st(=<last{ a=w[2*t],b=w[2*t+1],W[t]=a+b,W[t+N2]=a-b },N2=N>>1,N2-1); _rn(=<last{W(=<w,first{Np,Np=Np>>1})=>,w=W},Np=1<<p,p); W=trans(W); _rn(=<last{w=W,W(=<w,first{Nq,Nq=Nq>>1})=>},Nq=1<<q,q); W=trans(W); W -> ( 136,-64,-16,-16: -16,0,0,0: -4,0,0,0: -4,0,0,0 ) ・2次元IDWT(x,y)->(u,y)->(u,v)->(x,v)->(x,y) w(W,N2)=<_st(=<last{ a=W[t],b=W[t+N2],w[2*t]=0.5*(a+b),w[2*t+1]=0.5*(a-b) },0,N2-1); w=W; _rn(=<last{w(=<W,first{Np,Np=Np<<1})=>,W=w},Np=1,p); w=trans(w); _rn(=<last{W=w,w(=<W,first{Nq,Nq=Nq<<1})=>},Nq=1,q); w=trans(w); w -> ( 1,5,9,13: 2,6,10,14: 3,7,11,15: 4,8,12,16 ) ・2次元DWT(x,y)->(x,v)->(u,v)※M>1 W(w,N)=<_st(=<last{ a=w[2*t],b=w[2*t+1],W[t]=a+b,W[t+N2]=a-b },N2=N>>1,N2-1); w=trans(w); W=trans(W); _rn(=<last{W(=<w,first{Nq,Nq=Nq>>1})=>,w=W},Nq=1<<q,q); W=trans(W); _rn(=<last{w=W,W(=<w,first{Np,Np=Np>>1})=>},Np=1<<p,p); W -> ( 136,-64,-16,-16: -16,0,0,0: -4,0,0,0: -4,0,0,0 ) ・2次元IDWT(x,y)->(x,v)->(u,v)->(u,y)->(x,y) w(W,N2)=<_st(=<last{ a=W[t],b=W[t+N2],w[2*t]=0.5*(a+b),w[2*t+1]=0.5*(a-b) },0,N2-1); w=W; W=trans(W); w=trans(w); _rn(=<last{w(=<W,first{Nq,Nq=Nq<<1})=>,W=w},Nq=1,q); w=trans(w); _rn(=<last{W=w,w(=<W,first{Np,Np=Np<<1})=>},Np=1,p); w -> ( 1,5,9,13: 2,6,10,14: 3,7,11,15: 4,8,12,16 ) |
|
目次
離散 Wavelet変換 の解法 (列代入) |
離散Wavelet変換の解法(列代入)について記述する
Ver.2.76.29以降、行列の列参照と列代入を駆使して2次元DWT/IDWTのalgorithmを整理する ・Ver.2.79.31以降、列参照と列代入の行index=-1 ⇒ Napier数eに演算仕様変更 ・Ver.2.170.41以降、列参照と列代入の[e]を空行列で代替可 Ver.2.747.112以降、列参照と列代入の[e]を廃止 ・2次元の標本点 w={ 1,2,3,4: 5,6,7,8: 9,10,11,12: 13,14,15,16 }; w -> ( 1,5,9,13: 2,6,10,14: 3,7,11,15: 4,8,12,16 ) ・2次元DWT(x,y)->(u,y)->(u,v)※N>1 w={ 1,2,3,4: 5,6,7,8: 9,10,11,12: 13,14,15,16 }; N=sizer(w); M=sizec(w); W=zeros(N,M); p=round(log2(N)); q=round(log2(M)); W_row(w,N)=<_st(=<last{ a=w[2*t],b=w[2*t+1],W[t]=a+b,W[t+N2]=a-b },N2=N>>1,N2-1); W_col(w,N)=<_st(=<last{ a=w[e][2*t],b=w[e][2*t+1],W[e][t]=a+b,W[e][t+N2]=a-b },N2=N>>1,N2-1); _rn(=<last{W_row(=<w,first{Np,Np=Np>>1})=>,w=W},Np=1<<p,p); _rn(=<last{w=W,W_col(=<w,first{Nq,Nq=Nq>>1})=>},Nq=1<<q,q); W -> ( 136,-64,-16,-16: -16,0,0,0: -4,0,0,0: -4,0,0,0 ) ・2次元IDWT(x,y)->(u,y)->(u,v)->(x,v)->(x,y) w_row(W,N2)=<_st(=<last{ a=W[t],b=W[t+N2],w[2*t]=0.5*(a+b),w[2*t+1]=0.5*(a-b) },0,N2-1); w_col(W,N2)=<_st(=<last{ a=W[e][t],b=W[e][t+N2],w[e][2*t]=(a+b)*0.5,w[e][2*t+1]=(a-b)*0.5 },0,N2-1); w=W; _rn(=<last{w_row(=<W,first{Np,Np=Np<<1})=>,W=w},Np=1,p); _rn(=<last{W=w,w_col(=<W,first{Nq,Nq=Nq<<1})=>},Nq=1,q); w -> ( 1,5,9,13: 2,6,10,14: 3,7,11,15: 4,8,12,16 ) ・2次元DWT(x,y)->(x,v)->(u,v)※M>1 W_row(w,N)=<_st(=<last{ a=w[2*t],b=w[2*t+1],W[t]=a+b,W[t+N2]=a-b },N2=N>>1,N2-1); W_col(w,N)=<_st(=<last{ a=w[e][2*t],b=w[e][2*t+1],W[e][t]=a+b,W[e][t+N2]=a-b },N2=N>>1,N2-1); _rn(=<last{W_col(=<w,first{Nq,Nq=Nq>>1})=>,w=W},Nq=1<<q,q); _rn(=<last{w=W,W_row(=<w,first{Np,Np=Np>>1})=>},Np=1<<p,p); W -> ( 136,-64,-16,-16: -16,0,0,0: -4,0,0,0: -4,0,0,0 ) ・2次元IDWT(x,y)->(x,v)->(u,v)->(u,y)->(x,y) w_row(W,N2)=<_st(=<last{ a=W[t],b=W[t+N2],w[2*t]=0.5*(a+b),w[2*t+1]=0.5*(a-b) },0,N2-1); w_col(W,N2)=<_st(=<last{ a=W[e][t],b=W[e][t+N2],w[e][2*t]=(a+b)*0.5,w[e][2*t+1]=(a-b)*0.5 },0,N2-1); w=W; _rn(=<last{w_col(=<W,first{Nq,Nq=Nq<<1})=>,W=w},Nq=1,q); _rn(=<last{W=w,w_row(=<W,first{Np,Np=Np<<1})=>},Np=1,p); w -> ( 1,5,9,13: 2,6,10,14: 3,7,11,15: 4,8,12,16 ) |
|
目次
級数展開 の解法 |
級数展開の解法を列挙する
・Taylor級数・Maclaurin級数の解法 ・Fourier級数の解法 |
|
目次
Taylor・ Maclaurin 級数の解法 |
Taylor級数・Maclaurin級数の解法について記述する
・Computer Algebra System未実装で得られる解は数値解 ・微分高階関数の精度に依存 ・3階微分以降、既定の2次精度では精度不足 Taylor級数・Maclaurin級数 ・0の0乗の定義 0^0 || 0**0 || pow(0,0) -> 1 ・f(x)のx=a周辺のN次打切りTaylor級数TaylorN TaylorN=<_sn(=<{_dx(=<f,n,a)(x-a)^n/n!},0,N); ・f(x)のx=0周辺のN次打切りMaclaurin級数MaclaurinN MaclaurinN=<_sn(=<{_dx(=<f,n,0)x^n/n!},0,N); ・f(x)=exp(x)の場合 f=<exp(x); x=2; f -> 7.38905609893065 ・実数演算の場合 TaylorN=<_sn(=<{_dx(=<f,n,a)(x-a)^n/n!},0,N); MaclaurinN=<_sn(=<{_dx(=<f,n,0)x^n/n!},0,N); f=<exp(x); x=2; a=0; N=3; TaylorN || MaclaurinN -> 6.3333380025161095+O(4e-2) N=5; TaylorN || MaclaurinN -> 7.266696174805806+O(2e+1) N=7; TaylorN || MaclaurinN -> 7.381056210596976+O(2e+2) ・複素数演算の場合 TaylorN=<_sn(=<{_dx(=<f,n,a)(x-a)^n/n!},0,N); f=<exp(x); x=2; a=0; N=3; TaylorN -> 6.333333332137665+0.00000933215700063301i+O(2e-2+2e-2i) N=5; TaylorN -> 7.266666317607307+0.000058921777380024245i+O(4e+0+4e+0i) N=7; TaylorN -> 7.38095752867692+0.00014973248523188646i+O(2e+1+2e+1i) 収束性 ・Taylor級数のN次の項TN TN=<_sn(=<{_dx(=<f,n,a)(x-a)^n/n!},N,N); f=<exp(x); x=2; a=0; N=0; TN -> 1 N=1; TN -> 2.000000000000264+3.199902245182912e-15i+O(2e-12+2e-12i) N=2; TN -> 2.0000000000047273-3.0553419555181785e-12i+O(7e-10+3e-11i) N=3; TN -> 1.3333333321326732+0.000009332160052775064i+O(2e-2+2e-2i) N=4; TN -> 0.6666667002412976+0.000018888944812360706i+O(7e-1+1e-2i) N=5; TN -> 0.26666628522834573+0.00003070067556703053i+O(4e+0+4e+0i) N=6; TN -> 0.0888888278111036+0.000037059768491892605i+O(2e+1+3e-1i) N=7; TN -> 0.025402383258507955+0.00005375093935996962i+O(2e+1+2e+1i) N=8; TN -> 0.006352708017224355+0.00004619914542548148i+O(2e+1+4e-1i) N=9; TN -> 0.0014113419838348632+0.000038423321810908794i+O(5e+0+5e+0i) N=10; TN -> 0.000280289701751799+0.00003279136299319164i+O(1e+0+2e-2i) |
|
目次
Fourier 級数の解法 |
Fourier級数の解法について記述する
・Computer Algebra System未実装で得られる解は数値解 ・積分高階関数の精度に依存 ・既定で4次精度の積分区間の分割数=100 Fourier級数 ・周期関数f(x)のN次打切り複素Fourier級数(部分和) FourierN_sym=<_sn(=<{cn*e^(i(n)x)},-N,N)/*omega=1*/; cn=<_it(=<{ft*e^(-i(n)t)},-pi,pi)/(2pi)/*t=[-pi,pi]*/; ・f(x)=e^(i(2.5)x)の場合 fx=<e^(i(2.5)x); ft=<e^(i(2.5)t); x=2; fx -> 0.28366218546322625-0.9589242746631385i N=1; FourierN_sym -> infoLost[ri] 0.2534807789507349-0.1102612365002427i+O(2e-6+2e-6i) N=3; FourierN_sym -> infoLost[ri] 0.3468103654284403-0.7325756973228494i+O(2e-6+2e-6i) N=5; FourierN_sym -> infoLost[ri] 0.29934712994045387-1.0833440107828247i+O(2e-6+2e-6i) ・複素Fourier多項式FourierN(Ver.2.809.131以降、omega導入のFourierN参照) ・三角波 ft=<asin(sin(t)); ・矩形波 ft=<sign(asin(sin(t))); || ft=<sign(sin(t)); ・のこぎり波 ft=<atan(tan(t)); ・逆のこぎり波 ft=<-atan(tan(t)); |
|
目次
極限の解法 |
極限の解法について記述する
・Computer Algebra System未実装で得られる解は限定的なcaseの数値解 ・L'Hôpitalの定理を使用する場合、微分高階関数の精度に依存 複素数演算の場合、次の極限演算不可 1/0 -> NaN ・0割の演算未定義のため、次の反則が発生 0*Infinity -> NaN 実数演算の場合 1/0 -> Infinity MIN_VALUE -> 5e-324 1/(-MIN_VALUE) -> -Infinity 1/(+MIN_VALUE) -> Infinity 1/Infinity || 1/Inf || 1/pInf -> 0 -Infinity+1 || nInf+1 -> infoLost[r ] -Infinity Infinity-Infinity -> infoLost[r ] NaN 極限値演算のtest caseを列挙する x=MIN_VALUE; x -> 5e-324 sin(x)/x // OK -> 1 sin(-x)/(-x) // OK -> 1 ln(1+x)/x // NG -> infoLost[r ] 0 ・L'Hôpitalの定理 ・複素数演算の場合 _dx(=<{ln(1+x)})/_dx(=<{x}) // OK -> 1.0000000000031541+4.602212346748365e-14i+O(3e-24i) _dx(=<{ln(1-x)})/_dx(=<{-x}) // OK -> 1.0000000000031541+4.602212346748365e-14i+O(2e-16+3e-24i) _dx(=<{ln(1-x)},2)/_dx(=<{-x},2) // NG -> NaN _dx(=<{ln(1-x)},2)/_dx(=<{(-x)^2},2) // OK -> -0.500000000135999+3.0923761182676057e-12i+O(3e-10+1e-11i) ・実数演算の場合 _dx(=<{ln(1+x)})/_dx(=<{x}) // OK -> 0.9999999999991271 _dx(=<{ln(1-x)})/_dx(=<{-x}) // OK -> 0.9999999999991271 _dx(=<{ln(1-x)},2)/_dx(=<{-x},2) // NG -> -Infinity+O(Infinity) _dx(=<{ln(1-x)},2)/_dx(=<{(-x)^2},2) // OK -> -0.4999999999659258+O(3e-10) ・無限大の極限は自明の演算以外は演算不可 y=pInf -> y=Infinity (1/y)/y // OK -> 0 y*y // OK -> Infinity y/(y*y) // NG -> NaN _dy(=<{y})/_dy(=<{y*y}) // NG -> NaN _dy(=<{1/(y*y)})/_dy(=<{1/y}) // NG -> NaN ln(y)/y // NG -> NaN ・有限の場合 y=1e7; y -> 10000000 (1/y)/y -> 1e-14 y*y -> 100000000000000 y/(y*y) -> 1e-7 _dy(=<{y})/_dy(=<{y*y}) -> 5e-8+O(1e+0) _dy(=<{1/(y*y)})/_dy(=<{1/y}) -> 1.9999999999838647e-7-6.386544827326884e-25i+O(1e+0+6e-25i) ln(y)/y -> 0.000001611809565095832 ・収束速さ ln(y)**2/y -> 0.00002597930074134415 ln(y)**3/y -> 0.0004187368542939975 ln(y)**4/y -> 0.006749240670092049 ln(y)**5/y -> 0.10878490669188166 ln(y)**6/y -> 1.7534055314403243 ln(3y)**6/(3y) -> 0.8681193145131064 ln(y*y)**6/(y*y) -> 0.000011221795401218075 ・公式 x=1e7; (1+1/x)**x=e -> 1.3432696333026684e-7 x=1e7; a=1.3; ((x+a)/(x-a))**x=e**(2a) -> -1.9790533656305342e-8 |
|
目次
application |
applicationについて記述する
Painter's pattern||SVG-path||gradation||filter Circuit Simulator's arbitrary non-linear||impedance element ・Arrhenius equationのnon-dimensionalized式変数fの一例 回路要素電流Iに対する未知電圧Vを解く場合 f=<last{I=1,E=0,k=1,I=exp(k*(V-E))-exp(-k*(V-E))} 回路要素電圧Vに対する未知電流Iを解く場合 f=<last{V=1,E=0,k=1,I=exp(k*(V-E))-exp(-k*(V-E))} |
|
目次
独自実装の 反省点 |
基本構文のみで最短かつ確実な実装を選択したため、platform以前に最適化の余地がある
また、すべての結果の確からしさは自己判断のため、致命的な見落としを残す可能性がある 実装の特徴に示す独自実装の反省点を列挙する ・実装上の問題点 ・明示的なcall stackを未実装(debugger・拡張性・保守性・その他) ・scope変数・scope参照(冗長性・その他) ・仕様上の問題点 ・行列前提の仕様(拡張性・その他) ・関数より優先して括弧の中身を自動展開する仕様(arguments実装の複雑化・可読性・その他) ・特殊仕様 ・変数と式変数の区別(useMutex・その他) ・equal記号・代入処理(可読性・その他) ・未最適化(実用性・消費電力・その他) |
|
目次
特有の実装 |
JavaScript特有の実装を列挙する
・namespaceの中に全objectを宣言してglobal searchを省略する(定量的な効果は不明) ・よって関数式のconstructorはhoistingなしの前提で実装する ・既存のframework||plug-inを使用しないが、一部で公式に非推奨の実装を使用する ・instanceのoptionからprototypeの動的な変更(mix-in継承の代替) ・download-linkのonclickでsourceの動的な変更 |
|
目次
実装の特徴 |
実装の特徴を列挙する
・Ver.2.266.62以降、deep-copyの適用対象を最適化(変数・式変数のstore||restore時 ⇒ restore時) ・変数のrestore時、tree構造をdeep-copyで複製して参照上の副作用を単純に回避する ・式変数のrestore時も同様に、入出力のtree構造を複製する ・Ver.2.299.72以降、変数のscopeを動的に確保して解決済みの場合、削除する ・行列演算を含む2項演算子のassociativityは単なるfor-loopで結合順||演算順を保証する ・recursive callを代替する再帰高階関数||再帰callも同様に、独自のcall stackを実装しない ・再帰高階関数||Newton高階行列関数のbreak判定は反復後に実施する ・parserは複数種類の括弧のnestingに対応し、再帰的にtree構造を階層化する ・Ver.2.228.56以降、式渡しも同様に、括弧に変換して階層化する ・以上の階層を変数のscope(useScope||useScopeWith)に活用する ・式変数のargumentsも同様に、最善の仕様を追及していない ・一方、階層毎に区切り文字を先読みすることで短絡評価を再現する ・他方、多用しない前提で直列scope内のscope継承を許容する ・関数を含む実装関数は最善のalgorithmとは限らない(sort関数||spline補間||Gaussの消去法) ・debuggerが存在しないため、変数・式変数はpollution disabledの厳格な制約条件を課す ・よってscope本来の利便性を大きく損なうが、緩和の見通しはない |
|
目次
実装上の 問題点 |
実装上の問題点を列挙する
・高階関数の問題点 |
|
目次
高階関数の 問題点 |
高階関数の問題点を列挙する
・反復処理毎に下記eqn_kのtree構造をdeep-copyで複製するため、 ・高階関数をnestingする場合、致命的にthroughputが低下する(微分の多重化||Lagrange補間) n=4,primes={2,3,5},eqn_k=<last{prime=primes[k],k+1}; _rk(=<eqn_k,N=sizer(primes),N,=<{n%prime==0}); prime -> 2 |
|
目次
仕様上の 問題点 |
仕様上の問題点を列挙する
・代数学準拠の問題点 ・型定義の問題点 ・複素数演算の問題点 ・行列演算の問題点 ・論理演算の問題点 ・未実装の参照共有 ・未実装の参照渡し ・未実装のCAS |
|
目次
代数学準拠の 問題点 |
代数学準拠の問題点を列挙する
・一般的な連立方程式A*x=bの列vector形式で行列関数||高階行列関数を実装したが、 ・ij参照の行列要素が単位tree構造のarr[i][j]参照の場合、 ・x*A=bの行vector形式で実装の方が列方向の欠損要素||転置を意識する負担が少ない (x*A)=(b) ⇔ {trans(A)*trans(x)}={trans(b)} {A*x}={b} ⇔ (trans(x)*trans(A))=(trans(b)) ・また、関数の引数は常に行vectorとして(Gauss_coo行列関数参照) ・内部で入出力の整合性を担保する方が拡張しやすい ・Ver.2.156.38以降、列方向の欠損要素を自動で埋めないため、 ・列vectorの要素数が異なる複数legendのplotに支障がある ・要素数が降順に並ぶ場合、問題ないが、(plot2d_nspline参照) ・昇順に並ぶ場合、列方向の欠損要素をNaNで埋める手順を要する(plot2d()_multi参照) ・以上の余分な手順を省略するため、 ・Ver.2.175.42以降、行vector用のplot2d{xt,yt}を追加する(plot2d{}_multi参照) ・本来、行vector形式に統一して行列関数||plot出力を実装する方が無駄が少ない ・Ver.2.237.56以降、Jacobi高階行列関数||Newton高階行列関数||ODE高階行列関数の第1引数を拡張 列vector形式のみ ⇒ 行||列vector形式を自動判別 ・Ver.2.240.56以降、行列関数の既定形式の仕様変更(列vector形式 ⇒ 行vector形式) 列vector形式の行列関数は削除しない(本来、引数を転置して行vector形式に変換する) |
|
目次
型定義の 問題点 |
型定義の問題点を列挙する
・2次元の行列の型||tree構造を前提とする設計のため、3次元以上の配列は定義不能 ・3次元以上の配列に相当する自由度は変数名symbolで区別する ・3次元以上の配列に相当するfor-loopは展開して記述する 遅延評価で3次元以上の配列を代替する場合、arr_ext参照 |
|
目次
複素数演算の 問題点 |
複素数演算の問題点を列挙する
・演算後にMachine epsilonが残りやすく、整数を意識する負担がある (-1)^0.5 || (-1)**0.5 || pow(-1,0.5) -> 6.123233995736766e-17+i 2^3 || 2**3 || pow(2,3) -> 7.999999999999998 ・同時に、減算||加算で情報落ちが発生しやすく、警告文の判断が難しい (-1)^0.5 || (-1)**0.5 || pow(-1,0.5) -> 6.123233995736766e-17+i ans+1 -> infoLost[r ] 1+i ・実数演算の場合(参考) (-1)^0.5 || (-1)**0.5 || pow(-1,0.5) -> NaN 2^3 || 2**3 || pow(2,3) -> 8 2^3 || 2**3 || pow(2,3) -> 7.999999999999998 ・Ver.2.184.44以降、real自動切替機能を追加 2^3 || 2**3 || pow(2,3) -> 8 round(2^3) -> 8 ・Ver.2.127.34以降、行列sizeの丸め方をfloor ⇒ roundに演算仕様変更 vectorr(2^3) || vectorr(8) // OK -> (0,0,0,0,0,0,0,0) vectorr(round(2^3)) || vectorr(8) // OK -> (0,0,0,0,0,0,0,0) ・整数演算の場合、四則演算子||bit shift演算子を活用する 2*2*2 -> 8 2<<2 || 2*2*2 -> 8 1<<3 || 1*2*2*2 -> 8 8>>>3 || 8>>3 || (((8/2)/2)/2) || 8/(2*2*2) -> 1 |
|
目次
行列演算の 問題点 |
行列演算の問題点を列挙する
・当初、行列積の演算量を多少減らすため、欠損要素を許容したが、 ・Ver.2.76.29以降、行列操作の演算速度を犠牲にする弊害の方が圧倒的に大きい ・よって欠損要素がある場合、error終了の方が実装効率||演算効率が高い 演算効率を優先して行列操作を最適化する場合、内部option参照 |
|
目次
論理演算の 問題点 |
論理演算の問題点を列挙する
x=1; x||(-1) -> 1 x=1; x||(1/0) -> 1 x=0; switch(x,x:1,=<(1/0)) -> NaN x=1; switch(x,x:1,=<(1/0)) -> 1 ・論理演算子の短絡評価を厳密に再現する場合、区切り文字の演算のprecedenceの直後が妥当で ・設計初期段階の仕様変更のため、未対応 before: x=1,y=<((1/0)||2),x||y=> -> (0,0,1) before: x=1,(y=<(1/0))||2,x||y=> -> (0,2,1) LA既定時 after: x=1,y=<((1/0)||2),x||y=> -> (0,0,1) RA選択時 after: x=1,y=<((1/0)||2),x||y=> -> (0,0,2) LA既定時 after: x=1,(y=<(1/0))||2,x||y=> -> (0,2,1) RA選択時 after: x=1,(y=<(1/0))||2,x||y=> -> [MyErr]Invalid REv(y) ・Ver.2.157.38以降、switch高階関数代替の論理演算子(短絡評価)を追加 LA既定時 clear; x=1,y=<(1/0)|||2,x|||y=> -> (0,0,1) RA選択時 clear; x=1,y=<(1/0)|||2,x|||y=> -> (0,0,2) LA既定時 clear; x=1,(y=<(1/0))|||2,x|||y=> -> (0,2,1) RA選択時 clear; x=1,(y=<(1/0))|||2,x|||y=> -> [MyErr]Invalid REv(y) 実装の詳細は内部仕様参照 |
|
目次
未実装の 参照共有 |
参照非共有の項目を列挙する
・変数への代入 ・行列要素pattern matching ・式変数への式代入 ・Ver.2.203.46以降、式変数への式読出し ・Ver.2.234.56以降、reshape行列関数 |
|
目次
未実装の 参照渡し |
・Ver.2.303.73以降、scope変数のscope参照の仕様追加 ・Ver.2.19.6以降、関数のre-name不可 clear; tr=trans -> [MyErr]Invalid FNm(transpose) clear; tr=<trans; tr(1,2:3,4) || (tr=>)(1,2:3,4) -> [MyErr]Invalid FN operation ・Ver.2.19.6以降、高階関数のre-name不可 clear; dx=_dx -> [MyErr]Invalid FNh([object Object]) clear; dx=<_dx; dx(=<{x^2},1,2) -> [MyErr]Invalid FN operation ・式変数の参照共有不可 clear; a=<b+c+d; s=a -> [MyErr]Invalid binary operation clear; a=<b+c+d; s=<a; s -> [MyErr]Invalid binary operation clear; a=<1; a=-1; s=<a; s -> -1 clear; a=<1; a=-1; s=<a=>; s -> 1 clear; a(b,c,d)=<b+c+d; s=a -> [MyErr]Invalid null=> clear; a(b,c,d)=<b+c+d; s=<a; s -> [MyErr]Invalid null=> clear; a(b,c,d)=<b+c+d; s=<a(1,2,3); s -> 6 clear; a(b,c,d)=<b+c+d; s(b,c,d)=<a(b,c,d); s -> [MyErr]Invalid null=> clear; a(b,c,d)=<b+c+d; s(b,c,d)=<a(b,c,d); s(1,2,3) -> 6 clear; a(b,c,d)=<b+c+d; s(b,c,d)=<a(-b,-c,-d); s(1,2,3) -> -6 clear; a(b,c,d)=<b+c+d; s(f,g,h)=<a(-f,-g,-h); s(1,2,3) -> -6 ・定義元argumentsの変数名symbolは独立する clear; a(B)=<{B[0]=B[1],=<B}=>; B=(1,2:3,4); (B,a(=<B)=>,B) -> ( 1,2,3,4,1,2: 3,4,3,4,3,4 ) clear; a(B)=<[B[0]=B[1],=<B]=>; B=(1,2:3,4); (B,a(=<B)=>,B) -> ( 1,2,3,4,1,2: 3,4,3,4,3,4 ) ・値渡し clear; a(b)=<last(b=-1,b); (b=1,a(b)=>,b) -> (0,-1,1) clear; a(b)=<last[b=-1,b]; (b=1,a(b)=>,b) -> (0,-1,1) ・式渡し(参照渡しの代替) clear; a(=<b_)=<last(b=-1,b_=>); (b=1,a(=<b)=>,b) -> [MyErr]Undef eqn(b) clear; a(=<b_)=<last(b=-1,b_=>); (b=1,a(=<{b})=>,b) -> (0,-1,-1) clear; a(=<b_)=<last(b=-1,b_=>); (b=<1,a(=<b)=>,b) -> (0,1,-1) clear; a(=<b_)=<last(b=<-1,b_=>); (b=<1,a(=<b)=>,b) -> (0,1,-1) clear; a(=<b_)=<last[b=<-1,b_=>]; (b=<1,a(=<b)=>,b) -> (0,1,1) |
|
目次
未実装の CAS |
未実装のCAS(Computer Algebra System)について留意事項を列挙する
・applicationのthroughputを優先するため、 ・微分・積分の解析解が得られるcaseも数値誤差を許容する ・よって非線形性が強い関数・級数・極限の演算結果は当てにならない ・陰関数表示のplot出力は非対応 |
|
目次
特殊仕様 |
一般的でない可能性のある仕様を列挙する
・式変数 ・高階関数 ・単項の符号 ・equal記号 ・代入処理 |
|
目次
式変数 |
式変数について記述する
・式変数、式読出し、式渡し、式代入、scope継承の仕様は呼び名含めて一般的でない ・連立方程式をscript入力から解くため、独自に定義している |
|
目次
高階関数 |
高階関数について記述する
・参照透過性の観点から ・関数名に変数名symbolを含む仕様(dummy変数限定)は一般的に許容されない ・特殊仕様関数(関数名に引数の一部を含む仕様)も同様 ・本来、高負荷の正規表現は多用しない ・Ver.2.231.56以降、高階関数||高階行列関数の参照透過性対策を実施 dummy変数の変数名symbol:関数名の一部 ⇒ 関数の引数(Ver.2.812.131以降、旧仕様廃止) ・Ver.2.234.56以降、高階関数||高階行列関数の参照透過性対策を完了 scope変数を参照、上書きする ⇒ scope変数から独立する(引数のみ有効) ・Ver.2.857.158以降、微分高階関数の参照透過性対策を完了 scope変数を参照する ⇒ scope変数から独立する(引数のみ有効) |
|
目次
単項の符号 |
前置単項演算子の符号の仕様を列挙する
・単項の符号は同種の中置2項演算子と区別せず、2項演算子のassociativityに従って演算する ・この時、符号の左側には0が存在すると仮定する LA既定時 +3-5+7-9 || ((((0+3)-5)+7)-9) -> -4 RA選択時 +3-5+7-9 || (0+(3-(5+(7-9)))) -> 0 ・行列も同様に、単項の符号はscalar倍||zeros行列との差||和として扱う -(1,2:3,4) || (-1,:,-1)(1,2:3,4) || (,:,)-(1,2:3,4) -> (-1,-2:-3,-4) +(1,2:3,4) || (+1,:,+1)(1,2:3,4) || (,:,)+(1,2:3,4) -> (1,2:3,4) ・よって実用しないが、符号が連続する場合、RA選択時のみ演算可 LA既定時 --(1,i) || (-)-(1,i) -> [MyErr]Invalid binary operation RA選択時 --(1,i) || (,)-((,)-(1,i)) || (-1)((-1)(1,i)) -> (1,i) LA既定時 ---(1,i) || ((-)-)-(1,i) -> [MyErr]Invalid binary operation RA選択時 ---(1,i) || (,)-((,)-((,)-(1,i))) || (-1)((-1)((-1)(1,i))) -> (-1,-i) |
|
目次
equal記号 |
equal記号=の仕様を列挙する
・代入と判別されないequal記号=は、右辺移項の中置2項演算子として扱う ・2項演算子のassociativityに依存するが、単体使用を前提とする -3=5 || (0-3)=5 || =5+3 -> 8 (1,2:3,4)=(,:,) || =(,:,)-(1,2:3,4) -> (-1,-2:-3,-4) ・Ver.2.88.32以降、定義できない乗算||減算||加算を拡張行列演算に追加 (1,2:3,4)=(,) || =(,)-(1,2:3,4) -> (-1,-2:-3,-4) ・単項の場合、符号同様に左辺には0||zeros行列が存在すると仮定する =8 || 0=8 || =8-0 -> 8 =(1,2:3,4) || (,:,)=(1,2:3,4) || =(1,2:3,4)-(,:,) -> (1,2:3,4) ・本仕様は式変数への方程式の式代入で以下の構文を許容する f=<{x0^2+1=0} || f=<{=-(x0^2+1)} || f=<{-(x0^2+1)} f=<{A*x=b} || f=<{=b-A*x} || f=<{b-A*x} f=<{Ainv*A=identity2} || f=<{=identity2-Ainv*A} || f=<{identity2-Ainv*A} |
|
目次
代入処理 |
行列の代入を伴う演算都合上の仕様を列挙する
・代入を括弧で括った場合、0を返す (x=3) || (3=3) -> 0 ・代入後は0が残ると仮定して演算する(右結合で値を残すNative仕様と異なる) 2(x=3) || 2(3=3) || 2(=3-3) || 2(0) -> 0 (a=(b=1),a,b) -> (0,0,1) ・代入をcomma,||colon:で区切った場合、0を返す max(x=3,-1,-2) || max(0,-1,-2) -> 0 clear; (1,2:3,4:x=5,x) -> (1,2:3,4:0,5) ・ただし、行列を代入しても次元は残らない (x=(1,2:3,4)) -> 0 clear; x=(1,2),x || 0,(1,2) -> (0,1,2) clear; max(x=(-1,-2),min(x)) || max(0,-2) -> 0 vector={1,2,3}:trans(vector)vector -> (0:14) ・行列要素pattern matchingによる代入も同様 (($a,$b)=(1,2)) -> 0 ・式変数への式代入も同様 (x=<(a,b,c,d,e)) -> 0 ・Ver.2.203.46以降、式変数への式読出しも同様 clear; vec(x)=<(x,2*x),vec(1)=>v,v=> -> (0,0,1,2) ・Ver.2.203.46以降、変数への式読出しの仕様廃止 clear; y=<3x-1,x=3,y=>,y=>y0,y0 -> (0,0,8,8,8) |
| 項目 | source抜粋 |
|---|---|
|
目次
前提 |
内部仕様の前提について記述する
任意scriptを実行可能なeval()不使用 Non-use of JavaScript's eval() Calculator用途に特化した実装項目とfile名の対応関係を列挙する ・構文解析・字句解析・単位tree構造 parser.js/operation.js/DATA.js ・変数・関数・区切り文字・演算子のprecedence operation.js ・演算unit operation.js/unit.js ・定義済みの関数・予約語 parser.js/math.js/math_com.js/math_mat.js その他、built-inの関数・演算子を使用 ・連立方程式のsolver solver_com.js |
|
目次
単位tree構造 |
演算単位となる単位tree構造を以下に示す
演算仕様を列挙する ・i行j列の行列要素は2次元配列arr[i][j]を参照する ・無次元の演算の場合、2次元配列の最終要素を参照する Ver.2.73.29以降、定義できない行列演算の拡張機能を追加 Ver.2.74.29以降、拡張行列演算におけるcomma演算子の使用を選択可 ・関数の引数vectorの場合、2次元配列の各行arr[i]を参照する ・演算子のoperandの場合、2次元配列の各要素arr[i][j]を参照する ・行列要素参照用にtag.val同列のobjectを一層追加 Ver.2.249.57以降、const宣言用のflagを追加 Ver.2.261.61以降、const宣言用のdefine判別idを追加 |
|
目次
deep-copy |
tree構造(scope-ids等を含む)のdeep-copyの適用対象を列挙する
・命令文のstatic scopes2d array ・addVar/addEqn最上位関数 ・変数・式変数の ・Ver.2.833.140以降、symbol渡しを自動展開してstore時、式変数のscope継承passの直前 ・高階関数の再帰対象(第1引数) ・Ver.2.408.86以降、Newton高階行列関数の収束計算のretry時、近似解の列vector{x}の初期値 |
|
目次
変数のscope |
scopes2d arrayのstructureを以下に示す
・Ver.2.195.46以降、修正 ・Ver.2.200.46以降、刷新 これに基づく変数のscope仕様について記述する ・n=0にlocal storage object元のreferenceを統合・共通化(命令文を含む) ・循環参照回避のため、scopes2d arrayの要素id=[j,n]でreferenceを代替 ・以降、このreferenceをidsと呼ぶ ・parse段階で階層とscopeの関係に基づくstatic scopes2d arrayを作成 ・同時に対応するidsを単位tree構造のtag.val同列に保存 ・scope付式変数の再利用が存在する場合、scopes2d[最終行]に新規追加 前提を列挙する ・式変数は宣言時の階層に依存する ・定義元のidsをcalled-idsと定義する ・call先のidsをcaller-idsと定義する ・宣言時の階層のreferenceをself-idsと定義する ・上位の階層のreferenceをまとめてupper-idsと定義する ・下位の階層のreferenceをまとめてlower-idsと定義する ・宣言時の階層以上(深さの降順)をself-upper-idsと定義する ・宣言時の階層以下(深さの昇順)をself-lower-idsと定義する ・以下の直列scope内でself-upper-idsの式変数のみcall可 self,[lower,] upper,[self,[lower,]] upper,[upper,[self,[lower,]]] upper,[upper,[self,[lower,[lower,]]]] upper,[upper,[upper,[self,[lower,]]]] upper,[upper,[upper,[upper,[self,]]]] ・ids継承は式変数のself-lower-idsに対して再帰的に継承する 変数のscopeの明示的なids継承が発生する項目を列挙する ・symbolic高階行列関数で式変数の生成時、self-upper-idsを継承 last[x0=1,[x0=2,[x0=3,],_ex(=<x,1,1),x=>]] -> 2 last[x0=1,[[x0=3,],_ex(=<x,1,1),x=>]] -> 1 last[[[x0=3,],_ex(=<x,1,1),x=>]] -> [MyErr]Invalid REv(x0) ・式変数の=<store時、self-upper-idsを継承 clear; [a=2,=<[b=1,a=<first[[b,],b,],=<a=>]=>+a]=> -> 3 ・式変数のscope継承call時、caller-self-upper-idsを継承 Ver.2.32.17以降、scope付式変数の再利用に対応 ・式変数の復帰時、新規idsからself-lower-idsを更新 Ver.2.32.17以降、式変数のargumentsを追加 ・式変数のcall時、式変数のargumentsにcalled-self-upper-idsを継承 式変数のscope継承callについて記述する ・called||caller-self-upper-idsの重複idsをpopで取り出した後、caller-self-upper-idsを継承 ・よってidsはn=0の0階層から取り出すFIFO-queueとする |
|
目次
式変数の arguments |
式変数のargumentsについて記述する
・式変数のcall毎にscopeは動的に作らない(new演算子は未実装) ・parse段階で割当てた定義元のstatic scopes2d arrayを共有する ・以降、argumentsの変数名symbolをargと呼ぶ ・式変数のstore時、argを単位tree構造のtag.val同列に保存 ・argのみ、高階関数のdummy変数同様に、buffer経由でcall前後のscopeが独立する Ver.2.194.45以降、以上の要件から再帰callに対応 ・call先のargument判別の条件分岐が複雑化し、非常に重い 判別対象:記号=<の有無||遅延評価の明示 Ver.2.266.62以降、deep-copyの適用対象を最適化(2重cloneの無駄あり ⇒ なし) |
|
目次
式渡し |
式渡しの仕様は括弧優先の高階関数の実装において必須
・引数が値渡しの場合、関数call前に引数の演算を実行するが、 ・引数が式渡しの場合、関数callまで引数の演算を実行しない ・式渡しと式代入記号=<が共通で遅延評価を保証するため、左結合とする 括弧の中身を自動展開(行列を想定)するため、遅延評価の記号を追加(逆の場合、展開記号を追加) 実装の経緯 ・当初、括弧より関数優先で本仕様はなかったが、括弧優先で再実装時、記号=<を明示 ・さらに、直接式読出し||無名callに流用 ・Ver.2.228.56以降、parse段階でuseScopeWith||scope継承のflagを含む括弧に変換(SEe⇒BTe) ・parse段階でstatic scopes2d arrayのidsを追加 ・operation段階で式代入時、式変数のargumentsのargを追加 ・operation段階で式読出し時、丸括弧()に変換(BTe⇒BT1) |
|
目次
内部option |
console-CLI実行で必要な内部optionの設定項目について記述する
全objectはglobal scopeから見えないMy_entryで始まる My_entry.parserに渡すdata objectを次に示す var data = {trees:null, options:{}, vars:{}, eqns:{}}; 内部optionに相当するdata.optionsのpropertyを以下に列挙する ・Ver.2.76.30以降、makeLogの内部optionが反映されない不具合を修正 ・Ver.2.76.30以降、expDigitの仕様追記(内部optionは無効) ・makeLog: 演算終了後にlog出力用の文字列を作成するflag makeLog=true設定で整形なしのlogを作成 makeLog=2設定で行列を整形表示するlogを作成 console-CLI実行でlogを作る場合、flagを立てる 一例を次に示す(以降のflagも同様) ・useComplex: 複素数を使用するflag ・useMatrix: 行列を使用するflag 以降、省略で既定値 ・useStrict: strict-modeを使用するflag ・useScope: 変数のscopeを使用するflag ・useStaticScopes2dArray: Ver.2.299.72以降、static scopes2d arrayを共有するflag ・useScopeWith: Ver.2.213.47以降、式代入記号=<に変数のscopeを使用するflag ・useFunc: Ver.2.221.50以降、実装関数名の大文字・小文字のformatを選択するflag ・use$let: Ver.2.249.57以降、再代入と重複宣言を禁止するconst宣言の既定値を選択するflag ・useMutex: Ver.2.250.57以降、変数・式変数の同一変数名symbolの宣言禁止を選択するflag ・isRightAssociativityBR: 2項演算子のassociativityをRA選択に変更するflag ・isDIVprior2OMUL: 記号省略乗算より除算を優先するflag ・expDigit: 演算結果を表示する指数表記の桁数(内部optionは無効) ・checkError: 情報落ちの発生や微分・積分の数値誤差を評価するflag ・checkComplex: Ver.2.151.38||2.163.39以降、虚部の-0||NaNをlog表示するflag ・precedence: comma,区切りで演算子のtag名を列挙した文字列 ・matSizeMax: 行列size指定の行||列のlengthの上限値= ・depthMax: Ver.2.144.36以降、operation段階のnesting深さの上限値=300 ・useRetry: Ver.2.408.86以降、収束計算のretry機能を使用するflag ・isRelative_epsN: epsNを相対誤差に変換するflag ・epsN: Newton法の絶対誤差の収束判定実数値 ・dxJ: Jacobi行列演算時の1階偏微分の差分刻み実数値 ・dxD: 有限差分による1階微分の差分刻み実数値 ・orderD: 有限差分による微分の精度次数 ・orderT: 有限差分による常微分の精度次数 ・NI: 有限差分による積分区間の分割数 ・orderI: 有限差分による積分の精度次数 以降、console-CLI実行は無効 ・useWorker: Workerを使用するflag ・oldPlot2d: Ver.2.33.17以前のplot2d 0.seriesを使用するflag ・test: Ver.2.207.46以降、calc-configにuseScope||precedenceを追加表示するflag browser-GUI実行の場合、URLのGET入力でUI設定値||既定値を上書き可 |
|
目次
独自eval |
console-CLI実行用の独自evalについて記述する
独自evalは次のstatic methodでconsoleからcallする ・演算内容の文字列を引数に渡すと演算結果の文字列が返る My_entry.eval("2*3") -> "6" 内部optionは以下の既定値 ・Ver.2.184.44以降、real自動切替の内部option既定値に変更 test caseを列挙する |
|
目次
変数・関数・ 区切り文字・ 演算子の precedence |
変数・関数・区切り文字・演算子のprecedenceについて記述する
・Ver.2.167.40以降、厳密等価演算子を追加 ・Ver.2.168.41以降、論理XOR演算子を追加 ・Ver.2.192.44以降、dot演算子を追加(URi,URfをURに統合) ・Ver.2.196.46以降、条件演算子代替のANDss||ORss演算子を追加 ・Ver.2.213.47以降、useScopeWithを追加(BTe) ・Ver.2.225.52以降、厳密不等価演算子を追加 ・Ver.2.228.56以降、SEeを削除 ・Ver.2.298.72以降、変数のprototype method代替のmethod演算子を追加(REv) ・Ver.2.752.113以降、前置単項演算子(PU)のsize演算子を追加 ・Ver.2.847.153以降、行列の厳密等価||不等価演算子を追加(BRrl) 配列要素の定義順で演算のprecedenceを動的に変更可能とする operation.js抜粋 |
|
目次
定義済みの 関数・予約語 |
定義済みの関数・予約語について記述する
・Ver.2.154.38以降、rad2deg/deg2rad/cdot関数を追加 ・Ver.2.158.38以降、NaN||論理値literalを追加 ・Ver.2.159.38以降、isNaN関数を追加 ・Ver.2.165.39以降、reserved tokenを追加 ・Ver.2.167.40以降、seq||sne関数を追加 ・Ver.2.167.40以降、bit演算子と論理演算子の演算子代替関数を追加 ・Ver.2.168.41以降、複素数の演算子代替関数を追加 ・Ver.2.172.42以降、isFalse/isTrue行列関数を追加 ・Ver.2.176.43以降、補間関数を追加 ・Ver.2.183.44以降、space初期化行列関数を追加 ・Ver.2.186.44以降、camin/camax関数を追加 ・Ver.2.187.44以降、normr/norm/normc行列関数を追加 ・Ver.2.230.56以降、下記switch文を関数化 ・Ver.2.234.56以降、reshaper/reshape/reshapec行列関数を追加 ・Ver.2.243.56以降、hasVs/hasEs最上位関数を追加 ・Ver.2.268.62以降、最上位関数のvar||eqnを統合 ・Ver.2.301.72以降、escape記号を追加 ・Ver.2.303.73以降、scope参照の仕様追加(参照渡し記号?を予約) ・Ver.2.321.77以降、fft1d/ifft1d関数@radix=2を追加(高速フーリエ変換のprogram例を参考) 予約語は大文字・小文字・全角・半角を区別しない ・Ver.2.170.42以降、追加項目 ・Ver.2.221.50以降、実装関数名の大文字・小文字のformatを選択するuseFuncを追加 Ver.2.390.86以降、useFuncの内部wrapper関数を追加 ・Ver.2.390.86以降、命令文とmethod演算子以外の全予約語に対応(定数・虚数単位iを含む) ・Ver.2.766.116以降、nand/xnor/nor/cnand/cxnor/cnor関数を追加 ・Ver.2.825.139以降、reshapez行列関数を追加 parser.js抜粋 予約記号の正規表現は正規表現text置換参照 |
|
目次
NaN対応結果 |
定義済みの関数のNaN対応結果を以下に示す
・comment文:// 対応後の演算結果 ・Ver.2.170.42以降、追加項目 |
|
目次
接頭辞の 正規表現 |
接頭辞を判定する正規表現について記述する
Ver.2.146.37以降、正規表現を修正 0(?:[xXbBoO][0-9a-zA-Z]+) ・厳密な正規表現は使用しない ・記号省略乗算を許容した弊害への対策 接頭辞判定の正規表現は正規表現text置換参照 |
|
目次
log関数 |
複素数演算のlog関数について記述する
Ver.2.149.38以降、複素対数関数の性質を見直して内部仕様を修正 ・引数の実部が負の場合、(2*pi)iの数値誤差が生じやすい不具合を対策 ・誤解を招く数値誤差を解消 ln(1/(-1)) || ln(1/(1-2)) -> 3.141592653589793i ln(1/(-2)) -> -0.6931471805599453+3.141592653589793i ln(-1) -> 3.141592653589793i ln(-0.5) -> -0.6931471805599453+3.141592653589793i ・Ver.2.184.44以降、auto-real selected時 ln(-1) -> NaN ln(-0.5) -> NaN ・log関数からcallする偏角算出のatan2関数を修正 Math.atan2(y || 0, x || 0) |
|
目次
atan2関数 |
実数演算のatan2関数について記述する
built-inのatan2関数の挙動 Math.atan2(-0, -1) -> -3.141592653589793 Math.atan2(0, -1) -> 3.141592653589793 Math.atan2(-0 || 0, -1) -> 3.141592653589793 Math.atan2(0, -0) -> 3.141592653589793 Math.atan2(-0, -0) -> -3.141592653589793 Math.atan2(0, 0) -> 0 Math.atan2(-0, 0) -> -0 Math.atan2(-0, 1) -> 0 atan2関数の挙動 atan2(-0,-1) -> -3.141592653589793+O(6e+0) atan2(0,-1) -> 3.141592653589793 atan2(-0||0, -1) -> 3.141592653589793 atan2(0,-0) -> 3.141592653589793+O(3e+0) atan2(-0,-0) -> -3.141592653589793+O(3e+0) atan2(0,0) -> 0 ・Ver.2.151.38以降、実部の-0表示に対応 atan2(-0,0) -> -0 atan2(-0,1) -> 0 |
|
目次
NaN対応 |
NaN対応について記述する
Ver.2.170.42以降、実装関数の引数がNaNの場合、発生する不具合を一括修正 ・未定義の返値を返す関数を修正 ・引数不足の場合、予期せぬerror終了が発生する一部の関数を修正 修正前の不具合を列挙する identity(NaN) -> Invalid array length gcd(1,NaN) -> Maximum call stack size exceeded argument(NaN) -> 0 Kdelta(NaN) -> 0 combin(NaN,1) || permut(NaN,1) -> 1 combin(1,NaN) || permut(1,NaN) -> 0 NaN! || fact(NaN) -> 1 mat2coo(NaN) || mat2coo(0) -> (:: ) or(NaN) || or(0) // NaN||undefined -> undefined ・別途、引数不定の関数の不具合 camin(NaN) -> NaN camin(i) -> i 修正後の対策を列挙する ・isNaN判定を追加 identity(NaN) -> [MyErr]Invalid matrix size gcd(1,NaN) -> NaN argument(NaN) -> NaN Kdelta(NaN) -> NaN combin(NaN,1) || permut(NaN,1) -> NaN combin(1,NaN) || permut(1,NaN) -> NaN NaN! || fact(NaN) -> NaN ・未定義の場合、 mat2coo(NaN) || mat2coo(0) -> (NaN:NaN:NaN) ・引数不足の場合、NaNを返す or(NaN) || or(0) -> NaN ・引数不定の関数の場合、同じ引数を追加して正常化 camin(NaN) || camin(NaN,NaN) -> NaN camin(i) || camin(i,i) -> 1 結果の一覧はNaN対応結果参照 |
|
目次
-0表示対応 |
log表示の-0表示対応について記述する
Ver.2.151.38以降、実部の-0表示に対応 ・toLocaleString()を使用 -0 -> -0 (-0) -> -0 (-0,-0) -> (-0,-0) x=(-0),x -> (0,-0) ・指数表記選択の場合 -0 -> 0e+0 -0のNative仕様 -0 -> -0 (-0) -> -0 -0 * 0 -> -0 -0 * 1 -> -0 -0 * (-1) -> 0 -0 + 0 || 0 + (-0) -> 0 演算結果のlog表示 ・csv-formatで-0を入力 -0 -> -0 (-0) -> -0 ・無次元の演算の場合、互換性あり (-0)*0 -> -0 (-0)*1 -> -0 (-0)*(-1) -> 0 (-0)+0 || 0+(-0) -> 0 ・有次元の演算の場合、互換性なし (-0)*0 -> 0 (-0)*1 -> 0 (-0)*(-1) -> 0 (-0)+0 || 0+(-0) -> 0 虚部の-0をlog表示する場合、内部option参照 cos(pi/4) -> 0.7071067811865476-0i |
|
目次
短絡評価 |
短絡評価の実装について記述する
Ver.2.157.38以降、switch高階関数代替の論理演算子(短絡評価)を追加 ・Ver.2.196.46以降、条件演算子代替の論理演算子(literal)を追加 operand判定時、構文規則の先読み対策(operandを全走査する仕様の対策)を列挙する ・代入記号=||=<を区切り文字として追加で判定 式変数への式代入直後の演算のprecedenceで変数への代入より優先する ・論理ANDsと論理ORsの優先順位は次の判定で区別(論理ANDs優先の挙動) 論理ANDsの判定時、別の論理ANDs||論理ORsを区切り文字として追加で判定 |
| 式変数名 | algorithm |
|---|---|
|
目次
template |
clear;
template(x,y,=<symbol_eqn_,=<eqn_,==<symbol__eqn__,==<eqn__)=<[ out=<[=<(symbol_eqn_=>,eqn_=>,symbol__eqn__=>,eqn__=>)]=>, scope2storage=<last{0},
init=<last{0},
run=<last{0},
init=>,run=>,return=out=>,scope2storage=>,
=<return]=>; [x=1,y=2,f=3,f=<{x,y},=<template(x,f/*var||eqn*/,=<f,=<{x,y},=<f,=<{x,y})=>]=>; [x=1,y=2,f=3,f=<(x:y),=<template(x,last(f),=<f,=<(x:y),=<f,=<(x:y))=>]=>; [x=1,y=2,f=3,f=<[x:y],=<template(x,last(f),=<f,=<[x:y],=<f,=<[x:y])=>]=>; [x=1,y=2,f=3,f=<(x:y),=<template(x,=<last(f),=<f,=<(x:y),=<f,=<(x:y))=>]=>; [x=1,y=2,f=3,f=<[x:y],=<template(x,=<last(f),=<f,=<[x:y],=<f,=<[x:y])=>]=>; [x=1,y=2,f=3,f=<(x:y),=<template(x,=<last(f=>),=<f,=<(x:y),=<f,=<(x:y))=>]=>; [x=1,y=2,f=3,f=<[x:y],=<template(x,=<last(f=>),=<f,=<[x:y],=<f,=<[x:y])=>]=>; clear; [f(=<A)=<A=>+B,B=-1,C=-2,g=<B, [B=10,C=11,g=<C,h=<g=>+B,[B=20,f(=<h)=>,f(==<h)=>,f(=<h)==>,f(==<h)==>]]]: f(=<A)=<A=>+B,B=-1,C=-2,g=<B, [B=10,C=11,g=<C,h=<g=>+B,[B=20,f(=<h)=>,f(==<h)=>,f(=<h)==>,f(==<h)==>]]: f(==<A)=<A=>+B,B=-1,C=-2,g=<B, [B=10,C=11,g=<C,h=<g=>+B,[B=20,f(=<h)=>,f(==<h)=>,f(=<h)==>,f(==<h)==>]]: f(=<A)=<A==>+B,B=-1,C=-2,g=<B, [B=10,C=11,g=<C,h=<g=>+B,[B=20,f(=<h)=>,f(==<h)=>,f(=<h)==>,f(==<h)==>]]; clear; B=-1,g=<B/*here*/,[B=10,[B=20,[B=30,f=<g=/*required*/>,=<f]=>f,=<f]=>f,=<f]=>f,f=>,f==>: B=-1,g=<B,[B=10,[B=20,[B=30,f=<g==>,=<f]=>f,=<f]=>f,=<f]=>f,f=>,f==>: B=-1,g=<B,[B=10,[B=20,[B=30,f=/*disabled*/=<g=>,=<f]=>f,=<f]=>f,=<f]=>f,f=>,f==>: B=-1,g=<B,[B=10,[B=20,[B=30,f=/*disabled*/=<g==>,=<f]=>f,=<f]=>f,=<f]=>f,f=>,f==>: B=-1,[B=10,[B=20,g=<B,[B=30,g=>f/*resolved*/,=<f]=>f,=<f]=>f,=<f]=>f,f=>,f==>: B=-1,[B=10,[B=20,g=<B,[B=30,g==>f/*resolved*/,=<f]=>f,=<f]=>f,=<f]=>f,f=>,f==>: B=-1,[B=10,[B=20,g=<B,[B=30,[=<g]=>f,=<f]=>f,=<f]=>f,=<f]=>f,f=>,f==>: B=-1,[B=10,[B=20,g=<B,[B=30,[=<=<g]=>f,=<f]=>f,=<f]=>f,=<f]=>f,f=>,f==>: B=-1,[B=10,[B=20,g=<B,[B=30,[==<g]=>f,=<f]=>f,=<f]=>f,=<f]=>f,f=>,f==>: B=-1,[B=10,[B=20,g=<B,[B=30,[==<=<g]=>f,=<f]=>f,=<f]=>f,=<f]=>f,f=>,f==>: B=-1,[B=10,[B=20,g=<B,[B=30,[=<==<g]=>f,=<f]=>f,=<f]=>f,=<f]=>f,f=>,f==>: B=-1,[B=10,[B=20,g=<B,[B=30,[=<g]==>f,=<f]=>f,=<f]=>f,=<f]=>f,f=>,f==>: B=-1,[B=10,[B=20,g=<B,[B=30,[==<g]==>f,=<f]=>f,=<f]=>f,=<f]=>f,f=>,f==>: B=-1,[B=10,g=<B,[B=20,[B=30,=<g]=>f,=<f]=>f,=<f]=>f,f=>,f==>: B=-1,[B=10,[B=20,g=<B,[B=30,=<g]=>f,=<f]=>f,=<f]=>f,f=>,f==>: B=-1,[B=10,[B=20,g=<B,[B=30,==<g]=>f,=<f]=>f,=<f]=>f,f=>,f==>: B=-1,[B=10,[B=20,g=<B,[B=30,==<=<g]=>f,=<f]=>f,=<f]=>f,f=>,f==>: B=-1,[B=10,[B=20,g=<B,[B=30,=<==<g]=>f,=<f]=>f,=<f]=>f,f=>,f==>: B=-1,[B=10,[B=20,g=<B,[B=30,=<=<g]==>f,=<f]=>f,=<f]=>f,f=>,f==>: B=-1,[B=10,[B=20,g=<B,[B=30,=<=<g]=>f,==<f]=>f,=<f]=>f,f=>,f==>: B=-1,[B=10,[B=20,g=<B,[B=30,=<=<g]=>f,=<==<f]=>f,=<f]=>f,f=>,f==>: B=-1,[B=10,[B=20,g=<B,[B=30,=<=<g]=>f,=<f]==>f,=<f]=>f,f=>,f==>: B=-1,[B=10,[B=20,g=<B,[B=30,=<=<g]=>f,=<f]=>f,==<f]=>f,f=>,f==>: B=-1,[B=10,[B=20,g=<B,[B=30,=<=<g]=>f,=<f]=>f,=<==<f]=>f,f=>,f==>: B=-1,[B=10,[B=20,g=<B,[B=30,=<=<g]=>f,=<f]=>f,=<f]==>f,f=>,f==>: B=-1,[B=10,[B=20,g=<B,[B=30,==<==<g]=>f,=<f]=>f,=<f]==>f,f=>,f==>: B=-1,[B=10,[B=20,[B=30,==<=<B]=>f,=<f]=>f,=<f]=>f,f=>,f==>: B=-1,[B=10,[B=20,[B=30,=<=<B]==>f,=<f]=>f,=<f]=>f,f=>,f==>: B=-1,[B=10,[B=20,[B=30,=<=<B]=>f,==<f]=>f,=<f]=>f,f=>,f==>: B=-1,[B=10,[B=20,[B=30,=<=<B]=>f,=<f]==>f,=<f]=>f,f=>,f==>: B=-1,[B=10,[B=20,[B=30,=<=<B]=>f,=<f]=>f,==<f]=>f,f=>,f==>: B=-1,[B=10,[B=20,[B=30,=<=<B]=>f,=<f]=>f,=<f]==>f,f=>,f==>: B=-1,[B=10,[B=20,[B=30,=<B/*resolved*/]=>f,=<f]=>f,=<f]==>f,f=>,f==>/*Ver.2.830.140~*/; clear; B=-1,[B=10,=<[B=20,g=<B,=<[B=30,=<g/*not-resolved*/]=>]=>]=>g,g=>,g==>: B=-1,[B=10,=<[B=20,g=<B,=<[B=30,==<g]=>]=>]=>g,g=>,g==>: B=-1,[B=10,=<[B=20,g=<B,g=-B,=<[B=30,=<g/*var*/]=>]=>]=>: //B=-1,[B=10,=<[B=20,g=<B,=<[B=30,=<g/*not-resolved*/]=>]=>]=> B=-1,[B=10,=<[B=20,g=<B,=<[B=30,=<g=>]=>]=>]=>: B=-1,[B=10,=<[B=20,g=<B,=<[B=30,=<g==>]=>]=>]=>: B=-1,[B=10,=<[B=20,g=<B,=<[B=30,=/*disabled*/=<g=>]=>]=>]=>: B=-1,[B=10,=<[B=20,g=<B,=<[B=30,=/*disabled*/=<g==>]=>]=>]=>; clear; a0=-1; call_f(a0)=<(a=a0,f(3)=>,f(3)==>); make_f(a)=<[g(x)=<a*x,=<g]=>f,make_f(a0)=>,call_f(1)=>,call_f(2)=>: make_f(a0)=<[a=a0,g(x)=<a*x,=<g]=>f,make_f(a0)=>,call_f(1)=>,call_f(2)=>: make_f(a)=<[g(x)=<a*x,=<g]=>,make_f(a0)=>f,call_f(1)=>,call_f(2)=>: ,make_f(a0)==>f,call_f(1)=>,call_f(2)=>: make_f(a0)=<[a=a0,g(x)=<a*x,=<g]=>,make_f(a0)=>f,call_f(1)=>,call_f(2)=>: ,make_f(a0)==>f,call_f(1)=>,call_f(2)=>; |
|
目次
scope_NG |
命令文||scope付式変数の再利用参照
clear; scope_NG1(x)=<[x=x,x,last[x=x/*NG*/,x],x]; scope_NG2(x)=<2*[x=x,x,last[x=x/*NG*/,x],x]; scope_NG3(x)=<last[,3]*[x=x,x,last[x=x/*NG*/,x],x]; scope_NG4(x)=<last[x=4,x]*[x=x/*NG*/,x,last[x=x/*NG*/,x],x]; check_all(x)=<(scope_NG1(x)=>:scope_NG2(x)=>:scope_NG3(x)=>:scope_NG4(x)=>); store; scope_NG1(1)=>:scope_NG1(-1)=>; scope_NG2(1)=>:scope_NG2(-1)=>; scope_NG3(1)=>:scope_NG3(-1)=>; scope_NG4(1)=>:scope_NG4(-1)=>; restore; check_all(1)=>; check_all(-1)=>; restore; check_all(1)=>; restore; check_all(-1)=>; |
|
目次
short_ circuit |
論理演算子(短絡評価)||論理演算子(literal)||switch高階関数参照
clear; sw_var_NG1(sw)=<[x=0,sw&&&x=1||||x=-1,=<x]=>,sw_var_NG1(false)=>,sw_var_NG1(true)=>; sw_var_NG2(sw)=<[x=0,sw&&&(x=1)|||(x=-1),=<x]=>,sw_var_NG2(false)=>,sw_var_NG2(true)=>; sw_var_NG3(sw)=<[x=0,sw&&(x=1)||(x=-1),=<x]=>,sw_var_NG3(false)=>,sw_var_NG3(true)=>; sw_var_OK1(sw)=<[x=0,sw&&&(x=1)||||(x=-1),=<x]=>,sw_var_OK1(false)=>,sw_var_OK1(true)=>; sw_var_OK2(sw)=<[x=0,sw&&&(,x=1)|||(,x=-1),=<x]=>,sw_var_OK2(false)=>,sw_var_OK2(true)=>; sw_var_OK3(sw)=<[x=0,switch(sw,=<x=1:1,=<x=-1),=<x]=>,sw_var_OK3(false)=>,sw_var_OK3(true)=>; sw_eqn_NG1(sw)=<[sw&&&f=<1||||f=<-1,=<f=>]=>,sw_eqn_NG1(false)=>,sw_eqn_NG1(true)=>; sw_eqn_NG2(sw)=<[sw&&&(f=<1)|||(f=<-1),=<f=>]=>,sw_eqn_NG2(false)=>,sw_eqn_NG2(true)=>; sw_eqn_NG3(sw)=<[sw&&(f=<1)||(f=<-1),=<f=>]=>,sw_eqn_NG3(false)=>,sw_eqn_NG3(true)=>; sw_eqn_OK1(sw)=<[sw&&&(f=<1)||||(f=<-1),=<f=>]=>,sw_eqn_OK1(false)=>,sw_eqn_OK1(true)=>; sw_eqn_OK2(sw)=<[sw&&&(,f=<1)|||(,f=<-1),=<f=>]=>,sw_eqn_OK2(false)=>,sw_eqn_OK2(true)=>; sw_eqn_OK3(sw)=<[switch(sw,=<f=<1:1,=<f=<-1),=<f=>]=>,sw_eqn_OK3(false)=>,sw_eqn_OK3(true)=>; |
|
目次
matching |
行列要素pattern matching参照
clear; [ a=1,($a,$b)=(-1,a),(a,b): a=1,($a,a)=(-1,$b),(a,b): a=1,(-1,$b)=($a,a),(a,b): a=1,(-1,a)=($a,$b),(a,b) ]; clear; switch_NG4lazy=<[ A=(1,2:3,4), ($A[0],$A[1])=(=<A[1],=<A[0]), ($A[][0],$A[][1])=(=<A[][1],=<A[][0]), =<(false:A)]=>; switch_OK=<[ A=(1,2:3,4), B=A, ($A[0],$A[1])=(=<B[1],=<B[0]), B=A, ($A[][0],$A[][1])=(=<B[][1],=<B[][0]), =<(true:A)]=>; switch_NG4lazy=>:switch_OK=>; |
|
目次
list |
行列結合参照(method演算子非対応)
clear; N=6; make_f(a)=<[aa=a*a,=<(x)=<aa*x]=>; list_f=_r((arr)=<(arr:make_f(__n__)=>),=<[],N); _r((arr)=<(arr,{(list_f[__n__-1])(1)=>,(list_f[__n__-1])(2)=>,(list_f[__n__-1])(3)=>}),=<[],N); |
|
目次
scope 2storage |
行列要素pattern matching||式変数への式読出し||無名call参照
clear; t0=(1,2,3:4,5,6); xt=<false; yt=<false; call_xy_var0(=<xy)=<{=<xy[0]=>,=<xy[1]=>}; call_xy_var1(=<xy)=<{=<(xy=>)[0]=>,=<(xy=>)[1]=>}; call_xy_eqn0(=<xy)=<{=<(xy[0]=>)=>,=<(xy[1]=>)=>}; call_xy_eqn1(=<xy)=<{=<((xy=>)[0]=>)=>,=<((xy=>)[1]=>)=>}; var2var=<[xt=t0,yt=(t0)i,out_lazy=<{=<xt,=<yt},=<out_lazy]=>; eqn2var=<[xt=<t0*2,yt=<(t0*2)i,out_lazy=<{=<xt,=<yt},=<out_lazy]=>; undefined2var=<[out_lazy=<{=<xt,=<yt},=<out_lazy]=>; var2var=>xy_var; store; {$xt,$yt}=call_xy_var0(=<xy_var)=>/*Ver.2.269.62~*/; {xt,yt}; restore; {$xt,$yt}=call_xy_var1(=<xy_var)=>/*Ver.2.269.62~*/; {xt,yt}; restore; eqn2var=>xy_eqn; store; {$xt,$yt}=call_xy_eqn0(=<xy_eqn)=>/*Ver.2.269.62~*/; {xt,yt}; restore; {$xt,$yt}=call_xy_eqn1(=<xy_eqn)=>/*Ver.2.269.62~*/; {xt,yt}; restore; undefined2var=>xy_eqn; store; {$xt,$yt}=call_xy_eqn0(=<xy_eqn)=>/*Ver.2.269.62~*/; {xt,yt}; restore; {$xt,$yt}=call_xy_eqn1(=<xy_eqn)=>/*Ver.2.269.62~*/; {xt,yt}; |
|
目次
has4test |
最上位関数||name渡し||scope継承参照
clear; set_ans($varName)=<varName=ans; checkV($varName)=<(hass(varName),has(varName),has__(varName)); checkE($eqnName)=<(hass(=<eqnName),has(=<eqnName),has__(=<eqnName)); check($varName,$eqnName)=<(checkV($varName)==>:checkE($eqnName)==>); wrapper0(n)=<({n,n},check($a,$f)=>,{n,n},check($a,$f)==>); (,:wrapper0(0)==>: [a=1,f=<1:wrapper0(1)==>: [a=1,:wrapper0(2)==>: [,f=<1:wrapper0(3)==>: [del__(a),del__(=<f):wrapper0(4)==>]: [last{a=1,add__(a)},add__(=<f):wrapper0(5)==>]: [add__(a),last{f=<1,add__(=<f)}:wrapper0(6)==>]: [del__(a),del__(=<f):wrapper0(7)==>] ]]]); set_ans($ans0)=>; [ wrapper1(n,=<f0,=<f1)=<(f0==>,f1==>:wrapper0(n)==>), /*wrapper1(n,==<f0,==<f1)=<(f0=>,f1=>:wrapper0(n)==>),*/ =<(wrapper1(0,=<0,=<0)==>: [wrapper1(1,=<a=1,=<f=<1)==>: [wrapper1(2,=<a=1,=<0)==>: [wrapper1(3,=<0,=<f=<1)==>: [wrapper1(4,=<del__(a),=<del__(=<f))==>]: [wrapper1(5,=<last{a=1,add__(a)},=<add__(=<f))==>]: [wrapper1(6,=<add__(a),=<last{f=<1,add__(=<f)})==>]: [wrapper1(7,=<del__(a),=<del__(=<f))==>] ]]]) ]=>; set_ans($ans1)=>; double_check=ans1-ans0; |
|
目次
test4 useMutex |
useMutex参照
clear; f=<-1,f=1: [=<f]=>: [f=2,=<f]=>: [f=<-3,=<f]=>: [f=<-4,f=4,=<f]=>: [f=5,f=<-5,=<f]=>: [f=<-6,=<[=<f]]=>; |
|
目次
test4 useStatic |
useStaticScopes2dArray参照
clear; call_f0=()=<[make_f(1)=>,f=>,make_f(2)=>,f=>,make_f(3)=>,f=>]: call_f1=()=<[make_f(1)=>f,f=>,make_f(2)=>f,f=>,make_f(3)=>f,f=>]: make_f=(x)=<[a=1,=<()=<a*x]=>f,call_f0=>: make_f=(x)=<[a=1,=<[a=2,=<()=<a*x]=>]=>f,call_f0=>: make_f=(x)=<[a=1,[a=2,=<()=<a*x]=>f,=<f]=>f,call_f0=>: make_f=(x)=<[a=1,[a=2,=<()=<a*x]=>f,=<f]=>,call_f1=>; |
|
目次
Call-by -Reference |
scope参照参照
clear; set_f(?f)=<[,f=<x]; make_NG=(x)=<[f=<0,set_f(?f)==>,=<f]=>f; [make_NG(1)==>,f=>,[make_NG(2)==>,f=>,make_NG(3)==>,f=>]]; clear; [ arr=(1,2),f=(?arr)=<[arr1=arr,arr1[][1]=-1,],f(?arr)=>,arr: arr=(1,2),f=(?arr)=<[arr1=arr,arr1[][1]=-1,arr=arr1],f(?arr)=>,arr: arr=(1,2),f=(?arr)=<[arr1=arr+0,arr1[][1]=-1,arr=arr1],f(?arr)=>,arr: arr=(1,2),f=(?arr)=<[($arr1)=(=<arr),arr1[][1]=-1,],f(?arr)=>,arr: arr=(1,2),f=(?arr)=<[($arr1)=(=<arr),arr1[][1]=-1,arr=arr1],f(?arr)=>,arr: g=<(1,2),f=(?g)=<[,,g=<(1,-1)],f(?g)=>,g=> ]; clear; CbE_g=(=<f)=<[g(x)=<f(x)=>+1,=<g]=>; CbR_g=(?f)=<[g(x)=<f(x)=>+1,=<g]=>; step_CbE=(=<fdummy)=<CbE_g(=<fdummy)=>f; step_CbR=(?f)=<CbR_g(?f)=>f; [ x=1,x: f(x)=<x,f(x)=>: CbE_g(=<f)=>f,f(x)=>: CbR_g(?f)=>f,f(x)=>: step_CbE(=<f)==>,f(x)=>: step_CbR(?f)=>,f(x)=> ]; clear; A=false; show_A=(=<callback)=<[callback=>,=<A/*cloned*/]=>; [n=0,f=()=<last(n=n+1,n),=<f]=>count; push0=(?A)=<($A)=(=<push1(?A)=>); push1=(?A)=<A.push(count=>); push2=(?A,?B)=<last[A.push(count=>),B.push(count=>)]; show_A(=<[A=false,(?B)=<B.push(A)](?A)=>)=>: show_A(=<(A=(1,2:3,4),(?B)=<push0(?B)=>)(?A)=>)=>: show_A(=<((?A)=<push1(?A)=>)(?A)=>)=>: show_A(=<[(?A)=<push1(?A)=>](?A)=>)=>: show_A(=<[(?A)=<push1(?A)=>](?A)=>)=>: show_A(=<[(?A)=<[(?A)=<push1(?A)=>](?A)=>](?A)=>)=>: show_A(=<[(?B)=<[(?C)=<push1(?C)=>](?B)=>](?A)=>)=>: show_A(=<[(?B)=<((?C)=<push2(?B,?C)=>)(?B)=>](?A)=>)=>: show_A(=<([(?B)=<(?C)=<push2(?B,?C)=>](?A)=>)(?A)=>)=>: show_A(=<([run=<push2(?B,?C)=>,(?B)=<(?C)=<run=>](?A)=>)(?A)=>)=>: show_A(=<([run(?D,?F)=<push2(?D,?F)=>,(?B)=<(?C)=<run(?B,?C)=>](?A)=>)(?A)=>)=>: A; clear; f=<false; recursive_call=(?g,?h)=<h=<g=>+1; call_f=(=<callback)=<[callback=>,=<f=>]=>; call_f(=<[(?f)=<f=<1](?f)=>)=>: call_f(=<[(?f)=<[(?f)=<f=<2](?f)=>](?f)=>)=>: call_f(=<[(?g)=<[(?h)=<h=<3](?g)=>](?f)=>)=>: call_f(=<([(?g)=<(?h)=<recursive_call(?g,?h)==>](?f)=>)(?f)=>)=>: call_f(=<([(?g)=<(?h)=<recursive_call(?g,?h)==>](?f)=>)(?f)=>)=>: call_f(=<([(?g)=<(?h)=<recursive_call(?g,?h)==>](?f)=>)(?f)=>)=>: call_f(=<([(?g)=<(?h)=<recursive_call(?g,?h)==>](?f)=>)(?f)=>)=>: f=>; clear; f=(?a)=<[a,a=a+1]; call_f0=(a)=<[a,f(?a)=>,a,f(?a)==>,a]; call_f1=(?a)=<[a,f(?a)=>,a,f(?a)==>,a]; wrapper=(a0)=<[a0:a=a0,call_f0(a)==>,a:a=a0,call_f1(?a)==>,a]; a=1,wrapper(a)=>,wrapper(a)==>: [ a=2,wrapper(a)=>,wrapper(a)==>: [a=3,wrapper(a)=>,wrapper(a)==>]: [a=4,wrapper(a)=>,wrapper(a)==>] ]; clear; f=(?A)=<[ (A[0]:A[1]): (A[0][0],A[0][1]:A[1][0],A[1][1]): last{A[0][0][sizer(A)][sizec(A)]=A}: A: last{A[1]=A[0],A[][1]=A[][0]}: A ]; A=(1,2:3,4):A::f(?A)=>::A; [A=(1,2:3,4):A::f(?A)=>::A]; |
|
目次
args |
行列要素pattern matching||const宣言||単独scope||式変数への式読出し||式変数のarguments||無名call
||Newton高階行列関数参照 clear; ($c0,$c1,$c2)=(3,4,5); call_f=<(f(c0)=>,f(c1)=>,f(c2)=>); store; [ [(a,b)=<(c)=<a+b+c](1,2)=>f,call_f==>: [a=1,b=2,=<(c)=<a+b+c]=>f,call_f==>: f(c)=<[a=1,b=2,=<a+b+c]=>,call_f==>: f(c)=<last[a=1,b=2,a+b+c],call_f==>: [$f=<0,$a=1,$b=2,=<(c)=<f=>+a+b+c]=>f,call_f==>: f(c)=<[$f=<0,$a=1,$b=2,=<f=>+a+b+c]=>,call_f==>/*Ver.2.261.61~*/: f(c)=<last[$f=<0,$a=1,$b=2,f=>+a+b+c],call_f==>/*Ver.2.261.61~*/ ]; restore; $f(c)=<[a=1,b=2,=<a+b+c]=>,call_f=>: [$f(c)=<[a=2,b=3,=<a+b+c]=>,call_f==>]; restore; [$f=<0,$a=1,$b=2,=<(c)=<f=>+a+b+c]=>$f/*Ver.2.262.61~*/,call_f=>: [[$f=<0,$a=2,$b=3,=<(c)=<f=>+a+b+c]=>$f/*Ver.2.262.61~*/,call_f==>]; clear; a=-1,b=-2,c=-3: [[[(a)=<(b)=<(c)=<(a,b,c)](1)=>](2)=>](3)=>: [[[(a)=<(b)=<(c)=<(a,b,c)](1)==>](2)=>](3)=>: [[[(a)=<(b)=<(c)=<(a,b,c)](1)=>](2)==>](3)=>: [[[(a)=<(b)=<(c)=<(a,b,c)](1)=>](2)=>](3)==>: [(c)=<[(b)=<[(a)=<(a,b,c)](1)=>](2)=>](3)=>: [(c)=<[(b)=<[(a)=<(a,b,c)](1)==>](2)=>](3)=>: [(c)=<[(b)=<[(a)=<(a,b,c)](1)=>](2)==>](3)=>: [(c)=<[(b)=<[(a)=<(a,b,c)](1)=>](2)=>](3)==>; clear; a=-1,b=-2,c=-3: [[[(a)=<(b)=<(c)=<(x,y)=<(a,b,c,x,y)](1)=>](2)=>](3)=>f:f(4,5)=>:f(6,7)=>:f(4,5)==>:f(6,7)==>: [(c)=<[(b)=<[(a)=<(x,y)=<(a,b,c,x,y)](1)=>](2)=>](3)=>f:f(4,5)=>:f(6,7)=>:f(4,5)==>:f(6,7)==>; clear; k=1,x=3, A=linspace(1,2,2:3,4,2)/*(1,2:3,4)*/, f(x)=<x+1,g(x)=<x-2,h(x)=<x*x, compose_x(x)=<h(g(f(x)=>*k)=>*k)=>*k, compose_A(A)=<h(=<g(=<f(=<A)=>*k)=>*k)=>*k, fgh_pipe_x(x,=<f,=<g,=<h) =<[[[(=<F)=<(=<G)=<(=<H)=<H(G(F(x)=>*k)=>*k)=>*k](=<f)=>](=<g)=>](=<h)=>, fgh_nest_x(x,=<f,=<g,=<h) =<[(=<H)=<[(=<G)=<[(=<F)=<H(G(F(x)=>*k)=>*k)=>*k](=<f)=>*k](=<g)=>*k](=<h)=>*k, fgh_pipe_A(A,=<f,=<g,=<h) =<[[[(=<F)=<(=<G)=<(=<H)=<H(=<G(=<F(=<A)=>*k)=>*k)=>*k](=<f)=>](=<g)=>](=<h)=>, fgh_nest_A(A,=<f,=<g,=<h) =<[(=<H)=<[(=<G)=<[(=<F)=<H(=<G(=<F(=<A)=>*k)=>*k)=>*k](=<f)=>*k](=<g)=>*k](=<h)=>*k, A_map_fgh(A,=<f,=<g,=<h) =<A.map((x)=<f(x)=>*k).map((x)=<g(x)=>*k).map((x)=<h(x)=>*k), compose_pipe_x(x)=<fgh_pipe_x(x,=<f,=<g,=<h)=>, compose_nest_x(x)=<fgh_nest_x(x,=<f,=<g,=<h)=>, compose_pipe_A(A)=<fgh_pipe_A(=<A,=<f,=<g,=<h)=>, compose_nest_A(A)=<fgh_nest_A(=<A,=<f,=<g,=<h)=>, pipe_A(A)=<A_map_fgh(=<A,=<f,=<g,=<h)=>: [[[(=<F)=<(=<G)=<(=<H)=<H(G(F(x)=>*k)=>*k)=>*k](=<f)=>](=<g)=>](=<h)=>, [(=<H)=<[(=<G)=<[(=<F)=<H(G(F(x)=>*k)=>*k)=>*k](=<f)=>*k](=<g)=>*k](=<h)=>*k, compose_pipe_x(x)=>,compose_nest_x(x)=>, compose_x(x)=>,compose_A(x)=>,pipe_A(x)=>: [[[(=<F)=<(=<G)=<(=<H)=<H(=<G(=<F(=<A)=>*k)=>*k)=>*k](=<f)=>](=<g)=>](=<h)=>, [(=<H)=<[(=<G)=<[(=<F)=<H(=<G(=<F(=<A)=>*k)=>*k)=>*k](=<f)=>*k](=<g)=>*k](=<h)=>*k, compose_pipe_A(=<A)=>,compose_nest_A(=<A)=>, compose_A(=<A)=>,pipe_A(=<A)=>; clear; h=false; Nmax=20; f(x)=<(x-1)**4=0; g(x)=<(x-1)*(x-2)*(x-3)*(x-4)*(x-5)*(x-6)=0; x0=1.1; args_f=(=<f,=<{x0}); args_g=(=<g,=<{x0}); Newton(args_f):Newton(=<f,=<{x0}); Newton(args_g):Newton(=<g,=<{x0}); make_args(=<f,x0)=<[=<f,=<{x0},h,Nmax]; call_f(x0)=<Newton(make_args(=<f,x0)=>); call_g(x0)=<Newton(make_args(=<g,x0)=>); call_f(1)=>,call_f(2)=>; call_g(1)=>,call_g(2)=>,call_g(3)=>,call_g(4)=>,call_g(5)=>,call_g(6)=>,call_g(7)=>; |
|
目次
curried |
strict-mode||単独scope||式変数への式読出し||無名call参照
clear; f=(=<h)=<h(3)=>; f((x)=<(1,2)*x)=>; g=(x)=<x; f((x)=<x)=>,f(=<g)=>; clear; div=(x,y)=<x/y; div_curried_not_closed=(x)=<(y)=<div(x,y)=>; div_curried_closed_1st_call=(x)=<[(y)=<div(x,y)=>]; (div_curried_not_closed(1)=>)(1)=>; (div_curried_closed_1st_call(2)=>)(1)=>; x=3; (div_curried_not_closed(4)=>)(1)=>; (div_curried_closed_1st_call(5)=>)(1)=>; div_curried_closed_1st_call=(x)=<[(x)=<(y)=<div(x,y)=>](x)=>; inv_y_applied_partially=div_curried_closed_1st_call(1)=>; (1/linspace(1,10,10):linspace(1,10,10)).map((x)=<inv_y_applied_partially(x)=>).; clear; f=(x)=<[(y)=<(z)=<(x,y,z)]; xy_z=(f(1)=>)(2)=>; xy_z(3)=>:xy_z(4)=>:xy_z(5)=>; |
|
目次
closure |
単独scope||無名call||式変数のarguments参照
clear; a=1: [()=<a]()=>,[()=<[()=<a]()=>]()=>,[()=<[(a)=<a](2)=>]()=>,[()=<[a=1,(a)=<a](2)=>]()=>: [=<a]=>,[=<[=<a]=>]=>,[=<[(a)=<a](2)=>]=>,[=<[a=1,(a)=<a](2)=>]=>: [=<[(a)=<last[,a]](3)=>]=>: [=<[a=2,(a)=<last[,a]/*resolved*/](3)=>]=>: [[(a)=<=<last[,a]/*not-resolved*/](3)=>]=>: [[a=2,(a/*not-closed*/)=<=<last[,a]](3)=>]=>: [[a=2,(a/*closed@1st-call*/)=<[=<last[,a]]](3)=>]=>: [[a=2,[(a/*closed@1st-call*/)=<=<last[,a]]](3)=>]=>: [(a)=<=<last[,a]](3)=>f,f=>,f==>: [a=2,(a)=<=<last[,a]](3)=>f,f=>,f==>: [(a)=<()=<last[,a]](3)=>f,f()=>,f()==>: [a=2,(a)=<()=<last[,a]](3)=>f,f()=>,f()==>: [[(a)=<(x,y)=<(a,x,y)](a)=>](2,3)=>: [[a=2,(a/*not-closed*/)=<(x,y)=<(a,x,y)](a)=>](2,3)=>: [[a=2,(a/*closed@1st-call*/)=<[(x,y)=<(a,x,y)]](a)=>](2,3)=>: [[a=2,[(a/*closed@1st-call*/)=<(x,y)=<(a,x,y)]](a)=>](2,3)=>: [[(a)=<(x,y)=<(a,x,y)](a)=>](2,3)=>f/*resolved*/,f=>,f==>: [[a=2,(a)=<(x,y)=<(a,x,y)](a)=>](2,3)=>f/*resolved*/,f=>,f==>; clear; f=<[x=1,f(x)=<x,(a)=<(x)=<f(a*x)=>](2)=>,f=>g,g(3)=>: f(a0)=<[x=1,f(x)=<x,(a)=<(x)=<f(a*x)=>](a0)=>,f(2)=>g,g(3)=>: f(a0)=<[x=1,f(x)=<x,(a)=<(x)=<f(a*x)=>](a0)=>g,f(2)=>,g(3)=>: f(a0)=<[x=1,f(x)=<x,(a/*not-closed*/)=<(x)=<f(a*x)=>](a0)=>,f(2)=>g,g(3)=>: 1,f(-3)=>h,h(3)=>: f(a0)=<[x=1,f(x)=<x,a=-2,(a/*not-closed*/)=<(x)=<f(a*x)=>](a0)=>g,f(2)=>,g(3)=>: 1,f(-3)=>,g(3)=>: f(a0)=<[x=1,f(x)=<x,a=-2,(a/*closed@1st-call*/)=<[(x)=<f(a*x)=>]](a0)=>g,f(2)=>,g(3)=>: f(a0)=<[x=1,f(x)=<x,a=-2,[(a/*closed@1st-call*/)=<(x)=<f(a*x)=>]](a0)=>g,f(2)=>,g(3)=>: 1,f(-3)=>,g(3)=>: f(a0)=<[x=1,f(x)=<x,a=-2,(a/*not-closed*/)=<(x)=<f(a*x)=>](a0)=>,f(2)=>g,g(3)=>: 1,f(-3)=>h,h(3)=>: f(a0)=<[x=1,f(x)=<x,a=-2,(a/*closed@1st-call*/)=<[(x)=<f(a*x)=>]](a0)=>,f(2)=>g,g(3)=>: f(a0)=<[x=1,f(x)=<x,a=-2,[(a/*closed@1st-call*/)=<(x)=<f(a*x)=>]](a0)=>,f(2)=>g,g(3)=>: 1,f(-3)=>h,h(3)=>; clear; a=-1,b=0,x=1: [a=1,[(a)=<(x)=<a*x+b](-3)=>f,=<f]=>f,f(x)=>,f(x)==>: [a=1,[(a)=<(x)=/*disabled*/=<a*x+b](-3)=>f,=<f]=>f,f(x)=>,f(x)==>: [a=1,[(a)=<(x)=<a*x+b](-3)==>f,=<f]=>f,f(x)=>,f(x)==>: [a=1,[(a)=<(x)=<a*x+b](-3)=>f,==<f]=>f,f(x)=>,f(x)==>: [a=1,[(a)=<(x)=<a*x+b](-3)=>f,=<f]==>f,f(x)=>,f(x)==>: [a=1,[a=2,(a/*not-closed*/)=<(x)=<a*x+b](-3)=>f,=<f]=>f,f(x)=>,f(x)==>: [a=1,[a=2,(a/*closed@1st-call*/)=<[(x)=<a*x+b]](-3)=>f,=<f]=>f,f(x)=>,f(x)==>: [a=1,[a=2,[(a/*closed@1st-call*/)=<(x)=<a*x+b]](-3)=>f,=<f]=>f,f(x)=>,f(x)==>; clear; x=i; f=<x; call_f=<(f=>,f==>); call_a(x0)=<[x=x0,call_f==>:($a)=(=<call_f==>)/*Ver.2.269.62~*/,a]; wrapper(x)=<(x:call_a(x)==>:call_a(-x)==>); wrapper_closed(x)=<[x:call_a(x)==>:call_a(-x)==>]; wrapper(0)==>:wrapper_closed(0)==>; [wrapper(1)==>:[wrapper(2)==>:[wrapper(3)==>]]]; [wrapper_closed(1)==>:[wrapper_closed(2)==>:[wrapper_closed(3)==>]]]; clear; call_f=<(hass(=<f)&&&f=>||||false,a); a=i,f=[ a=1,f=[ a=2,f=[ a=3, (a)==<=<call_f](a)=>, =<==<call_f]=>, /*omitted=<*/==<call_f]=>; call_f=>; clear; f=()=<x; call_f=(x0,=<f)=<[ x0: g=<f,x=x0+1,(g=>)=>: g=()=<f,x=x0+2,(g=>)=>: g=<f,x=x0+1,(g==>)=>: g=()=<f,x=x0+2,(g==>)=>: g==<f,x=x0+3,(g=>)=>: g=()==<f,x=x0+4,(g=>)=> ]; x=i; [call_f(0,()=<f)=>: [call_f(0,()=<-x*2)=>: [call_f(f=()=<-x*3,=<f)=>]: [call_f(f=()=<last{not(hass(x))&&&(x=NaN),-x*3},=<f)=>: [call_f(f=()=<last[not(hass(x))&&&(x=NaN),-x*4],=<f)=>]] ]]; |
|
目次
counter |
単独scope||式変数への式読出し||無名call参照
clear; [ c0=-1: make_counter=(c0,dc0)=<[c=c0,dc=dc0/*mutable*/,=<()=<last(c=c+dc,c)]()=>: make_counter(0,1)=>count0: count0=>,count0=>,count0=>: make_counter(100,3)=>count1: count1=>,count1=>,count1=>,count0=>,count0=>,count0=>: make_counter_closed_1st_call=(c0,dc0)=<[c=c0,(dc)/*immutable*/=<()=<last(c=c+dc,c)](dc0)=>: make_counter_closed_1st_call(0,1)=>count0: count0=>,count0=>,count0=>: make_counter_closed_1st_call(100,3)=>count1: count1=>,count1=>,count1=>,count0=>,count0=>,count0=>: make_counter_closed_1st_call=(c0,dc0)=<[(c,dc)/*immutable*/=<()=<last(c=c+dc,c)](c0,dc0)=>: make_counter_closed_1st_call(0,1)=>count0: count0=>,count0=>,count0=>: make_counter_closed_1st_call(100,3)=>count1: count1=>,count1=>,count1=>,count0=>,count0=>,count0=>: make_counter_closed_1st_call=(c0,dc0)=<[c=c0,(dc)/*immutable*/=<()=<last[c=c+dc,c/*closed*/]](dc0)=>: make_counter_closed_1st_call(0,1)=>count0: count0=>,count0=>,count0=>: make_counter_closed_1st_call(100,3)=>count1: count1=>,count1=>,count1=>,count0=>,count0=>,count0=>: [arr=[],_r(=<arr=(arr,count0=>),,10),=<arr]=>: c0 ]; |
|
目次
push |
method演算子参照
clear; A=(1,2:3,4:); B={-1:-2,-3}; C=(A,5); v=(1,2); f(x)=<x; g(x)=<x*x; N=3; arr_f=[ ()=<_r(=<arr.unshift(B),arr=A,N): ()=<_r(=<arr[-1].unshift(B),arr=A,N): ()=<_r(=<arr[-#arr-1].unshift(B),arr=A,N): ()=<_r(=<arr.push(B),arr=A,N): ()=<_r(=<arr[-1].push(B),arr=A,N): ()=<_r(=<arr[#arr].push(C),arr=[],N): ()=<_r(=<arr[__n__-1].push(C),arr=[],N): ()=<_r(=<arr[__n__].push(C),arr=A,N) ]; check(n)=<[(arr_f[n-1])==>,=<arr]=>; check(1)=>; check(2)=>; check(3)=>; check(4)=>; check(5)=>; check(6)=>; check(7)=>; check(8)=>; v.unshift(=<f),(v)[][0](3)=>; v.shift(); v.push((x)=<x),(v)[][2](3)=>; v.pop(); v.push(=<g),(v.)[2](3)=>; v.pop(); v.unshift((x)=<x*x),(v.)[0](3)=>; v.shift(); v; v[#v].push((3,4:5)); v; v.flip(); v; |
|
目次
map |
iterator演算子||座標形式行列関数||式変数への式読出し参照
clear; A0=(1,2,3:4,5,6); A=(A0:-A0); cooA=mat2coo(A); Amn=cooA[0]; arr_m=cooA[1]; arr_n=cooA[2]; f0(x)=<abs(x); f1(x,i_,j_,self)=<x%2&&&-x|||self[i_][j_]/*x*/; cond0(x)=<x<0; cond1(x)=<abs(x)==3; /*f1(x,i_,j_,self)=<switch(x%2,-x:1,x);*/ A_mapped=A.map((x)=<abs(x)).map((x,i_,j_,self)=<x%2&&&-x|||self[i_][j_]); A_filtered=A_mapped.filter((x)=<x<0); A_filter0_4chain=A_mapped.filter0((x)=<x<0); Aij=A_filtered[0]; arr_i=A_filtered[1]; arr_j=A_filtered[2]; A.map(=<f0).map(=<f1).filter(=<cond0); A.map(=<f0).map(=<f1).filter(=<cond1); (A.map(=<f0).map(=<f1).filter(=<cond0))[0].filter(=<cond1); ((A.map(=<f0).map(=<f1).filter(=<cond0))[0].filter(=<cond1))[0]; A.map(=<f0).map(=<f1).filter0(=<cond0).filter0(=<cond1); clear; a=1; f(x)=<x; call_f_pipe0(=<f_)=<f_(a)=>; call_f_pipe1(=<f_)=<(f_=>)(a)=>; call_f_pipe2(=<f_)=<((f_=>)=>)(a)=>; [=<f]=>g,call_f_pipe0(=<g)=>; [=<{=<f}/*=<f*/]=>g,call_f_pipe0(=<g)=>; [=<{=<=<f}]=>g,call_f_pipe1(=<g)=>; [=<{=<=<=<f}]=>g,call_f_pipe2(=<g)=>; ([=<{(x)=<(x)}]=>,[=<{=<f}/*=<f*/]=>,[=<f]=>).map(=<call_f_pipe0); ([=<{=<(x)=<(x)}]=>,[=<{=<=<f}]=>).map(=<call_f_pipe1); ([=<{=<=<(x)=<(x)}]=>,[=<{=<=<=<f}]=>).map(=<call_f_pipe2); f0_p0(x)=<x; f0_p0(a)=>; call_f_pipe0(=<f0_p0)=>; call_f_pipe1(=<=<f0_p0)=>; call_f_pipe2(=<=<=<f0_p0)=>; ((x)=<x:=<f0_p0).map(=<call_f_pipe0); f0_p1=<(x)=<x; f1_p1=<=<f; f2_p1=<(=<f); (f0_p1=>)(a)=>; (f1_p1=>)(a)=>; (f2_p1=>)(a)=>; (=<(x)=<x,=<=<f,=<(=<f):=<f0_p1,=<f1_p1,=<f2_p1).map(=<call_f_pipe1); (=<=<f0_p0).map(=<call_f_pipe1); f0_p2=<=<(x)=<x; f1_p2=<=<=<f; f2_p2=<(=<=<f); ((f0_p2=>)=>)(a)=>; ((f1_p2=>)=>)(a)=>; ((f2_p2=>)=>)(a)=>; (=<=<(x)=<x,=<=<=<f,=<(=<=<f):=<f0_p2,=<f1_p2,=<f2_p2).map(=<call_f_pipe2); (=<=<f0_p1,=<=<f1_p1,=<=<f2_p1).map(=<call_f_pipe2); (=<=<=<f0_p0).map(=<call_f_pipe2); clear; $a=3; $f(x)=<x,$g(x)=<-x,$h(x)=<x*x; fgh0_strict(sw)=<(=<(x)=<f(x)=>:=<(x)=<g(x)=>:=<(x)=<h(x)=>)[sw]=>; fgh1_strict(sw)=<(=<=<f:=<=<g:=<=<h)[sw]=>; fgh2_strict(sw)=<(=<sw==0&&&(=<f)|||sw==1&&&(=<g)|||sw==2&&&(=<h))=>; fgh3(sw)=<(=<f:=<g:=<h)[sw]=>; fgh4(sw)=<(sw==0&&&(=<f)|||sw==1&&&(=<g)|||sw==2&&&(=<h))=>; store; [ call_f(=<f_)=<(f_=>)(a)=>, callback(=<f_)=<call_f(=<f_)=>, call_map(=<list_eqn,=<callback)=<(list_eqn=>).map(=<callback), call_filter(=<list_eqn,=<callback)=<(list_eqn=>).filter(=<callback), call_filter0(=<list_eqn,=<callback)=<(list_eqn=>).filter0(=<callback), (=<list_eqn)=<( ((list_eqn=>)=>/*tail-return*/)(a)=>: (0,1,2).map((sw)=<call_f(=<(list_eqn[sw]=>)=>)=>): (0,1,2).map((sw)=<call_f(=<(list_eqn=>)[sw]=>)=>): call_map(=<list_eqn,=<callback)=>.: call_filter(=<list_eqn,(=<f_)=<abs(call_f(=<f_)=>)==3)=>list_eqn_filtered: call_map(=<list_eqn_filtered[0]=>,=<callback)=>: call_filter0(=<list_eqn,(=<f_)=<abs(call_f(=<f_)=>)==3)=>list_eqn_filtered0: call_map(=<list_eqn_filtered0=>,=<callback)=> ) ](=<(=<(x)=<f(x)=>:=<(x)=<g(x)=>:=<(x)=<h(x)=>))=>; restore; [ call_f(=<f_)=<f_(a)=>, call_sw(sw,=<fgh)=<[fgh(sw)=>f,call_f(=<f)=>,call_f((a)=<(fgh(sw)=>)(a)=>)=>], (=<list_eqn)=<[ arr=[], (list_eqn=>).map((=<fgh)=<(0,1,2).map((sw)=<arr=(arr:call_sw(sw,=<fgh)=>))), =<arr]=> ](=<(=<fgh0_strict,=<fgh1_strict,=<fgh2_strict,=<fgh3,=<fgh4))=>; restore; call_fgh(a,=<fgh)=<[fgh($f)=>f,fgh($g)=>g,fgh($h)=>h,=<[f(a)=>,g(a)=>,h(a)=>]]=>; make_f0($eqnName)=<[($eqnName)=<(x)=<eqnName(x)=>]($eqnName)=>; make_f1($eqnName)=<[($eqnName)=<()=<eqnName]($eqnName)=>; make_f2($eqnName)=<[($eqnName)=<eqnName]($eqnName)=>; push_arr4vecr(=<f_,i_,j_)=<arr=[arr:call_fgh(a*(j_+1),=<f_)=>]; push_arr4vecc(=<f_,i_)=<arr=[arr:call_fgh(a*(i_+1),=<f_)=>]; 0: call_fgh(a*1,=<make_f0)=>: call_fgh(a*2,=<make_f1)=>: call_fgh(a*3,=<make_f2)=>: 1: [arr=[],(=<make_f0,=<make_f1,=<make_f2).map(==<push_arr4vecr),=<arr]=>: 2: [arr=[],{=<make_f0,=<make_f1,=<make_f2}.map(==<push_arr4vecc)./*vecc->vecr*/,=<arr]=>: 3: [arr=[],temp={=<make_f0,=<make_f1,=<make_f2}.map(==<push_arr4vecc)/*->0*/,=<arr]=>; clear; $f(x)=<x,$g(x)=<-x,$h(x)=<x*x; (x)=<x,(x)=<-x,(x)=<x*x; A=ans; [ [=<f,=<g,=<h].map((=<f)=<f(3)=>): [(x)=<x,(x)=<-x,(x)=<x*x].map((=<f)=<f(3)=>): A.map((=<f)=<f(3)=>): A.filter((=<f)=<(lt(f(3)=>,0))): A.filter0((=<f)=<(gt(f(3)=>,0))).map((=<g)=<g(3)=>) ]; clear; f=(A)=<A,f(=<(1,2))=>,f(=<(1))=>,f((1))=>: A_not_iterable=(x)=<x,A_not_iterable(2)=>: A_iterable=((x)=<x),(A_iterable[0][0])(2)=>,(A_iterable)(2)=>: A_iterable=((x)=<x,(x)=<-x,(x)=<x*x),(A_iterable[0][0])(2)=>,(A_iterable)(2)=>: A_lazy=((x)=<x,(x)=<-x,(x)=<x*x),f(A)=<((A[0][0])(2)=>,(A)(2)=>),f(=<A_lazy)=>; clear; $A_lazy=(=<1,=<2:=<3,=<4); anonymous_call=(A_lazy/*tail-return*/)=>; $A=((A_lazy[0][0])=>,(A_lazy[0][1])=>:(A_lazy[1][0])=>,(A_lazy[1][1])=>); f=(A_iterable)=<[=<A_iterable.map((=<f)=<f=>)]=>; f(=<A_lazy)=>; f(=<A_lazy[0])=>:f(=<A_lazy[1])=>; f(=<A_lazy[][0])=>,f(=<A_lazy[][1])=>; f(=<(=<1,=<2:=<3,=<4))=>; f(=<(=<1,=<2:=<3,=<4)[0])=>:f(=<(=<1,=<2:=<3,=<4)[1])=>; f(=<(=<1,=<2:=<3,=<4)[][0])=>,f(=<(=<1,=<2:=<3,=<4)[][1])=>; clear; $a=1; $A=((x)=<a*x,(x)=<-a*x,(x)=<a*x*x); [ $a=2: A.map((=<f)=<f(3)=>): A.map((=<f)=<f(3)==>): [arr=[],A.map((=<f)=<arr=(arr,f(3)=>,f(3)==>)),=<arr]=> ]; |
|
目次
arr_ext |
遅延評価||型定義の問題点参照
clear; A_lazy=[=<1,=<[2,3],=<[4,=<[5,=<x]]]; (((A_lazy[][2])=>)[][1])=>; ((([=<1,=<[2,3],=<[4,=<[5,=<x]]][][2])=>)[][1])=>; ((((A_lazy[][2])=>)[][1])=>)[][1]; (((([=<1,=<[2,3],=<[4,=<[5,=<x]]][][2])=>)[][1])=>)[][1]; tA_lazy=[=<1,=<[2,3].,=<[4,=<[5,=<x].].].; (((tA_lazy[2])=>)[1])=>; (((([=<1,=<[2,3].,=<[4,=<[5,=<x].].].)[2])=>)[1])=>; ((((tA_lazy[2])=>)[1])=>)[1]; ((((([=<1,=<[2,3].,=<[4,=<[5,=<x].].].)[2])=>)[1])=>)[1]; |
|
目次
reshapez |
reshape行列関数参照
・3次元の未知変数vectorとz-x平面を相互変換する関数(行||列vectorで記述) clear; reshapez_(x:Nxy)=<[arr=[], isRow=(#x===1), isCol=(##x===1), Nz=(isRow||isCol)&&&###x/Nxy, isRow&&&(x=x.), push_arr(dj)=<_r(=<arr.push(x[(__n__-1)*Nxy+dj]),,Nz), Nz%1===0&&&_r(=<push_arr(__n__-1)=>,,Nxy), isCol&&&(arr=arr.), =<arr]=>; ($Nx,$Ny,$Nz)=(2,3,4); Nxyz=Nx*Ny*Nz; x0=linspace(1,Nxyz,Nxyz); x1=reshapez_(=<x0:Nx*Ny)=>; =reshapez(x0:Nx*Ny); x0=reshapez_(=<x1:Nz)=>; =reshapez(x1:Nz); x1y=reshapec(x1:Nz*Nx,Ny); get_x1yj(j)=<reshapec(x1y[][j]:[Nz,Nx]); x1y0=get_x1yj(0)=>; x1y1=get_x1yj(1)=>; x1y2=get_x1yj(2)=>; x1=_r((arr)=<(arr,reshapec(get_x1yj(__n__-1)=>:[1,Nz*Nx])),=<[],Ny); x1=trans(reshapez_(=<trans(x0):Nx*Ny)=>); =trans(reshapez(trans(x0):Nx*Ny)); |
|
目次
Rump |
誤差の扱い参照
clear; ($a,$b,$ans_correct)=(77617.0,33096.0,-0.8273960599468214); get_terms(a,b)=<{333.75*b**6,a**2*11*(a*b)**2,-a**2*b**6,-a**2*121*b**4,-a**2*2,5.5*b**8,a/(2*b)}; terms=get_terms(a,b)=>; check_last=(last(terms)=sum(terms.)); [ polynomial=<333.75*b**6+a**2*(11*(a*b)**2-b**6-121*b**4-2)+5.5*b**8+a/(2*b), polynomial_expanded=<333.75*b**6+a**2*11*(a*b)**2-a**2*b**6-a**2*121*b**4-a**2*2+5.5*b**8+a/(2*b), Rump_s_example(a,b)=<(polynomial=>,polynomial_expanded=>,sum(terms.),ans_correct), get_terms_normalized=<[term_min=min(abs(terms).),=<abs(terms)./term_min]=>, calc_decimal_digits(vecr,=<callback)=<round(log10(callback(=<vecr)=>)+1), =<(Rump_s_example(a,b)=>.: nvecr=get_terms_normalized=>, decimal_digits_min=calc_decimal_digits(=<nvecr,(vecr)=<min(vecr))=>, decimal_digits_max=calc_decimal_digits(=<nvecr,(vecr)=<max(vecr))=>, decimal_digits_needed=decimal_digits_max-decimal_digits_min: decimal_digits_min,decimal_digits_max,decimal_digits_needed ) ]=>; |
|
目次
Fibonacci |
再帰call参照
clear; [ F0=0, F1=1, arr=[F0,F1], [F0=F0,F1=F1,eqn=()=<last{F2=F0+F1,F0=F1,F1=F2,F2},=<eqn]=>generator_fibo2, _s((n)=<arr.push(generator_fibo2=>),2,10), =<arr ]=>; clear; fibok(n,n0,k)=<n<k-1&&n0||||n<k|||_s((m)=<fibok(n-m,n0,k)=>,1,k); luca2(n)=<fibok(n,2,2)=>; [ fibon_se(N,n0,k,ns_,ne_)=<[arr=[],_s((n)=<arr=(arr,fibok(n,n0,k)=>),ns_,ne_),=<arr]=>, fibonk_se(N,n0,ks,ke)=<[arr=[],_s((k)=<arr=(arr:fibon_se(N,n0,k,0,N)=>),ks,ke),=<arr]=>, fibok_se(N,n0,ks,ke)=<[arr=[],_s((k)=<arr=(arr,fibok(N,n0,k)=>),ks,ke),=<arr]=>, fibok_fill_n0(N,n0,ks,ke)=<( fibonk_se(N,n0,ks,ke)=>: fibok_se(N,n0,2,N)=>: [arr=[],_s((k)=<arr=(arr,fibok(N,n0,k)=>),ks,ke),=<arr]=> ), (N)=<[ (N,n0s,n0e,ks,ke)=<[ arr=[],_s((n0)=<arr=(arr:n0:fibok_fill_n0(N,n0,ks,ke)=>),n0s,n0e),=<arr]=> ](N,0,3,2,N)=> ](10)=>/*exponential-time*/; |
|
目次
fact |
階乗関数参照
clear; fact_(n)=<n<=1|||n*fact_(n-1)=>; [ fact_sw0(n)=<n<=1|||n*fact_sw1(n-1)=>, fact_sw1(n)=<n*fact_sw0(n-1)=>, (N)=<( (N/2)!,fact(N/2),N!,fact(N): fact_(N)=>,fact_sw0(N)=>,fact_sw1(N)=>: A=linspace(1,N,N).map((n)=<fact_(n)=>): mat2coo(A):: A.map((x)=<-x).map((x)=<abs(x)).filter((x)=<x>fact(N/2)) )](10)=>; |
|
目次
gcd/lcm |
gcd/lcm関数参照
clear; gcd_(a0,b0)=<last[ a=a0,b=b0,_r((n)=<last{ia=round(a),ib=round(b),a=ia<0||ib===0&&&ia|||ib,b=ia%(ib||1)}, isBreak_a=<isNaN(a)|||a<0&&&~~(a=false),1e6,=<{isBreak_a=>|||b==0}),a]; lcm_(a,b)=<a*(b/gcd_(a,b)=>); [gcd(111,222,333,444,555),gcd_(111,gcd_(222,gcd_(333,gcd_(444,555)=>)=>)=>)=>: lcm(111,222,333,444,555),lcm_(111,lcm_(222,lcm_(333,lcm_(444,555)=>)=>)=>)=>]; |
|
目次
random |
その他の乱数参照
clear; PRNG_LCG(a,b,m,x0,N)=<[ arr=(x0), [x=x0,eqn=<last{x=(a*x+b)%m,x},=<eqn]=>gen_rand, _r(=<arr.push(gen_rand=>),,min(N,m-1)), =<arr ]=>; PRNG_LCG(6,0,11,1,10)=>; ($m,$x0,$N)=(0x7fffffff,1,10); [ PRNG_LCG(16807,0,m,x0,N)=>: PRNG_LCG(48271,0,m,x0,N)=>: PRNG_LCG(0x7FFFFFED,0x7FFFFFC3,m,x0,N)=> ]; clear; shuffle_FY(?tarr)=<last[ len=sizer(tarr), switch_arr=(i1)=<last{i0=floor(rand()*(i1+1)),w=tarr[i1],tarr[i1]=tarr[i0],tarr[i0]=w}, _s((i_)=<switch_arr(i_)=>,len-1,1) ]; [(N)=<[tarr=linspace(0,N-1,N).,shuffle_FY(?tarr)=>,=<tarr.]=>](2)=>; clear; rand_table(csv)=<last[ table=sort0(csv), ymin=min(table)[0],ymax=max(table)[0], y=ymin+(ymax-ymin)*rand(), x=interp(y:table),x]; [Pinv_y=( -0.999999427,-0.999936657,-0.997300203,-0.954499736,-0.682689492,0, 0.682689492,0.954499736,0.997300203,0.999936657,0.999999427: -5,-4,-3,-2,-1,0,1,2,3,4,5 ), N=1,arr=[],_r((n)=<arr.push(rand_table(=<Pinv_y)=>),,N),=<arr.]=>; |
|
目次
average |
averageぼかし参照
clear; [isSquare=0,N=3,N2=int(N/2),filter=vectorc(N*N), calc_w(s2)=<switch(isSquare==0,switch(s2>N2**2,0:1,1):1,1), _s((ir)=<{_s((ic)=<filter[(ir+N2)*N+(ic+N2)]=calc_w(ir**2+ic**2)=>,-N2,N2)},-N2,N2), =<trans(filter)]=>; |
|
目次
average _asym |
非対称averageぼかし参照
clear; [isSquare=0,N=13,N2=int(N/2),filter=vectorc(N*N), x=1,y=2,k=3,rad=pi/4, rotz_LHS(psi)=<{rt=real(psi),=<(cos(rt),sin(rt),:-sin(rt),cos(rt),:,,1)}=>, Rz=rotz_LHS(rad)=>, isOutOfArea(x)=<switch( isSquare==0,x[0]**2+(x[1]*k)**2>N2**2: 1,(x[0]**2>N2**2)|((x[1]*k)**2>N2**2) ), calc_w(ir,ic)=<switch(isOutOfArea(=<Rz*{ic-x,ir-y,1})=>,0:1,1), _s((ir)=<{_s((ic)=<filter[(ir+N2)*N+(ic+N2)]=calc_w(ir,ic)=>,-N2,N2)},-N2,N2), =<trans(filter)]=>; |
|
目次
Gaussian |
Gaussぼかし参照
clear; [isStrict=0,N=3,N2=int(N/2),filter=vectorc(N*N),Nbit=N-1,wmax=2**Nbit, calc_w(s2)=<switch(isStrict==0,round(wmax*exp(-0.5*s2)):1,exp(-0.5*s2)), _s((ir)=<{_s((ic)=<filter[(ir+N2)*N+(ic+N2)]=calc_w(ir**2+ic**2)=>,-N2,N2)},-N2,N2), =<trans(filter)]=>; |
|
目次
plot2d{} _multi |
代数学準拠の問題点参照
clear; x_long=(1+2i)*(1,2,3,4,5,6,7,8,9,10); y_long=2*x_long; x_short=(1+2i)*(1,2,3,4,5); y_short=4*x_short; xt_OK={x_long,x_short}; yt_OK={y_long,y_short}; xt_OK={x_short,x_long}; yt_OK={y_short,y_long}; xt={x_short,x_long,x_long,2*x_short}; yt={y_short,y_long,2*y_short,y_long}; {xt,yt}; trans(ans); |
|
目次
plot2d _interp |
補間関数参照
clear; plot2d_interp(Nx,Nt)=<[ out=<{xt,yt}, scope2storage=<last{add__(xt),add__(yt)},
init=<last{
x=linspace(0,2*pi,Nx+1), xn=linspace(0,2*pi,Nt+1), table=(xn:trans(sin(trans(xn)))) },
run=<last{
init=>,run=>,return=out=>,scope2storage=>,
table[1]=(1+2i)*table[1], table_sorted_key0=sort0(table), xt=(table[0]:x), yt=(table[1]:interp0(x:table_sorted_key0):interp1(x:table_sorted_key0): interp2(x:table_sorted_key0):interp3(x:table_sorted_key0)) }, =<return]=>; plot2d_interp(last{Nx=21,Nx},Nx>>1)=>; |
|
目次
plot2d _fft1d |
高速Fourier変換参照
clear; $radix=2; deg=4; N=radix**deg; arr_n=linspace(0,N-1,N); ($n0,$n1,$n2)=N/(2,4,8); ($A0,$A1,$A2)=1/(1,2,3)+i; f(t)=<(A0,A1,A2)*{e^((i*n0*t)*2*pi/N),e^((i*n1*t)*2*pi/N),e^((i*n2*t)*2*pi/N)/2}; f_samples=f(=<arr_n)=>; F_FFT=fft1d(f_samples); f_IFFT=ifft1d(F_FFT); F_DFT=[]; f_IDFT=[]; DFT(n)=<_s((t)=<f(t)=>*e^((-i*n*t)*2*pi/N),0,N-1); IDFT(t)=<_s((n)=<F_DFT[][n]*e^((i*n*t)*2*pi/N),0,N-1)/N; arr_n.map((n)=<F_DFT.push(DFT(n)=>)); arr_n.map((n)=<f_IDFT.push(IDFT(n)=>)); xt=arr_n; yt=((f_samples:f_IDFT:f_IFFT):(F_DFT:F_FFT)/N); |
|
目次
plot2d() _multi |
代数学準拠の問題点参照
clear; x_long={1,2,3,4,5,6,7,8,9,10}*(1+2i); y_long=x_long*2; x_short={1,2,3,4,5}*(1+2i); y_short=x_short*4; xt_OK=(x_long,x_short); yt_OK=(y_long,y_short); xt_NG=(x_short,x_long); yt_NG=(y_short,y_long); x_short_mod={1,2,3,4,5,NaN,NaN,NaN,NaN,NaN}*(1+2i); y_short_mod=x_short_mod*4; xt_OK=(x_short_mod,x_long); yt_OK=(y_short_mod,y_long); xt=(x_short_mod,x_long,x_long,x_short_mod*2); yt=(y_short_mod,y_long,y_short_mod*2,y_long); (xt,yt); trans(ans); |
|
目次
plot2d _circle |
plot2d-from-arr参照
clear; plot2d_circle(t0,t1,N,M)=<[ out=<(xt,yt), scope2storage=<last{add__(xt),add__(yt)},
init=<last{
tn=<t0+(t1-t0)*n/N, xt=zeros(N+1,M+1),yt=zeros(N+1,M+1) },
run=<last{
init=>,run=>,return=out=>,scope2storage=>,
stepnm=<last{tn=tn=>,xt[n][m]=cos(tn)*m,yt[n][m]=sin(tn)*m}, casesM=<_s((m)=<stepnm=>,0,M), evolutionN=<_s((n)=<casesM=>,0,N), evolutionN=> }, =<return]=>; plot2d_circle(0,2*pi,10,3)=>; |
|
目次
plot2d _evolution |
plot2d-from-arr参照
clear; plot2d_evolution(t0,t1,dt,z_x0,z_v0,z_u,m,kCdA_sphere)=<[ out=<(xt,yt), scope2storage=<last{add__(xt),add__(yt)},
init=<last{
g=-9.8,z_a=0+g*i, t=0, x_initial=<{z_x0,z_v0}, f(t,z_x,z_v)=<{z_v,z_a+(kCdA_sphere/m)*(z_u-z_v)}, N=round((t1-t0)/dt),M=0, xt=zeros(N+1,M+1),yt=zeros(N+1,M+1) },
run=<last{
init=>,run=>,return=out=>,scope2storage=>,
dtn=<n<=0&&0||||dt/*switch(n<=0,0:1,dt)*/, x_next=x_initial=>, step=<last{dt0=dtn=>,x_next=_o(=<f,=<{x_next},t+[,dt0]),t=t+dt0}, stepnm=<last{step=>,z_x=x_next[0],xt[n][mdummy]=real(z_x),yt[n][mdummy]=imag(z_x)}, casesM=<_s((mdummy)=<stepnm=>,0,M)/*m-reserved*/, evolutionN=<_s((n)=<casesM=>,0,N), evolutionN=> }, =<return]=>; plot2d_evolution(0,5,0.5,0,20+20i,0,1,1)=>; |
|
目次
plot2d _Lagrange |
Lagrange補間参照
clear; plot2d_Lagrange(x,y)=<[ out=<(xt,yt), scope2storage=<last{add__(xt),add__(yt)},
init=<last{
N=min(sizer(x),sizer(y))-1, dx=x[1][0][N][1]-x, xt=(x+dx/2)[0][0][N][1], yt=zeros(N,1) },
run=<last{
init=>,run=>,return=out=>,scope2storage=>,
ljx(j,x_)=<_p((m)=<m==j&&&1|||(x_-x[m])/(x[j]-x[m]),0,N), Lkx(x_)=<_s((j)=<y[j]*ljx(j,x_)=>,0,N), _s((i_)=<yt[i_]=Lkx(xt[i_])=>,0,N-1), yinterp=interp2(trans(xt):trans(x,y)), xt=(x,xt), yt=(y,yt,trans(yinterp)) }, =<return]=>; plot2d_Lagrange(=<{0,1,2,3,4,5,6,7,8,9},=<{1,3,2,5,0,-3,-2,-5,-1,-1}*(1+2i))=>; |
|
目次
plot2d _nspline |
spline補間参照
clear; nspline3d(x,y)=<[ out=<(u),
init=<last{
N=min(sizer(x),sizer(y))-1, dx=x[1][0][N][1]-x, dy=y[1][0][N][1]-y, r=vectorc(3*N), coo=zeros(3,10*N-4) },
run=<last{
init=>,run=>,return=out=>,
_s((j)=<last{ n=j+1,j0=3*j,dxi=dx[j],dyi=dy[j], coo[0][j0][1][3]=(dxi,dxi**2,dxi**3), coo[1][j0][1][3]=(n,n,n), coo[2][j0][1][3]=(n,N+n,2*N+n), r[j]=dyi },0,N-1), _s((j)=<last{ n=j+1,j0=3*N+4*j,dxi=dx[j], coo[0][j0][1][4]=(1,-1,2*dxi,3*dxi**2), coo[1][j0][1][4]=(N+n,N+n,N+n,N+n), coo[2][j0][1][4]=(n,n+1,N+n,2*N+n) },0,N-2), _s((j)=<last{ n=j+1,j0=7*N+3*j-4,dxi=dx[j], coo[0][j0][1][3]=(1,-1,3*dxi), coo[1][j0][1][3]=(2*N+n-1,2*N+n-1,2*N+n-1), coo[2][j0][1][3]=(N+n,N+n+1,2*N+n) },0,N-2), j0=10*N-4-3, coo[0][j0][1][3]=(1,1,3*dx[N-1]), coo[1][j0][1][3]=(3*N-1,3*N,3*N), coo[2][j0][1][3]=(N+1,2*N,3*N), u=Gauss_coo(coo:trans(r)) }, =<return]=>; plot2d_nspline(x,y)=<[ out=<(xt,yt), scope2storage=<last{add__(xt),add__(yt)},
init=<last{
N=min(sizer(x),sizer(y))-1, dx=x[1][0][N][1]-x, xt=(x+dx/2)[0][0][N][1], yt=zeros(N,1) },
run=<last{
init=>,run=>,return=out=>,scope2storage=>,
u=nspline3d(=<x,=<y)=>, b=u[0][0][N][1], c=u[N][0][N][1], d=u[2*N][0][N][1], _s((i_)=<last{ dxi=xt[i_]-x[i_], yt[i_]=y[i_]+b[i_]*dxi+c[i_]*dxi**2+d[i_]*dxi**3 },0,N-1), yinterp=interp3(trans(xt):trans(x,y)), xt=(x,xt), yt=(y,yt,trans(yinterp)) }, =<return]=>; plot2d_nspline(=<{0,1,2,3,4,5,6,7,8,9},=<{1,3,2,5,0,-3,-2,-5,-1,-1}*(1+2i))=>; |
|
目次
plot2d _bspline |
spline補間参照
clear; bspline2d(x,y,i_,t)=<[ out=<(xy),
init=<last{
Si(i_,t)=<0.5*(t^2,t,1)*(1,-2,1:-2,2,0:1,1,0)*{(x[i_-1],y[i_-1]),(x[i_],y[i_]),(x[i_+1],y[i_+1])} },
run=<last{
init=>,run=>,return=out=>,
xy=Si(i_,t)=> }, =<return]=>; plot2d_bspline(x,y)=<[ out=<(xt,yt), scope2storage=<last{add__(xt),add__(yt)},
init=<last{
N=min(sizer(x),sizer(y))-1, M=N-1, xt=zeros(N+1,M), yt=zeros(N+1,M) },
run=<last{
init=>,run=>,return=out=>,scope2storage=>,
_s((m)=<_s((n)=<last{ ($xnm,$ynm)=bspline2d(=<x,=<y,m,n/N)=>, xt[n][m-1]=xnm, yt[n][m-1]=ynm },0,N),1,M), xt=(x,xt), yt=(y,yt) }, =<return]=>; plot2d_bspline(=<{0,1,2,3,2},=<{1,4,2,4,4}*(1+2i))=>; |
|
目次
SND/P(x)/ erf(x)/erfc(x) |
特殊関数参照
clear; NI=100; SND(t)=<exp(-t^2/2)/sqrt(2*pi); arr_args=[ (x)=<_i((t)=<SND(t)=>,[0,x],NI)*2,(x)=<_i((t)=<SND(t)=>,[0,x*sqrt2],NI)*2,(x)=<1-erf(x)=>: (x)=<_i0((t)=<SND(t)=>,[0,x],NI)*2,(x)=<_i0((t)=<SND(t)=>,[0,x*sqrt2],NI)*2,(x)=<1-erf(x)=>: (x)=<_o45((t,x)=<SND(t)=>,,[0,x],NI)*2,(x)=<_o45((t,x)=<SND(t)=>,,[0,x*sqrt2],NI)*2,(x)=<1-erf(x)=> ]; f(=<P,=<erf,=<erfc)=<[x=3,SND(x)=>,P(x)=>,erf(x)=>,erfc(x)==>]; _r((arr)=<(arr:f(arr_args[__n__-1])=>),=<[],#arr_args); |
|
目次
cSND/cP |
特殊関数参照
clear; NI=50; cSND(z)=<exp(-abs(z)^2)/pi; arr_integral=[ (=<f,a,b)=<_i(=<f,a,b,NI): (=<f,a,b)=<_i0(=<f,a,b,NI): (=<f,a,b)=<_o45((t,x)=<f(t)=>,,a,b,NI) ]; f(==<integral_)=<[ cP_z(z)=<integral_((y)=<integral_((x)=<cSND(x+(y)i)=>,0,real(z))=>*2,0,imag(z))=>*2, cP_r(r)=<integral_((t)=<integral_((r)=<cSND(r*e^(i*t))=>,0,r)=>,0,2*pi)=>/sqrt(pi), =<(z=3*(1+i)/sqrt2,cSND(z)=>,cP_z(z)=>,cP_r(abs(z))=>)]=>; _r((arr)=<(arr:f(arr_integral[__n__-1])=>),=<[],#arr_integral); |
|
目次
residue |
clear;
integral_C(=<f,z,r,n)=<_r((s)=<s+last[dt=2*pi/n,t=(__n__-1)*dt,a=z+r*e**(i*t),b=z+r*e**(i*(t+dt)),_i(==<f,a,b)],,n); integral_C((z)=<1/(z-0.5i),0,1,10)=>; |
|
目次
integral |
積分の数値解法||時間発展の解法参照
・調整箇所 ・Ver.2.819.132以降、対応箇所 clear; check(=<f,a,b,NI,type)=<(_o45((t,x)=<f(t)=>,,a,b,NI):_i(=<f,a,b,NI):_i0(=<f,a,b,NI,type)); NI=100; check((x)=<floor(min(x/0.3,1)),0,1,NI,)=>:0.7; check((x)=<sqrt(x),0,1,NI,)=>:2/3; check((x)=<1/(x**4+x**2+0.9),-1,1,NI,)=>:1.58223296372967293312; check((x)=<2/(2+sin(31.4159*x)),0,1,NI,)=>:1.15470066904371304341; check((x)=<sin(314.159*x)/(3.14159*x),0.1,1,NI,)=>:0.0090986452565692970698; check((x)=<sqrt(50)*exp(-50*3.14159*x**2),0,10,NI,)=>:0.500000211166100039341; check((x)=<50*(sin(50*3.14159*x)/(50*3.14159*x))**2,eps,1,NI,)=>:0.4989872301695; check((x)=<cos(cos(x)+3*sin(x)+2*cos(2*x)+3*sin(2*x)+3*cos(3*x)),0,pi,NI,)=>:0.8386763426944296; check((x)=<1/(x**2+1.005),-1,1,NI,)=>:1.564396444069049773091; check((x)=<cosh(10*(x-0.2))**(-2)+cosh(100*(x-0.4))**(-4)+cosh(1000*(x-0.6))**(-6),0,1,NI,)=>:0.2108027355005492773756; check((x)=<exp(-x)/sqrt(x),0,1/2,NI,)=>:1.210035619311; check((x)=<exp(-x)/sqrt(x),1/2,inf,NI,)=>:0.5624182315944; check((x)=<exp(-x)/sqrt(x),,inf,NI,)=>:1.7724538509055; check((x)=<exp(-x)/sqrt(x),0,0,NI,)=>:0; check((x)=<sqrt(tan(x)),0,pi/4,NI,)=>:0.48749549439936104836; check((x)=<sqrt(tan(x)),pi/4,0,NI,)=>:-0.48749549439936104836; sqrt(tan(-1.1102230246251565e-16)); check((x)=<sqrt(tan(x)),pi/4,eps,NI,)=>:-0.48749549439936104836; check((x)=<sqrt(tan(x+eps*i)),pi/4,0,NI,)=>:-0.48749549439936104836; check((x)=<pow(x,2)*exp(x),0,1+i,NI,)=>:-2; check((x)=<pow(x,2)*exp(x),1+i,0,NI,)=>:2; check((x)=<1/x,0,0,NI,)=>:0; check((x)=<1/x,inf,inf,NI,)=>:0; check((x)=<x,inf,inf,NI,)=>:NaN; check((x)=<x,-inf,-inf,NI,)=>:NaN; |
|
目次
integral_DE _quadrature |
・Ver.2.819.132以降、対応箇所
clear; integral_DE_quadrature(==<f,a,b,N,h,opt_type)=<[ arr_x=[ : (t)=<tanh((pi/2)*sinh(t)),(t)=<(pi/2)*cosh(t)/cosh((pi/2)*sinh(t))**2: (t)=<exp(t-exp(-t)),(t)=<exp(t-exp(-t))*(1+exp(-t)): (t)=<exp((pi/2)*sinh(t)),(t)=<exp((pi/2)*sinh(t))*(pi/2)*cosh(t): (t)=<sinh((pi/2)*sinh(t)),(t)=<cosh((pi/2)*sinh(t))*(pi/2)*cosh(t) ], isFinite_(x)=<abs(x)<inf, isInfinite_(x)=<x===inf, isNaN_(x)=<~~isFinite_(x)=>&&&~~isFinite_(f(x)=>)=>, isFF(a,b)=<isFinite_(a)=>&&isFinite_(b)=>/*[a,b]*/, isFI(a,b)=<isFinite_(a)=>&&isInfinite_(b)=>/*[a,inf]*/, isFIm(a,b)=<isFinite_(b)=>&&isInfinite_(a)=>/*[inf,a]*/, isIF(a,b)=<isInfinite_(-a)=>&&isFinite_(b)=>/*[-inf,b]*/, isIFm(a,b)=<isInfinite_(-b)=>&&isFinite_(a)=>/*[b,-inf]*/, isII(a,b)=<isInfinite_(-a)=>&&isInfinite_(b)=>/*[-inf,inf]*/, isIIm(a,b)=<isInfinite_(-b)=>&&isInfinite_(a)=>/*[inf,-inf]*/, hasMinus(a,b)=<isFIm(a,b)=>||isIFm(a,b)=>||isIIm(a,b)=>, hasM=hasMinus(a,b)=>, hasM&&&(w=a,a=b,b=w), type=opt_type|||isFI(a,b)=>||isIF(a,b)=>&&&3|||isII(a,b)=>&&&4|||1, x=arr_x[type][0], xd=arr_x[type][1], abw=(isIF(a,b)=>&&&[-1,b,1]|||type===2||type===3&&&[1,a,1]|||type===4&&&[1,,1]|||[(b-a)/2,(b+a)/2,(b-a)/2]), phi(t,a,b,w)=<[y=f(a*x(t)=>+b)=>*xd(t)=>*w,=<isFinite_(y)=>&&&y]=>, S(a,N,h)=<_s((k)=<phi(k*h,abw)=>,-N/2,N/2)*h, err=(false===0)*(phi((-N/2)*h,abw)=>+phi((N/2)*h,abw)=>)*h, =<cne(a,b)&&&(hasM&&-1||1)*S(a,N,h)=>+err||||~~isNaN_(a)=>&&&0||||NaN+(NaN)i]=>; check(=<f,a,b,NI,type)=<(integral_DE_quadrature(=<f,a,b,NI,10/NI,type)=>:_i0(=<f,a,b,NI,type)); z=1/2; NI=100; args=((x)=<x**(z-1)*exp(-x),0,inf,NI); check(args,4)=>:1.772453850905516027298; check(args,3)=>:1.772453850905516027298; check(args,2)=>:1.772453850905516027298; check(args,1)=>:1.772453850905516027298; check(args,)=>:_i0(args):1.772453850905516027298; check((x)=<x**(z-1)*exp(-x),inf,0,NI,)=>:-1.772453850905516027298; check((x)=<x**(z-1)*exp(-x),1,inf,NI,)=>:0.2788055852806619764993; NI=100; check((x)=<1/(1+(sqrt(x))^3),1+i,inf,NI,)=>:1.500781043410964539996-0.4383480058647808280315i; check((x)=<1/(1+(sqrt(x))^3),inf,1+i,NI,)=>:-1.500781043410964539996+0.4383480058647808280315i; NI=1000; check((x)=<1/(1-x^3),-inf,1+i,NI,)=>:-0.01853195524822145602092-0.2259704060343700453459i; check((x)=<1/(1-x^3),1+i,-inf,NI,)=>:0.01853195524822145602092+0.2259704060343700453459i; NI=1000; check((x)=<1/(1+25*x^2),-inf,inf,NI,)=>:0.6283185307179586476925; check((x)=<1/(1+25*x^2),inf,-inf,NI,)=>:-0.6283185307179586476925; check((x)=<1/(1+25*x^2),-inf,-inf,NI,)=>:0; check((x)=<1/(1+25*x^2),inf,inf,NI,)=>:0; NI=1000; check((x)=<sin(1/sqrt(x))/sqrt(x),0,1,NI,)=>:1.008134123813856743979; check((x)=<sin(1/sqrt(x))/sqrt(x),1,0,NI,)=>:-1.008134123813856743979; NI=100; check((x)=<exp(-x)/sqrt(x),0,1/2,NI,)=>:1.210035619311; check((x)=<exp(-x)/sqrt(x),1/2,inf,NI,)=>:0.5624182315944; check((x)=<exp(-x)/sqrt(x),,inf,NI,)=>:1.7724538509055; check((x)=<exp(-x)/sqrt(x),0,0,NI,)=>:0; NI=100; check((x)=<sqrt(tan(x)),0,pi/4,NI,)=>:0.48749549439936104836; check((x)=<sqrt(tan(x)),pi/4,0,NI,)=>:-0.48749549439936104836; NI=100; check((x)=<pow(x,2)*exp(x),0,1+i,NI,)=>:-2; check((x)=<pow(x,2)*exp(x),1+i,0,NI,)=>:2; NI=100; check((x)=<1/x,0,0,NI,)=>:0; check((x)=<1/x,inf,inf,NI,)=>:0; check((x)=<x,inf,inf,NI,)=>:NaN; check((x)=<x,-inf,-inf,NI,)=>:NaN; NI=20; globalS(=<f)=<integral_DE_quadrature(=<f,0,1,NI,10/NI,)==>; globalS((z)=<globalS((y)=<globalS((x)=<1/(1-x*y*z))==>)==>)==>; globalS(=<f)=<_i0(=<f,0,1,NI); globalS((z)=<globalS((y)=<globalS((x)=<1/(1-x*y*z))==>)==>)==>; 1.2020569031595942; globalS(=<f)=<_i(=<f,0,1,NI); globalS((z)=<globalS((y)=<globalS((x)=<1/(1-x*y*z))==>)==>)==>; globalS(=<f)=<(_t1((t,x)=<f(t)=>,=<{0,},1,NI))[1]; globalS((z)=<globalS((y)=<globalS((x)=<1/(1-x*y*z))==>)==>)==>; globalS(=<f)=<_o1((t,x)=<f(t)=>,,0,1,NI); globalS((z)=<globalS((y)=<globalS((x)=<1/(1-x*y*z))==>)==>)==>; 1.2020569031595942; |
|
目次
matrix _product |
行列積の解法参照
clear; LpR(L,R)=<[product=<LR[ir][ic]=ttL[ir]*(ttR.)[ic]., ttL=L.., ttR=R.., LR=zeros(sizer(ttL),sizec(ttR)), _s((ir)=<_s((ic)=<product=>,0,sizec(ttR)-1),0,sizer(ttL)-1), =<LR]=>; [L=(1,2:3:4,5:6),R=(1,2:3,4,5),=<LpR(=<L,=<R)=>]=>; |
|
目次
rotationx/y/z |
特殊仕様行列関数参照
clear; rotx(phi)=<[rt=real(phi),=<(1,,:,cos(rt),-sin(rt):,sin(rt),cos(rt))]=>; roty(theta)=<[rt=real(theta),=<(cos(rt),,sin(rt):,1,:-sin(rt),,cos(rt))]=>; rotz(psi)=<[rt=real(psi),=<(cos(rt),-sin(rt),:sin(rt),cos(rt),:,,1)]=>; [t=pi/4,=<[rotx(t)=>,roty(t)=>,rotz(t)=>]]=>; |
|
目次
rotationx/y/z _LHS |
特殊仕様行列関数参照
clear; rotx_LHS(phi)=<[rt=real(phi),=<(1,,:,cos(rt),sin(rt):,-sin(rt),cos(rt))]=>; roty_LHS(theta)=<[rt=real(theta),=<(cos(rt),,-sin(rt):,1,:sin(rt),,cos(rt))]=>; rotz_LHS(psi)=<[rt=real(psi),=<(cos(rt),sin(rt),:-sin(rt),cos(rt),:,,1)]=>; [t=pi/4,=<[rotx_LHS(t)=>,roty_LHS(t)=>,rotz_LHS(t)=>]]=>; |
|
目次
quaternion |
clear;
q2m_(a,b,c,d)=<(a+(b)i,c+(d)i:-c+(d)i,a-(b)i); m2q_(a,b:c,d)=<((a+d)/2,(a-d)/2i,(b-c)/2,(b+c)/2i); qmul_(q1,q2)=<m2q_(q2m_(q1)=>*q2m_(q2)=>)=>; qnorm_(q)=<sqrt(sum(q*q)); qnormalize_(q)=<q/qnorm_(=<q)=>; qconjugate_(q)=<[cq=-q,cq[][0]=-cq[][0],=<cq]=>; i4=identity(4); check_table=<[ arr=[], _s((m)=<_s((n)=<arr=(arr:qmul_(=<i4[m-1],=<i4[n-1])=>),1,4),1,4), =<arr]=>; check_table=>; _r((arr)=<(arr,qnorm_(=<i4[__n__-1])=>),=<[],#i4); qnormalize_(=<i4[0]*3)=>; q1=(1,2,3,4); q2=(-1,2,-3,4); q1_times_q2=qmul_(=<q1,=<q2)=>; conj_q1_times_q2=qconjugate_(=<q1_times_q2)=>; =qmul_(=<qconjugate_(=<q2)=>,=<qconjugate_(=<q1)=>)=>; nq1=qnormalize_(=<q1)=>; norm_nq1=qnorm_(=<nq1)=>; cq1=qconjugate_(=<q1)=>; =m2q_(q2m_(q1)=>')=>; q1_times_cq1=qmul_(=<q1,=<cq1)=>; cq1_times_q1=qmul_(=<cq1,=<q1)=>; norm_q1=qnorm_(=<q1)=>; =sqrt(q1_times_cq1[][0]); |
|
目次
solvex _Gauss |
Gaussの消去法||連立線形方程式の解法参照
clear; solvex_Gauss(A,b)=<[ out=<x,
init=<last{sizeA=size(A),x=zeros(sizeA,1)},
run=<last{
init=>,run=>,return=out=>,
compare=<last{absA_comp=abs(A[ir_comp][ir]), switch(absA_pivot<absA_comp,=<last{ir_pivot=ir_comp,absA_pivot=absA_comp})}, proc=<{w=A[ir],A[ir]=A[ir_pivot],A[ir_pivot]=w,w=b[ir],b[ir]=b[ir_pivot],b[ir_pivot]=w}, pivotting(ir)=<last{ir_pivot=ir,absA_pivot=abs(A[ir][ir]), _s((ir_comp)=<compare=>,ir+1,sizeA-1),switch(ir<>ir_pivot,=<proc)}, forward=<last{k=A[ir][ic]/A[ic][ic],A[ir]=A[ir]-k*A[ic],b[ir]=b[ir]-k*b[ic]}, backward=<last{r=b[ir],_s((ic)=<r=r-A[ir][ic]*x[ic],ir+1,sizeA-1),x[ir]=r/A[ir][ir]}, _s((ic)=<(pivotting(ic)=>,_s((ir)=<forward=>,ic+1,sizeA-1)),0,sizeA-2), x[sizeA-1]=b[sizeA-1]/A[sizeA-1][sizeA-1],_s((ir)=<backward=>,sizeA-2,0) }, =<return]=>; [rand_Ab=<last{N=5,A=zeros(N,N),b=vectorc(N),gen_rand=<rand()+rand()*i, _s((ir)=<last{_s((ic)=<A[ir][ic]=gen_rand=>,0,N-1),b[ir]=gen_rand=>},0,N-1)}, rand_Ab=>,=</*optimized*/Gauss(A,b)-solvex_Gauss(=<A,=<b)=>]=>; |
|
目次
solvex _Gauss_coo |
Gaussの消去法||座標形式行列関数||spline補間参照
clear; [aA=(1,1,-2,1+i,3i,1,1-i,-1,-i),mA=(1,1,2,2,2,3,3,4,4),nA=(1,2,1,2,3,1,3,3,4), b={4,5,6,7i},coo=(aA:mA:nA),A=coo2mat(coo), =<Gauss(A,b)-Gauss_coo(coo:trans(b))]=>; [aA=(1,1,1,1,1,1,1,-1,2,3,1,-1,3,1,1,3), mA=(1,1,1,2,2,2,3,3,3,3,4,4,4,5,6,6), nA=(1,3,5,2,4,6,1,2,3,5,3,4,5,3,4,6), b={2,-1,0,0,0,0},coo=(aA:mA:nA),A=coo2mat(coo), =<Gauss(A,b)-Gauss_coo(coo:trans(b))]=>; |
|
目次
solvex _pivotting |
連立線形方程式の解法参照
clear; solvex_pivotting(A,b)=<[ out=<x,
init=<last{sizeA=size(A),x=zeros(sizeA,1)},
run=<last{
init=>,run=>,return=out=>,
compare=<switch(abs(A[ir][ir])<abs(A[ir_comp][ir]),=<ir_pivot=ir_comp), proc=<{w=A[ir],A[ir]=A[ir_pivot],A[ir_pivot]=w,w=b[ir],b[ir]=b[ir_pivot],b[ir_pivot]=w}, forward=<last{k=A[ir][ic]/A[ic][ic],A[ir]=A[ir]-k*A[ic],b[ir]=b[ir]-k*b[ic]}, backward=<x[ir]=(b[ir]-A[ir]*x)/A[ir][ir], pivotting(ir)=<_s((ir_comp)=<last{ir_pivot=ir,compare=>,switch(ir<>ir_pivot,=<proc)},ir+1,sizeA-1), _s((ic)=<(pivotting(ic)=>,_s((ir)=<forward=>,ic+1,sizeA-1)),0,sizeA-2), _s((ir)=<backward=>,sizeA-1,0) }, =<return]=>; [A=(i,2,3i:4,5i,6:7i,8,9i),b={1,2i,4},=<solvex_pivotting(=<A,=<b)=>]=>; |
|
目次
solvex _no_pivotting |
連立線形方程式の解法参照
clear; solvex_no_pivotting(A,b)=<[ out=<x,
init=<last{sizeA=size(A),x=zeros(sizeA,1)},
run=<last{
init=>,run=>,return=out=>,
forward=<last{k=A[ir][ic]/A[ic][ic],A[ir]=A[ir]-k*A[ic],b[ir]=b[ir]-k*b[ic]}, backward=<x[ir]=(b[ir]-A[ir]*x)/A[ir][ir], _s((ic)=<_s((ir)=<forward=>,ic+1,sizeA-1),0,sizeA-2), _s((ir)=<backward=>,sizeA-1,0) }, =<return]=>; [A=(i,2,3i:4,5i,6:7i,8,9i),b={1,2i,4},=<solvex_no_pivotting(=<A,=<b)=>]=>; |
|
目次
solvex _iteration |
連立線形方程式の解法参照
clear; solvex_iteration(A,b)=<[ out=<x_solved,
init=<last{sizeA=size(A),sizerb=sizer(b),sizecb=sizec(b),isRow=sizerb<sizecb},
run=<last{
init=>,run=>,return=out=>,
isRow&&&(f=<(__x__.)*A=b)||||(f=<A*(__x__)=b), x_solved=Newton(=<f,=<{b*0},Nmax=1e3,Nmax,1e-10,1) }, =<return]=>; A=(i,2,3i:4,5i,6:7i,8,9i); b={1,2i,4}; tA=A.; tb=b.; xr=solvex_iteration(=<tA,=<tb)=>/*(xr*tA)=(tb)*/; xc=solvex_iteration(=<A,=<b)=>/*{A*xc}={b}*/; double_check=(norm((tb)-(xr*tA)):normc({b}-{A*xc})); |
|
目次
solveAinv |
逆行列の解法参照
clear; solveAinv(A)=<[ out=<Ainv,
init=<last{sizeA=size(A),x0=vectorc(sizeA*sizeA)},
run=<last{
init=>,run=>,return=out=>,
f=<reshape(__x__:sizeA,sizeA)*A=identity(sizeA), x_solved=Newton(=<f,=<{x0},Nmax=1e3,Nmax,1e-10,1), Ainv=reshape(x_solved:sizeA,sizeA) }, =<return]=>; [A=(i,2,3i:4,5i,6:7i,8,9i),=<solveAinv(=<A)=>]=>; |
|
目次
solvex _linear |
Newton法||Gaussの消去法||連立線形方程式の解法参照
clear; ($t,$k,$b)=(2,4,=<{100,320}); A=(1,1:t,k); [y=(b[1]-t*b[0])/(k-t),x=b[0]-y,=<(x,y)]=>: Gauss(A,b).: Newton((x,y)=<{x+y=b[0],t*x+k*y=b[1]}).: Newton((x,y)=<A*{x,y}=b).: Newton((x,y)=<((x,y)*A.).=b).: Newton((x,y)=<(x,y)*A.=b.): Newton(=<A*__x__=b,=<{,}).: Newton(=<__x__.*A.=b.,=<(,)); |
|
目次
solvex _non_linear |
連立非線形方程式の解法参照
clear; solvex_non_linear(==<f_,=<x_initial_)=<[ out=<x_solved,
init=<last{0},
run=<last{
init=>,run=>,return=out=>,
x_solved=Newton(=<f_,=<x_initial_,Nmax=1e3,Nmax,1e-10,1) }, =<return]=>; [f=<{__x__[0]^i-2*__x__[1]=3i,3*__x__[0]+exp(__x__[1])=5i},=<solvex_non_linear(=<f,=<{1+i,1-i})=>]=>; |
|
目次
solvex _bisection |
連立非線形方程式の解法参照
clear; solvex_non_linear(==<f_,=<x_initial_)=<[ out=<x_solved,
init=<last{0},
run=<last{
init=>,run=>,return=out=>,
x_solved=Newton(=<f_,=<x_initial_,Nmax=1e3,Nmax,1e-10,1) }, =<return]=>; solvex_bisection(=<f_,x0,x1,N)=<[ out=<x0,
init=<last{epsf=1e-7,isBreak=<isNaN(x0)|||norm(y0)<epsf},
run=<_r((n)=<last{
init=>,run=>,return=out=>,
x=(x0+x1)/2, y=f_(x)=>, y0=f_(x0)=>, y1=f_(x1)=>, sign(y)==sign(y0)&&&(x0=x)||||sign(y)==sign(y1)&&&(x1=x), x0},,N,=<isBreak), =<return]=>; global_n=1e3+1; global_base=2**(log2(3)-7/4); store; f(x0)=<last[left=global_n*pow(global_base,x0),right=1,=right-left]; [N=1e2,a=0,b=100, =<{solvex_non_linear(=<f,=<{0})=>, solvex_bisection(=<f,a,b,N)=>, solvex_bisection(=<f,b,a,N)=>, solvex_bisection(=<f,a,a,N)=>, solvex_non_linear((x0)=<1-global_n*pow(global_base,x0),=<{0})=>, solvex_bisection((x0)=<1-global_n*pow(global_base,x0),a,b,N)=>, solvex_bisection((x0)=<1-global_n*pow(global_base,x0),b,a,N)=>, solvex_bisection((x0)=<1-global_n*pow(global_base,x0),a,a,N)=>}]=>; restore; [N=1e2,a=0,b=100,f(x0)=<1-global_n*pow(global_base,x0), =<{solvex_non_linear(=<f,=<{0})=>, solvex_bisection(=<f,a,b,N)=>, solvex_bisection(=<f,b,a,N)=>, solvex_bisection(=<f,a,a,N)=>, solvex_non_linear((x0)=<1-global_n*pow(global_base,x0),=<{0})=>, solvex_bisection((x0)=<1-global_n*pow(global_base,x0),a,b,N)=>, solvex_bisection((x0)=<1-global_n*pow(global_base,x0),b,a,N)=>, solvex_bisection((x0)=<1-global_n*pow(global_base,x0),a,a,N)=>}]=>; |
|
目次
solvex _polynomial |
連立非線形方程式の解法参照
clear; step=(==<f_,x0,?arr)=<last[ solvex=<Newton(=<f_,=<{x0},Nmax=1e3,Nmax,eps), arr[0].push(x0), arr[1].push(solvex=>)], f=(x)=<(x-0)*(x-1)*(x-2)*(x-3)*(x-4)*(x-5)*(x-6)=0; generate_initial_value=<6*rand(); _r(=<step(=<f,generate_initial_value=>,?arr)=>,arr=[],1e2); arr_sorted=sort0(arr),($xt,$yt)=(=<arr_sorted[0],=<arr_sorted[1]); |
|
目次
implicit Euler_method |
時間発展の解法参照
Euler_method(t,dt,z_x00,z_v00,z_u,m,kCdA_sphere,isImplicit)=<[ out=<{t_total,x_solved}, scope2storage=<last{add__(z_x0),add__(z_v0),add__(t_total)},
init=<last{
switch(has__(t_total)==0,=<last{t_total=0,z_x0=z_x00,z_v0=z_v00}), g=-9.8,z_a=0+g*i, x_initial=<{z_x0,z_v0}, switch( isImplicit, =<f(z_x,z_v)=<{(z_x-z_x0)/dt=z_v,m*((z_v-z_v0)/dt)=m*z_a+kCdA_sphere*(z_u-z_v)}: 1/*else-explicit*/, =<f(z_x,z_v)=<{(z_x-z_x0)/dt=z_v0,m*((z_v-z_v0)/dt)=m*z_a+kCdA_sphere*(z_u-z_v0)} ), orderT=1, epsN=max(eps*1e3,pow(dt,orderT)), isRelative_epsN=1, relative_epsN=(epsN,isRelative_epsN)/*(epsN,flag)*/ },
run=<last{
init=>,run=>,return=out=>,scope2storage=>,
args_Newton=(=<f,=<x_initial,Nmax=1e3,Nmax,relative_epsN)/*(args)*/, step_iteration=<x_solved=Newton(args_Newton), step_post=<{$z_x0,$z_v0}=x_solved, step=<last{step_iteration=>,step_post=>}, evolution=<_r((n)=<step=>,N=round(t/dt),N), evolution=>, t_total=t_total+N*dt }, =<return]=>; [cond_error=(has__(t_total)==0)&has__(z_x0), proc=<[args=(1,0.5,0,20+20i,0,1,1),=<Euler_method(args,1)=>]=>, =<switch(cond_error==0,=<proc:1,-999/*error-code*/)]=>; |
|
目次
explicit Euler_method |
時間発展の解法参照
[cond_error=(has__(t_total)==0)&has__(z_x0), proc=<[args=(1,0.5,0,20+20i,0,1,1),=<Euler_method(args,0)=>]=>, =<switch(cond_error==0,=<proc:1,-999/*error-code*/)]=>; |
|
目次
explicit ODE_RK4 |
時間発展の解法参照
ODE_RK4(t,dt,z_x00,z_v00,z_u,m,kCdA_sphere)=<[ out=<{t_total,x_next}, scope2storage=<last{add__(z_x0),add__(z_v0),add__(t_total)},
init=<last{
switch(has__(t_total)==0,=<last{t_total=0,z_x0=z_x00,z_v0=z_v00}), g=-9.8,z_a=0+g*i, x_initial=<{z_x0,z_v0}, f(t,z_x,z_v)=<{z_v,z_a+(kCdA_sphere/m)*(z_u-z_v)} },
run=<last{
init=>,run=>,return=out=>,scope2storage=>,
x_next=x_initial=>, stepN=<last{N=round(t/dt),x_next=_o(=<f,=<{x_next},t_total+[,dt*N],N)}, step_post=<{$z_x0,$z_v0}=x_next, evolution=<last{stepN=>,step_post=>}, evolution=>, t_total=t_total+N*dt }, =<return]=>; [cond_error=(has__(t_total)==0)&has__(z_x0), proc=<[args=(1,0.5,0,20+20i,0,1,1),=<ODE_RK4(args)=>]=>, =<switch(cond_error==0,=<proc:1,-999/*error-code*/)]=>; |
|
目次
explicit ODE_fixed |
時間発展の解法参照
・任意stageのButcher-tableに対する固定stepの陽的Runge-Kutta法(公式と一意対応の最短表記) clear; ODE_fixed(t0,x0,table)=<[ order=##table[-1], get_arr_f(t0,x0)=<[ stage_x_sum(i_)=<_r((x)=<x+dt*table[i_][__n__]*arr_f[__n__-1],=<x0,#arr_f), _r(=<arr_f[#arr_f].push(f(t0+dt*table[__n__-1][0],stage_x_sum(__n__-1)=>)=>.),arr_f=[],order), =<arr_f]=>, x=_r((x)=<x+dt*table[-1]*get_arr_f(t0+dt*(__n__-1),=<x)=>,=<x0,Niteration), t=t0+dt*Niteration, =<(t,x)]=>; dt=0.1*(1+i); Niteration=10; table_Butcher=(0:1/2,1/2:1/2,0,1/2:1,0,0,1:1/6,1/3,1/3,1/6); {$t0,$x0,$v0}={,,}; f(t,x,v)=<{v,t+(F-k*x-c*v)/m}; ($F,$m,$k,$c)=(1,1,1,0.4); args=(=<f,=<{t0,x0,v0},t0+dt*Niteration,Niteration); ODE_fixed(t0,=<(x0,v0),=<table_Butcher)=>:(_t0(args,,=<table_Butcher).):(_t(args).); |
|
目次
explicit ODE_adaptive |
時間発展の解法参照
・任意stageのButcher-tableに対する適応stepの陽的Runge-Kutta法 clear; ODE_adaptive(t0,x0,table)=<[ dt0=dt, t=t0, x=x0, order=##table[-1], isAdaptive=eq(#table-order,2), get_arr_f(dt,t0,x0)=<[ stage_x_sum(i_)=<_r((x)=<x+dt*table[i_][__n__]*arr_f[__n__-1],=<x0,#arr_f), _r(=<arr_f[#arr_f].push(f(t0+dt*table[__n__-1][0],stage_x_sum(__n__-1)=>)=>.),arr_f=[],order), =<arr_f]=>, define_step_fixed=<step(n)=<last{ arr_f=get_arr_f(dt,t,=<x)=>, x=x+dt*table[-1]*arr_f, t=t+dt }, define_step_adaptive=<step(n)=<last{ pNdt=0, t00=t, x00=x, dt=dt0/Ndt, _r(=<last{ arr_f=get_arr_f(dt,t,=<x)=>, fc_o5=table[-2]*arr_f, fc_o4=table[-1]*arr_f, cr_norm=norm(fc_o4-fc_o5), sw=cr_norm>=hdelta, pNdt=sw&&1||0, x=x+dt*fc_o5, t=t+dt },sw=false,Ndt,=<{sw}), dt=dt0, cr_norm<=hdelta/10&&&(pNdt=-1), Ndt=max(1,Ndt*2**pNdt), pNdt===1&&&(t=t00,x=x00,step(n)=>) }, Ndt=1, hdelta=abs(dt)*delta, isAdaptive&&&define_step_adaptive=>||||define_step_fixed=>, _r(=<step(__n__)=>,,Niteration), Ndt%1===0&&&(t=t0+dt*Niteration), =<(t,x)]=>; dt=0.1*(1+i); Niteration=10; delta=1e-7; table_fixed=(0:1/2,1/2:1/2,0,1/2:1,0,0,1:1/6,1/3,1/3,1/6); table_adaptive=(0:1/4,1/4:3/8,3/32,9/32:12/13,1932/2197,-7200/2197,7296/2197: 1,439/216,-8,3680/513,-845/4104:1/2,-8/27,2,-3544/2565,1859/4104,-11/40: 16/135,0,6656/12825,28561/56430,-9/50,2/55:25/216,0,1408/2565,2197/4104,-1/5,0); {$t0,$x0,$v0}={,,}; f(t,x,v)=<{v,t+(F-k*x-c*v)/m}; ($F,$m,$k,$c)=(1,1,1,0.4); args=(=<f,=<{t0,x0,v0},t0+dt*Niteration,Niteration); ODE_adaptive(t0,=<(x0,v0),=<table_fixed)=>:(_t0(args,,=<table_fixed).):(_t4(args).); ODE_adaptive(t0,=<(x0,v0),=<table_adaptive)=>:(_t0(args,delta,=<table_adaptive).):(_t45(args,delta).); |
|
目次
DFT1d |
離散Fourier変換の解法参照
clear; DFT1d(f)=<[ out=<f,
init=<last{N=sizer(f),Nf=1,Ni=1/N,F=zeros(N,1)},
run=<last{
init=>,run=>,return=out=>,
F(u)=<{_s((x)=<f[x]*e^(-i*u*x*2*pi/N),0,N-1)*Nf}, _s((u)=<F[u]=F(u)=>,0,N-1), f(x)=<{_s((u)=<F[u]*e^(i*x*u*2*pi/N),0,N-1)*Ni}, _s((x)=<f[x]=f(x)=>,0,N-1) }, =<return]=>; [f={1,2,3,4}*(1+i), =<DFT1d(=<f)=>]=>; |
|
目次
DFT2d_xy |
離散Fourier変換の解法参照
clear; DFT2d_xy(f)=<[ out=<f,
init=<last{N=sizer(f),M=sizec(f),Nf=1,Ni=1/N,Mf=1,Mi=1/M,F=zeros(N,M)},
run=<last{
init=>,run=>,return=out=>,
F(u,v)=<{_s((y)=<{_s((x)=<f[x][y]*e^(-i*u*x*2*pi/N),0,N-1)*Nf}*e^(-i*v*y*2*pi/M),0,M-1)*Mf}, _s((v)=<_s((u)=<F[u][v]=F(u,v)=>,0,N-1),0,M-1), f(x,y)=<{_s((v)=<{_s((u)=<F[u][v]*e^(i*x*u*2*pi/N),0,N-1)*Ni}*e^(i*y*v*2*pi/M),0,M-1)*Mi}, _s((y)=<_s((x)=<f[x][y]=f(x,y)=>,0,N-1),0,M-1) }, =<return]=>; [f={1,2,3,4:5,6,7,8}*(1+i), =<DFT2d_xy(=<f)=>]=>; |
|
目次
DFT2d_yx |
離散Fourier変換の解法参照
clear; DFT2d_yx(f)=<[ out=<f,
init=<last{N=sizer(f),M=sizec(f),Nf=1,Ni=1/N,Mf=1,Mi=1/M,F=zeros(N,M)},
run=<last{
init=>,run=>,return=out=>,
F(v,u)=<{_s((x)=<{_s((y)=<f[x][y]*e^(-i*v*y*2*pi/M),0,M-1)*Mf}*e^(-i*u*x*2*pi/N),0,N-1)*Nf}, _s((u)=<_s((v)=<F[u][v]=F(v,u)=>,0,M-1),0,N-1), f(y,x)=<{_s((u)=<{_s((v)=<F[u][v]*e^(i*y*v*2*pi/M),0,M-1)*Mi}*e^(i*x*u*2*pi/N),0,N-1)*Ni}, _s((x)=<_s((y)=<f[x][y]=f(y,x)=>,0,M-1),0,N-1) }, =<return]=>; [f={1,2,3,4:5,6,7,8}*(1+i), =<DFT2d_yx(=<f)=>]=>; |
|
目次
DWT1d |
離散Wavelet変換の解法参照
clear; DWT1d(w)=<[ out=<w,
init=<last{N=sizer(w),W=zeros(N,1),p=round(log2(N))},
run=<last{
init=>,run=>,return=out=>,
W(w,N)=<_s((t)=<last{ a=w[2*t],b=w[2*t+1],W[t]=a+b,W[t+N2]=a-b },N2=N>>1,N2-1), _r((n)=<last{W(=<w,first{Np,Np=Np>>1})=>,w=W},Np=1<<p,p), buffer=W, w(W,N2)=<_s((t)=<last{ a=W[t],b=W[t+N2],w[2*t]=0.5*(a+b),w[2*t+1]=0.5*(a-b) },0,N2-1), _r((n)=<last{w(=<W,first{Np,Np=Np<<1})=>,W=w},Np=1,p), W=buffer }, =<return]=>; [w={1,2,3,4}*(1+i), =<DWT1d(=<w)=>]=>; |
|
目次
DWT2d_xy |
離散Wavelet変換の解法(列代入)参照
clear; DWT2d_xy(w)=<[ out=<w,
init=<last{N=sizer(w)/*N>1*/,M=sizec(w),W=zeros(N,M),
p=round(log2(N)),q=round(log2(M))},
run=<last{
init=>,run=>,return=out=>,
W_row(w,N)=<_s((t)=<last{ a=w[2*t],b=w[2*t+1],W[t]=a+b,W[t+N2]=a-b },N2=N>>1,N2-1), W_col(w,N)=<_s((t)=<last{ a=w[][2*t],b=w[][2*t+1],W[][t]=a+b,W[][t+N2]=a-b },N2=N>>1,N2-1), _r((n)=<last{W_row(=<w,first{Np,Np=Np>>1})=>,w=W},Np=1<<p,p), _r((n)=<last{w=W,W_col(=<w,first{Nq,Nq=Nq>>1})=>},Nq=1<<q,q), buffer=W, w_row(W,N2)=<_s((t)=<last{ a=W[t],b=W[t+N2],w[2*t]=0.5*(a+b),w[2*t+1]=0.5*(a-b) },0,N2-1), w_col(W,N2)=<_s((t)=<last{ a=W[][t],b=W[][t+N2],w[][2*t]=(a+b)*0.5,w[][2*t+1]=(a-b)*0.5 },0,N2-1), w=W, _r((n)=<last{w_row(=<W,first{Np,Np=Np<<1})=>,W=w},Np=1,p), _r((n)=<last{W=w,w_col(=<W,first{Nq,Nq=Nq<<1})=>},Nq=1,q), W=buffer }, =<return]=>; [w={1,2,3,4:5,6,7,8}*(1+i), =<DWT2d_xy(=<w)=>]=>; |
|
目次
DWT2d_yx |
離散Wavelet変換の解法(列代入)参照
clear; DWT2d_yx(w)=<[ out=<w,
init=<last{N=sizer(w),M=sizec(w)/*M>1*/,W=zeros(N,M),
p=round(log2(N)),q=round(log2(M))},
run=<last{
init=>,run=>,return=out=>,
W_row(w,N)=<_s((t)=<last{ a=w[2*t],b=w[2*t+1],W[t]=a+b,W[t+N2]=a-b },N2=N>>1,N2-1), W_col(w,N)=<_s((t)=<last{ a=w[][2*t],b=w[][2*t+1],W[][t]=a+b,W[][t+N2]=a-b },N2=N>>1,N2-1), _r((n)=<last{W_col(=<w,first{Nq,Nq=Nq>>1})=>,w=W},Nq=1<<q,q), _r((n)=<last{w=W,W_row(=<w,first{Np,Np=Np>>1})=>},Np=1<<p,p), buffer=W, w_row(W,N2)=<_s((t)=<last{ a=W[t],b=W[t+N2],w[2*t]=0.5*(a+b),w[2*t+1]=0.5*(a-b) },0,N2-1), w_col(W,N2)=<_s((t)=<last{ a=W[][t],b=W[][t+N2],w[][2*t]=(a+b)*0.5,w[][2*t+1]=(a-b)*0.5 },0,N2-1), w=W, _r((n)=<last{w_col(=<W,first{Nq,Nq=Nq<<1})=>,W=w},Nq=1,q), _r((n)=<last{W=w,w_row(=<W,first{Np,Np=Np<<1})=>},Np=1,p), W=buffer }, =<return]=>; [w={1,2,3,4:5,6,7,8}*(1+i), =<DWT2d_yx(=<w)=>]=>; |
|
目次
MaclaurinN |
Taylor級数・Maclaurin級数の解法参照
clear; MaclaurinN(=<f_,x,N)=<_s((n)=<_d((x)=<f_=>,0,n)*x^n/n!,0,N); last[f=<exp(x),MaclaurinN(=<f,2,5)=>]; |
|
目次
TaylorN |
Taylor級数・Maclaurin級数の解法参照
clear; TaylorN(=<f_,a,x,N)=<_s((n)=<_d((x)=<f_=>,a,n)*(x-a)^n/n!,0,N); last[f=<exp(x),TaylorN(=<f,0,2,5)=>]; |
|
目次
FourierN |
Fourier級数の解法参照
・Ver.2.809.131以降、omega導入と周期関数f(x)の定義域の更新箇所 clear; FourierN_sym(==<ft_,x,N)=<last[ NI=300, cn(n)=<_i((t)=<(ft_=>)*e^(-i*(n)*t),[-pi,pi]/1,NI)/(2*pi)/*t=[-pi,pi]*/, _s((n)=<(cn(n)=>)*e^(i*(n)*x),-N,N)/*omega=1*/ ]; last[ft=<e^(i*(2.5)*t),FourierN_sym(=<ft,2,5)=>]; FourierN_sym(=<f,x,omega,N)=<last[ NI=300, T=2*pi/omega, cn(n)=<_i((t)=<(f(t)=>)*e^(-i*(n*omega)*t),[-pi,pi]/omega,NI)/T, _s((n)=<(cn(n)=>)*e^(i*(n*omega)*x),-N,N) ]; FourierN_sym((t)=<e^(i*(2.5)*t),2,1,5)=>; FourierN(=<f,x,omega,N)=<last[ isSym=false, NI=300, T=2*pi/omega, cn(n)=<_i((t)=<(f(t)=>)*e^(-i*(n*omega)*t),isSym&&&[-T,T]/2|||[0,T],NI)/T, _s((n)=<(cn(n)=>)*e^(i*(n*omega)*x),-N,N) ]; FourierN((t)=<e^(i*(2.5)*t),2,1,5)=>; FourierN(=<f,x,omega,N)=<last[ isSym=false, NI=300, T=2*pi/omega, cn(n)=<_i0((t)=<(f(t)=>)*e^(-i*(n*omega)*t),isSym&&&[-T,T]/2|||[0,T],NI)/T, _s((n)=<(cn(n)=>)*e^(i*(n*omega)*x),-N,N) ]; FourierN((t)=<e^(i*(2.5)*t),2,1,5)=>; FourierN(=<f,x,omega,N)=<last[ isSym=false, NI=300, T=2*pi/omega, cn(n)=<_o45((t,x)=<(f(t)=>)*e^(-i*(n*omega)*t),,isSym&&&[-T,T]/2|||[0,T],NI)/T, _s((n)=<(cn(n)=>)*e^(i*(n*omega)*x),-N,N) ]; FourierN((t)=<e^(i*(2.5)*t),2,1,5)=>; |
|
目次
zeta _Euler -Maclaurin |
clear;
zeta_Euler_Maclaurin(s,n,m)=<last[ Bn(n)=<n==0|||-_s((k)=<combin(n+1,k)*Bn(k)=>,0,n-1)/(n+1), Tkn(k,n,s)=<(Bn(2*k)=>/(2*k)!)*n**(1-s-2*k)*_p((j)=<s+j,0,2*k-2), _s((j)=<j**(-s),1,n-1)+n**(-s)/2+n**(1-s)/(s-1)+_s((k)=<Tkn(k,n,s)=>,1,m) ]; zeta_Euler_Maclaurin_table(s,n,m)=<last[ table_Bn={1/1,-1/2,1/6,,-1/30,,1/42,,-1/30,,5/66,,-691/2730,,7/6,, -3617/510,,43867/798,,-174611/330,,854513/138,,-236364091/2730,,8553103/6,,-23749461029/870}, table=table_Bn/linspace(0,28,29).!, Tkn(k,n,s)=<table[2*k]*n**(1-s-2*k)*_p((j)=<s+j,0,2*k-2), _s((j)=<j**(-s),1,n-1)+n**(-s)/2+n**(1-s)/(s-1)+_s((k)=<Tkn(k,n,s)=>,1,m) ]; s=1/2+14.135i; n0=max(20,round(abs(s-1/2))); zeta_Euler_Maclaurin(s,n0,4)=>; zeta_Euler_Maclaurin_table(s,n0,14)=>; |
|
目次
Seki-Aitken |
単独scope||式変数への式読出し||再帰call||無名call参照
clear; tn_(=<sn_,n)=<sn_(n)=>-(sn_(n+1)=>-sn_(n)=>)**2/(sn_(n+2)=>-2*sn_(n+1)=>+sn_(n)=>); $tn(=<sn,n)=<last[,tn_(=<sn,n)==>]; sn(n)=<last[ r=1, calc_len_circumcircle(n,r)=<[t=(2*pi/n)/2,x=r*sin(t),len=2*x*n,=<len]=>, calc_len_circumcircle(2**n,r)=>/(2*r) /*sin(pi/2**n)*2**n*/ ]; delta_squared_process(=<sn,nmax)=<[ arr_sn=[arr_sn=[],_s((n)=<arr_sn.push(sn(n)=>),,nmax),=<arr_sn]=>, step(arr)=<[arr_tn=[],len=sizec(arr),_s((n)=<arr_tn.push(tn((n)=<arr[][n],n)=>),,len-3),=<arr_tn]=>, _r(=<arr[sizer(arr)].push(step(=<arr[sizer(arr)-1])=>),arr=arr_sn,floor(nmax/2)), =<arr]=>; make_tn_nested(nmax_)=<[ step=(=<f)=<[=<(n)=<tn(=<f,n)=>]=>f, (nmax__)=<(_r(=<step(=<f)=>,f(n)=<sn(n)=>,floor(nmax__/2)),=<f)=> ](nmax_)=>; nmax=8; delta_squared_process(=<sn,nmax)=>; (make_tn_nested(nmax)=>)(0)=>/*exponential-time*/; pi; |
|
目次
primes |
clear;
isPrime(n)=<[isPrime=n>1,kmax=sqrt(n), _r((k)=<k+1,2,isPrime&&1e6,=<{k>kmax|||n%k==0&&&(isPrime=0)}), =<isPrime]=>; listup_primes(n0,n1)=<[arr=[], _s((n)=<isPrime(n)=>&&&arr.push(n),n0,n1), =<arr]=>; pickup_prime(n,primes)=<[ _r((k)=<last{prime=primes[k],k+1},N=sizer(primes),N,=<{n%prime==0}), =<prime]=>; factorize(n,primes)=<[arr=[], _r((k)=<last{prime=pickup_prime(n,=<primes)=>, arr.push(prime),n=n/prime},isPrime=n>1,isPrime&&1e6,=<{n<=1}), =<arr]=>; [n=100,primes=listup_primes(0,n)=>, primes_factorized=factorize(n,=<trans(primes))=>, =<(n,=prod(primes_factorized):primes_factorized:primes)]=>; |
|
目次
Pythagoras |
clear;
Pythagoras(l,m)=<[=<(m^2-l^2,2*m*l,m^2+l^2)]=>; Pythagoras(2,3)=>; |
|
目次
Fermat |
clear;
Fermat(n,z)=<[ yns=zeros(z,1), zn(z)=<z**n, yn(z,x)=<zn(z)=>-zn(x)=>, _s((x)=<yns[x]=yn(z,x)=>,0,z-1), =<yns]=>; Fermat(2,5)=>; |
|
目次
magic-square |
clear;
get_Mij(m,n,k,sw)=<last[ a0=(m+(n-1)*2)%N, b0=(m+n+(N+k*2-1)/2)%N, ($a,$b)=sw&&&(a0,b0)|||(b0,a0), N*a+b+1]; make_M(N,k,sw)=<zeros(N).map((x,i_,j_)=<get_Mij(i_+1,j_+1,k,sw)=>); N=9; N=floor(N/2)*2+1; ($sw0,$sw1)=[(useRand)=<(useRand&&rand(),useRand&&rand())](false)=>; M=make_M(N,floor(sw0*N),sw1)=>; M.filter((x)=<x==1||x==N**2); sum(M),sum(M.),sum((M[0][0][0].)); |
|
目次
plot2d _EIS |
0D-cell EIS simulation参照
clear; make_IV(dT,dI,f,Nt,Nint,isImplicit)=<last{ $TK=273.15, Tref=15+TK, T=Tref+dT, ($Eact_R0,$Eact_a1,$Eact_a2)=(20,50,10)*1e3, $Rgas=8.31446261815324, ratio_factor(T,Tref,Eact)=<exp((1/Tref-1/T)*Eact/Rgas), ratio_R0=ratio_factor(T,Tref,Eact_R0)=>, ratio_a1=ratio_factor(T,Tref,Eact_a1)=>, ratio_a2=ratio_factor(T,Tref,Eact_a2)=>, L=1e-4, R0=0.5+0.5/ratio_R0, R1=2,C1=0.1, a1=1/(R1*C1),b1=1/C1, a2=0.01,b2=0.12, a1=a1*ratio_a1, a2=a2*ratio_a2, omega=2*pi*f, dt=1/(f*Nt), N=Nt*Nint, tI=zeros(N+1,1),tV=zeros(N+1,1), oldV1=0, oldV2=0, _s((n)=<last{ t=n*dt, It=dI*sin(omega*t), dIt=dI*cos(omega*t)*omega, newV1=switch(isImplicit,(oldV1+b1*dt*It)/(1+a1*dt):1,(1-a1*dt)*oldV1+b1*dt*It), newV2=switch(isImplicit,(oldV2+b2*dt*It)/(1+a2*dt):1,(1-a2*dt)*oldV2+b2*dt*It), oldV1=newV1, oldV2=newV2, Vt=L*dIt+R0*It+newV1+newV2, tI[n]=It, tV[n]=Vt },0,N) }; FT_IV(IV,f,dt)=<[ out=<zIV,
init=<last{N=sizer(IV)},
run=<last{
init=>,run=>,return=out=>,
omega=2*pi*f, calc_w(n)=<switch((n==0)|(n==N-1),1:n%2==0,2:1,4), calc_v(n,t,val)=<calc_w(n)=>*val*exp(-i*omega*t), zIV=_s((n)=<calc_v(n,n*dt,IV[n])=>,0,N-1)*dt/3 }, =<return]=>; calc_Z(zI,zV)=<[ out=<Z,
init=<last{0},
run=<last{
init=>,run=>,return=out=>,
Z=zV/zI }, =<return]=>; sweep_f(dT,dI,f0,f1,Nf,Nt,Nint,isImplicit)=<[ out=<fZ,
init=<last{fZ=zeros(Nf+1,2)},
run=<last{
init=>,run=>,return=out=>,
calc_f(n)=<exp(log(f0)+(log(f1)-log(f0))*n/Nf), _s((n)=<last{ f=calc_f(n)=>, make_IV(dT,dI,f,Nt,Nint,isImplicit)==>, fZ[n]=(f,calc_Z(FT_IV(=<tI,f,dt)=>,FT_IV(=<tV,f,dt)=>)=>) },0,Nf) }, =<return]=>; plot2d_EIS(isBode,fZ)=<[ out=<(xt,yt), scope2storage=<last{add__(xt),add__(yt)},
init=<last{N=sizer(fZ),xt=zeros(N,1),yt=zeros(N,1)},
run=<last{
init=>,run=>,return=out=>,scope2storage=>,
switch( isBode==0/*Nyquist-plot(real(Z),-imag(Z))*/, =<_s((n)=<last{ Z=fZ[n][1], xt[n]=real(Z), yt[n]=-imag(Z) },0,N-1): isBode>0/*Bode-plot(log10(f),|Z|)*/, =<_s((n)=<last{ f=fZ[n][0], Z=fZ[n][1], xt[n]=log10(f), yt[n]=abs(Z) },0,N-1): 1/*else-Bode-plot(log10(f),deg_phi)*/, =<_s((n)=<last{ f=fZ[n][0], Z=fZ[n][1], xt[n]=log10(f), yt[n]=deg_atan2(imag(Z),real(Z)) },0,N-1) ) }, =<return]=>; [isImplicit=1,isBode=0, =<plot2d_EIS(isBode,=<sweep_f(0,1e-3,1e3,0.01,10,100,1,isImplicit)=>)=>]=>; |
|
目次
plot2d _EIS_DFT |
0D-cell EIS simulation参照
clear; make_IV(dT,dI,f,Nt,Nint,isImplicit)=<last{ $TK=273.15, Tref=15+TK, T=Tref+dT, ($Eact_R0,$Eact_a1,$Eact_a2)=(20,50,10)*1e3, $Rgas=8.31446261815324, ratio_factor(T,Tref,Eact)=<exp((1/Tref-1/T)*Eact/Rgas), ratio_R0=ratio_factor(T,Tref,Eact_R0)=>, ratio_a1=ratio_factor(T,Tref,Eact_a1)=>, ratio_a2=ratio_factor(T,Tref,Eact_a2)=>, L=1e-4, R0=0.5+0.5/ratio_R0, R1=2,C1=0.1, a1=1/(R1*C1),b1=1/C1, a2=0.01,b2=0.12, a1=a1*ratio_a1, a2=a2*ratio_a2, omega=2*pi*f, dt=1/(f*Nt), N=Nt*Nint, tI=zeros(N+1,1),tV=zeros(N+1,1), oldV1=0, oldV2=0, _s((n)=<last{ t=n*dt, It=dI*sin(omega*t), dIt=dI*cos(omega*t)*omega, newV1=switch(isImplicit,(oldV1+b1*dt*It)/(1+a1*dt):1,(1-a1*dt)*oldV1+b1*dt*It), newV2=switch(isImplicit,(oldV2+b2*dt*It)/(1+a2*dt):1,(1-a2*dt)*oldV2+b2*dt*It), oldV1=newV1, oldV2=newV2, Vt=L*dIt+R0*It+newV1+newV2, tI[n]=It, tV[n]=Vt },0,N) }; DFT_IV(IV,f,dt)=<[ out=<zIV,
init=<last{N=sizer(IV)},
run=<last{
init=>,run=>,return=out=>,
omega=2*pi*f, zIV=_s((n)=<IV[n]*exp(-i*omega*n*dt),0,N-1)/*(f*dt)=1/Nt*/ }, =<return]=>; calc_Z(zI,zV)=<[ out=<Z,
init=<last{0},
run=<last{
init=>,run=>,return=out=>,
Z=zV/zI }, =<return]=>; sweep_f(dT,dI,f0,f1,Nf,Nt,Nint,isImplicit)=<[ out=<fZ,
init=<last{fZ=zeros(Nf+1,2)},
run=<last{
init=>,run=>,return=out=>,
calc_f(n)=<exp(log(f0)+(log(f1)-log(f0))*n/Nf), _s((n)=<last{ f=calc_f(n)=>, make_IV(dT,dI,f,Nt,Nint,isImplicit)==>, fZ[n]=(f,calc_Z(DFT_IV(=<tI,f,dt)=>,DFT_IV(=<tV,f,dt)=>)=>) },0,Nf) }, =<return]=>; plot2d_EIS_DFT(isBode,fZ)=<[ out=<(xt,yt), scope2storage=<last{add__(xt),add__(yt)},
init=<last{N=sizer(fZ),xt=zeros(N,1),yt=zeros(N,1)},
run=<last{
init=>,run=>,return=out=>,scope2storage=>,
switch( isBode==0/*Nyquist-plot(real(Z),-imag(Z))*/, =<_s((n)=<last{ Z=fZ[n][1], xt[n]=real(Z), yt[n]=-imag(Z) },0,N-1): isBode>0/*Bode-plot(log10(f),|Z|)*/, =<_s((n)=<last{ f=fZ[n][0], Z=fZ[n][1], xt[n]=log10(f), yt[n]=abs(Z) },0,N-1): 1/*else-Bode-plot(log10(f),deg_phi)*/, =<_s((n)=<last{ f=fZ[n][0], Z=fZ[n][1], xt[n]=log10(f), yt[n]=deg_atan2(imag(Z),real(Z)) },0,N-1) ) }, =<return]=>; [isImplicit=1,isBode=0, =<plot2d_EIS_DFT(isBode,=<sweep_f(0,1e-3,1e3,0.01,10,100,1,isImplicit)=>)=>]=>; |
|
目次
plot2d _IV |
0D-cell EIS simulation参照
clear; make_tIV(dT,dI,f,Nt,Nint,isImplicit)=<last{ $TK=273.15, Tref=15+TK, T=Tref+dT, ($Eact_R0,$Eact_a1,$Eact_a2)=(20,50,10)*1e3, $Rgas=8.31446261815324, ratio_factor(T,Tref,Eact)=<exp((1/Tref-1/T)*Eact/Rgas), ratio_R0=ratio_factor(T,Tref,Eact_R0)=>, ratio_a1=ratio_factor(T,Tref,Eact_a1)=>, ratio_a2=ratio_factor(T,Tref,Eact_a2)=>, L=1e-4, R0=0.5+0.5/ratio_R0, R1=2,C1=0.1, a1=1/(R1*C1),b1=1/C1, a2=0.01,b2=0.12, a1=a1*ratio_a1, a2=a2*ratio_a2, omega=2*pi*f, dt=1/(f*Nt), N=Nt*Nint, tt=zeros(N+1,1),tI=zeros(N+1,1),tV=zeros(N+1,1), oldV1=0, oldV2=0, _s((n)=<last{ t=n*dt, It=dI*sin(omega*t), dIt=dI*cos(omega*t)*omega, newV1=switch(isImplicit,(oldV1+b1*dt*It)/(1+a1*dt):1,(1-a1*dt)*oldV1+b1*dt*It), newV2=switch(isImplicit,(oldV2+b2*dt*It)/(1+a2*dt):1,(1-a2*dt)*oldV2+b2*dt*It), oldV1=newV1, oldV2=newV2, Vt=L*dIt+R0*It+newV1+newV2, tt[n]=t, tI[n]=It, tV[n]=Vt },0,N) }; plot2d_IV(dT,dI,f,Nt,Nint,isImplicit)=<[ out=<(xt,yt), scope2storage=<last{add__(xt),add__(yt)},
init=<last{N=Nt*Nint,xt=zeros(N+1,1),yt=zeros(N+1,2)},
run=<last{
init=>,run=>,return=out=>,scope2storage=>,
make_tIV(dT,dI,f,Nt,Nint,isImplicit)==>, _s((n)=<last{xt[n]=tt[n],yt[n]=(tI[n],tV[n])},0,N) }, =<return]=>; [isImplicit=1, =<plot2d_IV(0,1e-3,0.5,100,2,isImplicit)=>]=>; |
|
目次
heat0d _evolution |
0D-heat simulation参照
clear; heat0d_evolution(t,dt,kalpha0,kalpha1,kalbedo,kabsorb)=<[ out=<{t_total,dT}, scope2storage=<last{add__(oldT),add__(t_total)},
init=<last{
I0=1367, sigma=5.670374419184429e-8, TK=273.15, T0=15, T1=-56.5, T0K=T0+TK, T1K=T1+TK, H1=11000, R0=6378136.6, R1=R0+H1, S0=pi*R0^2, S1=pi*R1^2, A0=S0*4, A1=S1*4, albedo0=0.3, e0=1, TeK=(I0*(1-albedo0)/(4*e0*sigma))**0.25, Te=TeK-TK, W0=S1*I0, Wee=A0*(e0*sigma*TeK**4), We0=A0*(e0*sigma*T0K**4), absorbh=1-W0*(1-albedo0)/We0, absorbhmax=0.5, absorb0=We0*absorbh/(W0*(1-albedo0)), absorb0max=We0*absorbhmax/(W0*(1-albedo0)), kh0=(absorbhmax-absorbh)/(absorb0max-absorb0), Te_th(a)=<(I0*(1-albedo0)/(2*(2-a)*e0*sigma))**0.25-TK, Te_th0=Te_th(absorbh*2)=>, Wea=We0*absorbh, Wet=We0*(1-absorbh), l=0.0241, rho=1.29, cp=1007, V=_i((r)=<4*pi*r^2,R0,R0+H1), C=rho*cp*V, alpha10=-W0*(1-albedo0)*absorb0/(A1*(T1-T0)), alpha0=alpha10*kalpha0, alpha1=alpha10*kalpha1, albedo=albedo0*kalbedo, absorb=absorb0*kabsorb, absorbe=(1-albedo)*absorb, T=T0, flux0=alpha0*(T0-T), flux1=alpha1*(T1-T), W2=flux0*A0, W1=flux1*A1, W0a=W0*albedo, W0t=W0*(1-albedo)*(1-absorb), W0e=W0*(1-albedo)*absorb, (Wee-Wet), (Wea-W0e), (W0t+W0e-Wet), (W0a+W0t+W0e-W0), (W1+W0e+W2), a=(alpha1*A1+alpha0*A0)/C, b=(alpha1*A1*T1+W0*(1-albedo)*absorb+alpha0*A0*T0)/C, switch(has__(t_total)==0,=<last{t_total=0,oldT=T0}), newT=oldT },
run=<last{
init=>,run=>,return=out=>,scope2storage=>,
step=<last{newT=(oldT+b*dt)/(1+a*dt),oldT=newT}, evolution=<_r((n)=<step=>,N=round(t/dt),N), evolution=>, dT=newT-T0, t_total=t_total+N*dt }, =<return]=>; [cond_error=(has__(t_total)==0)&&has__(oldT), proc=<[s_1day=60*60*24, =<heat0d_evolution(s_1day*30,s_1day,0,0.98,1,1)=>]=>, =<switch(cond_error==0,=<proc:1,-999/*error-code*/)]=>; |
|
目次
heat1d _evolution |
clear;
heat1d_evolution(t,dt,kalpha0,kalpha1,kalbedo,kabsorb,N)=<[ out=<{t_total,newT}, scope2storage=<last{add__(oldT),add__(t_total)},
init=<last{
I0=1367, sigma=5.670374419184429e-8, TK=273.15, T0=15, T1=-56.5, T0K=T0+TK, T1K=T1+TK, H1=11000, R0=6378136.6, R1=R0+H1, S0=pi*R0^2, S1=pi*R1^2, A0=S0*4, A1=S1*4, albedo0=0.3, e0=1, TeK=(I0*(1-albedo0)/(4*e0*sigma))**0.25, Te=TeK-TK, W0=S1*I0, Wee=A0*(e0*sigma*TeK**4), We0=A0*(e0*sigma*T0K**4), absorbh=1-W0*(1-albedo0)/We0, absorbhmax=0.5, absorb0=We0*absorbh/(W0*(1-albedo0)), absorb0max=We0*absorbhmax/(W0*(1-albedo0)), kh0=(absorbhmax-absorbh)/(absorb0max-absorb0), Te_th(a)=<(I0*(1-albedo0)/(2*(2-a)*e0*sigma))**0.25-TK, Te_th0=Te_th(absorbh*2)=>, Wea=We0*absorbh, Wet=We0*(1-absorbh), l=0.0241, rho=1.29, cp=1007, V=A1*H1, C=rho*cp*V, alpha10=-W0*(1-albedo0)*absorb0/(A1*(T1-T0)), alpha0=alpha10*kalpha0, alpha1=alpha10*kalpha1, albedo=albedo0*kalbedo, absorb=absorb0*kabsorb, absorbe=(1-albedo)*absorb, T=T0, flux0=alpha0*(T0-T), flux1=alpha1*(T1-T), W2=flux0*A0, W1=flux1*A1, W0a=W0*albedo, W0t=W0*(1-albedo)*(1-absorb), W0e=W0*(1-albedo)*absorb, (Wee-Wet), (Wea-W0e), (W0t+W0e-Wet), (W0a+W0t+W0e-W0), (W1+W0e+W2), dC=C/N, a0=alpha0*A1/dC, a1=alpha1*A1/dC, b=0, c=W0*(1-albedo)*absorb/C+a0*T0, d=alpha1*A1*(T1-T0)/C, A=zeros(N,N), A[-1][0][1]=(-a1*dt,1+2*a1*dt,-a1*dt), A[0][0]=1+a1*dt+a0*dt, A[-1][-1]=1+a1*dt, switch(has__(t_total)==0,=<last{t_total=0,oldT=zeros(N,1)+Te}), newT=oldT },
run=<last{
init=>,run=>,return=out=>,scope2storage=>,
step=<last{ r=oldT+b*dt, r[0]=r[0]+c*dt, r[-1]=r[-1]+d*dt, oldT=Newton(=<A*__x__=r,=<{oldT}) }, evolution=<_r((n)=<step=>,N=round(t/dt),N), evolution=>, newT=oldT, dT=newT-T0, t_total=t_total+N*dt }, =<return]=>; [cond_error=(has__(t_total)==0)&&has__(oldT), proc=<[s_1day=60*60*24, =<heat1d_evolution(s_1day*30,s_1day,0,1,1,1,20)=>]=>, =<switch(cond_error==0,=<proc:1,-999/*error-code*/)]=>; |